高速铁路轮轨滚动噪声预测计算模型研究

步青松

（中国铁道科学研究院集团有限公司节能环保劳卫研究所，北京 100081）

高速铁路产生的噪声问题影响乘客舒适性和沿线声环境［1］，成为影响铁路绿色环保、可持续发展以及高速铁路“走出去”的关键因素之一。国内外针对高速铁路噪声源开展的大量研究表明，高速铁路是一种呈现多源特征的宽频噪声源，其中轮轨噪声是铁路从低速向高速发展过程中始终存在的重要噪声源［2-4］。现有研究对高速铁路轮轨噪声的预测计算仍存在不足，其主要原因在于：①缺乏准确的高速轮轨噪声激励输入；②针对轮轨噪声随运行速度的变化规律均为普速铁路研究成果，对高速铁路的适用性有待验证；③高速铁路轮轨区域同时存在较大的气动噪声和轮轨噪声，影响机制复杂，开展高速轮轨噪声预测研究缺乏有效验证；④声源过度简化，通常将车轮视为点声源、钢轨视为线声源。

为了进一步研究轮轨噪声特性，本文基于我国高速铁路噪声源定量化识别分析结果，对高速铁路噪声源特性进行分析，并通过1∶1 轮轨滚动试验台研究纯轮轨激励条件下动车组运行速度v由100 km/h 提高至350 km/h 的轮轨滚动噪声源变化特性；基于轮轨声辐射和轮轨振动响应特征，构建符合轮轨噪声辐射和指向特性的轮对和钢轨的噪声预测计算模型。

1 高速铁路噪声源识别

基于声阵列技术［5-6］，以复兴号动车组为研究对象，开展高速铁路噪声源定量化识别分析，如图1 所示，典型车速下的识别结果见图2。

图1 高速铁路噪声源识别现场

识别结果表明：①v≤200 km/h 时，主要噪声源为轮轨区域，受电弓区域等气动噪声源声级水平较低但增幅显著；轮轨区域声功率与v2成正比。②v＞200 km/h时，主要噪声源仍分布在轮轨区域，但受电弓、头车排障器等区域的气动噪声增幅显著；v达到300 km/h 后，受电弓区域成为声级最高的噪声源，但由于其发声面积小，对噪声总贡献仍低于轮轨区域；v超过350 km/h后，转向架区域气动噪声成为最主要噪声源之一。各区域噪声声功率随车速的变化不同，受电弓区域与v6成正比，车体区域与v4～v5成正比，轮轨区域与v4成正比。动车组各区域均存在较大的气动噪声，轮轨区域为总声功率最高的噪声源。

采用声阵列技术仅能识别不同区域噪声源，不能区分同一区域不同机理产生的噪声源。为明确轮轨区域噪声的构成，对轮轨滚动噪声的变化特征展开深入研究。

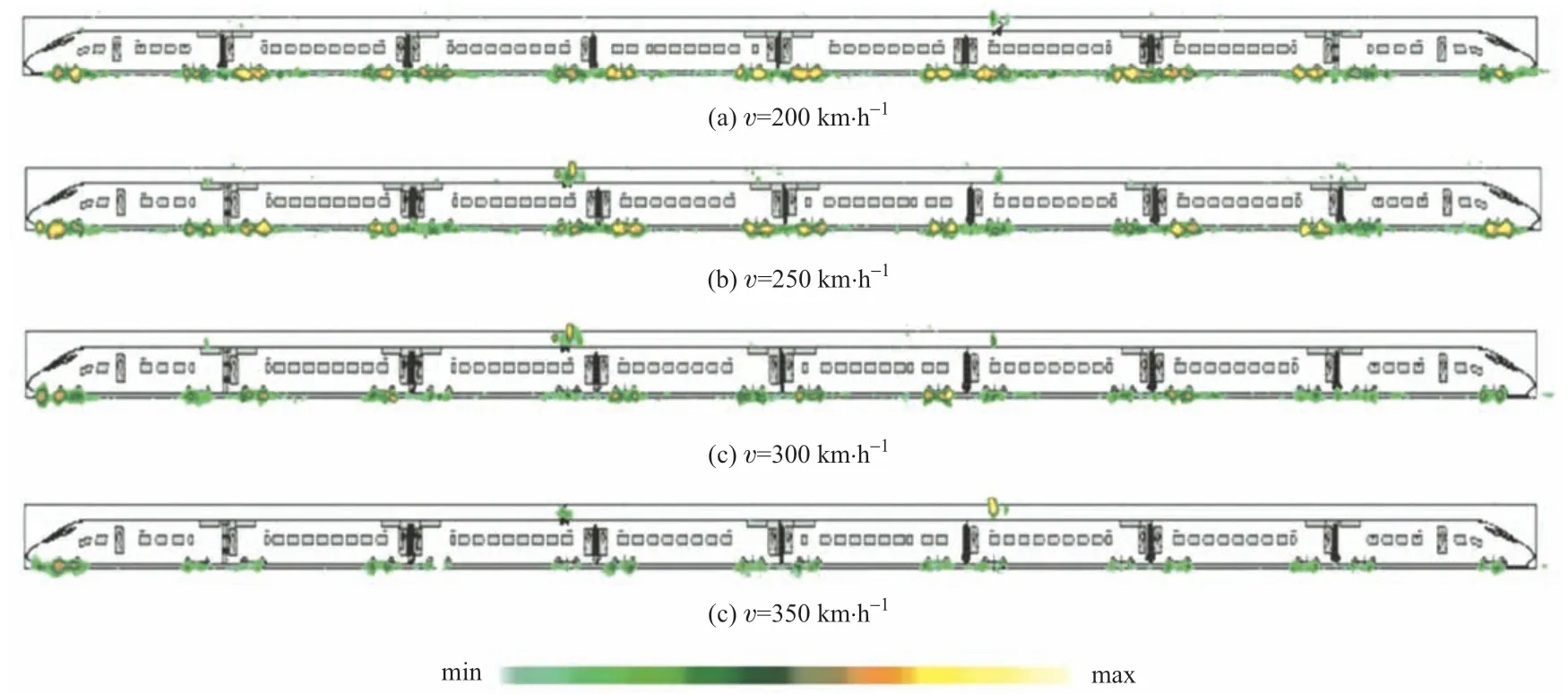
图2 典型车速下高速铁路噪声源识别结果

2 全尺寸轮轨滚动噪声试验

基于大同—西安客运专线轨道不平顺参数，通过1∶1高速轮轨滚动试验台，选用复兴号动车组拖车车轮、轴承、轴等一系悬挂部件，模拟其从100 km/h 提速至350 km/h 的轮轨滚动噪声变化特性（图3）。测点布置见图4，其中C1—C4 为轮轨接触测点。不同速度下轮轨接触处噪声试验结果见图5。

图3 高速轮轨滚动试验现场

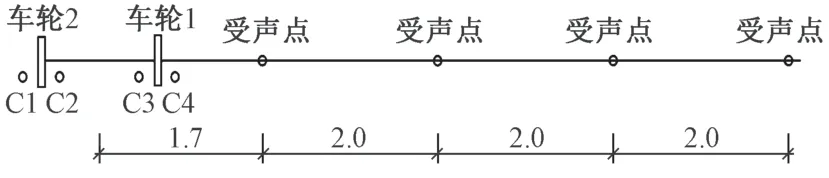
图4 高速轮轨滚动试验测点布置（单位：m）

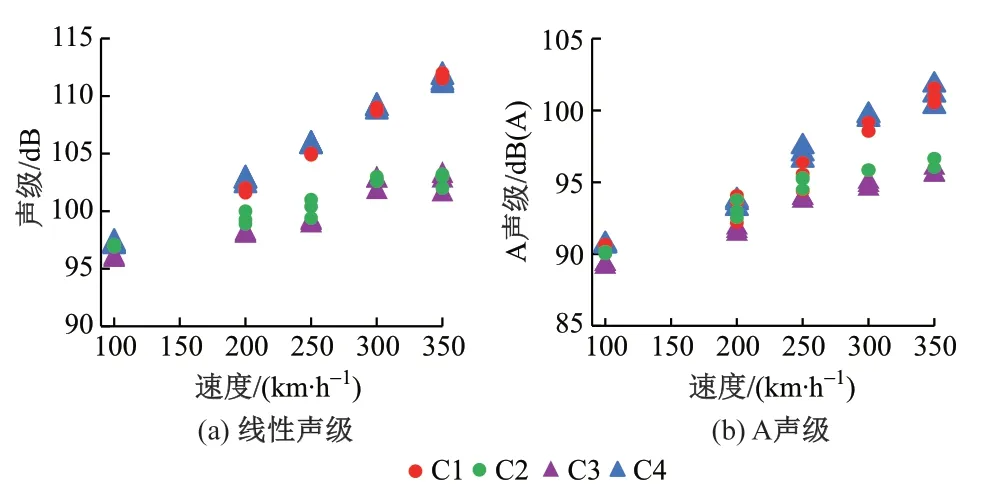
图5 不同速度下轮轨接触处噪声试验结果

由图5 可见：①模拟直线运行时两轮噪声基本一致。②车轮内侧测点的噪声低于外侧；随着运行速度提高，内外侧测点的差异逐渐加大，内侧测点噪声随速度变化明显低于外侧。这是因为两轮间距较小，来自相同的激励源，为相干声源，在两轮间产生了明显的干涉效应。这也证明了轮轨噪声源模型不能简单采用点声源或线声源来表征。③A 声级处理后，车轮内外侧测点的声级差异有所减小。

根据图5（b），拟合车轮外侧噪声A 声级随运行速度的变化曲线，见图6。

图6 轮轨噪声A声级随速度变化的拟合曲线

轮轨噪声A 声级随受声点到轮轴中心距离变化的实测曲线及拟合曲线见图7。

图7 轮轨噪声A声级随距离变化规律

由图6、图7 可见：轮轨噪声A 声级随运行速度呈18lg～20lg 变化，与既有结论中轮轨噪声与v2～v3成正比基本一致；轮轨噪声A 声级随距离变化呈12.4lg 的衰减，与传统点声源、线声源的衰减规律并不一致。

3 轮轨滚动噪声辐射预测模型

为解决目前轮轨噪声预测计算中声源被过度简化的问题，基于轮轨激励发声特征，构建满足实际车辆和轨道条件的多轮对、长钢轨噪声计算模型。

3.1 车轮辐射噪声计算

高速铁路噪声预测和评价主要关注列车通过等效声级，本文重点关注列车通过期间轮轨噪声对受声点的影响。噪声叠加时考虑两轮产生的干涉作用。

以列车中部车轮为例，车轮与受声点的相对位置如图8所示。设动车组车长为L，其中心点O正对受声点S，d为受声点S到线路中心线的水平距离。以O为原点，x沿线路中心线水平向右为正，则动车组运行时中部车轮的运行轨迹可视为［-L/2，L/2］。r为轮轴中心A到受声点S的距离；θ为SA与SO的夹角；轨距d0=1 435 mm。

图8 车轮与受声点的相对位置

基于自由场条件下的声学波动方程，车轮1、车轮2在受声点产生的声压Pw1(t)，Pw2(t)分别为

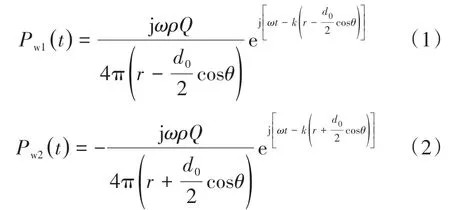
式中：t为时间；ω为圆频率，ω =2πf，其中f为声波频率；ρ为空气密度；Q为声源体积速度；k为波数，k=2π/λ，其中λ为声波波长。

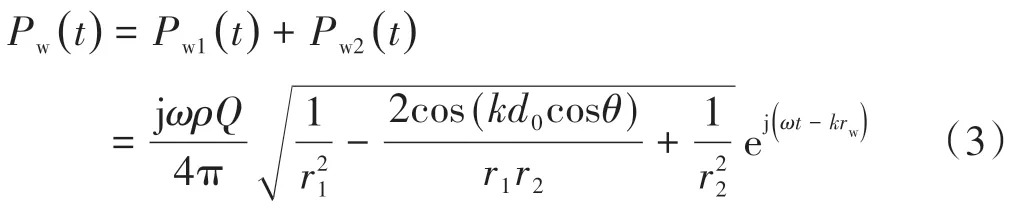
式中，rw为两轮对产生的总声压对应的相位参数。

根据运动方程，质点振动速度uw(t)的表达式为

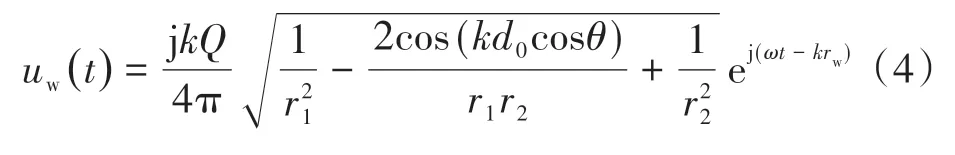
可得出受声点处的总声强I为

式中，T为声波周期，T= 1/f= 2π/ω。

考虑到实际应用时r≫d0，式（5）可简化为

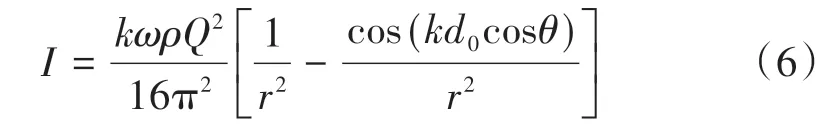
轮对辐射声功率W为

式中：φ为极角；a为球声源半径为车轮振动速度平方均值。

由于计算列车通过等效声级时仅关注动车组车头通过受声点至车尾通过受声点这段时间，因此忽略多普勒频移影响。此外，轮轨支撑于轨道上方，更符合半自由场传播条件。

动车组运行过程中，中部车轮轮对在受声点产生的平均声压贡献为

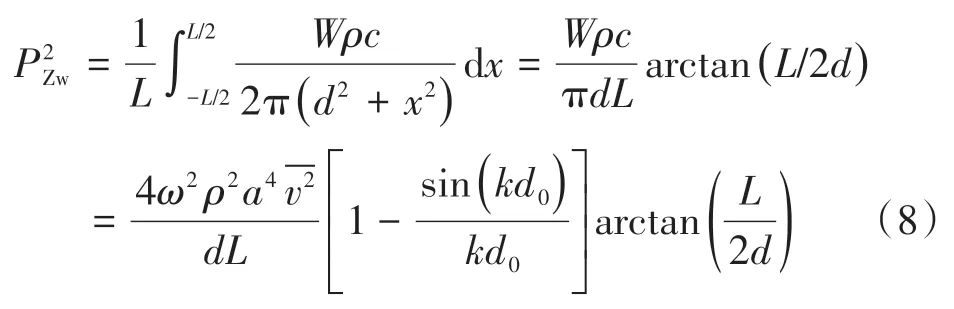
式中，c为声波速度。

动车组其他轮对与中部车轮的声压贡献计算方法一致。

假定转向架均位于车厢端部，Lt为单节车厢长度。i表示从车头算起的第i个转向架。整列动车组各轮对在受声点的平均声压贡献为

动车组运行过程中，轮对产生的总噪声影响为所有轮对在受声点产生的总平均声压贡献

式中，n为整列动车组轮对总数。

3.2 钢轨辐射噪声计算

由于动车组运行过程中钢轨纵向各点振动较为平稳，本文将列车通过时单根钢轨振动视为有限点声源组成，考虑2根钢轨声源相干特性，各点声源在受声点的噪声影响可以叠加。

在2根钢轨长度方向各取一段dx。自由场条件下钢轨1、钢轨2 的dx段在受声点的噪声影响PR1(t)，PR2(t)分别为

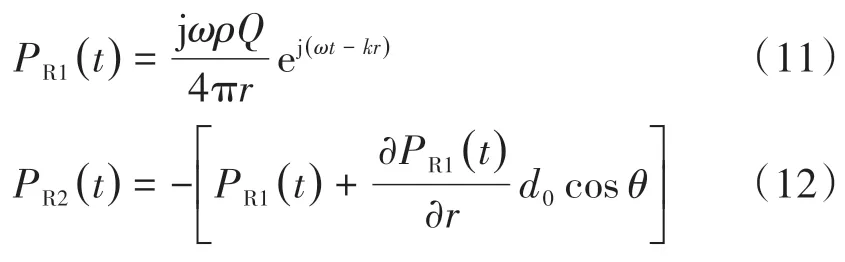
合成总声压为

质点振动速度uR(t)的表达式为

可得dx在受声点产生的总声强Ix为

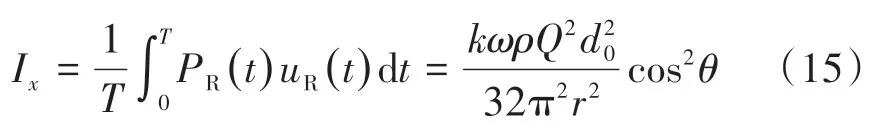
半自由场条件下动车组运行过程中钢轨振动在受声点产生的总声压级为

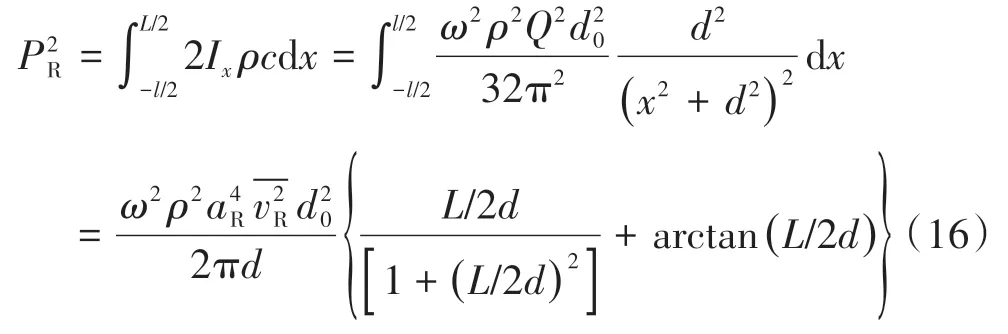
式中：aR为钢轨上点声源有效辐射半径，本文取钢轨高度为钢轨振动速度平方均值。

3.3 轮轨辐射总噪声

列车通过时段内，轮轨辐射总平均声压级P2为

3.4 模型验证

为验证预测模型的精度，在大西客运专线开展了车地同步试验，对复兴号动车组轮对轴箱、钢轨等部位振动响应以及同区段噪声进行测试。车轮轴箱振动响应见图9，钢轨振动响应见图10。

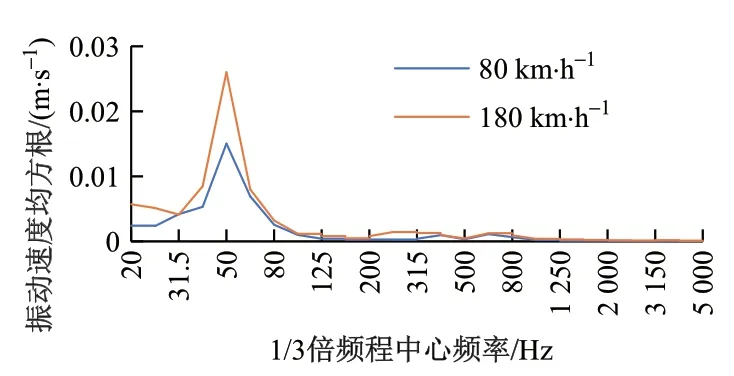
图9 复兴号动车组车轮轴箱振动响应

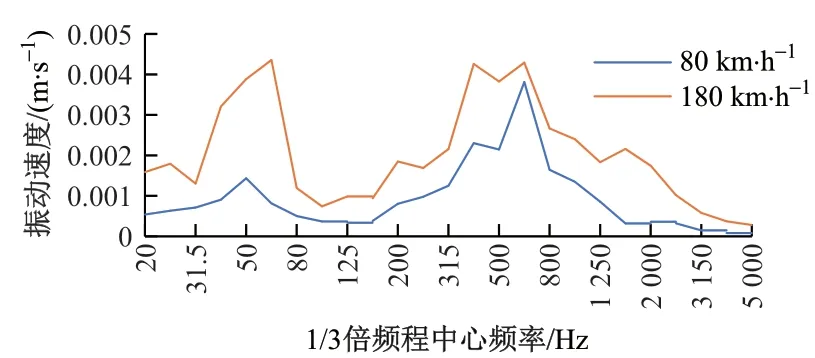
图10 复兴号动车组通过时钢轨振动响应

将复兴号动车组分别以80，180 km/h 的速度通过时的轮轨振动响应作为输入条件，预测与线路中心线距离15 m 且与轨面等高位置的列车通过噪声，并与现场实测值对比，见图11。

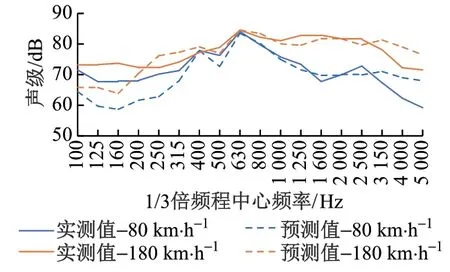
图11 模型预测值与现场实测值对比

由图11可见，在关键频带，噪声峰值频带幅值、中心频率的模型预测值与现场实测值非常吻合，在200 Hz及以下低频区域和3 000 Hz 以上的高频区域有差异。低频差异主要是由于实测噪声是动车组通过时的综合噪声，包括列车通过噪声和环境噪声，低频声辐射效率较高的轨道结构和桥梁结构噪声对低频噪声贡献较大。高频噪声差异主要是由于除声源传播距离引起的衰减外，传播过程中空气吸收对高频衰减作用较大，而本次预测模型主要考虑轮轨噪声辐射噪声，空气吸收已经在我国铁路整车噪声预测模型中予以考虑。

对于与线路中心线距离15 m 且与轨面等高的位置，列车以80 km/h 通过时等效连续A 声级的预测值和实测值分别为85.7，86.1 dB（A）；以180 km/h 通过时的预测值和实测值分别为91.5，91.8 dB（A）。可见，实测值高于预测值0.5 dB（A）以内，预测精度满足要求，验证了我国高速铁路噪声源识别分析提出的主要结论，即动车组以200 km/h 以下速度运行时，轮轨噪声是最主要的噪声源。

4 结论

1）动车组运行速度低于200 km/h 时，主要噪声源为轮轨噪声，受电弓等气动噪声源声级水平较低但增幅显著；车速高于300 km/h 时，受电弓成为声级最高的噪声源，但对噪声总贡献仍低于轮轨区域噪声；车速高于350 km/h 时，气动噪声成为最主要噪声源之一。

2）轮轨滚动试验表明：直线工况运行时，左右轮噪声基本一致；轮对属于明显的相干声源，不能采用点声源模拟；轮轨噪声A 声级随运行速度呈18lg～20lg变化，随距离呈12.4lg 衰减变化，属于较为复杂的噪声源衰减特性。

3）基于2 车轮及2 根钢轨之间的声波干涉叠加，构建了表征多轮对运行轨迹和钢轨共同作用下轮轨振动响应声辐射数值计算模型。现场对比分析表明：复兴号动车组分别以80，180 km/h 通过时，模型预测值与现场实测值在关键频带完全吻合，其中列车通过等效连续A 声级实测值与预测值之差小于0.5 dB（A），预测精度较高。