高速磁浮大型箱梁日照温度效应分析

黄全成,滕念管

(上海交通大学船舶海洋与建筑工程学院,上海 200240)

引言

当前我国正在研究时速600 km以上的高速磁浮列车及其轨道梁，传统的磁浮线路通常采用高架线路结构，轨道梁两端搁置在支墩上，列车环抱轨道梁运行，这不利于设备的检修以及人员的逃生。

随着磁浮交通的进一步发展，轨道梁的功能要求越来越高，国内相关单位申请了许多关于梁上梁式轨道梁的相关专利[1-3]，梁上梁式轨道梁上部采用常规轨道梁，下部采用大型箱梁用来支撑上部轨道梁，在磁浮线路中有较好的应用前景，梁上梁式轨道梁示意如图1所示。

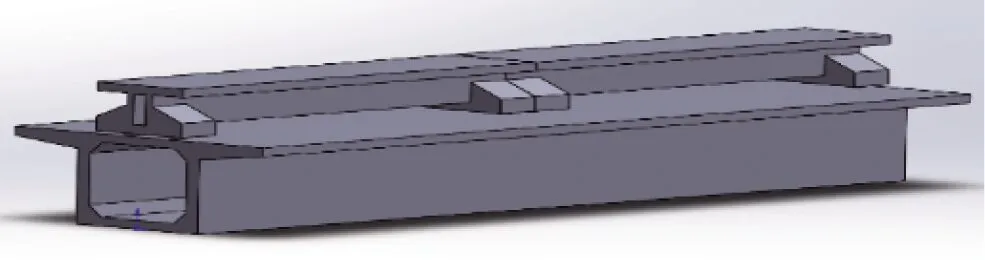
图1 梁上梁式轨道梁示意

国内外学者对混凝土日照温度效应进行了大量研究。李全林(2004)在实测数据的基础上利用有限元软件ANSYS，对混凝土箱梁截面温度场进行了理论分析，并研究了桥梁方位角、翼缘悬臂长度和腹板高度对箱梁温度场和温度应力的影响[4]。李玉磊(2010)研究了上海线磁浮轨道梁在日大气环境下的二维瞬态温度场分布以及不同跨型的轨道梁在温度荷载作用下的挠度变形问题[5]。Tayi等(2015)利用实测数据验证了箱梁三维温度场有限元结果的正确性，研究了混凝土密度、导热系数、比热容、表面发射率和表面吸收率对箱梁温度分布的影响[6]。张誉瀚等(2017)利用ANSYS建立箱梁二维温度场有限元分析模型，并将有限元模拟结果与实测值进行对比，验证了有限元方法的正确性[7]。李岩(2018)建立了中低速磁浮轨道结构有限元模型，分析了在乌鲁木齐地区的温度气候条件下中低速磁浮单箱单室轨道梁的变形和应力特性，并分析了在温度变形作用下的车桥耦合振动[8]。刁飞(2018)利用Python建立了箱梁温度边界条件，在此基础上对斜拉桥进行二维瞬态热分析，得到了箱梁沿梁高与梁宽方向的最不利温差，并将结果与铁路规范对比[9]。邹波(2019)分析了混凝土单箱双室磁浮轨道梁在日大气环境下的温度效应，拟合了竖向与横向温度梯度曲线，并将其与规范进行对比[10]。

综上可知，现有文献对于箱梁温度场的分析多集中于二维热分析，并对竖向与横向温度梯度进行拟合。实际上，在分析箱梁的竖向温度变形时，横向温差会对箱梁产生一定的影响，单独考虑竖向温度梯度不能准确地计算竖向温度变形。对于磁浮系统来说，温度变形要求极其严格，需要明确其温度变形。目前，时速600 km以上高速磁浮轨道技术研究工作是由青岛中车四方车辆有限公司牵头，后续相应的试验线也极有可能在青岛展开，而上海自2003年起高速磁浮就已运行。相比于上部轨道梁，下部承重箱梁在结构上更为重要，上部轨道梁类似于传统轮轨铁路的轨道。因此，针对磁浮下部大型箱梁进行青岛与上海两地的日照温度效应分析，为以后的工程实践提供一定的参考。

1 日大气环境下箱梁与外界的热交换原理

混凝土箱梁一般暴露于大气环境中，在外界环境的影响下混凝土箱梁的温度发生变化。箱梁暴露在大气中工作时与周围环境的热交换主要包括三种：太阳辐射、对流换热以及辐射换热。其中太阳辐射属于第二类边界条件，对流换热与辐射换热属于第三类边界条件[11]。箱梁内部的边界条件包括各表面与箱内空气的对流换热以及各表面之间的辐射换热。

2 有限元方法验证

目前，国内没有用于时速600 km以上高速磁浮大型箱梁，因此难以开展试验研究承重箱梁在日环境下的温度效应。为了验证有限元分析的正确性，本节参考文献[12]，利用ANSYS模拟幸福源水库双线特大桥的温度效应，并将结果与试验数据进行对比。

2.1 桥梁相关参数

由文献[12]可知，桥梁所处地理位置为24.946°N，110.579°E，桥梁所处周围环境为山区。桥梁截面尺寸及测点位置如图2所示。

图2 桥梁截面尺寸及测点位置示意[12](单位：mm)

实测风速为2.5 m/s，混凝土密度为2 500 kg/m3，导热系数与比热容分别为2.5 W/(m·℃)和880 J/(kg·℃)。对于大气温度，文献[12]只有相关图表，没有具体数值，箱梁外部大气温度变化可以取为介于最高气温与最低气温之间的正弦曲线[13]，因此箱梁所处地区气温可近似表示为

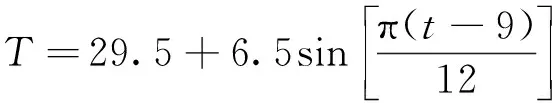
(1)

式中，T为大气温度；t为时间。

2.2 有限元拟合结果与试验结果对比

在将有限元结果与试验数据对比的过程中，由于没有完整的试验数据结果，因此在进行对比分析时只能进行简单的定量分析。

顶板测点11的温度时程曲线如图3所示。由图3可知，有限元结果与试验数据在一天内的变化趋势基本一致，测点11在上午6点到下午2点温度不断升高，在下午2点以后温度降低。有限元模拟结果表明：测点11在一天内的最高温度为48.76 ℃，最低温度为26.98 ℃。试验结果表明：测点11在一天内的最高温度大约为49 ℃，最低温度大约为26 ℃，最高温度与最低温度误差均在5%以内。

图3 测点11温度时程曲线

西腹板测点19的温度时程曲线如图4所示。对比图4(a)、图4(b)可知，测点在一天内的整体温度变化趋势一致。在下午4点到6点时刻，图4(a)中测点的温度急剧升高，该时刻测点19刚由阴影状态过渡到太阳直接辐射状态，与试验结果相比存在一定差别。但是，有限元拟合结果表明，测点19的最高温度为39.1 ℃，最低温度为27.2 ℃；由图4(b)可知，试验测得测点19在一天内的最高温度大约为39 ℃，最低温度大约为25.2 ℃，误差分别为0.26%和7.9%。

图4 测点19温度时程曲线

东腹板测点34的温度时程曲线如图5所示。由图5可以发现，有限元计算结果与试验数据在上午11点到下午4点时间范围内有一些区别。主要表现为有限元结果在该时间段内温度仍然有一个缓慢的增加，而试验数据表明在该时间范围内测点34温度缓慢降低。这主要是由于在有限元模拟过程中，外界气温在该时间范围内仍大于测点34的温度，而实际上外界气温并不能完全用正弦函数拟合，这是由于外界气温设置导致的误差，实际上测点温度在该时段内的误差并不是很大。

图5 测点34温度时程曲线

底板测点18的温度时程曲线如图6所示。由图6(a)可知，测点18在一天内的最高温度为35.25 ℃，最低温度为27.53 ℃；由图6(b)可知，试验测得测点18在一天内的最高温度为33.8 ℃，最低温度大约为25.2 ℃，误差分别为4.3%和9.2%，最低温度误差较大，其主要是由于初始温度场设置的影响。

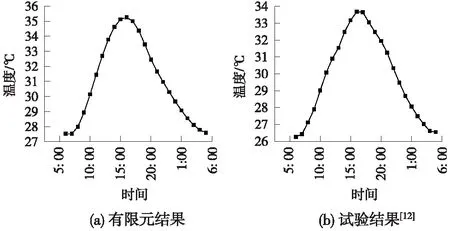
图6 测点18温度时程曲线

由以上分析可知，部分节点的误差大于5%。产生误差的原因有很多，具体包括模型材料参数与实际参数不完全相符，试验过程中测点位置不完全正确，温度测量误差，箱梁尺寸误差，大气温度设置误差等等。但总体来说，有限元拟合数据与试验数据在一天内的变化趋势一致，因此有限元方法可用于模拟日照环境下的箱梁温度场。

3 承重箱梁日照温度场有限元分析

3.1 有限元模型

由于国内目前还没有用于高速磁浮的大型箱梁，本文参考已有铁路工程实例及相关磁浮梁上梁式轨道梁专利，考虑人员逃生通道、设备检修通道以及车辆界限等因素，确定了箱梁截面尺寸，通过模态分析以及刚度分析，进一步优化了箱梁截面尺寸，优化后的箱梁截面如图7所示。

图7 箱梁截面(单位：mm)

本文假定箱梁的走向为南北走向，利用有限元软件ANSYS建立了有限元模型。有限元单元采用SOLID70单元，SOLID70单元在进行瞬态热分析以后能够通过单元转化命令成为SOLID185单元而进行结构分析，网格尺寸控制为0.1 m，模型材料采用C50混凝土。混凝土材料的热性能参数参考《高性能混凝土结构抗火设计原理》[14]：混凝土密度为2 400 kg/m3，导热系数与比热容分别为1.758 W/(m·℃)和916.7 J/(kg·℃)。

3.2 日气温变化

根据最近10年气温统计资料，上海市7月份平均最高气温为33.63 ℃，平均最低气温为26.88 ℃；青岛市8月份平均最高气温为29.14 ℃，平均最低气温为23.71 ℃。上海与青岛日气温变化曲线如图8所示。

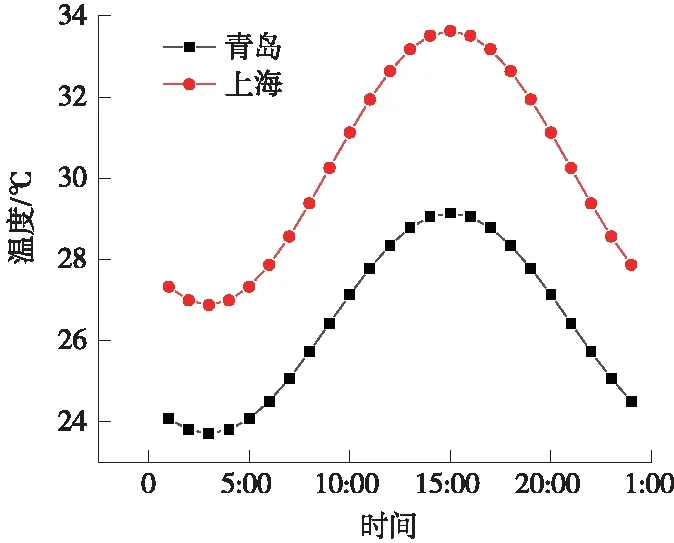
图8 上海与青岛日气温变化曲线

对于箱梁内部空气，其温度在一天内波动较小，可近似按式(2)计算[15]。

(2)

3.3 热交换系数

国内外许多学者[16-18]对对流换热系数进行了大量研究。对流换热系数hc主要与风速、表面粗糙度以及表面倾斜度等因素有关，其中风速起主要作用，对流换热系数可按照文献[19]计算。辐射换热是指物体与介质之间通过长波辐射的方式进行热交换，辐射换热系数hr可按文献[20]计算。上海与青岛的对流换热系数与长波辐射换热系数计算结果如表1所示。

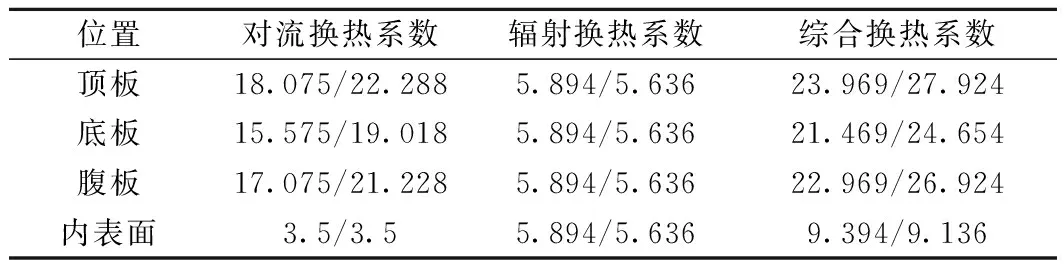
表1 换热系数 W/(m2·℃)

3.4 太阳辐射量的计算

对于处在大气环境下的箱梁，其受到的太阳辐射主要包括太阳直接辐射、天空散射以及地表反射。太阳辐射的计算可根据文献[21]的方法计算。太阳辐射量的计算结果如表2所示。

表2 太阳辐射计算结果 W/m2

4 ANSYS计算结果

4.1 箱梁温度云图

基于上述理论与计算结果，对箱梁进行24 h瞬态热分析。为了消除箱梁初始温度设置的影响，循环计算4个周期[5]。计算结果表明：第3个周期与第4个周期的结果基本一致，取第4个周期的计算结果，上海地区箱梁温度场云图如图9所示。

图9 箱梁截面温度场分布(上海)

由图9可以看出，随着太阳辐射入射角的变化，箱梁的温度也发生相应的变化。东腹板首先受到太阳辐射，因此东腹板的温度率先升高；随后，顶板开始受到太阳的辐射，此时顶板的温度逐渐升高。在下午时西腹板开始受到太阳辐射，此时西腹板的温度逐渐升高。由于受到太阳直接辐射的影响，箱梁的温度极值出现在顶板以及两侧腹板的外表面。对于箱梁底面以及内表面，由于受到的辐射较小甚至没有，因此其温度在一天内的变化不明显。

4.2 不同节点温度变化

国内外相关文献研究指出，箱梁沿轴向的温度变化基本保持不变[22]。因此，为探究竖向与横向节点的温度变化趋势，本节选取端部截面东腹板中线以及底板中线附近节点进行分析，节点位置如图10所示。

图11为箱梁竖向节点温度时程曲线。由图11可以看出，初始温度场的假设所引起的误差随着循环加载逐渐消除，第4个计算周期与第3个计算周期的结果基本一致，因此本文后面部分的分析均取第4个周期的计算结果。顶板受到太阳直接辐射，因此顶板节点N1在一天中的气温变化很大。相对于顶板，底板仅受到天空散射以及地表反射，其节点N5在一天内的温度变化较小。对于靠近腹板中部的节点，其在一天内的温度变化不明显且温度变化存在明显的滞后性，这是由于翼缘遮挡以及混凝土的热传导性能较差等多方面因素导致的。

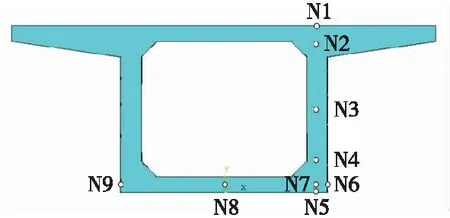
图10 箱梁端部节点选取示意

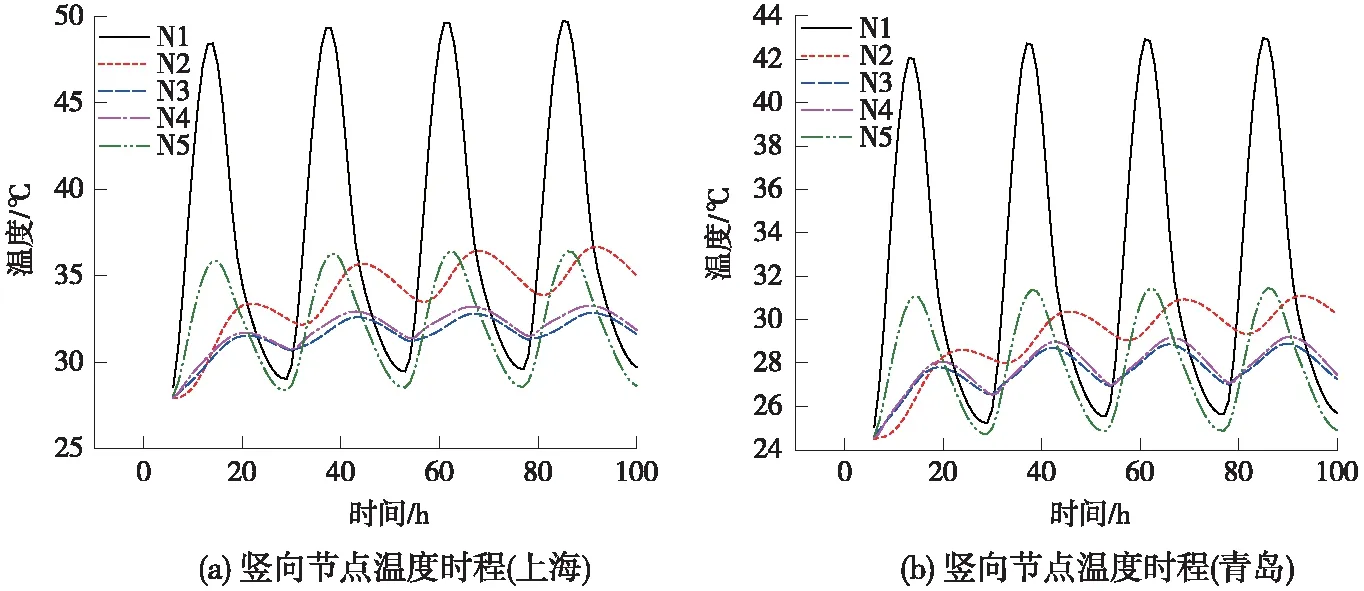
图11 竖向节点温度时程曲线

图12为横向节点温度时程曲线，由图12可以看出，东西两侧腹板的节点在一天内温度变化很大，中间位置节点在一天内的温度变化较小，这是由于东西侧腹板相比于底板在一天内受到的辐射总量更大。由于太阳直接辐射时间不同，东西侧节点温度时程曲线存在明显的相位差。东侧节点N6的温度在上午9点左右达到峰值，在此之前，东腹板底部受到太阳直接辐射，随着太阳辐射入射角的变化以及翼缘遮挡的影响，在此之后节点处于阴影状态，温度随之下降。西侧节点N9在一开始时温度变化较为平缓，在下午两点左右底部节点开始受到太阳直接辐射，此时节点的温度急剧升高，并在下午5点左右达到峰值。

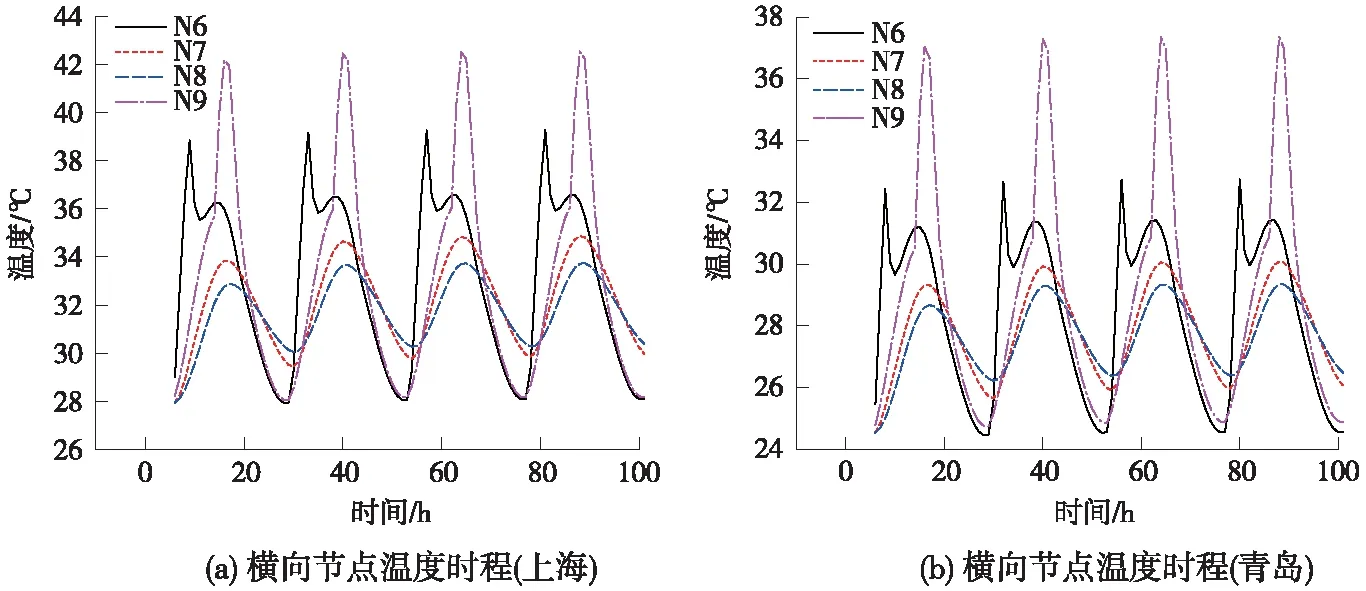
图12 横向节点温度时程曲线

由图11与图12可知，箱梁在两个地区的相同节点在同一时刻的温度不同。上海气温较高而风速较低，导致箱梁节点最大温度与最小温度均高于青岛，但箱梁节点温度随时间变化趋势一致。

4.3 最不利温差梯度拟合

4.3.1 最不利竖向温差拟合

由有限元分析结果可知，两地箱梁竖向最大温差均发生在下午2点左右。图13为箱梁最不利温差分布曲线，由图13可知，两地箱梁竖向温差分布趋势基本一致，靠近顶板0.6 m和底板0.2 m范围内的节点温差变化剧烈，中间部分温差变化较小，上海地区箱梁竖向最不利温差比青岛稍大。利用指数函数对上海地区箱梁最不利竖向温差进行拟合，顶板向下3.0 m范围内的拟合公式为T=17.54×e-6.04x，底板向上0.2 m范围内的拟合公式为T=4.36×e-6.80x。

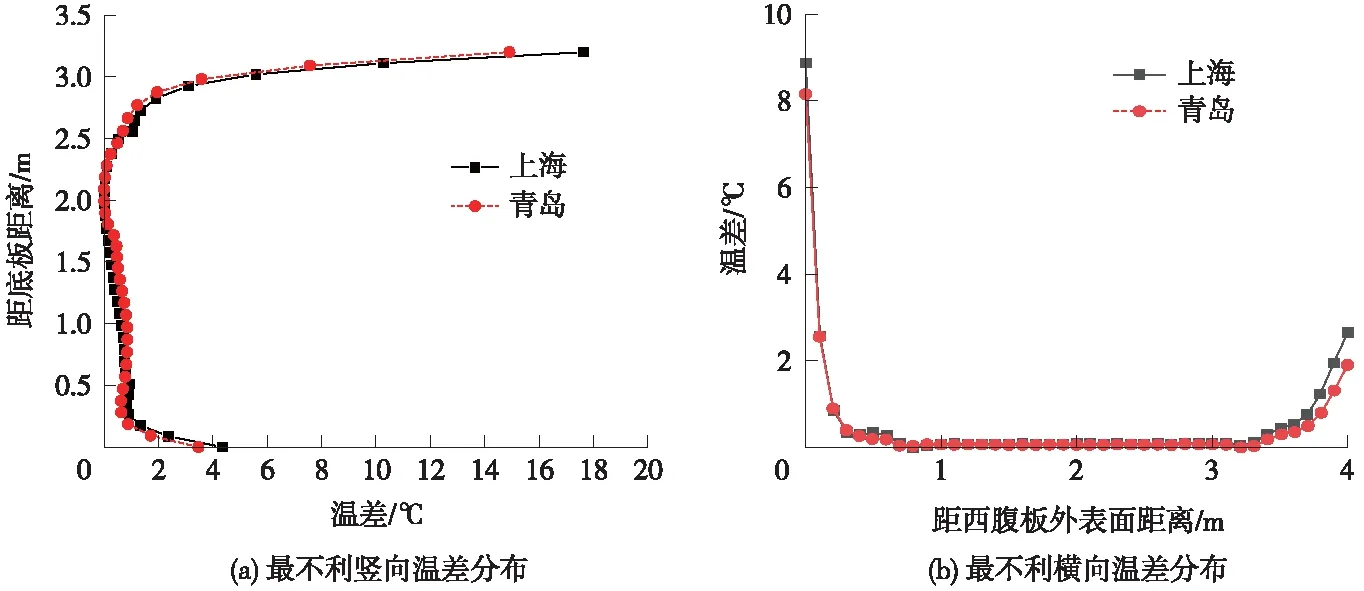
图13 最不利温差分布曲线

4.3.2 最不利横向温差拟合

两地箱梁横向最大温差发生在下午4点左右，由图13可知，东西腹板0.5 m范围内的节点温差变化剧烈，靠近中部节点温差基本为0 ℃，上海地区箱梁横向最不利温差较青岛大。利用指数函数对上海地区箱梁最不利横向温差进行拟合，西腹板向右3.5 m范围内的拟合公式为T=8.86×e-11.40x，东腹板向左0.5 m范围内的拟合公式为T=2.70×e-3.86x。

4.4 拟合公式与磁浮规范对比

我国《高速磁浮交通设计规范》[23]指出：磁浮轨道梁的温度梯度选取参照TB10092—2017《铁路桥涵混凝土结构设计规范》[24]的温度梯度模式，并结合当地试验梁温差实测数据取值。规范对于竖向温度梯度的规定是温差从顶面向下衰减，对于横向温度梯度的规定是沿梁宽方向衰减。由4.3小节可知，竖向温度梯度与横向温度梯度与规范存在较大的差异，主要表现为温度梯度不是沿单方向减小，在箱梁底部和另一侧腹板温差有明显的回弹。对于磁浮系统，轨道梁竖向温差变形控制要求十分严格，竖向变形过大会影响车桥耦合振动，因此有必要讨论规范对于温差的规定是否合理。

4.5 箱梁温度变形

现有文献对于箱梁温度变形的计算多是通过拟合温度梯度建立三维模型，将温度梯度作为荷载输入计算温度变形。本节分别计算了在规范公式、拟合公式以及三维温度场荷载作用下箱梁的温度变形并进行对比分析，其中利用三维温度场计算温度变形的方法此处称为直接法，温度变形云图如图14所示。

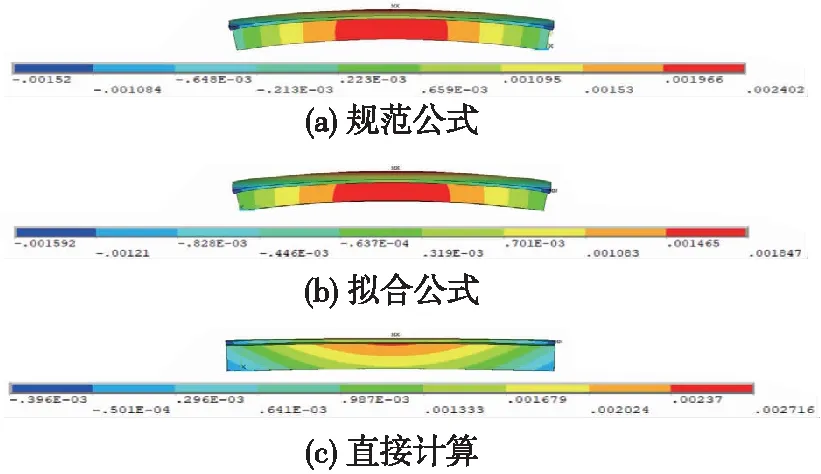
图14 箱梁温度变形云图

由图14可知，拟合公式计算的结果最小，规范公式计算的结果和直接法计算的结果相近，较为符合实际，规范公式相对于拟合公式更偏安全，实际工程中可采取规范公式进行计算，但仍需进行现场试验确保安全。直接法的箱梁变形云图相较于另外两种方法存在一定的差异，主要表现为温度变形不是沿中间向两侧减小，主要原因为箱梁温差不是与规范假设一致，对于处于同一个高度的节点来说，外表面节点和内表面节点温差不会为零，因此箱梁温差变形与规范计算结果有所差异。

4.6 风速对箱梁温差的影响

箱梁处于日大气环境时，风速相对其他因素来说难以控制。前面已经说到风速对于对流换热系数有较大的影响，风速越大，对流换热系数越大，箱梁与周围环境的热交换效率越高。实际环境中风向较难控制，本小节主要目的为探究风速对于箱梁温度梯度的影响，风向的影响可忽略不计。为了探究风速对箱梁截面竖向与横向温差梯度的影响，取风速分别为0，3.5，7 m/s和10.5 m/s，对上海地区箱梁进行有限元分析。

不同风速下箱梁的最不利温差如图15所示。由图15可以看出，风速不同时，箱梁的竖向与横向温差分布规律基本保持一致。当风速逐渐增大，箱梁与周围环境的热交换效应增强，箱梁的竖向与横向温差减小，箱梁的整体温度分布更加趋于均匀。我国幅员辽阔，不同地区风速以及风向相差较大，在对箱梁竖向与横向温度梯度进行规定时，应考虑当地气候条件。

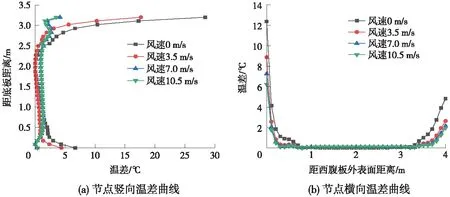
图15 不同风速下箱梁最不利温差曲线

5 结论

(1)在日大气环境下，上海与青岛两地由于大气温度、风速等因素不同，导致箱梁截面的最高与最低温度存在一定的差异，但箱梁整体的温度分布趋势相似，竖向与横向温度梯度分布相一致，实际工程中可采取同一种标准计算。

(2)箱梁竖向与横向温度梯度拟合结果表明，竖向与横向温度梯度与规范所规定的温度梯度存在较大的差异性，主要表现为温差不是沿单方向减小。

(3)箱梁温度变形结果表明，规范公式、拟合公式与直接法计算的结果相比，拟合公式计算出的竖向温度变形最小，因此不能忽略横向温差对于竖向温度变形的影响。规范公式更加贴合实际工程，相较于拟合公式偏于安全，实际工程项目可参考规范公式，但仍需进行现场试验。

(4)风速对于箱梁的温度梯度有较大的影响，随着风速的增大，箱梁温度梯度有减小的趋势。实际工程中，应考虑不同地区的气候条件，合理设置风速。