欧文·卡普兰斯基的数学人生

杨中明 王淑红

摘   要    欧文·卡普兰斯基是美国著名数学家、数学教育家、音乐家和科学组织者，他一生著书立说、领导机构，在数学的多个分支领域作出原创性成就，并为数学界培育了大批人才，为20世纪数学的发展作出了积极的推动作用。在研读和分析相关文献的基础上，主要对其生平、成就及影响作一简要介绍。

关键词    欧文·卡普兰斯基  代数学  美国数学会  美国国家数学科学研究所

中图分类号    N09： O1

文献标识码    A

2006年6月25日，美国国家科学院院士、美国艺术与科学院院士、美国数学会前主席、美国国家数学科学研究所所长、著名数学家欧文·卡普兰斯基（Irving Kaplansky，1917—2006，以下简称卡普兰斯基）在家中去世，终年89岁。他生前不但是一位杰出的数学家、数学教育家、音乐家，而且还是一位优秀的科学组织者，他为20世纪中后期数学和数学教育的发展作出了积极的推动作用。卡普兰斯基生前还与我国著名数学家陈省身（1911—2004）、华罗庚（1910—1985）、刘绍学（1929—）和周伯壎（1920—2009）等有密切的交往。

通过研读和分析与卡普兰斯基有关的文献资料，有一些问题很值得思考和借鉴。比如，卡普兰斯基在音乐上取得了不错的成绩，他为什么放弃音乐转而研究数学？在数学的众多分支领域中，他为什么对代数学情有独钟？他是怎样走上领导职位，为广大的数学工作者服务的？他又是如何与中国数学家密切交往的？通过探寻卡普兰斯基的人生轨迹，解析他在事业和生活上成功的密码，以期对他有更加深入的了解，并从中受到一些良好的教益。

一   一生求索，献身数学

卡普兰斯基于1917年出生在加拿大安大略省的省会多伦多市。在他出生前不久，为了躲避第一次世界大战的炮火，全家从波兰移民到加拿大。父亲萨缪尔·卡普兰斯基（Samuel Kaplansky）通晓《犹太法典》，求知欲强，是东欧犹太人所尊敬的学者，在波兰曾做过犹太拉比。但到加拿大后，他只能在多伦多做裁缝，收入极低，不足以维持整个家庭的生计。卡普兰斯基的母亲安娜具有事业心，为了补贴家用，她开了一家面包烘烤店。后来烘烤店发展成为连锁店，在多伦多颇具规模。卡普兰斯基自幼在面包店里帮忙，直到去读研究生离开家乡为止。

卡普兰斯基是一位著名的音樂家，他以高超的琴技著称。他四岁时，在只听了一遍的情况下，他就能准确地弹奏出《金雀》（The Golden Bride）这部喜剧中的热门歌曲。在坚持学了11年钢琴后，他认为即使继续学下去也没有太大意义，自己不会成为异于他人的钢琴家。他虽然没有选择音乐作为自己的职业，但音乐却伴随了他一生。在哈佛大学担任讲师期间，他加入了学校中的一个大型爵士乐队，很多学生因在音乐会看到他们的老师在弹奏钢琴而感到惊讶。在哈佛大学的广播电台，卡普兰斯基还有个固定的节目，被人们称为“K2”（Kaplansky Kapers）。后来，他用圆周率π的前14位数字谱写了一首歌曲“π之歌”。他的女儿露西·卡普兰斯基（Lucy Kaplansky）是一位音乐家，经常演唱这首歌曲。即使在年近九旬的时候，卡普兰斯基仍然经常上台弹奏钢琴[1]。

卡普兰斯基有杰出的数学天赋，他认识到“数学是他一生要追求的东西”[2]。在多伦多大学读大一时，他在参加了爱米·诺特（Emmy Noether，1882—1935）举办的一场学术报告会后，深受启发。后来谈到诺特对他的影响时，他将其奉为抽象代数之母。在此期间，他学习了大量经典数学的课程，为以后的数学研究奠定了良好基础，其中就包括理查德·布饶尔（Richard Brauer，1901—1977）的课程。用卡普兰斯基自己的话说：“我喜欢用代数的方式看待事物，这很大程度上要归功于布饶尔。”[2] 1938年，正在读大四的卡普兰斯基代表多伦多大学参加了由美国数学协会主办的第一届普特南数学竞赛（Putnam Mathematical Competition）并胜出，他获得了个人奖学金并进入哈佛大学深造。在哈佛，他师从著名数学家、美国数学会前主席桑德斯·麦克莱恩（Saunders Mac Lane，1909—2005），并于1941年获得博士学位，论文题目是“极大赋值域”（Maximal Fields with Valuations）。博士毕业后，卡普兰斯基留在哈佛大学担任本杰明·皮尔斯讲师（Benjamin Peirce Instructor），直到1944年。这一年，他跟随麦克莱恩加入了位于哥伦比亚大学的战时国防委员会下属的应用数学小组，主要从事火力控制设备与火箭投弹方面的数学研究。在这期间，卡普兰斯基把大部分时间都花在研究常微分方程上。正如他后来所言：“在这一年我体验到了现实生活的滋味，并发现数学实际上可以用来做一些事情。”[2]

1945年秋，卡普兰斯基受聘于芝加哥大学，直到1984年退休，他一直在大学任教。20世纪40年代的芝加哥大学数学系汇集了马歇尔·斯通（Marshall Stone，1903—1989）、陈省身、安东尼·齐格蒙德（Antoni Zygmund，1900—1992）、安德烈·韦依（André Weil，1906—1998）、麦克莱恩等世界级的数学大师，并且吸引了欧文·西格尔（Irving Segal， 1918—1998）、保罗·哈尔莫斯（Paul Halmos，1916—2006）、艾沙道尔·辛格（Isadore Manuel Singer，1924—）等一大批才华横溢的年轻数学家，他们对卡普兰斯基的数学研究产生了重要影响。卡普兰斯基回忆与他们的交往时，曾道：

我和韦依共事了近十年，如果没有他，我是不会做某些数学研究的。这并不是说他告诉我怎么做之类的，而是他随意的一句评论，就会让我开始做某件事……你可以选择一个他可能以前从未听说过的数学领域，冷不防地，他就会发表一些关于这方面的看法。同样，约翰·米尔诺（John Milnor，1931—）、迈克尔·阿蒂亚（Michael Atiyah，1929—2019）等能在合适的时间准确地说出正确的事，所以和他们交流是非常值得的。

我要向芝加哥大学的年轻同事西格尔、哈尔莫斯等人致敬，我和他们进行过一次次精彩而又激动的数学交流。比如西格尔，他曾致力于对C*-代数、局部紧群的表示论及相关主题的研究并积极地探讨它们与物理学之间的关系。我追随着他的足迹，最初我像个学生，过了一段时间我有种感觉，觉得自己可以和他平等地交流。[2]

卡普兰斯基的名字与一些伟大的数学定理紧紧联系在一起，如卡普兰斯基稠密性定理[3]、卡普兰斯基猜想、卡普兰斯基定理等。卡普兰斯基将自己的一生都奉献给了数学，即使在2006年临终前，他依然在研究丢番图方程。对于数学的发展，他曾评论说：“数学之所以发展到今天的高度，是因为我们站在了卡尔·高斯（Carl Gauss，1777—1855）等数学大师的肩膀上。”[2]孰不知他本人也是大师。

除了事业上的成功，卡普兰斯基还有一个美满幸福的家庭，他是一位忠诚的丈夫和优秀的父亲。1950年，他在一次聚会上认识了正在哈佛大学读研究生的妻子切雷·布伦纳（Chellie Brenner），次年结婚，后育有三个孩子（图1）。切雷风趣又富有幽默感，在她的影响下，卡普兰斯基的生活节奏缓慢而有序。卡普兰斯基的女儿露西是一位民俗音乐家，在她的回忆性文章“我的父亲”中，回顾了自己的成长经历。卡普兰斯基对子女的教育甚严，但又充满慈爱。在很早的时候他就教孩子们玩跳棋，培养他们分析问题、解决问题的能力。他教育子女做事要有条理、可靠、准时，给孩子们灌输一个贯穿一生的思想：赚钱并不重要，做自己热爱的工作就是一切。在孩子们的整个童年里，他们的父亲总是在书房思考数学问题。他们也曾问他们的父亲为什么如此喜爱数学，卡普兰斯基的回答是因为数学太美。

二   著书立说，培育人才

卡普兰斯基作为20世纪中后期有重要影响力的数学家，主要研究领域为代数学，在拓扑代数、环论、交换与同调代数、李理论和二次型等方面都取得了丰硕成果。为了表彰他对数学发展所作的推动作用，1989年美国数学会授予他斯蒂尔终身成就奖。卡普兰斯基生前曾毫不吝啬地表达自己对代数的钟爱，他言道：

我喜欢用代数的方法看待事物，而且当代数方法被应用到无限的对象时，我更加着迷。[4]

卡普兰斯基钟情代数学要追溯到1938年，还在读大学的他参加了芝加哥大学举办的暑期代数课程。在这期间，麦克莱恩作了一场有关赋值论的报告，内容清晰，给他留下了深刻的印象。从此，卡普兰斯基一直对赋值论着迷，并且赋值论成为他最初的研究领域，这也促成了他将代数学作为自己的主要研究方向。

卡普兰斯基一生笔耕不辍，著书立说。芝加哥大学时期是他研究成果发表的高产时期，特别是在1948—1952年的四年时间里，他发表了32篇论文。其中就包括他最具影响力的论文“满足多项式恒等式的环”（Rings with a Polynomial Identity）[5]，这篇论文开创了非交换代数的一个重要分支。他证明了一个基本结果：一个具有多项式恒等式的本原代数在其中心上是有限维的。根据谷歌学术的不完全统计，这篇论文的被引用次数已高达240余次。卡普兰斯基涉猎广泛，在概率论、组合数学等方面也有重要的研究成果，尤其是他晚年有更多的研究旨趣。阅读过卡普兰斯基著作的人都知道，他的著作以简短精炼而著称，文中没有啰嗦的证明或凌乱的公式，而是试图去构建一种框架，始终能给读者一种耳目一新的感觉。正如香港大学萧文强在评论卡普兰斯基的著作时说：

卡普兰斯基的著作有个共同的特征，其内容令人耳目一新，论述方式友善、不拘于形式（但数学上又是严谨的）而又清晰。作者快速、直接地给出主要观点，并选取优秀的实例加以说明。[4]

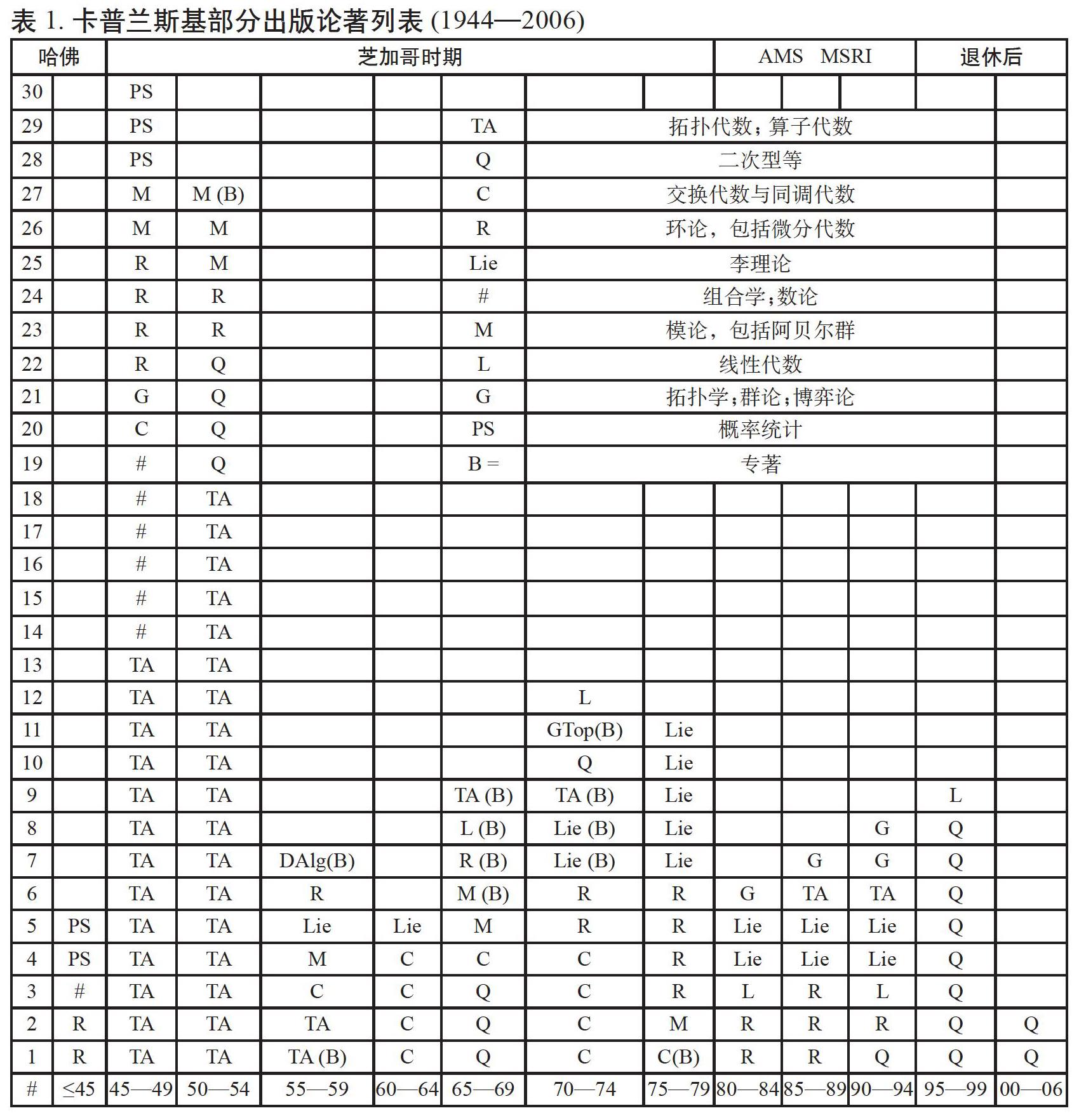
卡普兰斯基是一位多产的数学家，毕生发表了160余篇论文，出版《無限阿贝尔群》（Infinite Abelian Groups）、《微分代数导论》（An Introduction to Differential Algebra）等20余本著作，这些成果几乎都是关于代数学的。表1是根据目类的不同将卡普兰斯基的论文、著作进行了分类，他的部分著作早在20世纪七八十年代已经被引进到国内。

卡普兰斯基另一篇最引以为豪的论文是“任何正交补完备模格都是连续几何”（Any Orthocomplemented Complete Modular Lattice is a Continuous Geometry）。他的工作同冯·诺伊曼代数和连续几何一样，成为正交模格的重要理论来源。他在1955年发表这篇论文时，从事该领域研究的数学家还寥寥无几，有关著作和论文更是屈指可数，但目前这一领域已广泛被应用于其它学科。

卡普兰斯基最有影响力的专著是《无限阿贝尔群》，它将数学家的注意力从有限阿贝尔群转向无限阿贝尔群，也是第一部致力于系统地介绍这一领域的专著。对数学家的评判往往会通过对他研究贡献的深度和创造性来考虑。卡普兰斯基的专著，吸引了大批年轻学者进入这一领域。加州大学圣塔芭芭拉分校数学教授齐默尔曼（Huisgen-Zimmermann）曾回忆说：“卡普兰斯基是我的偶像之一。在学生时代，我发现了他那本关于无限阿贝尔群的书，并注意到代数也有很多故事要讲……”[4]

在1975年出版的专著《双代数》（Bialgebras）的附录部分，卡普兰斯基提出了有关Hopf代数的部分猜想，这就是著名的“卡普兰斯基十大猜想”。他本人并未对猜想做太多研究，但其他数学家对某些猜想的解决和物理学家林菲尔德（V. Drinfeld，1954—）所揭示的Hopf代数与量子力学Yang-Baxter方程之间的紧密关系，对Hopf代数的研究产生了巨大推动作用，并促成Hopf代数成为一个新的学科体系，如弱Hopf代数、Hopf群余代数等。东南大学王栓宏教授曾对这十大猜想的研究现状做过系统梳理[6]。

卡普兰斯基知识渊博，涉猎广泛，他属于有能力从事多项数学领域并从中获取灵感的数学家。早在1963年，我国的《数学文摘》杂志就系统介绍了卡普兰斯基在泛函分析领域的工作。他为泛函分析提供了一种公式化表示技巧，即“卡普兰斯基稠密性定理”。这个定理现已成为泛函分析研究的重要工具。理查德·卡迪森（Richard Kadison，1925—2018）将他誉为泛函分析领域早期最伟大的人物之一[7]。

卡普兰斯基是一位杰出的数学教育家。他教书育人，成就斐然。在芝加哥大学任教期间（1945—1984），他指导了55名博士生，这些博士生又培养了众多优秀弟子。根据数学谱系项目（Mathematics Genealogy Project）①的统计，卡普兰斯基至少有900多名再传数学弟子，而且随着时间的推移，这个数字仍在不断增加，这在1940年以后获得博士学位的美国数学家的弟子数量中排名高居第二。在教学生涯中，卡普兰斯基给学生们提出了很多有益的建议，这对我们的学习与科研有积极的启示。他最知名的建议是：“每天花些时间学习一些与你当前所处理的问题完全不相关的新东西（记住：这种不相关可能是暂时性的），并且要读大师的作品。”[4]经典著作经过了时间的检验，通过阅读既可以开拓眼界，提高知识储备，又获得优秀的思想和深刻的启示。向大师学习，才更有成为大师的可能。当一位伟大的数学家掌握了一门学科，读者通过阅读他的作品就能快速理解该学科的主要思想。卡普兰斯基对那些正犹豫是否要读数学系研究生的学子们说：“如果你还在纠结，那就算了吧。只有当你知道数学是你余生唯一想做的事情时才应该踏入这一领域，因为从事数学研究并不能得到很好的经济回报，而且会有很多挫折。”[2]

在卡普兰斯基的弟子中，不乏数学领域的佼佼者，他们现在很多人已经成为美国数学界的中坚力量。如：海曼·巴斯（Hyman Bass， 1932—），1959年他在卡普兰斯基的指导下获得芝加哥大学博士学位，主要研究领域是代数学。巴斯在1981年当选为美国艺术与科学院院士，1982年当选为美国国家科学院院士，2000—2006年担任国际数学教育委员会主席，2001—2002年担任美国数学会第56届主席。此外，他还是2006年美国最高国家科学技术奖获得者[8]。唐纳德·奥恩斯坦（Donald Ornstein，1934—）是卡普兰斯基的博士生，1957年毕业于芝加哥大学，研究领域也是代数学。在1970年，奥恩斯坦发表了论文“具有相同熵的伯努利移位是同构的”（Bernoulli Shifts with the Same Entropy are Homomorphic），在这篇论文中他提出了著名的奥恩斯坦同构定理（Ornstein Isomorphism Theorem），他也因此获得了1974年的博谢纪念奖（B?cher Memorial Prize）[9]。奥恩斯坦在1981年当选为美国国家科学院院士，1991年当选为美国艺术与科学院院士。卡普兰斯基指导的博士生还包括著名的数学家哈罗德·维多姆（Harold Widom， 1932—），他是波利亚奖获得者（2002）、维纳应用数学奖获得者（2006）。再传弟子则有著名华裔数学家林节玄（Tsit Yuen Lam， 1942—），他是巴斯的学生。林节玄1967年在哥伦比亚大学获得博士学位后进入加州大学伯克利分校担任教职。1982年美国数学会授予他斯蒂尔奖，以表彰他在教科书编著方面的贡献。1995—1997年期间他曾担任美国国家数学科学研究所副所长。卡普兰斯基的弟子们毕业后大部分进入高校，为数学界培养了大批人才，并且通过他们各自的研究工作，为数学的发展作出了各自的贡献。

卡普兰斯基尤其钟爱密歇根湖的海岸线，每天都坚持游泳，这在很大程度上锻炼了他的意志，强健了他的身体，使他在晚年仍有旺盛精力从事复杂的数学研究。在芝加哥大学的岁月里，他将课程尽量安排在早上，这样自己就能有更多时间与学生在一起。在课堂上与学生互动时，他鼓励学生提出质疑，支持学生用新的研究方法探討问题。斯蒂芬·尚努埃尔（Stephen Schanuel，1933—2017）关于投射分解的理论，就是由尚努埃尔在1958年秋天的芝加哥大学卡普兰斯基同调代数课程中所证明，这也是卡普兰斯基教学方法的最好验证，同时解释了为什么会有这么多的研究生选择他作为自己指导老师的原因。他经常为学生分享一些他还没有时间去检验但很有希望的新想法。正如巴斯所言：

恰当地说卡普的学生也是他全部作品中的重要组成部分。[4]

卡普兰斯基鼓励学生进行批判性思考，这对学生科研能力的培养是必不可少的。他充分尊重学生的独特性，在教学中帮助学生以自己特有的方式发展。当学生因为推测结果错误而产生负面情绪时，他鼓励大家应该树立正确的科研观，即在科学研究的过程中，探求真理所产生的消极结果和积极结果同样重要。例会是他与学生沟通的重要方式，每次例会开始时卡普兰斯基总会用“有什么新鲜事”作为开场白，随后便是一连串的问题：你能证明一个简单的例子吗？能否找出一个反例 [4]？卡普兰斯基激发了一代又一代研究人员来到芝加哥，向着数学的主题迈进。

卡普兰斯基生前与陈省身、华罗庚等多位中国数学家有密切的交往。他与陈省身在20世纪40年代的芝加哥大学便已相识（图2）。1946年1月，陈省身应阿德里安·阿尔伯特（Adrian Albert，1905—1972）的邀请，在芝加哥大学作了一场有关高斯-博内定理推广的报告，卡普兰斯基在这次报告会上结识了陈省身，虽然这次见面的时间非常短，但他对陈省身留下了深刻印象。1949年陈省身进入芝加哥大学任教，他们两人在芝大数学系共事了10年。1984年，他们的职业生涯在伯克利又交织在一起。卡普兰斯基曾回忆道：“虽然和陈省身的研究领域不同，但在与他的交往中通过相互渗透，自己也掌握了现代微分几何的部分精髓。”[10]20世纪80年代，华罗庚在美国访学期间，两人有一段交往的佳话。卡普兰斯基长期以来都不能解决无限维代数的半自构定理，虽然他得到了一个结果，但证明过程却极为繁琐，便请教华罗庚。没过多久华罗庚不但用另一种方法重新证明了这一定理，而且将证明过程简化到不足两页纸，完全解决了卡普兰斯基提出的难题，华罗庚使这个问题真正做到了“两点之间，直线最短”[11]。此外，我国著名数学家刘绍学、周伯壎等在芝加哥大学学习和访问时，与卡普兰斯基都有频繁的交往。

三   领导机构，誉满学界

卡普兰斯基生前不但是芝加哥大学数学系教授、美国国家科学院院士、美国艺术与科学院院士，而且还曾担任美国数学会主席、美国国家数学科学研究所所长，在1962—1967年期间还曾经担任芝加哥大学数学系主任。作为一名管理人员，他从未忘记导师麦克莱恩给他的建议：“随时都要表现得就像你必须在第二天向参议院调查委员会解释你的行为一样。”[2]

1984年秋，卡普兰斯基担任美国国家数学科学研究所第二任所长。他是最早提议创建高等数学研究机构的数学家，这是由于受普林斯顿高等研究院的启发。1946年，卡普兰斯基第一次去普林斯顿高等研究院访学，后来他将研究院描述为一个“那里人的数学热情几乎会自动流动、宁静的圣地……我为即将到来的关于非交换环、C*-代数、AW*-代数和其它一些东西的工作埋下了种子。换句话说，我得到了一个持续十年的数学推动力”[12]。卡普兰斯基倡议成立高等数学研究机构的想法最终在1982年得以实现，在美国国家科学基金会的支持下，在西海岸城市伯克利成立了美国国家数学科学研究所 [13]。卡普兰斯基正式接任所长后，他相继主持确立了不同年份的研究项目。研究所选择并确立项目主要坚持两条准则：⑴所涉及的主题应该是一个活跃的研究领域;⑵能将该领域的重要群体长期聚集在一起，且有助于丰富和提高该领域的活力。当被问及研究所是否已为数学的发展产生重要作用时，卡普兰斯基认为至少几十年的时间才能看到它带来的明显效果。以下为部分年度项目明细：

1984—1985：

低维拓扑（Low Dimensional Topology）、K-理论、指标理论和算子代数（K-theory，Index Theory and Operator Algebras）、微分几何（Differential Geometry）;

1985—1986：

计算复杂性（Computational Complexity）、数理经济学（Mathematical Economics）、几何函数论（Geometric Function Theory）;

1986—1987：

与代数几何有关的数论（Number Theory with Connection to Algebraic Geometry）、非线性扩散方程及其平衡态（Nonlinear Diffusion Equations and their Equilibrium States）、交换代数（Commutative Algebra）;

1987—1988：

經典分析（Classical Analysis）、巴拿赫空间的结构（Structures of Banach Spaces）。[14]

卡普兰斯基在担任所长的8年期间，为研究所的发展做了大量工作，其中一项成就是成立“美国国家数学科学研究所之友国际委员会”。这个委员会的主要职责是募捐，为研究所的发展获取源源不断的资金支持，这对机构的发展尤为重要。研究所除了将资金用于每年固定的重大项目开支外，剩余资金主要用于对年轻数学家的支持。研究所非常重视对刚毕业博士的培训和鼓励，预算中至少有60%的资金专门用于支持该类学者，如曼纽尔·巴尔加瓦（Manjul Bhargava，1974—，2014年菲尔兹奖获得者、2011年费马奖获得者、2005年拉马努金奖获得者以及1996年摩根奖获得者）就曾多次受卡普兰斯基的邀请访问数学研究所。

在担任研究所所长期间，卡普兰斯基除了安排年度计划，还注重于运作的每一个细节。当时每年访问研究所的人员大约有180人，有些人少则待两个月，多则待一年，与这些人员沟通是一项繁重的工作。他将这比喻成招募180名新教员，由于每个访问者的情况不同，需要处理大量的信件和电话。卡普兰斯基对研究所的热情是矢志不渝的，他曾经向继任所长大卫·艾森巴德（David Eisenbud，1947—）说，在担任所长的8年时间里，自己亲自阅读并签署了每一封研究所发出的邀请信[2]。

1985—1986年期间的卡普兰斯基须同时承担两项艰巨的任务：既要领导美国国家数学科学研究所，又要主持世界上最大的数学会——美国数学会。能同时担任这两大机构的领导人，这是对他数学成就的有力肯定。

在1985—1986年期间，卡普兰斯基接替朱莉娅·罗宾逊（Julia Bowman Robinson， 1919—1985）担任美国数学会第48届主席。他在担任主席的两年时间里，为学会带来很大变化。1986年，美国数学会负责在伯克利主办了第20届国际数学家大会，卡普兰斯基作为组委会成员为大会的顺利召开做了大量工作，要组织并负责近3500名参会者的会议是一项极为艰巨的任务。他使数学会焕然一新，其中就包括摆脱毁灭性的财务状况。但卡普兰斯基回忆起当选时的情景时，他却谦逊地说：

当被推荐为美国数学会主席时，我的第一想法是不配得到这个荣誉，毕竟，该职位的担任者在长达两年的时间内会被视为美国数学界名义上的领导人。[2]

他曾任多个杂志的编委，具体为《美国数学会通报》编辑委员会（1945—1947，1979—1985）、《美国数学会汇刊》编辑委员会（1947—1952）和《美国数学会会报》编辑委员会（1957—1959）等。卡普兰斯基代表美国数学会出席了1948年在安娜堡和1955年在斯坦福的会议并应邀发言。他在担任数学会主席期间，支持创办了重要的杂志《美国数学会志》（Journal of the American Mathematical Society）[15]，他通过精心挑选第一届编辑委员会来推动项目有序展开，最终在1988年顺利发行。此外，他还推动了美国数学会终身会员制的建立。约翰·厄文（John Ewing）对卡普兰斯基在美国数学会的工作做了形象描述：

四十多年来，卡普兰斯基一直活跃在美国数学会，在那段时间，他一直是一股推动力……卡普兰斯基为学会服务的最显著特点就是他的风格，他所从事的每项工作、他所做的每件事都是有力而优雅、雄辩而体贴、精力充沛而又彬彬有礼。[4]

四   小结

通过研究发现，卡普兰斯基不但是一位著名的数学家、数学教育家、科学组织者，而且还拥有美满幸福的家庭。他爱好广泛，精通音乐，乐于运动，又很长寿，其身上很多光辉的思想、语言和行为值得我们借鉴和反思。

从学术传承和数学创新方面来讲，卡普兰斯基的学生时代抽象代数学正蓬勃发展，诺特、麦克莱恩和布饶尔等数学家对他产生了重要影响。第二次世界大战的爆发致使大量数学家纷纷逃离欧洲，迁徙到科研环境更为优越的北美。此时美国已经取代德国和法国成为新的数学中心，而芝加哥大学又是美国数学的中心，这为卡普兰斯基科研能力的提升和学术思想的形成提供了丰厚沃土。通过阅读他的论著可知，他更倾向于为数学搭建一个框架，而非聚焦于某一特定数学问题。他始终主张数学家应该将注意力聚焦于领先性的数学问题，尝试一些其他人未来10年甚至20年都不可能研究的课题。他深受高斯的启发，强调论文重质而非量。他提出要在搞科研的同时学习一些与当前科研题目不相关的知识，这也是他能在诸多数学领域取得非凡成果的重要原因。

从培养学生，深耕数学教育方面来讲，卡普兰斯基极为重视数学人才的培养，他的很多弟子及再传弟子目前已成为美国数学界的中坚力量。在教学过程中，他鼓励学生大胆接受新事物，勇于探索新领域。他提出了正确的科研观，即在求索的过程中消极结果和积极结果同样重要。他采取讨论班的教学形式，根据学生的实际情况因材施教，注重培养学生的创新性思维。鼓励学生通过阅读经典论著以提高分析和鉴赏能力，达到开阔眼界、增长学识之目的。在长期教学过程中，卡普兰斯基形成了一套独特的教学范式。

从为数学共同体服务方面来讲，卡普兰斯基将科学组织视为推动数学发展的重要方式。他通过担任机构领导、杂志编委、数学会主席等，以不同角色服务于美国数学会40余年，促进了数学共同体间的交流和数学文化的传播。他是最早倡议建立美国国家数学科学研究所的数学家，他注重对青年学者的支持力度，推动了研究所建制的逐步完善。随着数学的发展越来越抽象，在数学界内部更难以进行无障碍交流的今天，数学组织的作用越来越明显，这充分表明卡普兰斯基提议新建高等数学研究机构的远见卓识。

最后，引用印度数学会对卡普兰斯基的评论来结束本文的内容：“卡普兰斯基教授是全世界数学家的灵感之源，人们将会永远怀念他的才智、魅力和人格。”[16]

参考文献

[1]蒋迅， 王淑红. 数学都知道1[M]. 北京：北京师范大学出版社， 2016. 92—93.

[2] Albers D. J.， Kaplanksy I.. Interview with Irving Kaplansky [J]. The College Mathematics Journal， 1991， 22（2）： 99—117.

[3]数学辞海编辑委员会. 数学辞海（第三卷）[M]. 北京： 中国科学技术出版社， 2002. 151.

[4] Bass H.， Lam T. Y.. Irving Kaplansky 1917—2006 [J]. Notices of the American Mathematical Society， 2007， 54（11）： 1477—1493.

[5] Kaplansky I.. Rings with a polynomial identity [J]. Bulletin of the American Mathematical Society， 1948， 54（6）： 575—580.

[6]王栓宏. Hopf代數的Kaplansky十大猜想的一些新进展 [J]. 数学进展， 2012， 41（3）： 257—265.

[7] Kadison. Irving Kaplanskys Role in Mid-twentieth Century Functional Analysis [J]. Notices of the American Mathematical Society， 2008， 55（2）： 216—225.

[8] Silicon. 2006年美国最高国家科学技术奖揭晓[J]. 激光与光电子学进展， 2007， 44（9）： 5.

[9] Ornstein D.. Bernoulli shifts with the same entropy are isomorphic [J]. Advances in Mathematics， 1970， 4（3）： 337—352.

[10]丘成桐，刘克峰，季理真主编. 纪念陈省身先生文集[M].杭州： 浙江大学出版社， 2005. 48—49.

[11]陆晓遐. 华罗庚[M].长春：时代文艺出版社， 2002. 81—83.

[12] Kaplansky I.. MSRI after three years [J]. The Mathematical Intelligencer， 1985， 7（4）： 48—55.

[13]张奠宙， 王善平. 陈省身传（修订版）[M]. 天津： 南开大学出版社， 2011. 156—160.

[14] Moore C.. Mathematical sciences research Institute Berkeley， California [J]. The Mathematical Intelligencer， 1984， 6（1）： 59—64.

[15] AMS.. 1989 Steele Prizes awarded at Summer Meeting in Boulder [J]. Notices of the American Mathematical Society， 1989， 36（7）：831—836.

[16] Yadav B. S.. Irving Kaplansky [J]. Ganita Bhāratī， 2006， 28（1—2）： 191.

Abstract： As a famous American mathematician， mathematical educator， musician and scientific organizer，Irving Kaplansky had lots of works and led organizations. He not only made original achievements in many branches of mathematics， but also cultivated a large number of talents for the field of mathematics and thus played a positive role in promoting the development of mathematics in the 20th century.Based on the study and analysis of the relevant literature， his life， achievements and influence were briefly introduced.

Keywords： Irving Kaplansky， algebra， American Mathematical Society， Mathematical Sciences Research Institute