16世纪英国学者约翰 · 迪伊的学术困境与科学探索

曹婧博

摘   要   约翰·迪伊作为英国都铎王朝时期的重要学者，积极推动并参与了欧几里得《原本》的英译工作，并为1570年比林斯利英译的《原本》作了一篇长达50页的《数学序言》。由于从事神秘学研究，迪伊的身份遭到了质疑，其学术贡献也常常为后世学者所忽视。通过解读《数学序言》的文本，可重新发现约翰·迪伊的学术思想及其对当时英国社会的积极影响，并从中窥见16世纪英国学者在科学方面的探索及英国科学发展的重要方向。

关键词    约翰 · 迪伊  数学序言  欧几里得原本  都铎时期的科学  神秘主义

中图分类号    N09： O1

文献标识码    A

一   绪论

1337—1453年期间，英国王室在百年战争中逐渐实现了转型（[1]，页342），同时摆脱罗马教廷和法兰克王国的干涉，使英格兰完成了向稳定统一的民族国家的转变，是英格兰王国民族化意识逐渐崛起的关键时期（[1]，頁413）。

16世纪末的英国处于都铎王朝统治时期，此时欧洲大陆的“文艺复兴”运动方兴未艾，英国的政治、社会与文化也处于重要的新旧交替阶段。都铎伦敦语作为一个重要的文化符号逐渐取代拉丁语和法语而成为官方语言[2]。一方面，以乔叟（Geoffrey Chaucer，1343—1400）、莎士比亚（William Shakespeare，1564—1616）的文学创作为代表的英国文化开始在文艺复兴运动中迎头赶上;另一方面，大量希腊语、拉丁语学术经典也开始被译为英语。1570年由亨利·比林斯利（Henry Billingsley，1532—1606）翻译的《欧几里得原本》（The Elements of Geometrie of the Most Auncient Philosopher Euclide of Megara，以下简称比氏《原本》）就是其中最重要的译著之一[3]。

在比氏《原本》的开篇，附有一篇长达50页的《数学序言》（The Mathematicall Praeface）。这篇《数学序言》的作者约翰·迪伊（John Dee，1527—1608）是一名活跃于当时的博学者，对数学、天文学、炼金术等学科均有涉猎，还曾担任伊丽莎白一世女王的御前占星师。他的私人图书馆①中藏有的丰富书籍和手稿[4]，是研究其学术特点的史料依据。《数学序言》是约翰·迪伊引以为傲的作品，狄博斯（Allen G. Debus，1926—2009）认为它是“纵观文艺复兴学术全貌的最佳文本”[5]，卡兹（Victor J. Katz，1942—）也高度评价了迪伊的《数学序言》，将其看作比氏《原本》中“最引人注目的部分”（[6]，页303）。

约翰·迪伊在《数学序言》中所构建的实用数学体系和他对实验科学与经验科学的思考给16世纪的英国数学发展提供了纲领。也是因为他的大力支持，比林斯利英译《原本》才得以顺利出版并广为流传，方便了很多数学爱好者进行阅读和研究，对于16世纪之后的学者产生深远影响。《数学序言》并非对前人的简单综述，迪伊吸收了弗朗西斯·培根、勒内·笛卡尔、帕拉塞尔苏斯（Paracelsus，1493—1541）等人在科学研究方面的思想，他尤其强调了各类实用数学及它们的技术上的实例和文艺复兴时期的神秘主义研究传统[5]。

但由于从事神秘学研究，迪伊曾遭受时人的反对和攻击，其学术贡献也常常为后世学者所忽视。他撰写《数学序言》的原因和其彰显的历史线索也几乎被埋于故纸。在这篇《数学序言》中，迪伊阐述了他对于数学学科实用价值的推崇，提出了他的数学谱系图，更义愤填膺地为自己所涉“黑魔法师”的污名辩白[7]。撰写该篇序言的历史原因及显露的历史语境给出了16世纪英国科学发展的清晰脉络。从这样一篇序言中，我们既可以了解约翰·迪伊对自然哲学的理解与思考，也可以考察都铎王朝时期神学、哲学、科学和神秘主义等思想领域间错综复杂的关系，以及它们对当时英国的政治与文化所产生的影响。

二   迪伊的学术困境：《数学序言》的历史语境

尽管在当时甚至更久远的古典西方文明之中，神秘主义与科学发展之间存在着相辅相成的关系——正如狄博斯所指出，强行区分文艺复兴时期著作中“神秘的”和“科学的”这两类知识，只会破坏那个时期的知识氛围（[8]，页16）。但即使在今天的学术史研究中，神秘主义及与其相关的史料仍处于被剥离状态。很多人物在学术史中扮演了重要的角色，后人却只能听到他们微弱的声音。其中就包括作为“科学革命中的重要形象”和“现代科学发展的主要贡献者”[9]的约翰·迪伊。

伊丽莎白一世（Elizabeth I，1533—1603）的时代是英国继承文艺复兴、发展本土文化的高峰时期。当时伦敦的思想活力为孕育英国的科学革命提供了土壤（[10]，页5），这一切与都铎时期列位国王对学术追求的热情是分不开的。伊丽莎白一世女王本人就撰写并翻译了多本学术著作，例如波爱休斯（Boethius，477—524）的《哲学的慰藉》（De Consolatione Philosophiae）[11]，也是迪伊在《数学序言》中和比林斯利在比氏《原本》中引用的重要文献之一。

而随着古希腊经典学术文献的翻译，有大批量的欧洲学者对古希腊哲学中的赫尔墨斯教派与新柏拉图主义的自然哲学产生兴趣，他们尝试融合古代“异教”知识与基督教思想，使神秘学在文艺复兴时期被一些基督教学者纳入罗马天主教的神秘哲学中 （[12]，页31）。

另一方面，伊丽莎白一世继承了父亲亨利八世（Henry VIII，1491—1547）的宗教政策，为摆脱罗马教廷对英国王室的控制而进行宗教改革，正式确立新教为国教。而新教中的强硬派对于教义则十分严格，他们指责占星学、魔法、卡巴拉思辨及与神秘学有关的柏拉图主义东方学都与福音毫无关系，并且认为受异教哲学影响而产生的基督教的希腊化是恶的真正起源（[12]，页69）。

迪伊在科学方面的才能无可置疑，但神秘学也一直是他非常热衷的领域。他为王室宫廷星占是出于研究星占学的需要，他为了寻觅炼金术中的哲人石而逐渐疏远了其他的工作。在迪伊晚年，他的所有精力几乎都被用于神秘主义和超自然研究 [13]。迪伊在神秘学研究上非常大胆。从1556年开始，迪伊出版了多本与占星、神秘学有关的书籍，并游说英国王室及贵族出资支持他的炼金活动，常把王公贵族的财富消耗一空[14]。他还研究灵媒和招魂，试图用天使来解释宗教、哲学和科学，他的“以诺克”（Enochian）语言也历来深为隐秘学家所关注（[12]，页36）。

迪伊的学术影响力吸引了新教徒抨击神秘学的火力，他的政敌和一些不明真相的民众也加入到抨击迪伊的行列中[15]。伊丽莎白一世给予了约翰·迪伊些许荣耀，但当他被指控为从事黑魔法研究并被污名化的时候，他所信赖的女王并没有站在他这一边（[10]，页159）。

在《数学序言》中迪伊加入了一段言辞激烈的自白书，他述说自己为了追求真理而经历的苦难，并对反对者的中伤予以反击：

“比疯人还要恐怖，是英帝國中危险的一员，不是基督徒”……你们这样称呼博学者吗？你们这样称呼哲学家和智慧的追求者吗？放弃天堂之路而在通向地狱的道路上挣扎？放弃天堂智慧之光而躲在黑暗之王的地牢里吗？放弃上帝的真理和他的造物吗？奉承欺骗、狡诈、顽固的说谎者难道不是给上帝的终极真理的力量丢脸吗？要放弃永恒的生命和福祉，追随永恒死神的创造者——那位贪婪偷窃人类灵魂的杀人暴君吗？[7]

反对者的“恶言恶语”和“友人的沉默”让迪伊十分受伤，他希望能够借助欧几里得的威名和《原本》“内在的声音”自证清白，在他的“哲学和数学的研究和实际操作中，从没有侵犯上帝或人类的法则”[7]。他希望反对者和冷漠的围观者都能理解他的研究工作，洗脱他“黑魔法师”的污名，从而与他一起在研究中寻找真理[7]。这才是迪伊最迫切需要面对和解决的问题，也是他最希望能借助序言而公布于众的自白。

面对反对者的污名化，迪伊坚持声称自己对宗教的信仰，他无时无刻不在强调自己是一名虔诚的基督徒，而绝非是令人望而生畏的“黑魔法师”。在《数学序言》自白部分的开篇，他一连用了四个反问来表达自己所学所做的一切都仅仅是为了寻求自然的真理，为了更接近全能的造物主的美德与智慧：

对于这些类似的奇观营造和自然的盛筵，数学和机械的设计，任何诚实的知情人士和谦逊的基督教哲学家应该被称为魔法师吗？

难道白痴的愚蠢、亵渎者的恶意胜得过不寻求世俗利益、只从上帝那里寻求天堂的智慧和纯粹真理的知识的人？

难道他若是寻求因永恒荣耀和全能的造物主而生的万物真谛和令人赞叹的美德，就会掠夺他令人尊敬的名和名望吗？

难道他就应该被暗地里诋毁为地狱恶犬的同伴，或者是邪恶该死的死灵法师吗？

有些人声称自己没有时间去学习这一切，但这确实是通向神圣智慧和真理的唯一途径。[7]

为了表现自己的虔诚，迪伊毫不吝惜笔墨。在《数学序言》论及星占学和静力学的部分以及文末，他都分别加上了祷告词：

诸天述说上帝的荣耀，穹苍传扬他手的作为，这日到那日发出言语，这夜到那夜传出知识。赞美上帝，赞美群星，赞美光。阿门。

神啊，谁人用公义建立了砝码与天平？谁人用数、重和量创造了万物？谁人将山川放置于天平之上？谁人在他们的手中量天测地？只有您，通晓万物。因此，神谕彰显了您的创造力，您在万物中显露了您的智慧，全能和无限的大善。而我们仅能瞥见事实的影子。我们应该意识到您在仁慈的大善中，用数、重和量这三种方法创造万物。数与量已经被人们（最有名，最古老，最重要的）知晓了，我们垦请您（通过您一贯的大善）让我们获得这第三把钥匙——重。您的仆人将用这第三把钥匙为您效力。为了荣耀您的名，我们将证明您的非凡的智慧的善。阿门。[7]

迪伊相信数学的感召力，认为在每一门数学技艺之中都存在无限的上帝和人类的创造力。但这恰恰是宗教保守派最不能容忍的一点——上帝之道是人不应窥视的大能，人必须因信称义，而不能擅自碰触自然的奥义。

在自然哲学研究的道路上，迪伊无疑是走得太远。他迫切想要了解自然的本质，不惜尝试各种方法，哪怕这些方法被普通人惧而远之。他兴致勃勃地在《数学序言》中谈论星占学和奇观营造学，并亲自设计并观察机械实验。他观察天体运行与尘世的关系，他认真钻研文献记载中的奇观营造，并借助卡西奥多罗斯①之口来赞美波爱休斯：

您的意愿是为了了解奇迹所彰显的深远奥义，在您的技艺中，您让金属燃烧出光芒，您让狄俄墨得斯从可以吹响的黄铜号角里走出来，您制作了一条可以嘶嘶作响的青铜蛇和可以甜美鸣唱的鸟儿。这仅仅是我们能记起的一小部分，您是能够复制天堂的人。[7]

迪伊也想成为波爱休斯那样的人，于是他设计了一鸣惊人、以假乱真的机械甲虫。当时人们无法理解这精巧装置的深意，来自新教的攻击者将迪伊的设计看作是奇技淫巧，迪伊也因此一生都未能摆脱“黑魔法师”的污名（[10]，页148）。迪伊希望通过知识的魅力来自证清白，并获得保守派的重新接纳。他曾在自白书中希冀着污名褪去的那一天，他甚至能像先贤一样获得后人的敬仰[7]。

在神秘学研究被正统学术拒之门外的时期里，迪伊的地位一度颇为尴尬。由于迪伊的神秘主义背景，在很长一段时期之内研究者们都对他的身份讳莫如深，而关于迪伊的文本解读更多见于非学院派的索引。暧昧的历史身份使得关于迪伊的秘闻野史十分丰富，数量大大超过正史中对迪伊事迹的记载和对其学术文献的研究。而随着研究视角的逐渐开放，尘封的历史文本被重新关注。虽然研究者们有时仍称其为“声名狼藉的魔法师”（the notorious magus）[16]，但他们已经开始重视并赞扬迪伊在科学史上的贡献。

三   《数学序言》与实用数学框架体系的建立

1.迪伊实用数学思想及其来源

1570年前后的英国社会，虽然在伊丽莎白一世女王的推动下涌动着文艺复兴的思潮，但人们对于數学这门学科的态度却是复杂的。很多人仍然将计数之学的神秘性等同于巫术或高高在上、只可远观的神谕（[10]，页144）。来自古希腊的欧几里得几何学知识，在大学的课堂上仅作为文学学士等学科的点缀。经院哲学在英国大学教育中占有主要地位，数学学习的主要作用仍是锦上添花（[6]，页248）。

约翰·迪伊对新教强硬派的态度不屑一顾，但他认识到现世的实用性对这些只想着“世俗的财产，世俗的尊严”的投机者们极具吸引力。所以在序言里，他反复强调数学这门学科及其18门衍生学科的实用价值。

实用数学的概念，是在14世纪伴随着意大利沿海地区商业活动的开展而逐渐兴起的（[6]，页271—272）。商业数学在私人教育机构开拓了市场，教师们在教材的封面上印刷引人入胜的标题来吸引学生[17]。雷科德（Robert Recorde，1510—1558）是第一个用英语撰写教材的英国数学家，为后世留下了多本重要的数学著作。雷科德在介绍几何学的时候，就将实用性作为学习数学最重要的目的之一。雷科德的《知识之途》（The Pathway to Knowledge，1551）①是第一部用英语出版的几何学书籍，其内容主要源自《原本》的前四卷[18]。在书中，雷科德用诗歌的体裁从各行各业的角度介绍了几何学的实用价值[19]。

约翰·迪伊很重视雷科德的工作，从其《数学序言》中援引的文献可知雷科德的《励智石》（The Whetstone of Witte，1557）是迪伊撰写《数学序言》的主要参考书目之一。雷科德在剑桥攻读博士学位时，约翰·迪伊也在剑桥读书。迪伊在私人图书馆中收藏了关于雷科德的书稿并做了详细的笔记[4]。雷科德离世之后，迪伊还曾重新编印过雷科德的著作《众艺之基》（The Ground of Artes，1543）[20]。结合迪伊《数学序言》的内容来看，他确实在很多方面受到雷科德的影响，比如《数学序言》中关于实用数学的论述和对于数学的许多阐释（如“金法”）。

在《数学序言》中，迪伊强调了天文学、测时学如何指导人们的日常事务[7]。针对商业活动，迪伊提到了比例混合法和试错法在商人分配资本、铸币及制药方面的用途，他认为这是代数学最具威力的部分，“应足够让任何理智的人都热爱、学习并操练这门算术科学并以此为荣”[7]。

关于建筑学，迪伊引述了维特鲁威（Vitruvius，公元前1世纪）和阿尔贝蒂（Alberto Alberti，1525—1598）来阐述其与数学之间相辅相成的关系[7]。建筑工程对于国家建设至关重要，它涵盖了房屋建造、军事防御和船只建造等三个实用领域。迪伊非常推崇建筑学，他为建筑学提出了一种专业复合型人才的概念，他认为一名建筑师的工作必须牢牢建立在几何、算术、光学、音学、天文、宇宙等所有出现在《数学序言》中的学科和其他自然技艺之上[7]。迪伊在《数学序言》中希望建立起如维特鲁威《建筑十书》（De Architectura）那样的“知识宝库”，将几何、算术、天文、音乐、人类学、文学和地球投影技术等技艺都融合在一起，给出指导读者的完美圭臬[7]。

迪伊还希望借助宗教的感召来鼓舞学生和读者，他认为仅仅学习七艺是远远不够的，应该将知识的范围扩大到更辽远的疆域：

我不怕那些只相信七艺之人的蔑视，甚至有些人可耻到否认七艺的存在。没有人能说清楚学科的数量。每一门艺术中都有无限的上帝、自然和人类的创造力。每一天都有新的艺术诞生。生有涯，知无涯。在这恩典的时刻，让我们拥抱上帝的恩赐与智慧之路，那些感恩的人们将得到无限的恩赐[7]。

迪伊相信数学研究中蕴含的巨大力量，他推崇知识的高贵，宣扬知识的实用性，更希望读者超越实用性去体会《原本》中的数学知识。他希望提升几何学研究在大学中的地位，也希望在大学之外有更多的人来研究《原本》。迪伊在《数学序言》中多次强调，任何人都需要多方面的知识，更不用说帝国所需要的专业人才。在迪伊看来，专业人才对各门实用数学技艺的掌握程度将深刻地影响国家的福祉。

2.迪伊所构建的数学框架体系

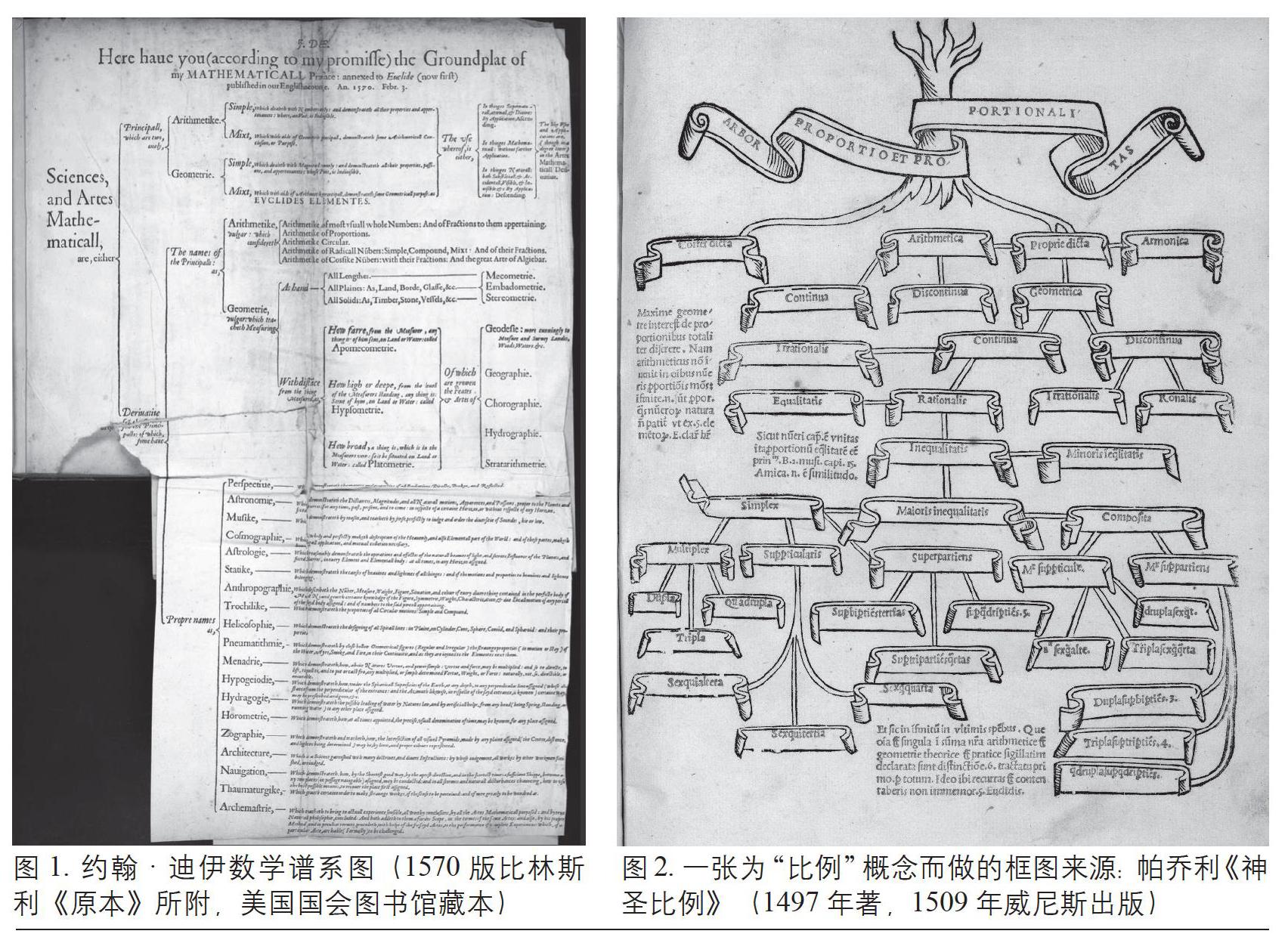
迪伊《数学序言》的附录中有一张数学谱系图（即被迪伊命名为“数学之树”的谱系图，以下简称为“谱系”，  图1）。根据迪伊在谱系前的记录可知其完成于《数学序言》之前[7]，是《数学序言》的提纲。迪伊在撰写《数学序言》之前，已经深刻思考了数学的学科结构。

西方数学学科的分类，最早或可追溯到公元前4世纪柏拉图的《理想国》，其中将青年所需学习的四门数学课程分为算术、几何、天文学和声学。公元5世纪，波埃修斯《算术原理》中首次提出四艺（quadruvium）一词 ，以此来称呼柏拉图所言的四门学科[21]。

树状谱系图在帕乔利（Luca Pacioli，1447—1517）的《神圣比例》（De Divina Proportione，1497，图2）和逻辑学家彼得·雷默斯（Peter Ramus，1515—1572）的教育学图标中已有先例（[10]，页159），但迪伊首次以谱系的形式来定义一门学科的体系结构。“谱系”清楚地反映出迪伊对数学学科的布局思想。首先是两大分类：一是数学的基础，二是由数学衍生而来的各类学科。数学分类的基石为算术与几何，二者都是由一个微小得不可分割的单位为起点，生成一门繁复的学科。同时算术与几何互相呼应，可以在另一方出现不能解决的难题的时候提供帮助[7]。

迪伊在《数学序言》中解释了数学之树的根基——“数”与“量”的基本定义。首先，定义“量”的最小单位为“元”（unit），数的最小单位为“一”（one），它们都是不可分割的最小单位：

我们将“数”定义为某种“单位”的总和。“元”是不可分割的数学之物。因为“单位”与或可称之为“一”或表现为“一”的事物在特性上相像，所以可顺理成章的将“元”称为“一”。我们将“元”视作数学之物，虽然它不是数，不可分。实际上，“数”是最终的数学之物，因为它由数组成。“量”也是数学之物，任何天然与长宽高有关的事物都是“量”……首先，我们把“数”及与之相关的数学科学称之为算术。其次，我们把“度”及与之相关的数学科学称之为几何。[7]

可以说，约翰·迪伊是首位将数学素养与英格兰的福祉联系起来的数学作家（[10]，页161）。后来也正如迪伊所预料的那样，他所构建的实用数学的理念和体系影响了几代学者的研究方向。虽然他们几乎闭口不提他的名字，却将他学说中最重要的内容默默地继承了下来。“黑魔法师”迪伊的学术主张为英伦小岛成长为大英帝国做出了突出的贡献，但他的名字却成为了女王甚至学者们心知肚明但有意隐去的一段秘事。他们拒绝承认神秘学研究属于自然哲学研究的一部分，并拒绝承认与神秘学相关的学者的合法地位。无论是出于宗教保守派的信条还是对未知的恐惧，他们烧毁了迪伊的图书馆（[8]，页19），并将一位研究者置于孤立无援、四面楚歌的境地。

2.几何学与机械天平实验

机械设计是迪伊擅长的领域，在《数学序言》中，迪伊讲述了自己如何在机械制造和设计砝码实验的时候应用《欧几里得原本》中的命题，这是迪伊机械设计中比较简单的一个实验。他用了大段的笔墨详细描述了用天平标尺测重和制作等比例砝码的场景：

为了完成静力学这一节，我将提供给您两三种实践应用。首先我们要用机械装置来研究砝码的数学。在同样的范围下放入立方和球体，让立方体的边与球体的直径相等。你可以用木头，铜，锡，铅或者银这些一直很重的东西来制作（立方体或球体）。因为天平标尺准备了很多小的砝码，所以你可以精确的测量六，八或者十二英镑的物体。要知道在天平标尺上有多少最小砝码可以用来配衡。[7]

迪伊根据比例论和立体几何知识设计了一个天平测量试验，天平砝码的重量需要根据比例来设计。实际上，早在柏拉图时代，古希腊人就开始研究立方体之间的比例问题①。在机械设计师的工作中，他们可以不根据几何学知识就设计出符合比例学的砝码。

欧几里得《原本》第十二卷包括18个命题，涉及运用欧多克斯穷竭法来解决立体图形中面积与体积的比例关系和计算问题。迪伊十分重视这一章的内容，在《数学序言》中，他认为立方体与圆柱体都与球体有特殊的比例关系，这一点可以结合阿基米德立体图形学说中的内容，来设计不同型号的砝码[7]。

迪伊提到了自己在比氏《原本》第十二卷末尾的证明，那是一篇关于球体、锥体、圆柱体和其他固体中的几何学定理和问题的论文，是比氏《原本》中最精彩的一篇注释。迪伊在其中增補了20道命题（8条定理和12道题）及若干推论，利用比例论来计算立体图形的体积问题。以其中最简单的引理为例，如果A：C等于6：1，B：C等于4：1，则A：B等于6：4。这是迪伊根据圆柱体中的圆锥计算得出的引理。

迪伊给出了三个常率——立方体与内接球，圆柱体与内接球及正方形与内接圆的比率，并提到了自己在欧几里得《原本》第十卷命题2①之后所附的一篇包含9道题和6个推论的小论文。迪伊认为在这个问题中蕴涵着数学王国宝藏的钥匙[7]。

迪伊用欧几里得《原本》第六卷命题12②来解释倒置三角锥体水位位置确定的标准。之后，迪伊在设计中运用了经典倍立方问题的计算，并提到了对欧几里得《原本》中第六卷命题10和第十一卷命题33的引用。第六卷命题10的内容是“当多个几何量与同一几何量相比较时，比值较大的一边的量大于比值较小的量”。所以当往倒置三角锥体中倒水的时候，可以根据这条命题来判断水的体积。而第十一卷命题33的内容为“相似平行六面体的比值等于对应边的立方比”。所以在制作椎体的时候，可以根据这条命题来设定椎体的大小：选取两条比例线段，分别以它们为高来制作锥体。而根据命题11—33，一个锥体的体积是三倍的底面积乘以高，这两个锥体的体积和他们的边比例相等。所以可以得到两个锥体之间的体积比。

迪伊根据自己的机械设计（图3）经验给出了最关键的结论：

任何球体，混合体或任何不规则体都可以由第一个已知比例的已知立体形构成。[7]

他提到了欧几里得《原本》第十一卷中的命题34与36。命题34讨论的是相等的平行六面体的底和高之间一定是反比例关系，而反之亦然，即两个平行六面体之间的高与底呈反比例关系的时候，这两个平行六面体是相等的。而命题36的内容是“如果有三条线段成比例，那么，以这三条线段作成的平行六面体等于中项上所作的等边且与前面作成的立体等角的平行六面体”讲述的是如何借助成比例线段来构建平行六面体。

迪伊特别重视欧几里得《原本》的立体几何部分，因为这一部分中给出的命题都可以在机械实验的设计中直接应用。也许因为如此，迪伊对第十卷到十三卷的内容作了十分详细的研读，并给出了大量的注释。他重视比例计算，认为机械师可以根据比例来制造任意大小的装置：

因此，根据人体模型（如荷兰画家所称），一个巨人可以获得同样的对称性。人体模型可以做到的姿势，巨人也可以做到（反之亦然）。那么，根据任何模型或船模，你可以造出任何比例大小的相似模型。那么，根据任何火炮或小原型你都可以造出你想要的大小（所有点都符合相同的体系）。[7]

迪伊希望通过自己的设计展现数学的魅力，他说：

数学思想可以（通过良好的方式）凌驾于星辰云朵之上，也可以屈尊迂贵行走于凡间。只要它愿意，人类可以回到自己的中心，在那里铺就上升或者下降之路（皆为了神的荣耀和人类诚实的欢愉）。[7]

研究者可以通过数学来设计和制造一切有用之物。

3.航海帝国的神秘顾问与复合型专业人才的培养理念

迪伊曾长期担任英国航海探险活动的顾问，然而他关于航海和航海仪器的论文手稿大多失传，只在他后来的自传中留下了只言片语[13]。在迪伊担任航海顾问的日子里，他亲自培养了很多航海人才，为航海事业的发展提供技术支持，参与航海仪器的设计实验。

迪伊在《数学序言》的航海部分中给出了他于1559年撰写的航海必备仪器的种类，并对航海家基本素养做出了规范[7]。他认为航海家及参与者应该具备基本的数学知识，其中包括罗盘的使用、天文的知识和航道的计算及重要的航海商业和探险所获财产的分配问题[7]。

对于英国航海事业的发展，迪伊的视角是专业且严格的。迪伊对于航海的理解并不局限于航海本身，他将天文、数学与机械技术与航海相结合，总结出了作为英国航海家所需要的基本素养。他认为航海家们需牢记柏拉图的指示“在战争中及时改变路线的重要性绝不亚于在农牧业和航海中” [7]。迪伊认为一名合格的领航员与建筑师一样，应该是一个专业的复合型人才——就像他在《数学序言》中多次强调的那样——需要掌握海洋地理学、天文、占星术、测时学的知识以及所有技艺的共同基础——算术和几何[7]。因此领航员必须能理解所需的各种工具，如象限仪、天文环（the astronomers ring）、天文杖（the astronomers staff）、通用星盘、水文地球仪、水文图、通用海洋指南针、特异的指南针等等，他应该学习在地球或平面地图上使用复合指南针的不同的方法，并且能够在任何给定的时间内计算行星的位置;另外，他需要知道出发港的确切经纬度，以便于在他能在准确定位的时候保持精确的航海日志;需要能够观察某些固定的恒星以及它们的起落;需要预测暴风雨、大风暴、海上龙卷风和其他在海上会引起危险的气象现象[7]。而欧几里得《原本》无疑是最合适的研究教材，通过研读几何学，人类可以深刻理解数学知识在这项伟大事业中的真正用途。

迪伊写道，“上帝赋予我们这座岛屿，就是将我们安放在一个可以驶向任何富足之地的地方”[7]。英国航海事业的发展正如迪伊所希望的那样，成为英国走上历史舞台成为世界强国的重要契机。这项对于英国人而言的伟大事业，不仅仅促进了英国渔业的发展，更增强了英国的经济实力，也为后来英国的扩张殖民提供了经济基础和技术条件。作为英国航海事业的主要推动者，迪伊的贡献既体现在了《数学序言》的文本中，又落实到了文本之外的现实世界。

参考文献

[1]戴维斯. 欧洲史·上卷[M]. 郭方， 刘北成等译. 北京： 世界知识出版社， 2007. 342.

[2] Mugglestone， Lynda. The Oxford history of English[M]. Beijing： Foreign Language Teaching and Research Press， 2011. 87.

[3] Archibald， R.C. The First Translation of Euclid's Elements into English and its Source[J]. The American Mathematical Monthly， 1950， 57（7）： 443—452.

[4] Roberts， Julian & Watson， Andrew G.. John Dee's Library Catalogue[M]. Oxford： Oxford University Press， 1990.

[5] Dee， John. The Mathematicall Praeface to the Elements of Geometrie of Euclid of Megara （1570） [M]. New York： Science History Publications， 1975.

[6]卡茲. 数学史通论（第2版）[M]. 李文林等译. 北京： 高等教育出版社， 2004.

[7] Dee， John. The Mathematicall Praeface[A]. Billingsley， Henry. The Elements of Geometrie of the Most Auncient Philosopher Euclide of Megara[C]. London， 1570.

[8]狄博斯. 文艺复兴时期的人与自然[M]. 周雁翎译. 上海： 复旦大学出版社， 2000.

[9] Clulee， Nicholas H.. Review： The Mathematical Praeface to the Elements of Geometrie of     Euclid of Megara（1570）[J]. Historia Mathematica， 1976， 3（3）： 355—357.

[10]哈克尼斯. 珍宝宫——伊丽莎白时代的伦敦与科学革命[M]. 张志敏， 姚利芬译. 上海： 上海交通大学出版社， 2017.

[11] Hume， David. The History of England from the Invasion of Julius Caesar to the Revolution in 1688[M]， Indianapolis： Liberty Fund， 1983.

[12]哈内赫拉夫. 西方神秘学指津[M]. 张卜天译. 北京： 商务印书馆， 2018.

[13] Easton， J. B.. DEE， JOHN[A]. Gillispie， C. C. （ed.）. Dictionary of Scientific Biography（vol. 4） [C]. New York： American Council of Learned Societies， 1970. 5—6.

[14] Farrington， Benjamin. The Philosophy of Francis Bacon[M]. Chicago： University of Chicago Press， 1966. 14.

[15] Clucas， Stephen. John Dee： Interdisciplinary Studies in English Renaissance Thought[M]. Dordrecht： Springer， 2006. 2.

[16] Malet， Antoni. Renaissance Notions of Number and Magnitude[J]. Historia Mathematica， 2006， 33 （1）： 63—81.

[17]马忠林. 数学教育史[M]. 南宁： 广西教育出版社， 2001. 300.

[18] Howson， Geoffrey. A History of Mathematics Education in England[M]. Cambridge： Cambridge University Press， 1982. 15.

[19]汪晓勤. 数学与诗歌：历史寻踪[J]. 自然辩证法通讯， 2006， 28（3）： 16—21.

[20] Cajori， Florian. Robert Recorde[J]. The Mathematics Teacher， 1922， 15（5）： 294—302.

[21] Schrader， Dorothy V. DE ARITHMETICA， Book I， of Boethius[J]. The Mathematics Teacher， 1968， 61 （6）： 615.

[22] J. 克萊因. 雅各布·克莱因思想史文集[M]. 张卜天译. 长沙： 湖南科学技术出版社， 2015. 44.

[23] Dee， John. The Works of John Dee： Modernizations of His Main Mathematical Masterpieces[M]. Egan， James A. （trans.）. Newport： Cosmopolite Press， 2010.

Abstract： As an essential scholar of the British Tudor period， John Dee actively promoted and participated in the translation of Euclids Elements， and wrote a 50-page Mathematical Preface for Billingsleys translation of the Euclids Elements in 1570. For devoted himself to the mysticism research， Dee had suffered from the opposition and attack， his academic contributions are often ignored by other scholars. The textual interpretation of the Mathematical Preface re-discovered John Dee's academic thought and its positive influence on British society during Tudor， and also described the struggling that Dee experienced，analyzed English scholars scientific exploration and the important directions of British science in the 16th century.

Keywords： John Dee， The Mathematical Preface， Euclids Elements， Renaissance during Tudor， mysticism