音乐中的数学

冯尤嘉

肉眼可见的数字和音乐

音符与数字

在简谱中，我们最为熟悉的音符do至si被表示为数字1～7。在数学中，数字0～9组成了千奇百怪的算式，因此，音乐中的1～7也能构成千变万化的乐章。

值得一提的是，钢琴键在一个八度中共13个键，由8个白键与5个黑键组成。其中5个黑键又分成2个一组和3个一组，正好和斐波那契数列（黄金分割数列）中连续的5个数字——2、3、5、8、13重合，不得不说是一个美妙的巧合。

节拍与分数

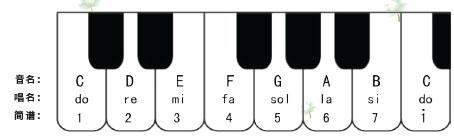
钢琴黑白键上的音名、唱名、简谱

在一首音乐中，我们时常会听到几个乐章，乐章中又分成小节，小节又能细分成不同的音符。每个音符所对应的节奏都能够用分数来表示，例如八分音符代表着1/8，即8个八分音符能够组成一拍。利用不同长度的音符，自然就能组成各式各样的节拍，而这些都能够用分数来表示。以民族乐曲《茉莉花》举例，第一个小节分别由1个四分音符和6个八分音符组成，写作算式就是：1/4 + 1/8 + 1/8 + 1/8 + 1/8 + 1/8 + 1/8 = 4/4，正好是一个小节。在更复杂的编曲中，要用到各种长短不一的音乐符号，涉及各种附点音符和休止符，可以说要想编出精妙而严谨的曲子，还需要掌握数学知识才行。

旋律与几何

在编曲中，比较常用的一种手法是将一段旋律以相同的节奏，但整体向上或向下挪动几个音符。用数学几何来解释的话就是“平移”。例如贝多芬著名的《命运交响曲》（又名《c小调第五交响曲》），乐曲开头充满了震慑力，再细看乐谱，我们能够清晰地看出，后两个小节是将前两个小节的音符进行了垂直平移，使得后两个小节的音调整体变得更为深沉和强烈。

《命运交响曲》乐谱进行的几何平移

还有一种编曲手法被称为“逆行”，即将一段旋律从后向前重复一遍，使旋律形成左右对称的“镜像”。这一手法在谱面上的表现，不正像在平面直角坐标系上的水平翻转吗？

在编曲中用到的“逆行”手法，使旋律形成左右对称的“镜像”

编曲美学与黄金分割

黄金分割可以说是数学在艺术领域上的一个突出体现。在一个线段AB中，取一点C，使得AC∶BC = BC∶AB，而这个比值就是0.618。

黄金分割线

有趣的是，在许多著名的音乐作品里，高潮往往安排出现在一首曲子中心点偏后的位置，从而在乐曲中形成了“黄金分割”比例。例如肖邦的《降D大调夜曲》，不计算前奏的话共有76小节。76x0.618=46.97，按照黄金分割的理论，高潮部分应该出现在46小节。而《降D大调夜曲》力度最强的高潮正是出现在46小节，可谓是对黄金分割的绝佳诠释。另据美国数学家乔巴兹统计，莫扎特的所有钢琴奏鸣曲中有94%符合黄金分割比例，不禁令人感叹这是多么奇妙的巧合。

艺术之美都是贯通的，无论是我们熟知的绘画、雕塑作品，还是音乐作品，只要其中运用了黄金分割，

弦振动频率示意图

那这样的作品往往更受人青睐，这无疑是数学在音乐乃至艺术中的体现。

优美的弦振动公式

提到音乐，就不得不提乐器。在乐器中，具有一定的规格是十分重要的。乐器的每根弦、每个气孔、琴码或踏板的位置都要根据标準精心调试，达到分毫不差。否则，一件乐器在不同的师傅手中，就会出现不同的调式。如乐团中常见的乐器长笛，通过向管内吹气，气流在管中碰撞，并通过共鸣管产生共鸣，按下按键则能够改变笛声的音色音调。这样精妙的设计，自然需要统一的制作，因此我们看到在市面出售的长笛也会标明笛子的规格。

制作乐器利用的就是声音的振动原理。18世纪，英国数学家泰勒发现了弦振动频率的公式：                   其中f表示频率;l表示弦的长度;T表示弦的张力;ρ表示弦的密度。

这表明对于材质与粗细均相同的一根弦，频率与长度成反比;相差一个八度的两个音振动频率之比为2∶1。按照这个标准，我们就能够准确地测量乐器的音高了。假定一根空弦发出的声音是do，则1/2长度的弦发出的是高八度的do;以此类推，8/9长度的弦发出re的音，64/81长度的弦发出mi的音，3/4长度的弦发出fa的音，2/3长度的弦发出so的音，16/27长度的弦发出la的音，128/243长度的弦发出si的音。若要发出高八度或低八度的音，也可以通过此公式来推理得出。

乐器是按照一定的规格制定的，而规格的统一就是标准化，标准化其实就是数学化。这样统一化的生产过程，就是数学参与在音乐中的最好证据之一。

热爱音乐的数学家

数学家与音乐的关系可以追溯到古希腊毕达哥拉斯学派，该学派信奉“万物皆数”，认为世界是严整的宇宙，整个天体体现着数的和谐，这种和谐使浩瀚无垠的宇宙处于一种纷繁有序的永恒运动之中。毕达哥拉斯学派强调宇宙天体、音乐、数字、神和人的心灵之间的和谐关系，提出了“美是和谐”的概念。一次，毕达哥拉斯路过一个铁匠铺，悦耳的打铁声引起了他的注意。于是他走入店中仔细观察，发现有4个铁锤的重量比恰为12∶9∶8∶6，将它们分成两两一组来敲打，都能发出和谐的声音。他们的组合包括12∶6=2∶1的组合，12∶8=9∶6=3∶2的组合，12∶9=8∶6=4∶3的组合。毕达哥拉斯进一步用单弦琴加以验证，最终经过反复实验，他将这几种美妙的音调归结为：八度音、五度音和四度音，对应2∶1、3∶2和4∶3。这可以说是最早用数学方法研究和谐美的实例了。

毕达哥拉斯用单弦琴反复实验创造出八度音、五度音和四度音

毕达哥拉斯还曾提出十二等程律（又称十二平均律）的概念。在之前我们已经了解到音是由振动产生的，十二等程律指的就是将一个八度的频率平均分成十二等分，每分相差一个半音，也就是100音分，是最主要的调音法。用数学的方法表示，就相当于一个有12项的等比数列。每个音的频率都为前一个音的2的12次方根。而明朝数学家朱载堉则在1584年将其理论化，他是世界上首位推算并制造出十二音律乐器的人。在当时常用五声音阶“宫、商、角、徴、羽”的中国，是他力排众议，创造了十二音律，也就是我们现在常用的七声音阶。他用竹子制造而成的36根律管，分别为倍率管12根，正律管12根与半律管12根;其口径、长度都经由严密的测算得出，是世界上最早的十二音律乐器。

朱载堉设计制造的律管分别为倍、正、半三种规格

无独有偶，德国著名作曲家巴赫所著的《平均律键盘曲集》，根据名称来看，可能就是为了十二音律乐器所设计。东西方的数学家们刻苦钻研十二音律，努力算出更精確的比率来使乐器的音调达到完美。最精确的比率换算成小数大约为1.059464094，即100音分。

古往今来，数学界的许多伟人也被音乐的魅力深深打动。英国数学家西尔维斯特曾说：“难道不可以把音乐描述为感觉的数学，把数学描述为理智的音乐吗？”，来自法国的傅立叶则认为，所有的乐声都能够由数学表达式来描述。

创立了笛卡尔坐标系的笛卡尔不仅是一位伟大的数学家，同时也是一位音乐天才。笛卡尔曾说过：“音乐之美就是数学之美。”他在寻找数学中的灵感时，将自己的想法融入音乐，音乐与数学相得益彰，给了他无数启发。

音乐是感性的美，数学是理性的美。但无形中，二者又彼此纠缠，看似不同，实际密切联系。为了体验它们的魅力，人们在数学和音乐的世界里不断探索。