抽水蓄能发电对直流受端多态频率稳定的影响
王作家,竺炜,程志勇
抽水蓄能发电对直流受端多态频率稳定的影响
王作家,竺炜*,程志勇
(长沙理工大学电气与信息工程学院,湖南省 长沙市 410004)
为了应对直流受端多态频率稳定问题,利用暂、动、静态频率稳定性的性能指标,即瞬间变化率的倒数、阻尼比和静态偏差量的倒数,研究了有无抽水蓄能发电时等值机惯性时间常数和静特性系数的变化;分析了抽水蓄能发电后对暂、动、静态频率稳定性的影响,得出各状态的性能指标并与之前相比较。最后,搭建模型进行仿真。通过理论分析得出,抽水蓄能发电提高了直流受端电网的暂、动和静态频率稳定性,算例仿真验证了理论分析的正确性。研究结果为抽水蓄能发电对直流受端电网多态频率稳定性的影响提供了重要的理论依据。
抽水蓄能;直流接入;暂-动-静态频率稳定性;性能指标
0 引言
由于我国能源和经济的不对称分布,所以采用远距离输电可以优化资源配置,保护自然环境,符合国家的能源发展战略[1]。特高压直流输电在这方面具有显著优势[2-3],从能源丰富的西部地区向经济发达的东部地区输电,是实现“西电东送”战略的重要方式[4],且我国已掌握大量800 kV及以下的特高压直流输电工程建设和运行经验[5-6]。昌吉—古泉特高压直流输电工程将直流电压从目前的800kV提升到1100kV,成为目前国际上电压等级最高、容量最大、距离最远的输电工程[7]。随着直流容量占比增加,直流受端电网的转动惯量逐渐减小,受端系统的调节能力也减弱。因此,受端电网易发生频率振荡,随着新能源的接入,直流受端区域频率问题更加严峻[8-10],研究直流受端多态频率稳定性具有重要意义。
文献[11]针对直流受端电网频率安全问题,提出了两段式频率安全紧急控制策略,利用其控制策略来实现故障后系统频率的紧急控制。文献[12]利用ADPSS软件研究了800kV锦苏直流闭锁对受端电网频率稳定性的影响。而文献[13]则是把逆变站模拟成同步发电机,以此来增加受端系统的转动惯量,但该方法只是提高了受端电网的暂态频率稳定性,并未改善其动、静态频率稳定性。
目前,随着乌东德直流输电工程的馈入,广东电网已通过9回直流馈入“西电”,且落点集中于珠江三角洲区域,但多直流换相失败、频率波动问题突出。针对这些问题,文献[14-15]详细研究了直流输电故障对受端广东电网频率稳定性的影响。文献[16]则针对多直流接入的广东电网,分析其面临的主要问题,并提出了合理化建议。文献[17-18]分析了直流换相失败对受端广东电网的影响。
以上文献基本是从直流故障或频率控制方面阐述了对受端电网的影响,且并未探究受端电网发生频率振荡的根本原因。文献[19]详细研究了影响受端电网多态频率稳定性的因素,推导出相关的主导因子,并提出了其机组的控制策略。本文在文献[19]的基础上,利用其得到的性能指标,研究了抽水蓄能发电对受端多态频率稳定性的影响,为提高频率稳定性提供重要的理论依据。
1 抽水蓄能发电后的等值机惯量及静特性系数变化
目前,电网中扰动频发,由于机组转子具有惯性,频率变化不大,但其变化过程经历暂态、动态和静态。其直流受端区域暂态、动态、静态频率波动过程如图1所示。可用性能指标来定义频率波动过程中暂态、动态、静态的变化过程,3种状态定义的指标如表1所示。
设受端区域有台机组,接入恒功率直流,替换其中台机组,但区域总额定有功容量不变。则直流接入比为

图1 暂、动、静频率波动过程

表1 暂、动、静态频率稳定性指标
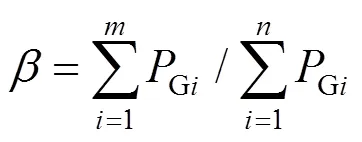
此时等值机的惯性时间常数及功-频静特性系数分别为

若受端区域各机组的惯性时间常数及功-频静特性系数基本一致,则式(2)可表示为


由式(3)和式(4)可知,抽水蓄能发电后,其受端区域等值机的惯性时间常数和功-频静特性系数都增大。
2 抽水蓄能发电对直流受端系统的动态频率特性分析
2.1 基于简单模型的动态频率特性分析
当抽水蓄能未发电时,若区域等值机组以频率反馈调速方式进行控制,则频率反馈简单模型如 图2所示。

图2 抽水蓄能未发电时的频率反馈简单模型

式(5)进行拉氏变换后,可得抽水蓄能发电前的区域功-频开环函数为



故抽水蓄能发电前的动态频率阻尼比为

若抽水蓄能接入发电后,其频率反馈简单模型如图3所示。则其频率响应为

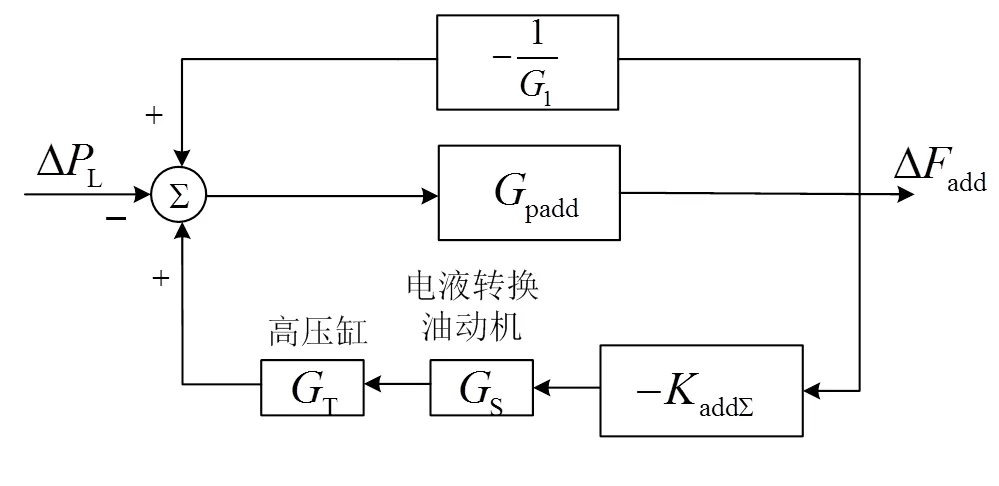
图3 抽水蓄能发电时的频率反馈简单模型
其中





由此可得抽水蓄能发电后的动态阻尼比为



图4 阻尼比比值变化
2.2 基于典型模型的动态频率特性分析
目前国内汽轮机组一般都采用功-频反馈调节,由于机械功率测量困难,功率反馈量一般取自机端电功率(有功功率)。在动态分析时,功率反馈通道实为前馈通道,将负荷扰动前馈量引入控制系统中[21]。功频调节的典型模型如图5所示。

图5 抽水蓄能未发电时的功频反馈典型模型
由图5可得,当该区域等值机组采用功–频反馈调节方式进行控制时,抽水蓄能发电前的区域频率的动态响应为
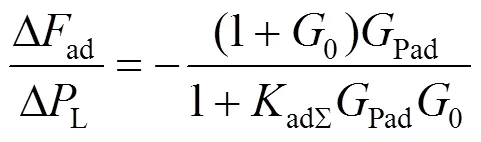
其中
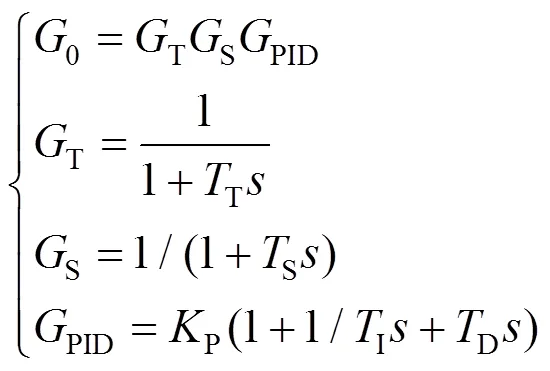


故抽水蓄能发电前的动态频率阻尼比为

当抽水蓄能发电后,其典型模型如图6所示。

图6 抽水蓄能发电时的功频反馈典型模型
其频率响应为

同理,需要对式(21)进行降阶,则式(21)可 写成

由此可得抽水蓄能发电后的动态频率响应为

故抽水蓄能发电后的动态阻尼比为

由式(20)、(24)可得

由式(25)可知,其结果与式(16)相同,由此可表明,无论是基于频率反馈简单模型,还是基于 功-频反馈调节的典型模型,抽水蓄能发电后,其动态稳定性都比抽水蓄能发电前好。
3 抽水蓄能发电对直流受端系统的暂态频率特性分析
3.1 基于简单模型的暂态频率特性分析


若抽水蓄能发电后,此时的频率响应为

则抽水蓄能发电后的瞬间频率波动率为

由式(26)、(28)可得

即抽水蓄能发电后,基于简单模型的暂态频率稳定性变好。
3.2 基于典型模型的暂态频率特性分析
若等值机组以功-频反馈调速方式进行调节,其频率反馈通道不通,则功率反馈成为扰动前馈量。由图4可得

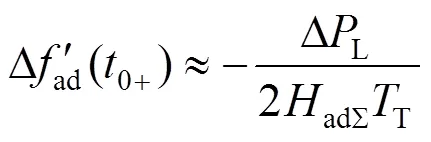
当抽水蓄能发电后,其由负荷扰动引起的瞬间频率波动率为

由式(31)、(32)可得

由此可见,抽水蓄能发电后,基于典型模型的暂态频率稳定性也是变好的。
4 抽水蓄能发电对直流受端系统的静态频率特性分析
4.1 基于简单模型的静态频率特性分析
若受端区域的等值机组采用频率反馈调节方式,则在阶跃负荷扰动下,应用终值定理,受端区域抽水蓄能发电前的稳态频率降为

当抽水蓄能发电后,则在阶跃负荷扰动下,应用终值定理,则受端区域的稳态频率降为

故可得

即抽水蓄能发电后,基于简单模型的静态频率稳定性变好。
4.2 基于典型模型的静态频率特性分析
若受端区域的等值机采用功-频率反馈调节方式,则在阶跃负荷扰动下,应用终值定理,则抽水蓄能发电前的稳态频率降为

当抽水蓄能发电后,则受端区域稳态频率降为

故可得

由此可见,抽水蓄能发电后,基于典型模型的静态频率稳定性也是变好的。
5 基于抽水蓄能发电前后的典型模型时域频率特性仿真分析
设受端区域的调速系统详细模型如图7所示,其中PID=8+0.4/+200/(+200),max=0.7,1= 0.02 s,e=0.05 s,S=0.3 s。

图7 功频调速器模型
当抽水蓄能接入12%及15%时,并采用如图6所示的控制方式,则负荷扰动后频率曲线如图8所示。

图8 抽水蓄能发电前后的多态频率特性图
由图8可知,与未接入抽水蓄能相比,当抽水蓄能接入发电时:
1)频率波动变小,说明暂态稳定性变好。
2)振荡过程中,曲线波动较小,振荡时间变短,说明动态稳定性变好。
3)振荡结束后,频率偏差变小,说明静态稳定性变好。
4)随着抽水蓄能接入比例的增大,多态频率稳定性变好。
6 结论
通过动态、暂态、静态稳定性的性能指标,即阻尼比、瞬间变化率的倒数和静态偏差量的倒数,分析了有抽水蓄能发电和无抽水蓄能发电时,在电网侧扰动下,直流受端区域频率的多态稳定性变化情况。研究发现,抽水蓄能发电后,其暂态、动态、静态频率稳定性比无抽水蓄能时都变好,且抽水蓄能接入比越大,其效果越好,理论和仿真验证了其有效性。
研究结果给抽水蓄能发电接入直流受端区域提供了理论依据,对提高直流受端区域频率稳定性具有重要意义。
[1] 刘振亚.特高压直流输电理论[M].北京:中国电力出版社,2009:5-10.
Liu Z Y.Ultra high voltage direct current transmission theory[M].Beijing,China:China Electric Power Press,2019:5-10.
[2] 孔祥平,李鹏,高磊,等.基于深度学习的特高压直流控制保护系统可视化技术[J].电网与清洁能源,2020,36(2):29-37.
Kong X P,Li P,Gao L,et al.The visualization technology of the UHVDC control and protection system based on deep learning[J].Power System and Clean Energy,2020,36(2):29-37.
[3] 李英彪,梁军,吴广禄,等.多电压等级直流电力系统发展与挑战[J].发电技术,2018,39(2):118-128.
Li Y B,Liang J,Wu G L,et al.Development and challenge of DC power system with different voltage levels[J].Power Generation Technology,2018,39(2):118-128.
[4] 刘振亚,张启平.国家电网发展模式研究[J].中国电机工程学报,2013,33(7):1-10.
Liu Z Y,Zhang Q P.Study on the development mode of national power grid of China[J].Proceedings of the CSEE,2013,33(7):1-10.
[5] 杨娜,陈煜,潘卓洪,等.准东—皖南±1100 kV特高压直流输电工程受端电网的直流偏磁影响预测及治理[J].电网技术,2018,42(2):380-386.
Yang N,Chen Y,Pan Z H,et al.Influence prediction and suppression research of DC bias in eastern Junggar-southern Anhui±1100kV UHVDC receiving-end grid[J].Power System Technology,2018,42(2):380-386.
[6] 黄方能,张红丽,马骞,等.受端电网特高压直流系统与海上风电交互影响及评价指标[J].广东电力,2019,32(3):96-103.
Huang F N,Zhang H L,Ma Q,et al.Interactive effects between HVDC of receiving-end power grid and offshore wind power and evaluation index[J].Guangdong Electric Power,2019,32(3):96-103.
[7] 沈郁,熊永新,姚伟,等.±1100kV特高压直流输电受端接入方式的综合评估[J].电力自动化设备,2018,38(8):195-202.
Shen Y,Xiong Y X,Yao W,et al.Comprehensive evaluation of±1100kV UHVDC transmission receiving end access mode[J].Electric Power Automation Equipment,2018,38(8):195-202.
[8] 文贤馗,张世海,邓彤天,等.大容量电力储能调峰调频性能综述[J].发电技术,2018,39(6):487-492.
Wen X K,Zhang S H,Deng T T,et al.A summary of large capacity power energy storage peak regulation and frequency adjustment performance[J].Power Generation Technology,2018,39(6):487-492.
[9] 林琳,吴星昂,於国芳,等.平抑风电功率波动及负荷调峰的VRB储能应用[J].浙江电力,2019,38(5):25-30.
Lin L,Wu X A,Yu G F,et al.VRB energy storage application for wind power fluctuation suppression and load peak regulation[J].Zhejiang Electric Power,2019,38(5):25-30.
[10] 傅旭,赵娟,张更贺,等.风电场接入对送端电网暂态特性的影响研究[J].分布式能源,2019,4(1):17-21.
Fu X,Zhao J,Zhang G H,et al.Influence of wind power generation on transient characteristics of sending-end power grid[J].Distributed Energy,2019,4(1):17-21.
[11] 李碧君,李兆伟,吴雪莲,等.多直流馈入受端电网两段式频率安全紧急控制策略研究[J].中国电力,2017,50(2):169-174.
Li B J,Li Z W,Wu X L,et al.Research on two-stage frequency security emergency control strategy of multi-DC feeding[J].Electric Power,2017,50(2):169-174.
[12] 卫鹏,周前,汪成根,等.±800 kV锦苏特高压直流双极闭锁对江苏电网受端系统稳定性的影响[J].电力建设,2013,34(10):1-5.
Wei P,Zhou Q,Wang C G,et al.Impact of bipolar in±800 kV Jinsu grid’s receiving-end system[J].Electric Power Construction,2013,34(10):1-5.
[13] 唐欣,张武其,陈胜,等.与VSC-HVDC连接的弱电网暂态频率偏移定量计算和调整方法[J].中国电机工程学报,2015,35(9):2170-2176.
Tang X,Zhang W Q,Chen S,et al.Assessment and regulation of transient frequency deviation in weak grid connected to VSC-HVDC[J].Proceedings of the CSEE,2015,35(9):2170-2176.
[14] 孙景强,郭小江,张健,等.多馈入直流输电系统受端电网动态特性[J].电网技术,2009,33(4):57-60.
Sun J Q,Guo X J,Zhang J,et al.Dynamic characteristics of receiving-end of multi-infeed HVDC power transmission system[J].Power System Technology,2009,34(4):57-60.
[15] 高超,杨雄平,向丽玲,等.大容量多馈入直流对广东电网运行稳定性影响的研究[J].广东电力,2010,23(7):22-26.
Gao C,Yang X P,Xiang L L,et al.Research on impact of multi-infeed HVDC on stability of Guangdong power grid[J].Guangdong Electric Power,2010,23(7):22-26.
[16] 张东辉.多直流集中馈入受端广东电网发展的思考[J].广东电力,2015,28(8):33-37.
Zhang D H.Reflect on development of centralized feed-in of multi direct current into receiving-end Guangdong power grid[J].Guangdong Electric Power,2015,28(8):33-37.
[17] 周保荣,洪潮,饶宏,等.广东多直流输电换相失败对电网稳定运行的影响[J].南方电网技术,2017,30(3):23-29.
Zhou B R,Hong C,Rao H,et al.Influence of simultaneous commutation failure of Guangdong multiple HVDC on power system secure operation [J].Southern Power System Technology,2017,30(3):18-24.
[18] 赵利刚,赵勇,洪潮,等.基于实际录波的南方电网多回直流换相失败分析[J].南方电网技术,2014,8(4):42-46.
Zhao L G,Zhao Y,Hong C,et al.Analysis on commutation failure of the CSG’s HVDC systems based on actual waves[J].Southern Power System Technology,2014,8(4):42-46.
[19] 竺炜,钟鹏,巫晓云.直流接入后的多态频率稳定性及机组控制策略[J].中国电机工程学报,2016,36(22):6122-6130.
Zhu W,Zhong P,Wu X Y.Multi-state frequency stability and power unit control strategy after DC access[J].Proceedings of the CSEE,2016,36(22):6122-6130.
[20] 魏守平.水轮机调节系统的MATLAB仿真模型[J].水电自动化与大坝监测,2009,33(4):7-11.
Wei S P.MATLAB simulation model of hydraulic turbine regulating system[J].Hydropower Automation and Dam Monitoring,2009,33(4):7-11.
[21] 竺炜,周有庆,谭喜意,等.电网侧扰动引起共振型低频振荡的机制分析[J].中国电机工程学报,2009,29(25):37-42.
Zhu W,Zhou Y Q,Tan X Y,et al.Mechanism analysis of resonance-type low-frequency oscillation caused by networks side disturbance[J].Proceedings of the CSEE,2009,29(25):37-42.
Influence of Pumped Storage Power Generation on Multi-state Frequency Stability of DC Receiver
WANG Zuojia, ZHU Wei*, CHENG Zhiyong
(School of Electrical and Information Engineering, Changsha University of Science&Technology,Changsha 410004, Hunan Province, China)
In order to deal with the problem of multi-state frequency stability at DC receiving end, this paper studied the variation of inertia time constant and static characteristic coefficient of equivalent machine with or without pumped storage power generation by using the performance indexes of transient, dynamic and static frequency stability, namely reciprocal of instantaneous change rate, damping ratio and reciprocal of static deviation. The influence of pumped storage power generation on transient, dynamic and static frequency stability was analyzed. The performance indexes of each state were obtained and compared with those before. Finally, the model was built for simulation. Through theoretical analysis, it is concluded that pumped storage power generation improves the transient, dynamic and static frequency stability of the DC receiving end power grid. The correctness of theoretical analysis was verified by numerical simulation. The research results provid an important theoretical basis for the influence of pumped storage power generation on the multi-state frequency stability of DC receiving end power grid.
pumped storage; DC access; temporary-dynamic-static frequency stability; performance index
10.12096/j.2096-4528.pgt.19038
TM 612
2019-03-25。
(责任编辑 辛培裕)

