闭链双模式多足平台的设计与研究

武可庚 ，翟美丽

(1．太原铁路机械学校，山西 太原 030006)

(2．北京师范大学附属中学，北京 100052)

地面移动平台按照移动方式可以分为轮式、履带式和腿式平台[1-3]。其中，轮式平台在平坦路面速度快、机动灵活、移动效率高；履带式平台在复杂环境下接地比压小、载荷能力强、越障能力良好；腿式平台相较于轮式和履带式平台具有最为突出的地形适应能力，可代替人类广泛应用于工业、探险、医疗、军事等领域。

现有的腿式移动平台多为开链式结构，从仿生学的角度展开设计，驱动电机直接安装于关节处，开链式腿平台具有灵活的腿部运动和动态特性。波士顿动力公司以开链式结构研发了6款平台：BigDog，LittleDog，LS3，WildCat，Spot和SpotMini[4]，通过多电机协同控制和多传感器融合实现丰富的步态，具备良好的动态稳定性和地形通过性。为获得高速移动性能,麻省理工学院先后研制了三代Cheetah平台[5]。意大利技术研究所研制了两代HyQ[6]平台，显著提升了腿式平台的任务可靠性、躯干灵活度和电机输出力矩。

开链腿机构研究广泛，同时也受到肢体动载荷、运动感知精度、动力能源系统质量与控制系统复杂度的限制。相比较而言，闭链腿机构多为曲柄驱动的单自由度闭链机构，以多连杆耦合连接代替开链腿机构的多电机协同控制；以整周旋转驱动曲柄代替往复摆动驱动关节；以闭链高刚度自稳定结构代替串联式结构。闭链腿机构包含3种经典机构，即Chebyshev腿机构、Jansen腿机构、Klann腿机构[7]。我国学者着眼于闭链腿机构单动力可靠性，系统地开展了古军事装置“木牛流马”的复原设计[8]。闭链腿机构通过曲柄高频转动实现腿式平台高速移动，Park等[9-10]通过高速曲柄旋转分别实现了水上与陆地奔跑。

面向闭链腿机构的单动力、高频率和高刚度特性，本文提出一种兼具上肢和下肢的新型单动力十连杆闭链腿机构，并开展了多足模块和行走底盘的集成，整机以二十四足的形式实现正反双模式行走运动。

1 构型创新设计

1.1 闭链腿机构设计

目前，腿式平台若采用开链腿机构，存在着以下限制条件：1)多个驱动分别安装在开链腿机构关节位置，增加了整备质量和行走能耗；同时下级驱动成为上级驱动的负载，增大了上级驱动能力的要求。2)开链腿机构刚度较小，难以承担载质量大的工作。3)为产生平顺步态，需要多传感器和执行器协同，增加了控制复杂程度。相比较而言，闭链腿机构为单自由度连杆结构，采用曲柄的整周旋转的方式输出周期性步态；闭链腿机构以机械相位的协调配置取代了多电机的同步控制，降低了整机质量和控制系统复杂度；同时闭链机构具备更大的承载能力和整体刚度。

由此，本文设计新型单自由度闭链腿机构，进一步构造四足模块和多足行走底盘，充分发挥闭式运动链机构特性与优势：单动力闭链腿机构面向山地等复杂环境的作业需求，可有效减少整机行走驱动、运动控制器和传感器数量，从而提升整机可靠性。同时构造四足模块作为机动单元，便于实现故障隔离，提高维修互换性，减少研发周期与成本。

下面进行单自由度闭链腿机构创新设计[11]，总结现有闭链腿机构拓扑构造的设计约束如下：1)单自由度机构；2)平面低副组成；3)具备曲柄、大腿、小腿和机架特定化杆件；4)大腿杆件与曲柄隔离，大腿杆件与曲柄分别与机架连接；5)小腿杆件与机架隔离；6)足端轨迹为封闭无交叉轨迹曲线。在4杆～10杆的全部可行闭式运动链中，从10杆13副非同构运动链图谱(共包括230种构型)中进行运动链选型并开展机构设计。本文设计(10,13)型运动链，如图1(a)所示；进一步按顺序进行杆件的特定化分配得到对应的特定化链，如图1(b)所示；基于特定化链开展具体化设计，保持邻接关系不变的同时将连杆和运动副转化为构件和运动关节，生成闭链单腿机构，如图1(c)所示；为避免杆件之间形成摩擦甚至干涉，将发生相邻或相交的杆件分层，并采用垫片或推力轴承居间隔离，曲柄与大腿杆件成对布置以保证强度，所设计腿结构共分为8层，分层设计如图1(d)所示。

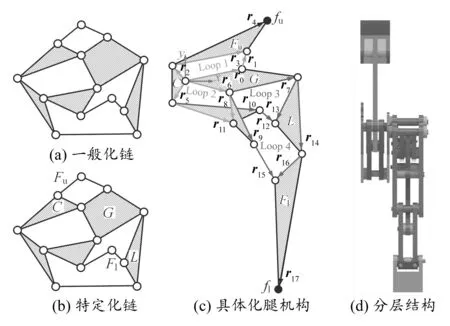
图1 闭链腿机构

所构造的十连杆闭链腿机构，自由度F为：F=3n-2Pl-Ph=1,其中n为活动杆件的数量(n=9)，Pl为低副的数量(Pl=13)，Ph为高副的数量(Ph=0)。所设计单动力闭链腿机构具备上下两套行走执行端，即在正反状态皆可实现行走运动，其足端行走特性分析如下。

1.2 运动学分析

所设计的闭链腿机构，其曲柄整周旋转，分别带动上肢与下肢的大腿、小腿和足端运动，并生成足端轨迹。根据欧拉定理，10杆13副闭链腿机构环路数量L：L=j-n=4，其中j为关节数量。上肢由1个环路组成，下肢由3个环路组成。建立坐标系O-xy，坐标系原点O设置在曲柄与机架杆件的转动中心处，闭环矢量和运动参数标记在图1(c)中。采用矢量环路法对闭链单腿机构进行运动学分析，如式(1)所示，得到足端和关节的运动参数。

loop 1：r0+r1-r3-r2=0

loop 2：r6+r8-r11-r5=0

loop 3：r6+r7+r13-r12-r10-r5=0

loop 4：r7+r14+r16-r15-r9=0

(1)

点u与点l分别为两种状态下的足端(fu,fl)输出，足端位置参量ru，rl可表示为:

ru=rl+r4

(2)

rl=r1+r2+r6+r9

(3)

矢量环路法得到的下肢与上肢足端运动轨迹如图2所示。空转状态下对应曲柄转速为180 r/min，单周期内，下肢足端运动速度在-1 265～2 136 mm/s内波动，上肢足端运动速度在-1 949 ～1 016 mm/s内波动。

图2 足端运动学特性

2 底盘特性分析

2.1 行走底盘布局

基于十连杆闭链腿机构，逐级分层构造得到单动力六足单元和四驱动行走底盘，极大程度缩减了驱动电机数量、降低了整机质量并简化了控制系统的复杂程度；所构造行走底盘为二十四足布局形式(正面为十六足、反面为八足)，多个闭链腿机构共同支撑增加了整机载重/自重比；行走底盘的24个闭链腿机构由4个减速电机带动曲柄整周旋转驱动，避免了电动推杆(或液压推杆)驱动腿部运动需频繁地换向而产生的行走能耗，相比较而言，转动驱动易于提升行走效率和移动步频。

首先，构造单动力六足单元：六足单元的布局方式如图3(a)所示，前后双腿采用外膝肘式，增大躯干下侧空间与支撑面积。在单动力六足单元中，前侧采用具有四环路(loop 1～loop 4)的十连杆腿机构，后侧采用具有三环路(loop 2～loop 4)的八连杆腿机构。通过耦合曲柄和机架杆件，将曲柄相位差设置为π，并由一个减速电机驱动行走。

然后，集成行走底盘：行走底盘的布局方式如图3(b)所示，六足单元以4×4阵列布局于机身，同时整机分布4个减速电机,分别用于4个六足单元的独立驱动。行走底盘中部为载物仓，用以存放货物，整机布局沿着纵向中心面左右对称。正面行走时，行走底盘为十六足机构；若发生倾覆或反面行走时，行走底盘为八足机构。

图3 行走底盘布局

2.2 步态特性比较

所构造的多足行走底盘在正面和反面两种模式下具有不同的行走特性：首先，两种模式下具备不同的支撑单腿机构构型,正面模式下为三环路的八连杆腿机构支撑，反面模式下为单环路的四连杆腿机构支撑。其次，两种模式下具备不同的支撑腿数量,正面模式下为十六足共同支撑行走，反面模式下为八足共同支撑行走。

将正面、反面的支撑腿以四足为单元进行标号：正面(z1,z2,z3,z4)，反面(f1,f2,f3,f4)，如图3(b)所示。基于MATLAB对两套足端轨迹进行数值分析，在直行状态下，行走底盘的4个六足单元均为同步运动，如图4(a)所示为正面模式下支撑步态序列，单腿支撑相(阴影部分)位于区间[1.00π，1.50π]；如图4(b)所示为反面模式下支撑步态序列，单腿支撑相(阴影部分)位于区间[0.74π，1.74π]。

图4 步态分析

因此，正面模式下单腿实现1/4周期支撑，反面模式下单腿实现1/2周期支撑，正面模式的支撑区间相较于反面模式缩小了一半，缩小的单腿支撑相可以使得跨越足落地更加平缓，支撑足的支撑波动值更小，行走更加稳定。通过数值分析测算得到两种模式下的行走参数(相位区间、跨步长度、质心波动、俯仰波动)，见表1。

表1 行走参数比较

3 行走特性分析

对所构造的多足行走底盘进行动力学分析，从闭链腿机构自身特性入手：面向曲柄的高频转动特性，给出六足单元的惯性力分析；面向多闭链腿部支撑的高刚度特性，给出行走底盘的驱动、足端受力和能耗分析；面向行走底盘正反双模式行走特性，给出快速性、灵活性和通过性等机动性能分析比较。搭建ADAMS动力学仿真模型，具体参数见表2。

表2 仿真参数设定

高频旋转驱动惯性力分析：闭链腿机构通过曲柄的高速旋转驱动腿部高频往复摆动，从而蹬地产生推进力。将行走驱动的转动频率设置为3 Hz，将仿真过程设定为2 s共计2 000步，得到台架状态下沿垂向的惯性力在31.18 ～91.98 N内波动，均方根为80.401 5 N；沿纵向的惯性力在-37.27 ～36.47 N内波动，均方根为25.779 5 N；三轴惯性力矩均方根分别为3.47，5.28，1.97 N·m。

进行直线行走的动力学仿真分析，将行走驱动的转动频率设置为1 Hz，将仿真过程设定为3 s共计2 000步，测算两种模式下的行走功耗(图5(a))与行走速度(图5(b))，由图可知，正面模式相较于反面模式具有更高、更平稳的牵引速度。

图5 行走特性分析

最后，对比分析两种模式对应的爬坡性能和转向性能。在仿真环境中搭建20°斜坡开展爬坡测试，爬坡驱动力矩如图6(a)所示，正、反两模式爬坡力矩均方根分别为3.268 和2.683 N·m，峰值力矩分别为13.855 和11.730 N·m，由此可知，正面模式对电机的驱动需求更高。爬坡状态下后腿的受力如图6(b)所示，正面模式由多足支撑牵引，爬坡过程受力工况更好。

图6 爬坡特性分析

无论是正面模式还是反面模式，行走底盘均在差速驱动下实现转向，将左右两侧闭链腿机构的转动速度分别设置为60 和-60 r/min，进行原地转向的动力学分析。图7(a)所示为两模式的转向扭矩，测算得到正、反两模式原地转向峰值力矩分别为8.38 和8.86 N·m，均方根分别为3.29 和3.26 N·m。图7(b)所示为原地转向角速度，测算得到正、反两模式转向平均角速度分别为31.66 和13.08 (°)/s，从而进一步得到2 s原地转向的角位移分别为63.48°和26.21°。正、反两模式在原地转向工况对电机输出需求相差不大，而正面模式的转向性能更好，具有更为灵活的转向能力。

图7 转向特性分析

4 结束语

本文提出一种新型的单自由度十连杆闭链腿机构，兼具上肢与下肢两套足端，上、下足端可以同时输出行走运动。在闭式运动链的基础上进行了特性化配置、具体化设计与腿部杆件结构分层，并通过矢量环路法求解得到十连杆闭链腿机构的运动学参量。构造了单动力六足单元和双模式行走底盘，整机采用4个减速电机驱动，实现了正面十六足支撑行走与反面八足支撑行走，两种行走模式具有不同的行走足端轨迹、速度特性和运动步态，本文进行了双模式步态分析和行走参数比较。建立了多足行走平台的三维模型和动力学仿真环境，针对曲柄高频旋转驱动特性、多闭链耦合支撑牵引特性和双模式行走机动性能开展了动力学仿真分析，通过虚拟样机仿真与原理样机试验，验证了理论分析结果的正确性与多足行走平台的可行性。