人字齿行星减速器膜片式柔性行星架设计与均载特性分析

赵 波，王德伦，董惠敏，邱 俊

(大连理工大学机械工程学院， 辽宁 大连 116024)

人字齿行星齿轮传动，相对于直齿轮传动具有更大的重合度，传动更平稳；相对于斜齿轮传动不会产生附加轴向力，螺旋角可以更大，承载能力更强。在行星传动系统中，由于制造误差、安装误差以及构件弹性变形等因素引起的行星齿轮承载分配不均，导致人字齿行星齿轮承载的优点难以发挥出来，因此研究行星齿轮的均载特性，对于改善系统工作性能、提高承载能力有重要意义。

国内外众多学者对行星齿轮的均载特性进行了多方面的研究。Singh[1]给出了计算均载系数的通用公式。任菲[2]研究了制造、安装误差对人字齿行星齿轮均载特性的影响。李阳等[3]分析了具有间隙浮动机构的行星轮系静力学均载问题。巫世晶等[4]研究了啮合误差对行星轮系动态均载特性的影响。Kahraman[5]综合考虑啮合间隙、制造误差、安装误差、啮合刚度的变化对行星齿轮均载性能的影响。张霖霖等[6]进行了啮合相位对人字齿行星齿轮传动系统特性的影响研究。在弹性变形方面，徐向阳等[7]研究了柔性销轴对齿轮箱均载性能的影响。

本文针对两级人字齿行星减速器设计了一种新型膜片式柔性行星架，利用ADAMS软件建立减速器动力学模型，验证膜片式柔性行星架对行星传动系统均载性能的影响。

1 膜片式柔性行星架设计

本文研究对象为两级NGW型渐开线人字齿行星减速器,机构简图如图1所示，额定输出扭矩为400 N·m，电机输入转速为100 r/min，齿轮参数见表1。

图1 人字齿行星减速器机构简图

表1 减速器各齿轮参数

为提高行星齿轮的均载性能，美国齿轮制造协会在6123—B—2006[8]标准中提出了19种方法，可以归结为： 1)提高构件制造安装精度； 2)一个或多个构件径向浮动； 3)一个或多个构件的弹性变形。其中构件的弹性变形包括齿圈或太阳轮单一构件的弹性变形、齿圈与太阳轮两者同时弹性变形、行星齿轮支撑轴的弹性变形、行星架的弹性变形。减速器原方案中行星架为刚性行星架，本文设计一种新型的柔性行星架，将现有的刚性行星架设计成膜片形式，每层膜片之间以垫片相隔，从而增加其弹性变形能力，如图2所示。

图2 原方案行星架与膜片式柔性行星架

为了使行星架具有传递扭矩和运动的功能以及较大的轴向变形能力，要求柔性行星架具有较大的周向刚度和较小的轴向刚度。对不同膜片厚度、不同膜片数量的设计方案进行有限元分析。将带有行星轮轴的行星架模型导入ANSYS有限元软件，对行星架中心质量点与行星架花键区域施加耦合，添加扭矩，以此模拟行星轮系的负载，根据减速器额定运行工况，第一级输出扭矩约为80 N·m；对行星轮轴与转臂轴承接触区域施加约束，模拟转臂轴承对行星轮轴的支撑作用，生成有限元模型，如图3所示。

图3 行星架有限元模型

求解有限元模型，分别提取代表行星架轴向、周向刚度的轴向和扭转方向变形结果如图4所示，得到不同膜片厚度、不同膜片数量的行星架最大变形结果见表2。

图4 行星架扭转方向和轴向位移云图

表2 不同膜片厚度、不同膜片数量的行星架最大变形 mm

比较表2中轴向和周向变形，在相同工况下，为满足轴向尺寸要求，选用3片0.75 mm膜片的行星架方案。

2 人字齿行星减速器动力学仿真

2.1 建立三维实体模型

利用CREO2.0三维建模软件建立两级行星轮系各个零件的实体模型，并对不同的行星架进行装配，两级人字齿行星减速器装配体三维结构模型如图5所示。

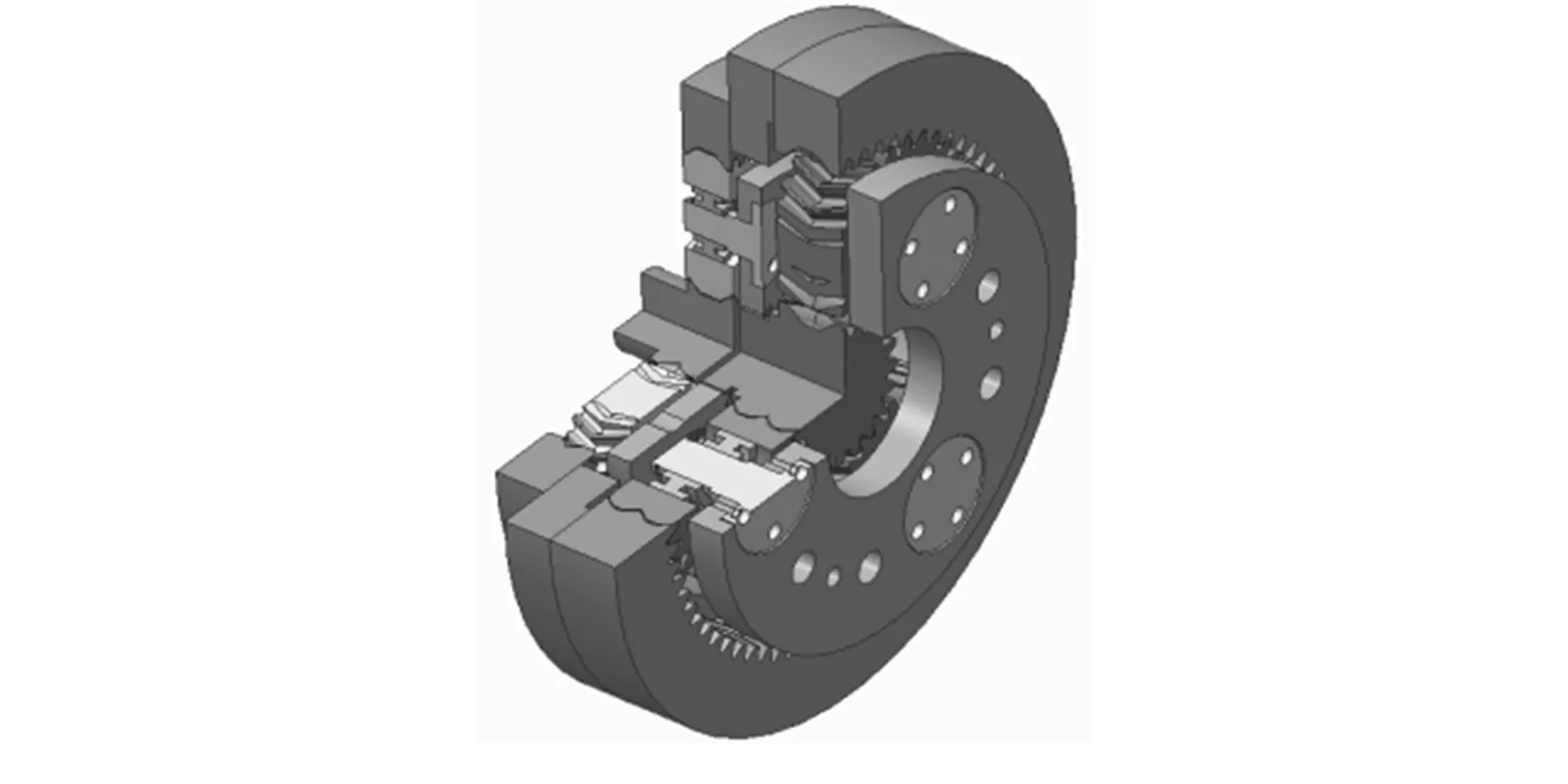
图5 两级人字齿行星减速器装配体三维结构模型

2.2 动力学仿真模型

根据减速器的运动规律，在减速器联接构件间施加转动副、固定副、接触力等约束。两级人字齿行星减速器由第一级行星轮系的太阳轮输入额定转速，第二级行星轮系的行星架实现扭矩和运动的输出，第一级行星架与第二级太阳轮以花键连接，实现两级之间扭矩和运动的传递，行星轮轴与行星轮之间以转臂轴承相连，行星轮与行星轮轴只有相对转动。在动力学模型中，对第一级太阳轮施加额定转速以模拟传动系统中电机的输入；内齿圈与地面施加固定约束，模拟机架对减速器的支撑；行星轮轴与行星轮之间建立转动副；本文不考虑花键配合间隙对柔性行星架的影响，内外花键以固定副连接；在相互啮合的齿轮之间施加接触力，建立动力学仿真模型如图6所示。

图6 减速器动力学模型

2.3 齿轮接触载荷参数设置

ADAMS软件中对接触力的求解方法有两种：一种是基于赫兹接触理论的冲击函数法，一种是补偿法。由于补偿法中的惩罚系数和补偿系数很难准确确定，因此本文采用冲击函数法。

冲击函数模型法向接触力表达式为：

(1)

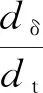
切向接触力方向与相对滑移速度方向相反，大小与正压力成正比，函数表达式为：

Fs=-Fn×step(vt,-Vs,-1,Vs,1)×step(ABS(vt),Vs,fst,Vd,fdy)

(2)

式中：Fs为切向接触力；vt为轮齿相对滑移速度；ABS()为绝对值函数；fdy为动摩擦系数；fst为静摩擦系数；Vd为动摩擦相对滑移速度；Vs为静摩擦相对滑移速度。

ADAMS软件中接触载荷的相关参数主要由相接触的材料属性与边界条件确定，依据文献[9]、[10]确定具体参数。

接触刚度系数K：

(3)

其中：

(4)

式中：R1，R2分别为两实体在接触点的当量曲率半径；E1，E2为相互啮合齿轮的弹性模量；ν1，ν2为相互啮合齿轮的泊松比。对于斜齿轮，需要计算其法面曲率半径Rn：

(5)

式中：d1，d2为齿轮分度圆直径；αt为齿轮副啮合压力角;βb为齿轮螺旋角。本文齿轮材料为18CrNiMo7-6，取用弹性模量E=2.07E+05 MPa,泊松比ν=0.27。

由式(3)～式(5)计算可得：

第一级太阳轮-行星轮接触刚度系数K=3.052 1×105；行星轮-内齿圈接触刚度系数K=5.472 3×105。

第二级太阳轮-行星轮接触刚度系数K=3.430 2×105；行星轮-内齿圈接触刚度系数K=3.908 9×105。

接触阻尼系数C取40;非线性弹簧力系数e取1.5;最大穿透深度dmax取为0.1 mm;动摩擦系数fdy为0.05；静摩擦系数fst为0.08；动摩擦相对滑移速度Vd为10 mm/s；静摩擦相对滑移速度Vs为0.1 mm/s。

2.4 行星轮系刚柔耦合模型建立

ADAMS软件中建立柔性体的方法主要有两种：一是利用ADAMS中Rigid to Flex功能将已有刚性体模型转换为柔性体；另一种是利用有限元分析软件生成mnf文件(模态中性文件)，该方法不需要产生中间数据，可用于形状复杂的零件。本文采用ANSYS有限元分析软件将膜片式行星架进行柔性化，如图7所示。

图7 行星架柔性化

对两种行星架进行模态分析，其结果见表3。

表3 行星架模态分析结果

3 动力学均载特性分析

均载系数是评价传动系统均载性能的重要指标，数值越大表明系统的均载性能越差。在运行时间内行星传动系统的均载系数定义为[11]：

Bspi=max{bspij},Brpi=max{brpij}

(6)

其中：

式中：Frpij和Fspij分别为每个齿频周期内行星传动系统第i个内、外啮合副的动态啮合力；brpij和bspij分别为行星传动系统行星轮在每个齿频周期内的内啮合副与外啮合副的均载系数；Brpi和Bspi分别为行星传动系统行星轮在运行时间内的内啮合副与外啮合副的均载系数；n1和n2分别为运行时间内外啮合副和内啮合副的齿频周期数；N为行星轮个数。

根据减速器的额定工况，在ADAMS中设定输入转速v=600 (°)/s，负载转矩T=4×105N·mm，仿真时长t=15 s，仿真步长step size=0.005。可以得到人字齿行星减速器在运行时间内brpi和bspi变化曲线，如图8所示。

图8 原方案均载系数

采用新型膜片式柔性行星架，系统在同工况下一段时间内的brpi和bspi变化曲线如图9所示。

图9 采用柔性行星架方案均载系数

由图8，9可知，第一级行星轮的内啮合均载系数由1.509 6降低到1.359 8，外啮合均载系数由1.380 4降低到1.215 3。第二级行星轮的内啮合均载系数由1.338 2降低到1.152 6，外啮合均载系数由1.400 1降低到1.133 0。由此可知，行星轮系传动系统采用柔性行星架传递运动，其均载性能得到了明显改善。

4 结束语

本文提出了一种新型的膜片式柔性行星架的设计方案，并进行了不同膜片厚度、不同膜片数量条件下行星架的有限元分析；建立某工况下人字齿行星减速器ADAMS动力学仿真模型，针对原方案行星架减速器与应用新型行星架的减速器进行了刚柔耦合动力学仿真，进行了均载特性分析。

与两级行星传动系统刚性连接相比，采用本文提出的膜片式柔性行星架，提高了中心构件受力后周向变形能力以及系统的均载性能。