订单成本与提前期相关下含次品的集成库存模型*

□ 朱心怡，黄远良

(桂林理工大学 商学院,广西 桂林 541004)

传统的经济订购批量模型假设销售商从供应商订购运输来的产品是完全合格品，然而在实际中由于生产不完美或者运输颠簸等原因会造成订购批量中含有部分次品。Salameh等[1]最早构建了一个订购批量中含有次品的经济订购批量模型，由于Salameh等[1]研究工作的突破性，后来研究者对该模型进行了各个方面的扩展研究。Hsu等[2]研究了允许库存短缺且允许退货下产品检查存在误差的次品经济订购批量模型。Su[3]研究了短缺需求完全拖后下销售商可延期支付货款的次品集成库存模型。Taleizadeh等[4]研究了库存短缺期间顾客需求部分拖后下次品可修复的经济订购批量模型。Tiwari等[5]研究考虑碳排放下同时存在产品变质与产品缺陷的库存模型。Chen等[6]研究了库存短缺下部分需求可用其他产品替代的次品库存模型。

以上研究次品库存的文献均假设订货提前期为零，然而在实际中从销售商发出订货申请到产品运输到达销售商库存中需要一定的时间，这段提前期可长可短，但可以通过业务流程重组等方法来压缩提前期。Sarkar等[7]研究了延期支付下提前期可压缩的次品集成库存模型。黄远良等[8]研究了库存短缺下订购批量采用抽检方式且提前期与丢单率相关的次品库存模型。Das等[9]研究了销售商的延期支付货款期限依赖次品率的集成生产库存模型。Priyan等[10]研究了延期支付下通过投资降低订购成本且给予等待顾客一定的价格折扣的次品集成库存模型。Tiwari等[11]研究了库存短缺下通过投资降低生产启动成本且给予等待顾客一定的价格折扣的次品集成库存模型。在文献[11]中订单成本与提前期是相互独立的，然而在实际中使用电子数据交换(EDI)可以同时减小订单成本与提前期，即他们是相关的。故本文将文献[11]进一步推广到订单成本与提前期是相关的情形。

1 符号说明与模型假设

符号说明：D合格品的市场需求率，P供应商产品生产率，S0供应商初始生产启动成本，S供应商投资后的生产启动成本，hb销售商单位时间单位产品的库存持有成本，hv供应商单位时间单位产品的库存持有成本，s产品检查速率，Cs检查成本，C0次品的处理成本，y次品率，Q销售商订购批量，r销售商再订货点，k安全库存因子，L订货提前期，m运输次数，πx拖后价格折扣，A销售商订单成本，μ错误接受次品的成本，μ0错误拒绝合格品的成本，θ单位时间单位资金的机会成本，m1合格品归为次品的概率，m2次品归为合格品的概率，C(L)提前期赶工成本，β需求拖后率，β0最大的拖后折扣，π0边际毛利润，σ提前期内需求标准差。

2 模型构建

2.1 销售商单位时间成本

销售商每次向供应商发出的订购批量为Q，而供应商每次生产mQ批量的产品，并分m次等批量运输到销售商处。由于生产不完美或者运输颠簸等因素，销售商接收到的订购批量Q中含有部分次品，次品率y是一个随机变量。销售商对全批量进行检查，而批量检查也存在误差，即把合格品归为次品(Ⅰ型误差)与次品归为合格品(Ⅱ型误差)，最后，实际的次品率为ye=(1-y)m1+(1-m2)y。记其期望为Ye=E[ye]=(1-E[y])E[m1]+(1-E[m2])E[y]，那么销售商期望订购周期为Q(1-Ye)/D。

销售商单位时间成本包括订单成本、合格品与次品库存持有成本、拖后成本、误差成本、检查成本、提前期赶工成本与次品处理成本，即

(1)

2.2 供应商单位时间成本

供应商单位时间成本包括投资降低生产启动成本的费用、生产启动成本与库存持有成本，即[11]

(2)

综合以上分析可得到由单一供应商与单一销售商组成的集成库存成本模型

(3)

(4)

当订单成本与提前期无关时本文模型(4)式就退化为文献[11]的模型，即本文模型是文献[11]的推广。

3 模型分析

命题1 给定Q、S、k、πx与m，集成库存成本函数JETCU是关于L的凹函数。

证明：求JETCU关于L的一阶、二阶偏导数，得到

(5)

(6)

命题2 给定S、k、πx、L与m，集成库存成本函数JETCU是关于Q的凸函数。

证明：求JETCU关于Q的一阶、二阶偏导数，得到

(7)

(8)

(9)

那么最优的Q*要满足(9)式。

命题3 给定Q、S、πx、L与m，集成库存成本函数JETCU是关于k的凸函数。

证明：求JETCU关于k的一阶、二阶偏导数，得到

(10)

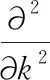
(11)

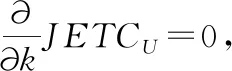
(12)

那么最优的k*要满足(12)式。

命题4 给定Q、S、k、L与m，集成库存成本函数JETCU是关于πx的凸函数。

证明：求JETCU关于πx的一阶、二阶偏导数，得到

(13)

(14)

(15)

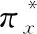
命题5 给定Q、k、πx、L与m，集成库存成本函数JETCU是关于S的凸函数。

证明：求JETEU关于S的一阶、二阶偏导数，得到

(16)

(17)

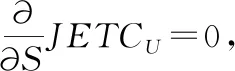
(18)

那么最优的S*要满足(18)式。

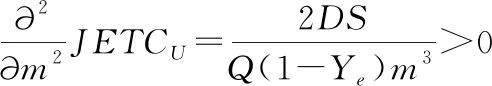
算法：

步骤1 令m=1,j=1。

步骤2 对每个Li，i=1,…,n；

2a令kj=0，πxj=0，Sj=S0；

2b把kj、πxj与Sj代入(9)式，计算得到Qj；

2c把Qi与πxj代入(12)式，计算得到kj+1；

2d把Qj代入(15)式，计算得到πxj+1；

2e把Qj代入(18)式，计算得到Sj+1；

2f把πxj+1、Sj+1与kj+1代入(9)式，计算得到Qj+1；

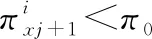
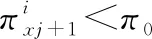
步骤6 若JETC(Q(m),k(m),πx(m),S(m),L(m),m)≤JETC(Q(m-1),k(m-1),πx(m-1),S(m-1),L(m-1),m-1)，则令m=m+1返回步骤2，否则转到步骤7；

4 算例分析

表1 赶工成本与提前期的关系

表2 最优解的计算过程

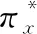
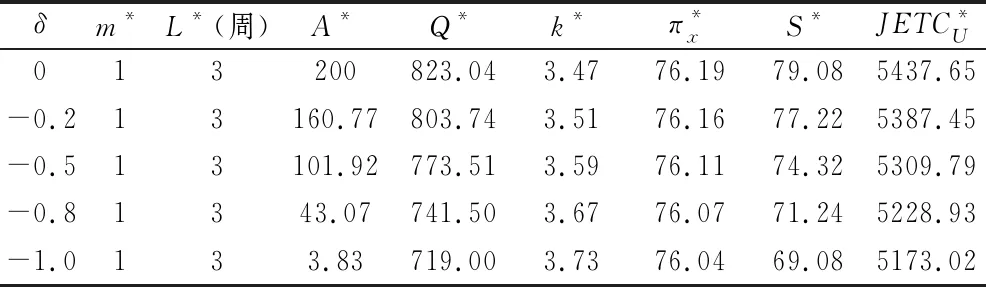
表3 参数对库存系统的影响

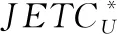
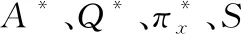
表4 初始订单成本对库存系统的影响

5 结束语

本文研究了销售商订单成本与提前期相关下存在产品检查误差的次品集成库存模型，其中，供应商通过投资来降低生产启动成本，而销售商允许库存短缺，在库存短缺期间给予顾客一定的价格折扣，但对提前期需求仅知道其均值与方差。文章在构建相应的模型之后对其进行了分析，给出了5个命题，并设计一个算法求解最优解。最后，考察主要参数对库存系统的影响。结果显示，当考虑销售商订单成本与提前期相关时集成库存成本会降低。本文可进一步推广到延期支付货款、动态定价等情形。