通过区域筛选和简洁de Bruijn图比对高重复短序列
黎 瑶,钟 诚
(广西大学 计算机与电子信息学院 广西高校并行分布式计算技术重点实验室,南宁 530004)
E-mail:1176423710@qq.com
1 引 言
序列比对是生物大数据分析应用中的基础性工作,有利于后续的基因组信息解读.短序列比对(short-read alignment)是序列比对中的一种,它将测序平台产生的大量的短序列与参考基因组进行对准定位[1].细菌、哺乳动物等物种中存在着许多重复子序列,这给序列比对提出了新的挑战.Illumina机器产生的高通量测序序列相对较短(100~300bp)、错误率相对较低(1%~2%)、但重复率高的特点使得序列在很多位置都将被“匹配”[2].如何找到唯一的最佳匹配相当困难,这使得序列比对更具挑战性.处理高通量测序数据使用的关键数据结构之一是de Bruijn图[3].De Bruijn图在基因组装[4]、转录组装配[5]、宏基因组学[6]、变体识别和结构变异检测[7]、序列比对[8]等领域得到了应用.
已有的大多数序列比对方法都是基于种子-扩展(seed-and-extending)策略进行搜索比对[9-13].基于种子-扩展策略的序列比对主要有4个步骤:种子生成、种子匹配、种子扩展(扩展每个匹配的种子)以及最终对准(测序序列与参考基因组的最终映射定位).基于种子-扩展策略的序列比对面临的主要瓶颈之一是如何处理基因组中的重复区域(例如:人类基因组含有超过50%的重复子序列[14]).当将测序序列(read)与包含许多“重复”区域的参考基因组进行比对时,将会出现许多种子在参考基因组中有多个命中(hit)的情况,从而导致所有种子的扩展计算成本非常高.近几年来,人们提出了启发式的过滤命中[12,15]、限制每个种子的命中数[9,11]、在扩展前合并命中[9-10,13]等策略,以期望有效地处理种子命中.然而,这些策略均是独立地处理每个命中.评估、排序和处理大量命中的成本高.在评估、排序和处理步骤完成之后,由于子序列的重复可能仍有许多候选位置留下来需进行扩展,这导致将大量测序序列与参考基因组每个候选位置逐个对准的成本仍然较高.
为解决大量的种子命中和扩展候选位置代价高的问题,BGREAT[16]和deBGA[17]采用早期停止机制:当种子不匹配的数量超过某个阈值时,则停止探索de Bruijn图的节点.采用此机制可以减少搜索空间,但可能无法返回最佳比对结果.Heydari等人提出一种将大量的短序列与参考基因组生成的de Bruijn图进行比对的算法BrownieAligner[18].该算法计算de Bruijn图的每个分支对准计分上限,直到无法改进目前找到的最佳解决方案时,则丢弃分支.在搜索比对de Bruijn图过程中,BrownieAligner算法采用的深度优先搜索可能无法在找到最佳路径之前访问更多的结点,这将导致正确比对百分比不够高.针对将含有重复子序列的测序短序列与参考基因组进行比对的问题,本文采用基于空位种子查找策略的区域选择方法,依据种子预定义由给定的shape布局中生成的关键字(key)建立hash索引,通过查找hash索引筛选候选位置以减少种子的候选位置个数,并运用Hough变换将种子命中进行分组操作,将其聚集为粗对准的形式,然后采用简洁de Bruijn图结构压缩存储和索引k-mer,以使得在确保正确比对百分比的同时,减少比对时间和所需的存储空间.
2 算 法
2.1 算法思想
细菌、哺乳动物等物种中存在大量重复的DNA子序列,尤其是在人类基因中超过50%的位置出现重复子序列.为能够使用尽可能少的存储空间,快速准确地将存在较多重复子序列的测序序列和参考基因组进行比对,本文给出一种改进的短序列精确比对算法.算法的关键是要快速地确定出参考基因组上可能对准序列的区域.区域选择依赖于在测序序列和参考基因组之间找到种子,并将其聚类为粗对准形式.算法的第一阶段,采用基于空位种子(gapped seeds)[19]搜索策略的区域选择方法来筛选比对的候选位置,以尽可能地减少候选位置[20],从而有效地减少搜索空间;然后,运用Hough变换将种子命中聚集为粗对准形式.第二阶段,生成参考基因组对应的简洁de Bruijn图,将测序序列与生成的de Bruijn图进行映射定位.第三阶段,验证粗对准中的候选位置子序列,以生成最终的序列对准结果.
2.2 算法描述
为便于算法描述,首先说明算法使用的参数的含义.其中全局参数bin_id表示所在区域下标,bin_value为所在区域命中个数,bin_value_size表示区域命中个数的规模,|r|为序列r的长度,|k_index|表示索引的规模,hit_counts表示hit计数,total_num_hits为总的种子命中数量,G表示参考基因组.局部参数x表示测序序列read坐标,y表示参考基因组坐标,l_local表示参考基因组与序列read的相对位置坐标.
为方便理解比对算法,下面介绍一些相关概念和知识.空位种子搜索策略由Burkhardt等人提出,其中q-gapped seeds表示非连续shape(模式)的长度为q的字符子串[19].例如,字符串ACAGCT中的3-gapped seeds的shape“1101”是ACG,CAC和AGT,其中“0”被定义为“do not care(DC)”字符的位置.文献[19]的研究表明,gapped seeds允许快速地对不精确匹配进行敏感查找,在种子的预定义“do not care(DC)”碱基位置中允许变化(包含插入和缺失).空位种子(gapped seeds)查找策略是基于Levenshtein距离的种子查找方法,在序列比对中它比核酸和氨基酸序列分析中的连续种子(连续q-grams,连续k-mers)更敏感[19].
通过构造参考基因组的hash索引来实现基于Levenshtein距离的空位种子查找策略,其中q-gapped 种子的子序列是由shape布局(layout)中生成的关键字进行hash索引的,该索引仅包含用于构造关键字的碱基,而不包含DC碱基(见图1中的“Do not care”碱基).

图1 用于索引构建和查找的插入空位的种子结构示例Fig.1 Example of gapped seeds structure for index creating and search
在索引的查找阶段,为每个shape构造多个关键字并用于检索.对于每个DC碱基,构造3个查找关键字:
1)DC碱基匹配或误配所有种子位置的关键字.见图1中的匹配或误配种子.
2)包含DC碱基的关键字.该关键字在指定位置最多允许一个删除(因为indel的长度一般为1bp).见图1中的删除种子.
3)不包含DC碱基及其后碱基的关键字.该关键字最多允许一个插入碱基和一次匹配或者不匹配碱基.见图1中的插入种子.
于是,每个shape建立d3个关键字,d表示shape中DC碱基的个数.基于Levenshtein距离的最佳shape的计算困难性[21,22]和对一系列组合的经验评估,本文选择以下的互补shape组合进行区域选择:1111110111111(6-1-6 shape)和11110111101111(4-1-4-1-4 shape),其中1表示包含的碱基,0表示DC的位置.本文为每个shape分别建立自己的hash索引.在参考基因组中每个种子出现的位置,搜索找到相关的两个互补shape,并将所有的命中执行下一步的分组操作,从而将候选位置上的种子聚类得到粗对准形式.
本文运用Hough变换方法获得分组种子命中对角线,以进一步完成区域选择(见图2),其中Hough变换用于检测诸如线、圆和椭圆的形状的处理,它定义从图像点到累积器(accumulator,基地址寄存器)的空间称为Hough空间的映射.对于线检测的情形,若笛卡尔空间中给定的一组点(一组种子)是共线的,则它们的关系可以用具有公共斜率m和截距c的线性方程表示:
y=mx+c
(1)
其中x和y是直角坐标系中的坐标(x,y)的元素.使用Hough变换确定描述给定点集(种子集)所在直线的参数m和c.本文可使用线性回归技术来确定给定点集的共线问题,则式(1)可转换为双参数空间:
c=-mx+y
(2)
给定直角坐标系中的点(x,y),其参数空间表达被定位为一条直线.若有多个坐标位置,则每个位置被转换为参数空间中不同的直线.它们的交叉点在方程(1)的坐标系中指定了候选线的位置.在Hough空间的映射定义的累积器空间中,参数m和c转化为坐标,从而获取各自取值的有限区间,通过查找每个(m,c)坐标并增加其计数,最后高于阈值的坐标都可被选为候选线.
根据确定分组种子命中对角线方法来获得种子粗对准的形式(见图2),结合参考基因组和测序序列组成的平面直角坐标系,单个种子的命中在此坐标系中用k-point(p,t)表示,其中p是种子在测序序列read上的位置,t是种子在参考基因组上的位置.当序列没有包含错误且是由序列模拟器生成时,k-points集合在直角坐标系中是完全共线的.m是已知的,只需要确定截距参数c,即可找到精确的映射位置.同时,c对应于参考基因组上(已经离散)的坐标,因此可确定分组种子对角线位置(见图2).对于每个k-point(p,t),它的c参数值可由(3)式确定:
c=t-p
(3)
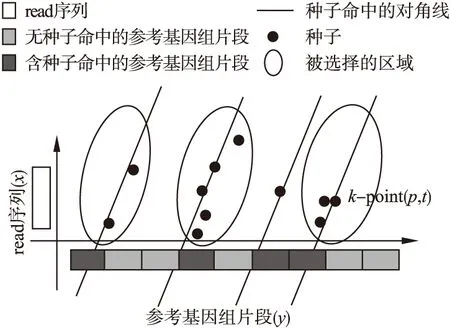
图2 对候选种子进行区域选择Fig.2 Region selection by clustering of candidate seeds on the reference
算法1描述了基于区域选择和简洁de Bruijn图的短序列精确比对算法(Short-read alignment using region filtering and compact de Bruijn graph,简记为SRA-RFCdBG)
算法1.SRA-RFCdBG
输入:参考基因组G,测序序列read集合R;
输出:包含R在G上的正确比对百分比的结果results;
Begin
1.解析参考基因组G建立k-mer文件;
2.依据k-mer文件生成overlap表格;
3.index←对参考基因组G建立k-mer索引;
4.fori=0 to |R|-1 do
5.regionsi←region_selection(Ri);//对Ri使用算法2进行
区域选择
6.end for
7.dBG←对regionsi生成简洁de Bruijn图;
8.results←测序序列read集合R与dBG的对准结果;
End
算法2.region_selection
输入:参考基因组G,read序列r,k-mer长度k,基于G建立的索引k_index,设定的区域大小bin_size,最小阈值min_percent;
输出:输出筛选后的种子区域向量bins;
Begin
1.bins←利用k_index和G创建初始区域向量;
2.total_num_hits←0;
3.fori=1 to |r|-14 + 1 do //选取14-mers作为种子
4. fork_index_id= 1 to |k_index| do
5.index←k_index[k_index_id];
6. ifindex≠NULL then
7. 根据(6-1-6)模式建立shape,获得SubSeed1和
SubSeed2
8. 将SubSeed1和SubSeed2根据DC分别构建三种key
对应误配,插入种子,删除种子,进行位置查找,获得
命中集Hitseti
9. 根据(4-1-4-1-4)模式建立shape,获得SubSeed3、SubSeed4和SubSeed5
10. 将SubSeed3、SubSeed4和SubSeed5根据DC分别构建三种key对应误配,插入种子,删除种子,进行位置查找,获得互补命中集reHitseti
11. 统计Hitseti和reHitseti中相同的候选位置作为候选区域,进行区域选择,并统计命中数,记作hit_counts
12.total_num_hits←total_num_hits+hit_counts;
13. forj=1 tohit_countsdo //Hough变换
14.x←i;//序列r的坐标x
15.y←seed_position(hit[j]);//G的坐标y
16.l_local←y-x;//绝对坐标转化为hit本地坐标
17.bin_pos←⎣l_local/bin_size」;
//bin_pos为种子区域bin所属的位置
18.bin_value[bin_pos]←bin_value[bin_pos]+1;
//第bin_pos个区域的命中数
19. end for
20. end if
21. end for
22.end for
23.max_value←max_element(bin_value)//bin_value最大值
24.fori=0 tobin_value_size-1 do
25. ifbin_value[i] >min_percent*max_valuethen //保
留大于阈值的区域bin
26.bin.bin_id←i;
27.bin.bin_value←bin_value[i];//区域bini命中数
28.bins.push(bin);//满足条件的区域bin增加到种子区域向量bins
29. end if
30.end for
31.依据bin_value将种子区域bins按降序排序;
End
2.3 算法分析
本文给出的序列比对方法同时考虑了“替换”和“indel(插删)”错误类型,其中“替换”类型错误会导致区域选择时满足条件的c值的最大计数减少,而“indel”类型错误会影响种子命中的对角线位置并使得正确位置c值的最大计数更准确.此外,对于算法2中种子区域bin的每个种子命中,它增加了使用式(3)确定的参数c值所对应的bin_value,然后按照命中数降序对筛选后的种子区域向量bins排序.为将搜索限制为最可能的区域,仅选择大于阈值的区域进行比对,以保持或提高正确比对百分比,且减少比对时间.
设read序列集R共有|R|=n条长度为l的序列.算法2在序列r中搜索索引index对应的参考基因组与种子的命中hit,所需时间为O((l-k+1)×|index|×|hit|),其中|index|表示index的大小,|hit|表示种子命中的规模.算法1中步4迭代n次;步5所需时间为O((l-k+1)×|index|×|hit|);步8中,序列r在比对中搜索遇到的简洁de Bruijn图的分支节点个数最多为b,每个节点有4个输出弧,最坏情形下要搜索4b个节点,搜索时间为|seeds|×O(4b+l-k-1+b),其中|seeds|为区域选择中的种子个数.算法1所需时间如下:O(n×(l-k+1)×|index|×|hit|)+O(n×|seeds|×(4b+l-k-1+b))=O(n((l-k+1)×|index|×|hit|+|seeds|×(4b+l-k-1+b))).
因此,算法SRA-RFCdBG的时间复杂度为O(n((l-k+1)×|index|×|hit|+|seeds|×(4b+l-k-1+b))),其中l>k,b≤l-k+1.而算法BrownieAligner[18]比对时间与正确比对百分比均与测序序列的长度l和分支节点数b′有关,其时间复杂度为O(n×|seeds′|×(4b′+l-k-1+b′),其中|seeds′|为种子个数,b′为比对搜索中遇到的分支节点个数.算法SRA-RFCdBG采用区域选择方法筛选候选位置来减少候选位置个数,使得种子数量和节点数有所减少,即|seeds|小于|seeds′|、b小于b′、4b远远小于4b′.因此,算法SRA-RFCdBG所需时间少于算法BrownieAligner.
本文采用简洁de Bruijn图[23]结构来完成比对.该图结构是一种压缩和索引标记树,类似于XBW-transform[24]结构,是压缩和索引字符串的BWT[25]的扩展.简洁de Bruijn图是de Bruijn图的一种紧凑表示,其需要m(2+logσ)个二进制位的存储空间,(2+logσ)的值不受k值的影响,且σ是字母表的大小(在蛋白质序列比对中,σ=4).而算法BrownieAligner的空间复杂度O(mk),其使用的de Bruijn图中的k取值为31.这表明本文算法SRA-RFCdBG所需的内存空间小于算法BrownieAligner.
3 实 验
3.1 实验环境与数据
实验使用的计算机为8核Intel(R)Core i7-6700k CPU@4.00GHz处理器,内存容量为32GB,操作系统为64位Ubuntu18.04LTS,采用C++语言编程实现算法.采用模拟数据集与真实数据集进行实验测试.对于3个参考基因组:大肠杆菌(E.coli str.K-12 substr.DH10B,E.coli)、人类第21条染色体(Humanchr-21,Hc21)和果蝇(Drosophila melanogaster,DM),使用ART[26]模拟器在两种不同的Illumina平台HiSeq 2000(100bp)和HiSeq 2500(150bp)上,生成长度分别为100bp和150bp的模拟数据序列(reads),见下一页的表1.真实数据采用Illumina平台上的数据集,参考基因组和测序序列从NCBI1网站获得,参考基因组规模从2Mbp到116Mbp,见下一页的表2.依据实验测试结果将所允许的种子区域向量bins最小阈值min_percent设为75%.
对于真实序列与参考基因组比对,首先使用BWA[27]将序列reads与参考基因组比对生成bwa.sam文件,其次使用samtools[28]从bwa.sam文件中提取出通过双端(paired-end)序列(将序列存储为正反两条序列形成的序列)比对方式正确映射到参考基因组,并存储到mappedPairs.sam文件中.接着使用基于CIGAR字符串和MD标记的sam2pairwise2重建每个序列的双端序列.最后使用Python脚本从双端序列和初始的真实数据中提取出无错误的参考基因组,以评估真实数据集序列与参考基因组比对的正确比对百分比.实验将本文算法SRA-RFCdBG与有其他代表性的同类代表性算法BGREAT[16]、deBGA[17]和BrownieAligner[18]进行性能比较.首先从参考基因组构建简洁de Bruijn图,然后将测序序列(reads)与生成的简洁de Bruijn图进行比对.我们使用GNU时间命令测量算法运行的(wall clock)时间.
3.2 模拟数据集上的实验
表3给出了在模拟数据集S1~S6上,4种算法将序列与参考基因组进行映射比对获得的正确对准百分比.
从表3可见,对于6种模拟数据集,与其他3种算法相比,本文算法SRA-RFCdBG均获得最高的正确对准百分比.这是由于SRA-RFCdBG算法采用的区域选择方法进行筛选候选位置时考虑了空格符号对比对的影响,这样可以减少序列与参考基因组比对的候选位置个数.此外,Illumina平台产生的序列存在的主要错误类型为“替换”,但也存在“插入和删除(indel)”错误.SRA-RFCdBG算法通过同时对这两种类型错误的处理,提高了种子命中率,从而获得更高的正确对准百分比.从表4也看到:每种算法在人类基因组数据集(S3,S4)上的正确对准百分比都低于其他4个数据集(S1,S2,S5,S6)上的正确对准百分比.这是由于人类基因组(S3,S4)中碱基序列重复率较高,导致算法将S3、S4数据集中序列与参考基因组比对时,获得正确对准的百分比较低.
图3给出了在6种模拟数据集S1~S6上,4种算法比对一百万条序列所用的运行时间.
从图3可以看出,在S1~S5数据集上,与其他3种算法相比,本文算法SRA-RFCdBG所需的时间最少.之所以获得这样的结果,是因为算法SRA-RFCdBG采用区域选择方法筛选搜索区域,减少了搜索空间,从而减少了比对的候选位置个数,减少比对计算量.对于S6数据集,算法SRA-RFCdBG所需的比对时间稍多于BGREAT所需的时间,但少于其他两个算法所需的时间.这是由于BGREAT采用早期停止机制,对数据集S6上的序列比对时,当序列碱基不匹配的数量快达到设置的阈值时,算法停止探索de Bruijn图的节点;而SRA-RFCdBG算法为了获得更高的正确对准百分比,采取在筛选后的区域中计算每个分支的对准计分上限,直到无法改进当前找到的最佳解决方案才丢弃分支,其所需的计算量稍高于BGREAT算法的计算量,但低于deBGA和BrownieAligner算法的计算量.也就是说,对于重复率率高达50%的大数据集S6的序列比对,本文算法SRA-RFCdBG通过增强一定的计算量来获得提升正确对准百分比.

图3 算法在模拟数据集上比对一百万条reads所用的时间Fig.3 Average runtime of tools to align 1M reads for the simulated datasets

表1 实验使用的模拟数据集Table 1 Artificial datasets used for the evaluation of graph aligner tools
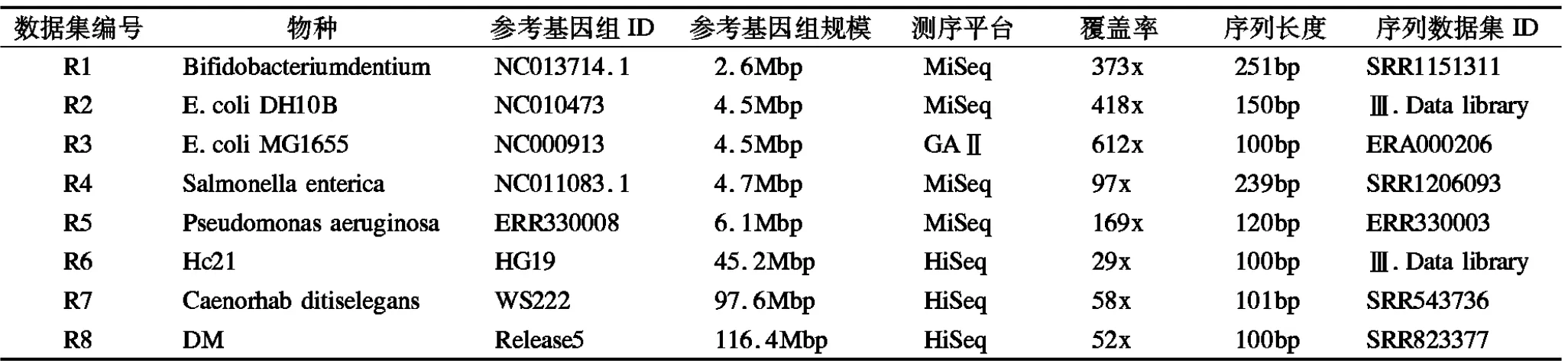
表2 实验使用的真实数据集Table 2 Real datasets used for the evaluation of graph aligner tools
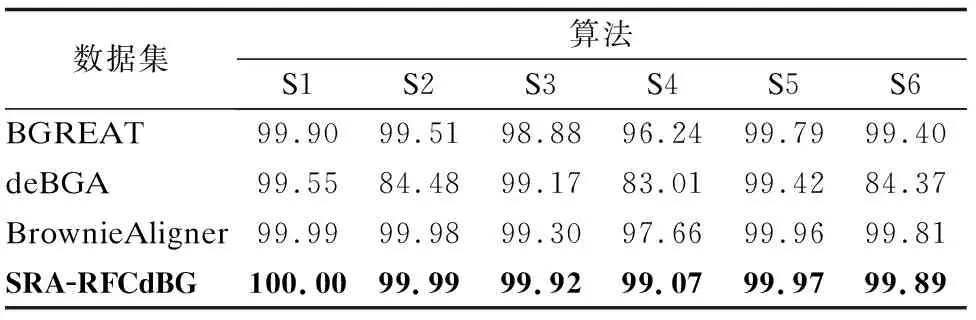
表3 模拟数据集上正确对准百分比Table 3 Percentage of correct aligned reads on simulateddatasets
3.3 真实数据集上的实验
为评测算法在真实数据集上进行序列比对的效果,表4给出4种算法在8个真实数据集R1~R8上正确对准测序序列与参考基因组的百分比.表4的结果表明,本文算法SRA-RFCdBG在细菌基因组(R1-R5)和真核基因组(R7,R8)上正确对准序列与参考基因组的百分比均高于其他3种算法.这是因为算法SRA-RFCdBG采用基于空位种子的区域选择方法对种子进行筛选,根据DC碱基构造的不同类型的查找关键字构建hash索引,索引查找两个满足条件的互补shape,从而完成近似匹配的敏感查找,这样即使在空位中存在“indel”的情形,也可以找到对应匹配的种子;而其他3种算法未考虑该情形对比对结果的影响,未能找出空位中存在“indel”错误的匹配的种子,这导致了较低的正确比对百分比.对于人类基因组的真实数据集R6,算法SRA-RFCdBG的正确对准百分比略微比deBGA的正确对准百分比低0.10%,但高于其他2种算法BrownieAligner和BGREAT的正确对准百分比.整体而言,相较于其他3种算法,算法SRA-RFCdBG在8个数据集上获得了更高的正确对准百分比.
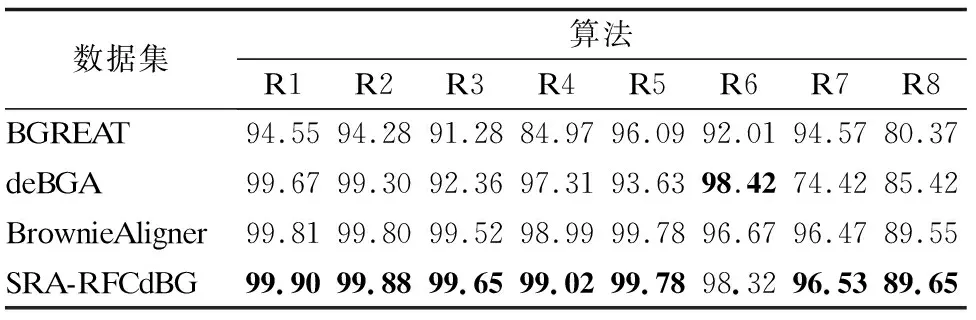
表4 真实数据集上正确对准的百分比Table 4 Percentage of correct aligned reads on real datasets
为评估算法在真实数据集上的运行效率,图4给出了4种算法在真实数据集上将一百万条序列reads与参考基因组进行比对所需的运行时间.
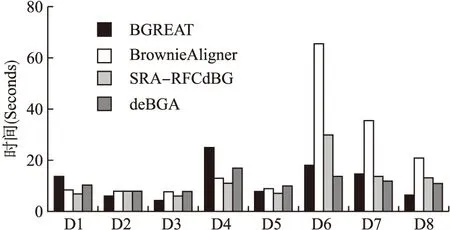
图4 在真实数据集上比对一百万条reads所需的时间Fig.4 Average run time of aligning 1,000,000 readsfor the real datasets
从图4中可以看出,对于R1、R4和R5这3个数据集,4种算法中,算法SRA-RFCdBG所用的时间最少.对于3个较大的数据集R6、R7和R8,算法SRA-RFCdBG的运行时间明显比BrownieAligner低.这是因为算法SRA-RFCdBG采用基于空位种子策略的区域选择方法进行筛选,对种子进行“预定义”,利用从shape布局中生成的关键字hash索引,快速地进行近似匹配的敏感查找,从而减少比对的候选位置的个数,尤其是对于重复率较高的基因组,可减少比对的候选位置的个数更多,有效减少了需搜索的空间,同时提高了正确比对的百分比.对于R6、R7和R8数据集,算法SRA-RFCdBG所需的时间比deBGA稍多一点.这是因为deBGA利用RdBG-index(Reference de Bruijn Graph-index)实现基于de Bruijn图的种子扩展方法,可以更快地处理参考基因组中的序列重复[17].对于数据集R2、R3和R8,算法SRA-RFCdBG所需的时间比BGREAT稍多一些,这是因为BGREAT算法的实现采用最小完美hash索引,它用来索引以(k-1)-mer开始或结束的序列片段的每个重叠部分,减少了查询时间.需要指出的是,虽然deBGA和BGREAT在某些数据集上完成比对所需的时间少一些,但它们获得的正确比对百分比低于本文的算法SRA-RFCdBG.
综合模拟数据集和真实数据集的序列比对实验结果表明,除了个别情形之外,本文算法SRA-RFCdBG获得的序列正确比对百分比均高于其他3种算法;在比对效率方面,SRA-RFCdBG优于算法BrownieAligner,与算法BGREAT和deBGA相比各有优势.
4 结束语
对于海量的测序序列reads与存在许多重复子序列的参考基因组的比对问题,本文采用基于空位种子搜索策略的区域选择方法来筛选候选位置,可以减少比对的候选位置,有效减少了搜索空间,在提高或保持正确比对百分比的同时减少了比对计算时间,尤其是对高重复率的序列进行比对,本文算法获得了更高的正确对准百分比;此外,通过采用简洁de Bruijn图仅存储由参考基因组生成的de Bruijn图中m条边的字符串和长度为σ的数组,减少了比对过程所需的内存容量,使得算法所需的存储空间下降到m(2+logσ)个二进制位,比对所需的内存容量不受k-mer长度k的影响.
近年来,随着更多的基因组可用,高通量测序技术的新应用需要将海量的测序序列与多个参考基因组对准[29].如何在既确保正确比对百分比,又能快速完成海量测序序列与多个参考基因组的比对工作,是一个值得继续研究的问题[17].下一步工作将本文算法研究扩展到海量测序序列与多个参考基因组同时比对的情形.

