三维场景的实时无人机航迹规划方法
陈 朋,汤粤生,俞天纬,江勇奇
1(浙江工业大学 计算机科学与技术学院,杭州 310023)2(浙江工业大学 信息工程学院,杭州 310023)
E-mail:ystang@zjut.edu.cn
1 引 言
近些年来,随着相关技术的不断发展,无人机越来越广泛地应用于物流、设施巡检、灾后救援和城市安防等各种场景.其中,多数应用场景要求无人机具备自主导航能力,并且在飞行过程中能够规避障碍以完成给定任务.航迹规划技术是实现无人机自主导航的关键技术之一,其可分为前端路径搜索和后端航迹优化[1],区别在于前者获得的路径通常存在不自然转向并且不包含无人机的动力可行约束,不适合直接用于无人机飞行,需要通过后者进一步优化,生成适用于无人机飞行的航迹.
在前端路径搜索方面已经有一些不错的工作.LaValle[2]提出了快速探索随机树(Rapidly-exploring Random Tree,RRT)算法,从配置空间中随机地抽取样本,并引导树向目标生长.RRT算法虽然能够高效地找到可行的路径,但不具有渐进最优性.此后,Karaman等人[3]对其进行改进并提出了RRT*(RRT算法的变体)、概率路图法(Probabilistic Roadmap*,PRM*)等一系列基于采样的渐进最优方法,在这些方法中,随着样本数的增加,最终趋近于全局最优解.郗枫飞等人[4]针对RRT系列算法面对复杂地图时随机采样效率低和路径重复性差的问题,提出一种基于模拟植物生长引导的RRT移动机器人路径规划算法,提升了路径寻优的稳定性和效率.另一方面,一些研究人员提出了基于节点的路径搜索方法,将配置空间离散化成一系列的节点,然后定义一个成本函数,搜索每个节点以找到成本最小的路径.该类方法可以与其他方法相结合,实现全局最优,适合实时应用场景,典型的方法有ARA*[5]、JPS[6]和Hybrid-state A*[7]等.
在后端航迹优化方面,前人也提出了多种不同的方法.王玉宝等人[8]根据机器人运动学特征,提出一种时间最优轨迹规划算法,采用简化粒子群模型和高项式插值模型对粒子群算法学习因子进行动态调节,在保证运动轨迹时间最优的同时,弥补了基本粒子群算法局部收敛的不足.郑红波等人[9]提出了一种基于层次包围盒碰撞检测的路径规划优化算法,在原始A*算法基础上,采用粗试探和精搜索的策略进行路径规划,可以规避无法通过的道路,提高了时间效率.Mellinger等人[10]最先提出了Minimum snap轨迹生成方法,由分段多项式函数表示轨迹,并将轨迹生成问题拟合成二次规划问题,但该方法直接对多项式系数进行求解,容易陷入数值不稳定问题.对此,Richter等人[11]利用了代入置换技术,将问题转化成无约束的二次规划,间接求解多项式系数,解决了文献[10]容易出现的数值问题.为了能适应障碍物密集的复杂环境,许多研究人员[12-14]提出了构建安全飞行走廊,该飞行走廊由若干凸区域构成,可将轨迹限制在该安全区域内,但该类方法会引入大量的不等式约束,导致二次规划问题的求解难度增加.此外,Zucker等人[15]把轨迹规划问题表示为最小化两个成本项:一个是对轨迹与障碍物碰撞的惩罚,另一个是轨迹本身的平滑性.但该方法是针对离散的轨迹点进行优化的,相对来说更适合用于机械臂的控制.在此基础上,Oleynikova等人[16]采用了连续时间分段多项式来表示轨迹,即整条轨迹由若干段以时间为自变量的多项式组成,无需对状态空间或时间进行离散操作,同时对于任意给定的时间能够快速评估高阶导数的连续性,有利于无人机的飞行控制,但该方法生成安全轨迹的成功率并不高,只有0.6左右的成功率,无法保证实际应用的安全性.受文献[16]的启发,本文对碰撞代价函数进行优化,并显式地引入了无人机的动力可行约束,在保证实时性的同时大幅度地提高了其在复杂环境中生成安全轨迹的成功率.本文的主要工作可归结如下:1)改进A*算法的启发函数,使其更适应无人机的三维运动特征,并利用梯度信息筛选关键航点,有利于后端航迹优化的进行;2)优化碰撞代价函数,并显式地引入无人机的动力可行约束,构建二次规划模型,使优化后的航迹更适合无人机飞行;3)与现有航迹规划方法对比,实验结果表明所提出的方法在保证实时性的同时具有更短的航迹长度和更高的成功率.
2 前端路径搜索方法
2.1 改进启发函数的A*算法
A*算法是一种启发式搜索算法,通过使用启发式信息引导搜索决策提高搜索效率,同时保证路径的优越性.A*算法的成本函数由实际成本和估计成本两部分组成,如式(1)所示.
f(n)=g(n)+h(n)
(1)
其中,n是当前的扩展节点,f(n)是从起始节点经过当前节点n到目标节点的最佳路径成本估计,g(n)是从起始节点到当前节点n的实际成本,h(n)是从当前节点n到目标节点的估计成本,通常也称为启发函数,它在成本函数中起着主导性的作用[17].如果h(n)总是小于或等于从当前节点n到目标节点的实际成本,那么A*算法就能确保找到最短路径,最好的情况当然是h(n)正好等于实际成本,此时在保证得到最优解的同时搜索效率最高.如果h(n)远小于实际成本,就会导致需要搜索的节点过多,搜索效率低下,而如果远大于实际成本,则可能得不到最短路径.因此,设计一个合适的启发函数就显得很关键.通常A*算法的启发函数多采用欧氏距离或曼哈顿距离,如式(2)和式(3)所示.
(2)
hm(n)=D·(dx+dy)
(3)
其中,he(n)和hm(n)分别表示采用欧氏距离和曼哈顿距离的启发函数,D′和D为节点间的移动代价,dx和dy分别为当前节点与目标节点的横坐标之间和纵坐标之间的差的绝对值.欧式距离可以表示任意方向的运动,但其不能体现栅格间的路径距离,并且由于平方根的存在,相对难以计算.而曼哈顿距离虽然计算简单,但是只能表示前后左右四个方向的运动,无法体现对角运动,通常得到的距离估计值会大于真实值.因此,为了能实现对角运动、距离估计值更贴近真实值,同时保证计算的相对简单高效,本文采用了对角距离.
hd(n)=D·(dx+dy)+(D2-2·D)·min(dx,dy)
(4)
其中,hd(n)表示采用对角距离的启发函数,D和D2分别表示两个相邻节点(有公共边)和面对角相邻节点(无公共边)之间的移动代价.如图1所示,为在二维栅格地图中采用曼哈顿距离和对角距离的方式进行路径搜索的区别示意图.
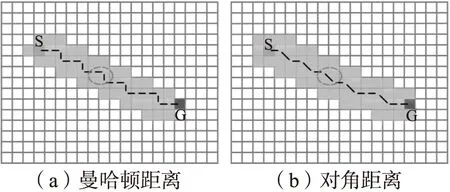
图1 采用两种距离进行路径搜索的区别Fig.1 Difference between two distances for path finding
其中,字母S、G分别表示起点和目标点,有阴影填充的栅格表示已搜索的节点,空白栅格表示未知节点,虚线段表示路径,椭圆状虚线圈出来的区域则表示两者区别所在,采用对角距离的方式需要进行min(dx,dy)次对角移动,但比采用曼哈顿距离的方式要节省2×min(dx,dy)次直线移动(即横向和纵向的移动).对于经常需要进行三维多自由度运动的无人机来说,显然二维的搜索算法是不能完全适应的.因此,沿着上面的思路将其推广到三维情况,即可表示面对角方向上的运动又可表示体对角方向上的运动,更加适应无人机的三维运动特征,本文提出适应三维多自由度运动的启发函数,如式(5)所示.
hd(n)=

(5)
其中,dmin=min(dx,dy,dz),D3为体对角相邻节点(无公共边)的移动代价.相对于采用曼哈顿距离和欧式距离的方式,我们改进的启发函数hd(n)不但能表示对角运动,使当前节点到目标节点的成本估计值更贴近实际成本,而且避免了直接计算平方根,保证了较高的计算效率,适合于类似无人机这样的机动性强、机载计算资源有限的平台上.
2.2 关键航点的筛选
前端用改进后的A*算法在栅格地图中找到的初始路径除了不包含无人机动力可行约束外,通常会存在一些不自然转向和许多冗余的航点,不适合直接用于无人机的飞行控制,而且大量的冗余航点也会加大后端航迹优化工作的难度.针对上述问题,本文利用航点间的梯度信息,滤除冗余航点,保留起点、拐点和目标点这些关键航点.如图2所示,有几何图形占据的区域表示障碍物,空白栅格则代表未探索(或无障碍)的区域,深色栅格表示路径上的航点,一系列的深色栅格构成了栅格路径,路径周围有浅色阴影填充的栅格表示已探索的节点,字母S、G分别代表起点和目标点,虚线段表示由关键航点构成的初始路径.而图2(c)中圆点等同于深色栅格也代表路径上的航点,箭头则表示相邻航点构成的向量.根据航点间的梯度信息,这里即是向量间的方向变化,就可以剔除掉冗余航点并筛选出关键航点,作为后端航迹优化的初始条件、约束条件等信息,在尽可能地保留初始路径信息的基础上,最大限度地减轻后端轨迹优化的难度.以上为了方便说明,先在二维情况下进行方法的描述,后将其推广到三维情况.如在图1和图2表示的二维栅格地图中,只采用式(4)作为启发函数并进行八邻域搜索即可,而对于三维栅格地图则是采用所提出的式(5)作为启发函数在当前节点周围相邻的26个节点进行搜索.对于关键航点的筛选,在二维和三维情况下都是通过判断向量间的方向变化来实现的.

图2 关键航点筛选示意图Fig.2 Diagram of key waypoints screening
3 后端航迹优化方法
有了前端路径搜索得到的初始路径和关键航点信息,本文在后端就可以对初始路径进行优化,解决初始路径存在的不自然转向、不够平滑和缺少动力可行约束等问题,生成适合于无人机自主导航的可行航迹.
3.1 问题描述
通常希望航迹能够满足一系列的约束条件,比如:起点或目标点的位置、速度和加速度,相邻航迹段连接处平滑,优化后的航迹无碰撞,满足无人机的动力可行约束(这里的动力可行约束是指无人机的最大速度、加速度、加加速度(Jerk)等限制)等等.而一般情况下满足约束条件的航迹可能存在无数条,实际问题中往往需要一条特定的航迹,因此需要构建一个最优函数,在可行航迹中找出特定的那条轨迹.
3.2 目标函数的构建
本文采用以时间t为变量的分段多项式来表示航迹,N阶M段的航迹如式(6)所示.
(6)
其中,μ表示x,y,z中的任意一个维度,pi,j表示第i段航迹的第j次项的系数,T1,T2,…,TM表示每段航迹终点的时间,而整条航迹的时间为T=TM-T0.
由文献[16]得到启发,本文显式地引入了无人机的动力可行约束,构建出如式(7)所示的目标函数.
ming=ω1·gs+ω2·gc+ω3·gd
(7)
其中,gs为平滑项保证航迹的平滑,gc为碰撞项使航迹与障碍物保持一定的安全距离,gd为动力可行约束项保证速度、加速度维持在可行的范围内.而ω1,ω2和ω3为对应项的权重,权衡三者在目标函数中所占的比重,任何一项系数设置过大都会导致该项占据主导地位、其他项作用微弱,设置过小则会导致该项所起的作用微弱,相应的结果也不尽相同.本文实验过程中将ω1,ω2和ω3分别设置为2.0,1.5和1.0,但系数设置并非绝对,应根据实际情况做出相应调整.
目标函数的平滑项可以表示成轨迹fu(t)的k阶导数的平方对时间t的积分,具体如式(8)所示.
(8)
进一步可以将其写成二次型形式pTQp,其中p为所有航迹段的多项式系数构成的向量,Q为海森矩阵.如文献[11]所提到的闭式求解法,本文引入一个映射矩阵A和置换矩阵C将多项式系数映射到多项式航迹段端点的导数,如式(9)所示.
(9)
这里矩阵A的作用是将多项式系数p映射为端点导数d,矩阵C则是将d中的固定导数dF(已知变量)和自由导数dP(未知变量)分离出来.因此,平滑项可以写成式(10)形式.
(10)
令CTA-TQA-1C为矩阵R,并根据固定导数和自由导数对其进行划分,可写成分块矩阵形式如式(11).
(11)
将式(11)展开,并关于自由导数dP进行求导,可得到平滑项相应的雅可比矩阵Js如式(12)、式(13).
(12)
(13)
其中,μ∈{x,y,z}代表x,y,z三个维度.令式(13)等于零,便可求得自由导数dP,再由式(9)就可间接得到多项式系数p.
对于目标函数碰撞项的构造,与文献[16]类似,本文也采用了可微函数c(f(t))沿航迹弧长的线性积分来表示,但不同的是本文采用了指数函数来表示可微函数c,如式(14)所示.
c(σ)=α·e-β(σ-σ0)
(14)
其中,σ为到障碍物的距离,这里可以通过建立一个欧式有向距离场来获取σ值,σ0为安全距离阈值,α为函数的幅值,β则代表变化率.从形式上来看,指数函数相比文献[16]中采用的分段函数具有形式简单,容易求导的特点.从实际物理意义上来看,如图3所示,本文希望当距离障碍物小于安全距离σ0时,c(σ)的值能迅速变得很大,使碰撞项成为整个目标函数的主导者,而当距离大于σ0时,c(σ)的值趋于平缓并且值相对较小,这样就能使航迹与障碍物保持着安全距离.因此,碰撞项gc可以写成式(15)的形式.
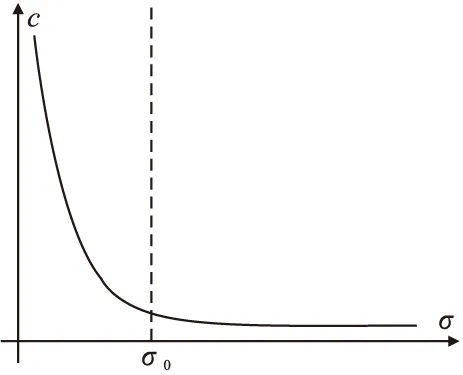
图3 碰撞代价函数示意图Fig.3 Diagram of collision cost function
(15)
其中,s表示弧长,f(·)和v(·)分别代表航迹上的点的位置和速度,Γk=T0+kδt.为了计算简单,这里将积分离散化变成求和的形式.因此,关于自由导数dPμ的雅可比矩阵Jc可写成如式(16)、式(17).
(16)
(17)
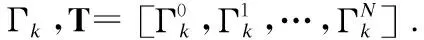

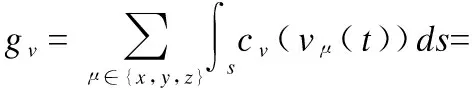
(18)
其中,aμ(t)为加速度函数.相应地,gv的雅可比矩阵Jv也可得到,与式(17)类似.此外,加速度约束项ga的构造与速度约束项gv的构造也类似,因为加速度函数aμ(t)是航迹多项式函数的二阶导数,所以这里不再赘述.因此,动力约束项gd=gv+ga,相应的雅可比矩阵则为Jd=Jv+Ja.
3.3 优化问题的求解
由3.2节的构造过程,可以得到整个目标函数g的雅可比矩阵J=ω1·Js+ω2·Jc+ω3·Jd,一般的非线性优化方法都可以用来最小化目标函数,比如梯度下降法、文献[16]里采用的拟牛顿法等.虽然目标函数是非凸的,可能存在多个局部最优解,但是由于目标函数具有在障碍物附近迅速趋于无穷大的特性,以及目标函数的每一项都可导、至少存在二阶导数,容易求得对应的海森矩阵,具有更好的收敛特性,因此即使得到的是局部最优解,也能保证其是安全可行的.本文这里采用了保守的凸可分近似算法(Conservative Convex Separable Approximation,CCSA)[18]来求解问题,其适用于具有大量变量的优化问题,即使目标函数的海森矩阵是密集型的,而且它能够保证从任何可行的起始点收敛到某个局部最小值.在求解过程中,固定变量dF为起点和目标点的导数,包括位置、速度和加速度,自由变量dP(即待求解变量)则为中间关键航点的相应导数.根据初始关键航点到最近障碍物的距离,设定自由变量dP的边界约束,保证其在适当的取值范围内.当满足设定的终止条件或者达到预设的最大优化时间限制时,整个优化过程结束,当前的解即为优化后的结果.实际求解结果表明,采用CCSA方法相比其他两种方法对本文优化问题能得到更好的局部最优解.
4 实验结果与分析
本文所提出的无人机航迹规划方法分为两个阶段:前端路径搜索获取初始路径、关键航点和后端航迹优化得到平滑、安全、满足无人机动力可行约束的航迹.下面章节先对实验平台进行简单的介绍,然后通过相关的实验数据分别对两个阶段进行定量和定性评估,并与现有航迹规划方法进行对比,验证所提方法的有效性.
4.1 实验平台介绍
三维场景中的无人机航迹规划仿真实验在Ubuntu系统下进行,基于ROS(Robot Operating System)框架采用C/C++语言进行算法软件设计,并利用ROS自带的可视化工具Rviz完成算法在三维环境下的可视化演示.所用实验平台的相关配置如下:处理器为Intel(R) Core(TM) i5-6500 3.20GHz× 4,内存大小15.6GB,系统版本为Ubuntu 16.04 LTS,ROS版本为Kinetic 1.12.14.
4.2 前端路径搜索方法
这里分别采用曼哈顿距离、欧式距离以及对角距离三种方式来表示A*算法的启发函数,在三维复杂仿真空间场景(20m×20m×8m大小,随机分布稠密障碍物,如图4所示)中,随机生成起始点和目标点(实际应用中诸如Intel Realsense深度相机、ZED双目相机等有效测量范围在0.1~20m之间,因此,实验设置取中值10m作为起始点和目标点的直线距离,随机生成的起始点和目标点满足该条件),然后分别进行3组实验,每组实验进行10次,最终结果为10次实验数据取平均值,评估结果如表1所示.图4为三维路径搜索实验示意图,图4(a)为关键航点筛选前的路径搜索结果,图4(b)为利用梯度信息筛选出关键航点.其中,由一系列浅色栅格组成的柱状体为障碍物,空白区域为自由空间(无障碍物),深色栅格代表搜索到的路径上的航点,字母S、G分别代表起始点和目标点.

图4 三维路径搜索示意图Fig.4 Diagram of 3D path finding
由表1可知,与采用曼哈顿距离表示启发函数的方法对比,本文改进的采用对角距离表示启发函数的方法在平均标准化长度(实际路径长度除以起始点到终点间的欧式距离)、航点总数以及关键航点数三方面都有所减少,虽然在平均时间上不占有优势,但是可以克服采用曼哈顿距离表示启发函数的方式无法实现对角方向上运动的缺点;与采用欧式距离作为启发函数的方法相比,本文改进的采用对角距离表示启发函数的方法在平均标准化长度和航点总数上与其相当,但在平均时间和关键航点数上占有比较大的优势.因此,相比于其他两种方法,本文优化的三维路径搜索方法在保证具有较快速度的基础上,能够保证找到最短的初始路径、最少的关键航点数,同时又能表示对角方向上的运动.
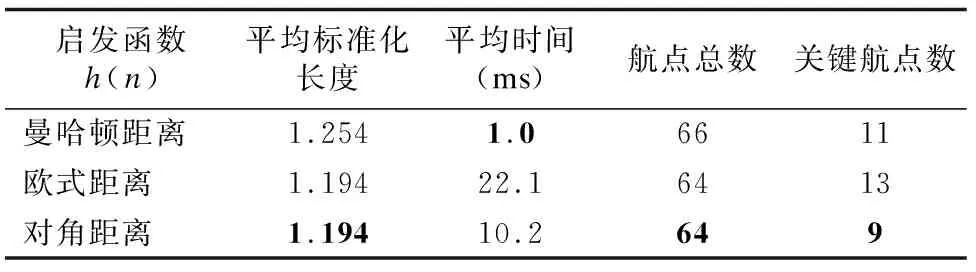
表1 采用不同启发函数的路径搜索对比Table 1 Comparison of path finding via different heuristic functions
4.3 后端航迹优化方法
本文分别与文献[11]和文献[16]所提出的方法进行对比,值得注意的是,这里只针对后端航迹优化方法进行评估,不包括前端的路径搜索.同前面一样也是在20m×20m×8m大小的三维仿真环境中,随机生成起始点和目标点,根据前端路径搜索环节得到的关键航点,并设置不同的障碍物密度,然后分别进行50次的航迹优化对比实验,最终结果为50次实验数据的平均值.表2表示在障碍物密度为0.2个/m2情况下的定量评估结果.其中,与文献[11]相比,本文方法在成功率、平均标准化长度和平均时间三个方面都有不错的表现;与文献[16]相比,本文方法在平均时间上略微高于文献[16]的方法,原因在于本文引入了无人机动力可行约束项,由此带来计算量的略微增加.而在成功率和平均标准化长度两方面,本文方法都具有一定的优势,特别是在场景障碍物密度不是很高的情况下,本文方法可以达到100%的成功率.

表2 不同航迹优化方法对比Table 2 Comparison of different trajectory optimization algorithms
图5展现了三种航迹优化方法的定性评估结果,其中曲线1代表文献[11]的方法优化的航迹,曲线2为本文方法优化后的航迹,曲线3则代表文献[16]的方法优化的航迹,字母S、G分别代表起始点和目标点,空白区域表示自由空间(无障碍),若干数量的柱状体则代表着障碍物.由图5可以观察到,曲线2始终保持着与周围障碍物适中的安全距离,不像另外两条曲线在某些地方会出现离障碍物很近的情况,容易出现碰撞危险.
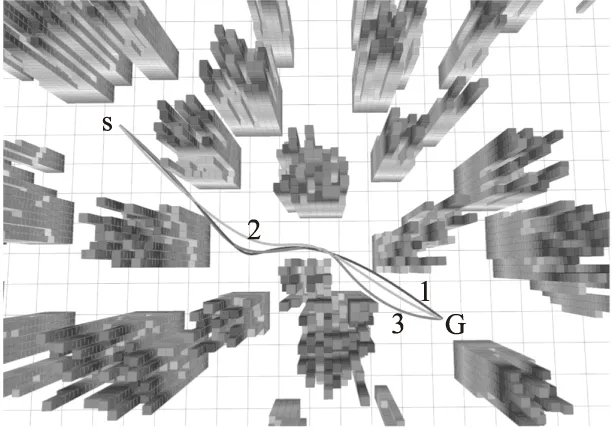
图5 不同轨迹优化方法对比图Fig.5 Diagram of different trajectory optimization algorithms
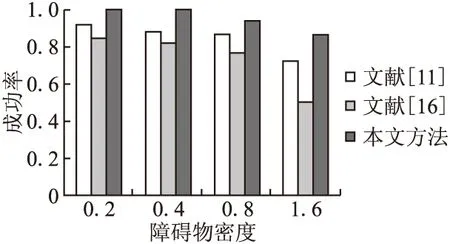
图6 不同障碍物密度下的成功率Fig.6 Success rate at different obstacle density
这也就是本文方法能够获得较高成功率的原因所在,对碰撞项的优化以及无人机动力可行约束项的引进所致.图6表示了三种航迹优化方法在不同障碍物密度下的成功率变化情况.随着障碍物密度的增加,三种航迹优化方法的成功率都逐渐下降,但相比其他两种方法,本文航迹优化方法下降的幅度最低并且维持着最高的成功率.此外,在图7中我们还给出了本文方法在不同障碍物密度下的航迹优化表现情况.其中,

图7 不同障碍物密度下的航迹规划图Fig.7 Diagram of trajectory planning at different obstacle density
字母S、G代表起点和目标点,两点间的曲线代表优化后的航迹,在曲线上或附近的单个栅格点则代表前端路径搜索得到的关键航点.实验过程中,算上前端路径搜索和后端航迹优化所需的时间总和基本都维持在50ms内,能够满足无人机实时航迹规划要求.
5 总 结
针对三维场景中无人机航迹规划的实时性和安全性问题,本文提出了一种基于关键航点的实时无人机航迹规划方法.该方法分为两阶段:首先,改进A*算法的启发函数,使其更适应无人机的三维运动特征,在此基础上利用航点间的梯度信息对初始路径进行关键航点的筛选,有利于后端航迹优化的进行;接着,显式引入无人机动力可行约束,并改进碰撞惩罚项,构建二次规划模型,对初始路径进行优化进而得到一条平滑、安全并且适合无人机飞行的航迹.实验验证表明,本文方法保持了较好的实时性,运行时间可达50ms内,同时一定程度上提高了航迹规划的成功率以及航迹的质量,在障碍物密度小于0.5个/m2的情况下,能维持在100%的成功率,并且优化后的航迹长度更短,更符合实际工程应用的要求.

