一种全局搜索策略的鲸鱼优化算法
刘 磊,白克强,但志宏,张 松,刘知贵,3
1(西南科技大学 信息工程学院,四川 绵阳 621000)2(中国航发四川燃气涡轮研究院,四川 绵阳 621703)3(西南科技大学 计算机科学与技术学院,四川 绵阳 621000)
E-mail:liuzhigui@swust.edu.cn
1 引 言
鲸鱼优化算法(whale optimization algorithm,WOA)是2016年由Seyedali Mirjalili 教授[1]提出的一种群智能优化算法,通过模仿鲸鱼在海洋中捕捉食物的搜寻过程,来寻找最优解.该算法具有结构简单、自身参数少的特点,在多元函数求解方面比传统粒子群优化算法[2]和遗传算法[3]的速度更快、精度更高.在实际工程中的应用也开始增多,Khaled等[4]使用WOA对电力系统的调度进行优化,实现了对无功功率的最优调度.Yu等[5]将WOA应用在控制器的参数整定中,优化后的参数可以使控制系统具有更强的鲁棒性.但是WOA也存在传统群体优化算法的弊端,全局搜索能力不足,算法寻优精度低等问题.
为了解决传统鲸鱼优化算法的缺陷,Oliva等[6]提出一种混沌鲸鱼优化算法,使用混沌策略指导鲸鱼位置更新,一定程度避免了陷入局部最优解.牛培峰等[7]将反向学习策略运用到鲸鱼位置初始化中,提升了算法的搜寻效率.目前已有大量改进的WOA算法提出,但大多的改进都没考虑到螺旋更新方式对算法寻优的影响,以及算法在全局搜索能力上的不足.
针对上述问题,本文提出一种全局搜寻策略的鲸鱼优化算法(global search whale optimization algorithm,GS-WOA).该算法采用变螺旋更新方式,增加鲸鱼寻优过程中的螺旋路径选择;使用自适应权重改变鲸鱼位置更新时的速度,动态调整权值来提升算法后期的收敛速度;通过最优邻域扰动的策略,来避免算法的早熟现象.为检验GS-WOA的寻优性能,在多个测试函数上进行仿真实验,结果表明了该算法具有更高的寻优精度和更快的收敛速度.
2 鲸鱼优化算法
鲸鱼自身体积比较庞大,在海里移动相对来说不是特别灵活,想要捕获更多的小鱼就需要一种独特的群体合作的方式,找到最多小鱼群的位置.鲸鱼的群体捕捉过程如图1所示,鲸鱼通过向上螺旋靠近目标,并逐渐缩小包围圈,最终到达目标鱼群的位置.根据捕食特点,WOA包括三种位置更新方式:包围猎物、旋转搜寻以及随机搜寻.
图1 捕猎示意图Fig.1 Hunting diagram
2.1 包围猎物
鲸鱼将目前搜寻到的猎物信息共享,然后鲸鱼向当前群体中最接近猎物的那头鲸鱼靠近,逐渐收缩整个鲸鱼群的包围圈,实现对猎物的包围.该环节鲸鱼位置更新公式为:
(1)
式中:t为迭代搜寻次数;X为鲸鱼位置;X*是全局最优位置;A和C为系数矩阵,表达式为:
(2)
式中:r1和r2是[0,1]均匀分布随机数;t为迭代次数;tmax为最大迭代次数;a为收敛因子,从2到0线性递减.
2.2 旋转搜寻
鲸鱼搜寻猎物是螺旋向上,慢慢靠近目标的方式,螺旋搜寻的表达式为:
(3)
式中:b为常数,可以改变螺旋的形状;l为[-1,1]均匀分布随机数.
鲸鱼在螺旋搜寻猎物的时候,还会收缩包围圈,所以为了模拟这种行为,需要包围猎物和螺旋搜寻同步进行.更新公式为:
(4)
式中:p为[0,1]之间均分布随机数.
2.3 随机搜寻
为了提升鲸鱼的全局搜索能力,让鲸鱼在搜寻猎物时具有一定的随机性,增加鲸鱼群的搜寻范围.
当系数|A|≥1时,说明该鲸鱼在收缩包围圈外,选择随机搜寻方式;当系数|A|<1时,说明该鲸鱼在收缩包围圈内,选择螺旋包围搜寻方式.随机搜寻更新公式为:
X(t+1)=Xrand(t)-A·|C·Xrand(t)-X(t)|
(5)
式中:Xrand为一个随机的鲸鱼位置.
以上三种搜索方式的结合构成鲸鱼优化算法.
3 改进的鲸鱼优化算法
通过分析发现,鲸鱼优化算法在收敛速度和全局搜索能力上还存在一定缺陷.根据标准鲸鱼位置更新方式,引入三种改进方式构成全局搜索策略提升算法的寻优能力.
3.1 自适应权重
受粒子群优化算法的启发,在鲸鱼的位置更新中加入一个随迭代次数变化的惯性权重w.在算法搜索的前期,削弱最优鲸鱼位置对当前个体位置调整的影响,提升算法在前期的全局搜索能力.随着迭代次数的增加,逐渐提升最优鲸鱼位置的影响力,使得其他鲸鱼能够快速收敛到最优鲸鱼的位置,提升整个算法的收敛速度.根据鲸鱼优化算法中更新次数的变化,选用迭代次数t构成的自适应惯性权值如下:
(6)
这样的惯性权值w具有一种在[0,1]之间非线性变化的属性,由于cos函数在[0,π/2]之间的变化特性,使得权值在算法初期较小,但变化速度稍快;在算法后期其值较大,但变化速度会减缓,这样可以充分保证算法收敛性.改进后的鲸鱼优化算法位置更新公式为:
(7)
X(t+1)=w(t)Xrand(t)-A·|C·Xrand(t)-X(t)|
(8)
在引入自适应权重之后的位置更新,会根据迭代次数的增加,动态调节权重大小,使得最优鲸鱼位置X*(t)在不同时刻对鲸鱼个体的指导不同.随迭代次数的增加,鲸鱼群的会集中向最优位置方向靠近,并且此时权值较大会使鲸鱼位置移动速度加快,进而加快算法收敛速度.
3.2 变螺旋位置更新
鲸鱼在搜寻猎物的时候,会根据目标位置与自身位置之
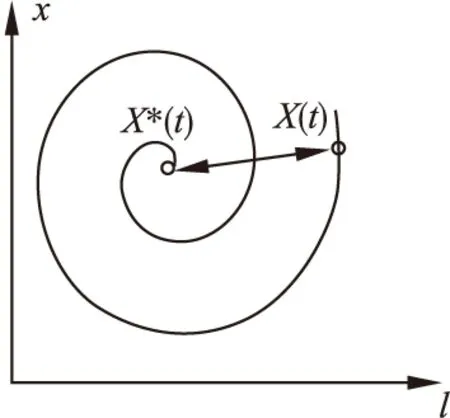
图2 螺旋更新位置Fig.2 Spiral update position
间的螺旋形状,调整每次位置更新的移动距离,如图2所示.在螺旋搜寻模型式(3)中,b是控制螺旋形状的常数,该参数一般设置为常数,每次位置更新按照不同的螺旋弧度进行速度调节.但是b设置为常值会导致鲸鱼在搜寻猎物时的螺旋移动方式过于单一,每次都是按照固定的螺旋线靠近目标,极易陷入局部最优解的误区,削弱算法全局搜寻能力.
针对该问题,为了使鲸鱼能够开发更多样的搜索路径进行位置更新,引入变螺旋搜寻的思想,将参数b设计为随迭代次数改变的变量,动态调整鲸鱼搜寻时的螺旋形状,增加鲸鱼对未知区域的探索能力,进而提升算法全局搜索能力.结合自适应权值后,新的螺旋位置更新公式如下:
(9)
参数b是根据螺旋线的数学模型进行设计的,在原有螺旋线模型的基础上,通过引入迭代次数,动态调整螺旋形状.这样设计的参数b会随迭代次数增加,使螺旋形状从大到小的变化.在算法前期鲸鱼以较大的螺旋形状搜寻目标,鲸鱼尽可能多的去探索全局最优解,提升算法的全局最优搜寻能力;在算法后期鲸鱼以小螺旋形状搜寻目标,提升算法的寻优精度.
3.3 最优邻域扰动
鲸鱼在更新位置的时候,一般都是以当前最优位置作为本次迭代的目标.在整个迭代环节中,最优位置只有在出现优于它的位置时才会更新,所以总的更新次数不多,导致算法搜寻效率不高.针对此,引入最优邻域扰动策略,将最优位置的附近随机搜索一遍,找到一个更佳的全局值,这样不仅可以提升算法的收敛速度,而且还能避免算法出现早熟.
最优位置产生随机扰动,增加其对附近空间的搜索,邻域扰动公式为:
(10)
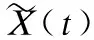
对于生成的邻域位置,采用贪婪的策略判断是否保留,公式如下:
(11)
式中:f(x)为x的位置适应值.如果生成的位置比原位置好,则将其与原位置替换,使其成为全局最优.反之,最优位置保持不变.
3.4 算法流程
改进鲸鱼优化算法的流程如表1所示.
3.5 算法复杂度分析
时间复杂度可以作为评判一个算法运算量的重要手段.在鲸鱼优化算法中,设算法中鲸鱼的规模为N,最大迭代次数为T,问题维度为D.可以得到WOA的时间复杂度为O(N*T*D).而GS-WOA在原有算法的基础上引入三种改进策略,从该算法流程可以看出,在加入自适应权重和变螺旋更新策略未增加循环次数,算法时间复杂度为O(N*T*D),而加入最优邻域扰动给算法外围增加了一次遍历种群的循环,增加了O(N*T)的运算量.对于整个算法的时间复杂度来说,增加O(N*T)的运算量不会对算法造成太大计算负担,总体来说GS-WOA的时间复杂度与标准WOA时间复杂度持平.

表1 算法流程Table 1 Algorithm flow
空间复杂度用来评判一个算法对内存空间的需求情况.在这里空间复杂度主要由鲸鱼的规模和所需求解问题的维数决定,GS-WOA和WOA具有相同的空间复杂度O(N*D).
4 算法性能测试
4.1 测试函数及性能指标
为了测试GS-WOA算法的寻优能力,在文献[1]中选择了11个基准函数.其函数特性如表2所示.算法寻优精度为实际寻得最优解与理论最优解之间的误差绝对值,本文采用两个评价指标:寻优精度的平均值(Ave)和标准差(Std).其计算公式如下:
(12)
式中:Xopt为理论最优解;N为总的实验次数.
4.2 优化算法的性能分析
使用GS-WOA算法在11个基准函数上进行测试.维数Dim分为30和200,并将其与GWO[8]、WOA和SM-WOA[9]算法进行比较,对比4种算法的性能指标.4种算法的参数设置相同:规模N为30;最大迭代次数为500.4种算法均单独测试30次,得到优化结果的平均精度及其标准差如表3所示,其中黑色粗体为较优结果.

表2 基准测试函数Table 2 Benchmark function

表3 寻优指标对比Table 3 Comparison of optimization indexes
从表3中可知,GWO算法的寻优精度普遍较低,只有在测试函数f3、f4上优于WOA算法.SM-WOA算法在寻优精度上面有所提升,但缺乏全局搜索能力,在函数f5、f6和f11上,算法的寻得的最优解和理论值有一定偏差.GS-WOA算法在这些测试函数上的寻优精度都优于其余对比算法,并且标准差相对较低,表明算法较为稳定,其中对函数f1、f3、f8、f10的求解,可以搜寻到理论最优值.当问题维数上升后,所有优化算法的寻优精度都有所降低,但GS-WOA算法仍然保持了较高的寻优精度和稳定性.
图3为WOA、MS-WOA、GWO和GS-WOA算法在基准测试函数上求解的收敛曲线对比图.
从图3中可以看出,GS-WOA算法的收敛速度普遍要比其余3种算法快,并且寻优精度更高.由图中(e)、(f)、(g)和(k)可以知,在函数f5、f6、f7和f11上,GWO、WOA和MS-WOA都陷入的局部最优解,而GS-WOA由于变螺旋更新方式提升了算法全局搜索能力,使得算法可以突破局部最优的限制寻找到新的全局最优解.总体来说,GS-WOA算法具有更高的寻优精度和求解能力.
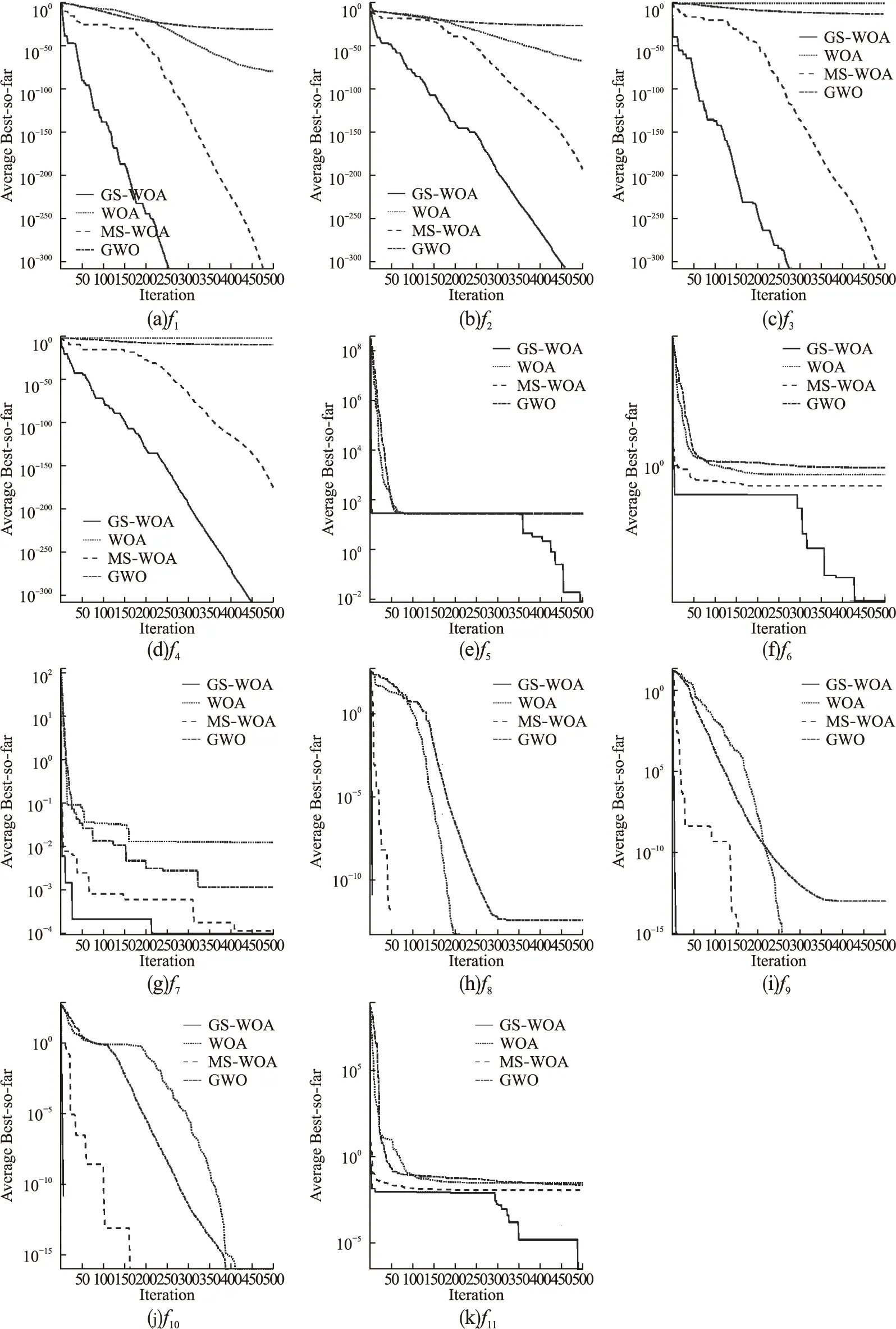
图3 收敛曲线对比图Fig.3 Convergence curve comparison diagram
为了验证GS-WOA改进策略的有效性,将其与CWOA[10]、W-SA-WOA[11]和IWOA[12]进行对比,基准测试函数任选择之前的11个,鲸鱼规模为30,最大迭代为500次,独立运行30次实验,并引用文献[10-12]中的一些数据,对比分析各算法性能指标,结果如表4所示(“-”表示参考算法未做该项实验),较优结果已用粗体标出.
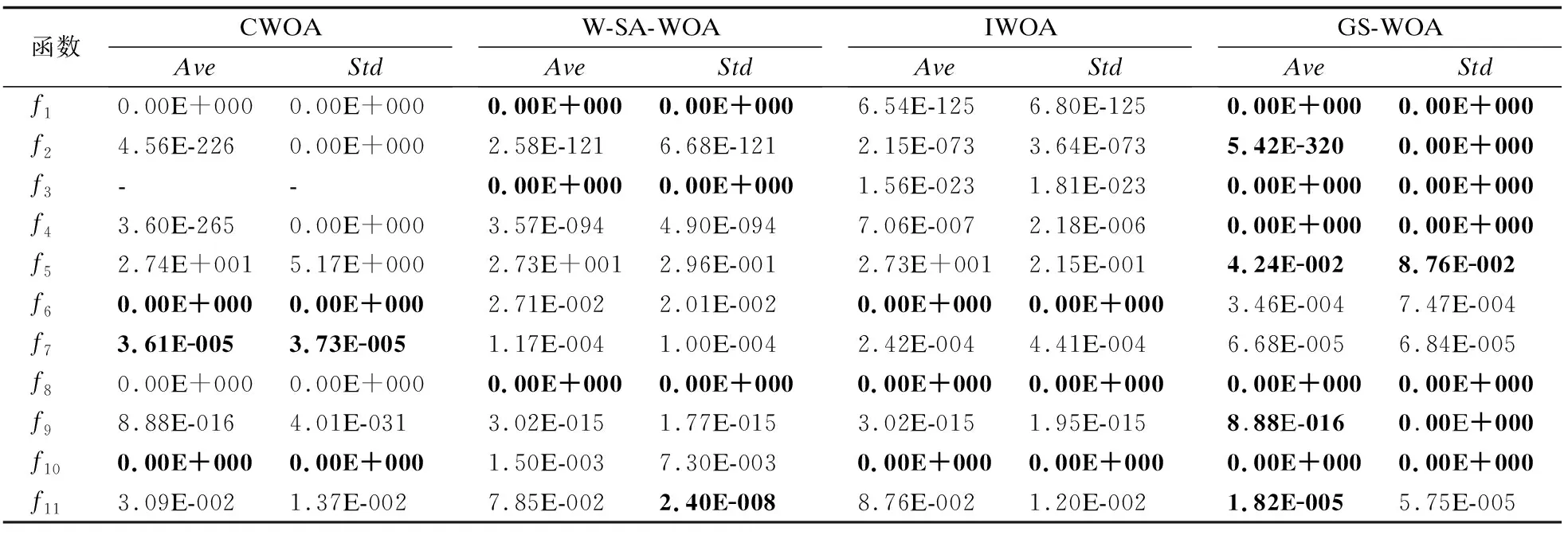
表4 与其他改进算法的对比Table 4 Comparison with other improved algorithms
由表4可知,在已给出的测试函数上,GS-WOA的寻优精度优于CWOA、W-SA-WOA和IWOA三种算法,并且具有较高的稳定性.
综上所述,GS-WOA在求解复杂函数的最优解时,比传统WOA的求解精度高很多,与目前改进的WOA算法相比,GS-WOA能找到更好的全局最优解.
5 总 结
鲸鱼优化算法是一种具有仿生寻优的智能优化算法,但是在处理复杂函数优化问题时仍存在一些局限性.本文分析了标准WOA的寻优过程,根据目前位置更新存在的问题,提出了相应的解决方法.为了防止WOA算法易陷入局部最优解,加入自适应权值、变螺旋更新和最优邻域扰动策略,调整鲸鱼位置更新的方式,动态调节鲸鱼向目标物靠近的速度,进而提升整个算法的全局搜索能力.通过在基准函数上的测试,结果表明了GS-WOA算法能够突破局部最优解的限制,获得更高的求解精度.相比于其他改进算法,GS-WOA具备更强的全局搜寻能力,证明了本文针对WOA提出的三种改进策略的有效性.

