改进VMD算法在管道泄漏检测中的应用

杨丹迪, 路敬祎, 周怡娜, 王 闯, 董宏丽

(东北石油大学 a. 复杂系统与先进控制研究院; b. 黑龙江省网络化与智能控制重点实验室, 黑龙江 大庆 163318)

0 引 言

管道运输因其成本低, 动力消耗小等优势, 被广泛应用于石油天然气的输送。目前, 由于管道运行年限的不断增加, 老化程度逐渐严重, 而且人为破坏、 盗取行为也严重威胁着油气管道的安全, 泄漏风险逐渐增大。 而管道泄漏将给社会造成很大的经济损失以及危害, 因此人们对管道安全问题非常关注, 对管道泄漏检测技术[1-4]的研究已成为国内外学术界的研究热点。目前管道泄漏检测方法有很多, 主要有负压波检测法、 声波法、 漏磁检测法、 光纤检测法和人工智能算法等。声波法[5-6]因其方法简单、 维护费用低得到了广泛应用。经验模态分解(EMD: Empirical Mode Decomposition)[7-8]是一种将时域信号按频率尺度自适应分解的数值算法, 非常适用于非平稳信号的分析, 但在信号分解时, 容易存在模态混叠现象, 从而导致分解的IMF分量失真。

Dragomiretskiy等[9]于2014年提出VMD(Variational Mode Decomposition)算法, 可以很好地抑制EMD方法的缺陷[10-11]。文献[12]将VMD算法与相关系数与峭度结合作为前置滤波处理, 选取合适滤波器长度及解卷积周期对重构信号进行最大相关峭度解卷积运算以实现对轴承故障进行准确分离, 并通过与EEMD(Ensemble Empirical Mode Decomposition)降噪后解卷积处理的对比, 验证了VMD前置滤波处理的优越性。文献[13]提出了一种VMD算法与模糊相关分类结合的自适应去噪方法, 能检测管道中出现的小泄漏, 与支持向量机方法相比具有更高的检测率, 但VMD算法存在预设尺度K难以选取及难以确定分解后有效的IMF分量的问题。文献[14]提出了互信息与VMD结合的去躁方法在天然气管道泄漏检测中的应用, 通过计算VMD分解后的IMF分量与原始管道信号的互信息值, 筛选有效的IMF分量进行重构, 克服了VMD在分解时选取IMF分量的盲目性。文献[15]提出VMD与豪斯多夫距离结合的方法对信号进行去噪, 先用VMD对信号进行分解后得到IMF分量, 计算各分量和信号的概率密度函数, 最后通过各分量的概率密度函数和原始信号的概率密度函数之间的豪斯多夫距离判断出有效IMF分量对信号进行重构。

基于以上研究, 为更好地选取VMD算法分解后有效IMF分量及解决信号中的噪声干扰问题, 减少高频段有用信息的丢失, 笔者提出了一种基于相关系数、 峭度和小波变换的VMD改进算法, 通过仿真及试验将笔者算法与其他算法进行对比, 以信噪比和均方误差作为性能指标, 验证了笔者提出的算法在信号去噪上的优越性和应用在管道泄漏检测中的有效性。

1 VMD算法及相关理论

1.1 VMD算法原理

VMD算法是一种可变尺度的信号处理方法, 可将一个实际信号f分解成K个模态函数, 使每个模态的估计带宽之和最小, 具体分解步骤如下。

1) 采用Hilbert变换, 计算每个uk的解析函数以获得其相应的单侧频谱

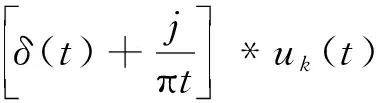
(1)

2) 对每个模态uk, 通过与其对应的中心频率的指数项混叠, 将每个模态uk的频谱转移到相应基带

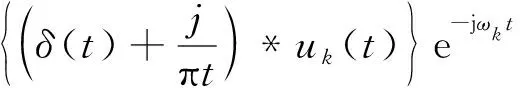
(2)

3) 由解调信号的高斯平滑度和梯度平方范数估计带宽。

4) 由上述步骤得到的约束变分问题为

(3)

其中uk={u1,u2,…,uk}为各模态函数,ωk={ω1,ω2,…,ωk}为各中心频率。

通过引入拉格朗日乘子λ(t)和二次惩罚因子∂将约束变分问题转换为非约束变分问题, 二次惩罚因子是典型的实现重构信号保真度的方法, 拉格朗日乘子则用于实现精确重构。将两者结合得到拓展的拉格朗日表达式如下

采用乘法算子交替方向法解决上述变分问题, 迭代优化uk+1、ωk+1、λk+1即可求得扩展拉格朗日表达式的“鞍点”, 变分问题的解为

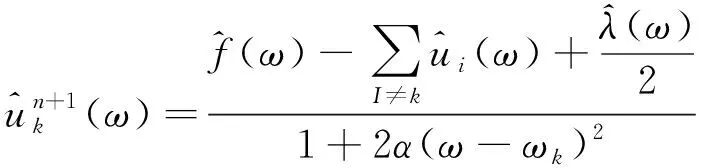
(5)

中心频率的更新方法为

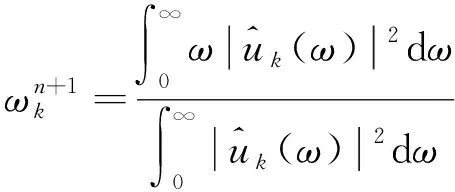
(6)

VMD算法迭代步骤如下。

1)初始化u1、ω1、λ1、n=0。

2) 令n=n+1, 执行整个循环, 更新uk。

3) 对所有ω≥0, 使

(7)

4) 重复步骤2), 步骤3)直到满足约束条件

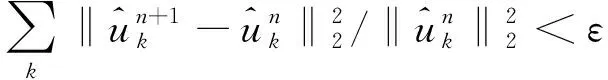
(8)

从整体上看, 在迭代求解变分模型的过程中各个IMF分量的中心频率和带宽不断更新, 直到满足迭代终止条件。最终, 根据信号的频域特征得到K个IMF分量, 完成了信号的自适应分割, 能有效避免模态混叠现象。

然而, VMD算法在迭代过程中需要预先确定IMF分量的个数, 但K值通常难以确定, 导致不能得到有效的IMF分量。

1.2 相关系数

相关系数(CC: Correlation Coefficient)是由著名统计学家卡尔-皮尔逊提出的, 用以反映变量之间相关关系密切程度的统计指标[16], 笔者引用相关系数判断IMF分量和原始信号之间的相关程度, 以两变量与各自平均值的离差为基础, 通过两个离差相乘反映两变量之间的相关程度。

相关系数的计算公式为

(9)

其中x,y为两个矢量,Ex,Ey为对应矢量的期望。r反应了变量之间相关程度的高低。

1.3 峭 度

峭度(Kurtosis)是描述信号波峰尖度的无量纲参数[18], 定义为信号的归一化4阶中心矩, 反映随机变量分布特性的数值统计量, 计算表达式为

K=E(x-μ)4/σ4

(10)

其中σ和μ分别为信号x的标准差和均值；E为信号x的期望值。

峭度指标对冲击信号较为敏感, 能较好地反映管道泄漏信号中的冲击成分, 信号中的冲击成分所占比重越大则峭度指标的绝对值也越大。而VMD算法分解出的高频模态分量包含噪声较多, 其冲击成分占比大、 峭度值高, 从而通过对信号的峭度分析可以实现VMD算法分解后有效模态分量的选取。

通过观察多组管道工况信号可知, 当VMD算法分解后的模态分量中无噪声或噪声成分比较少时, IMF分量的峭度值一般小于4, 且IMF分量从低频到高频分布, 其峭度值的整体趋势明显增大, 说明分量中的噪声含量所占比重越大峭度值越大。

1.4 小波变换

小波变换(Wavelet Transform)[19]是在短时傅里叶变换的基础上发展起来的一种信号时频分析方法, 适合分析非平稳信号。小波去噪的本质是根据不同频带上的信号和噪声的小波分解系数强度不同的特点, 保留原信号的小波分解系数, 去除噪声在各频带上的小波系数, 最后再将处理后的系数进行小波重构, 得到去噪后的重构信号。

目前, 小波变换主要分为以下几种方法：

1) 模极大值小波去噪方法；

2) 小波阈值去噪法[19-20]；

3) 平移不变量法；

4) 基于各尺度下小波系数相关性去噪(屏蔽去噪法)。

笔者选用小波自适应阈值去噪, 选择合适的小波基函数和分解层数是小波阈值去噪的关键, 选取Daubechies系列中的db5小波基进行5层分解, 然后对分解后的系数进行阈值处理, 最后将阈值处理后的小波系数进行重构得到去噪信号。小波阈值去噪的优点是计算简单且快速, 算法易实现, 去噪效果较好, 在实际中有较为广泛的应用。

在实际信号处理中, 有用信息一般包含在低频信号中, 而噪声信号多为高频信号, 利用相关系数和峭度值筛选出VMD算法分解出的高频模态, 将其进行小波变换就可起到信号去噪的作用。

1.5 改进的VMD算法

通过对以上几种方法的研究, 笔者将VMD算法与相关系数和峭度结合选取有效分量, 经过比较其比结合单一方法更加准确。虽然大多数声信号的主要特征集中在低频段, 但将相关系数较小或峭度较高的高频分量直接滤除会损失掉高频部分的有效信息。故笔者提出基于相关系数、 峭度和小波变换的VMD改进算法,算法流程如图1所示。

图1 VMD改进算法流程图Fig.1 Flow chart of VMD improved algorithm

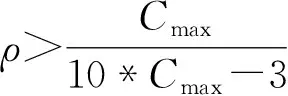
2 仿真试验与结果分析

为验证笔者提出算法的有效性, 选取各分量为2 Hz、576 Hz、6 912 Hz 3个频段的余弦信号作为原始信号并加入噪声强度为0.1的高斯白噪声进行仿真分析, 即

fn(t)=cos(4πt)+0.5cos(1 152πt)+0.05cos(13 824πt)+μ

其中μ为加性高斯白噪声。

图2为不含白噪声的原始输入信号, 图3为加入高斯白噪声后的复合信号。

图2 不含白噪声的原始输入信号 图3 加入噪声的复合信号 Fig.2 Original input signal without white noise Fig.3 Composite signal with noise

根据VMD分解经验, 选取K=4, VMD分解后的IMF分量如图4a～图4d所示。

图4 VMD分解得到的IMF分量Fig.4 IMF components derived from VMD decomposition

由式(9)计算VMD分解后得到的各个IMF分量的相关系数值, 如表1所示。

表1 各IMF分量的相关系数

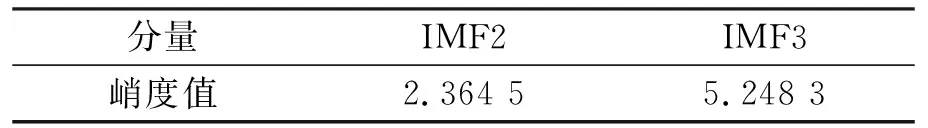
表2 剩余IMF分量峭度值

由表2判断出IMF2峭度值小于设定的峭度阈值4, 故保留IMF2分量作为峭度值筛选出的有效分量； 接着将峭度值大于4的IMF3分量进行小波阈值去噪处理, 选取db5小波基进行5层分解, 对分解后的系数进行阈值处理, 将处理后的小波系数进行重构滤除噪声, 最后将去噪后的分量与根据相关系数和峭度选出的有效分量进行重构。计算笔者改进算法和VMD与相关系数、 VMD与小波、 峭度、 豪斯多夫距离、 互信息、 小波去噪的重构信号的信噪比和均方误差进行对比, 结果如图5和图6所示。

由图5可以看出, VMD与豪斯多夫距离、 互信息、 小波去噪算法对信号去噪后的信噪比分别为6.870 2 dB,6.811 5 dB,6.700 1 dB, 而笔者提出的改进VMD算法可以比较明显提高信号的信噪比, 达到了20.084 9 dB； VMD与相关系数、 峭度和小波变换单独结合的算法对信号进行去噪, 信号信噪比分别为18.452 0 dB,18.953 4 dB和19.783 9 dB, 均低于笔者改进算法。

由图6可以看出, VMD与豪斯多夫距离、 互信息、 小波去噪算法对信号去噪后计算的均方误差结果分别为0.359 6,0.362 1,0.366 8, 笔者改进算法的均方误差最小, 为0.078 5； 将VMD与相关系数、 峭度和小波变换单独结合的算法对信号进行去噪计算出的均方误差分别为0.094 8,0.089 5,0.080 4, 均大于笔者算法计算的均方误差。根据图5,图6的对比结果, 可以看出笔者改进的VMD算法结合了3者的优点, 得到了较为理想的去噪效果。

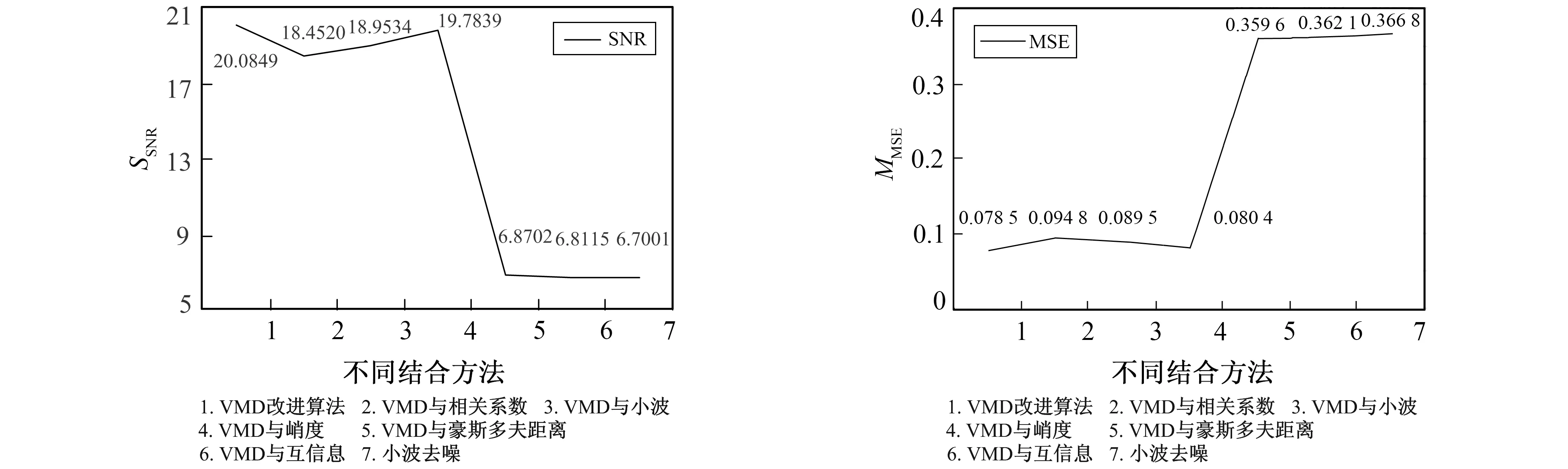
图5 SSNR对比图 图6 MMSE对比图 Fig.5 SSNR contrast diagram Fig.6 MMSE contrast diagram

3 管道泄漏信号检测与分析

笔者研究所采用的管道数据是从天然气管道泄漏检测实验室采集的, 其管道总长160 m, 管径为DN50, 管壁厚为20 mm, 管道内可以实现气体和液体的运输。管道上设有多个泄漏点用于仿真现场管道的泄漏, 并可通过监控台对管道的相关参数进行监控, 实验室管道泄漏检测系统如图7所示。试验利用Labview编程环境, 借助NI公司的数据采集板卡, 分别利用采样频率1 kHz,5 kHz,10 kHz进行数据采集, 将数据采集卡分别与两个压电式声波传感器相连, 并利用计算机完成数据采集。图8为实验室采集到的泄漏数据, 本次实验截取的长度为2 048个采样点。

a 天然气管道 b 控制台图7 实验室管道泄漏检测系统Fig.7 Pipeline leakage detection system in Laboratory

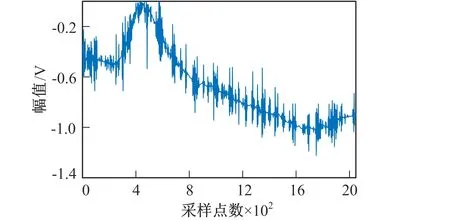
图8 管道原始信号Fig.8 Pipeline original signal

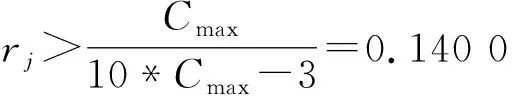
表3 各个IMF分量的相关系数

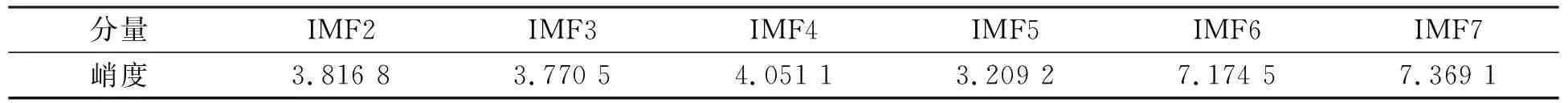
表4 剩余IMF分量的峭度值

由表4可以看出, IMF2、 IMF3和IMF5分量的峭度小于设定的峭度阈值4, 将它们保留作为峭度值筛选出的有效分量； 将IMF4、 IMF6和IMF7分量进行小波阈值去噪处理, 将去噪后的分量与根据相关系数和峭度选出的有效分量进行重构, 并计算重构信号的信噪比和均方误差作为性能评价指标。

计算笔者改进算法和VMD与相关系数、 小波、 峭度、 豪斯多夫距离、 互信息以及小波去噪的管道重构信号的信噪比和均方误差进行对比, 结果如图9和图10所示。

图9 SSNR对比图 图10 MMSE对比图 Fig.9 SSNR contrast diagram Fig.10 MMSE contrast diagram

由图9可以看出, VMD与小波结合算法、 峭度结合算法、 小波去噪的重构信号信噪比分别为17.999 6 dB,17.154 0 dB,11.024 6 dB,笔者改进的VMD算法重构信号信噪比较高, 为18.290 2 dB, 而VMD与相关系数结合算法、 豪斯多夫距离结合算法、 互信息结合算法选取的有效模态均为IMF1, 故重构信号的信噪比均为13.511 0 dB。由图10可以看出, VMD与小波结合算法、 峭度结合算法、 小波去噪的重构信号的均方误差分别为0.036 2,0.039 9,0.080 7, 均高于笔者算法的0.035 0, VMD与相关系数结合算法、 豪斯多夫距离结合算法和互信息结合算法选取模态相同, 均方误差均为0.060 6, 均高于笔者算法。

根据图9、 图10的SNR和MSE的对比结果实验, 验证了笔者提出的VMD改进算法能提高信号的信噪比, 降低均方误差, 能较好地处理复杂的管道信号, 验证了在管道泄漏检测中的有效性。

4 结 语

鉴于VMD算法分解后的有效模态分量选择比较困难的问题, 笔者提出了一种改进的VMD算法, 将VMD算法与相关系数和峭度结合选出有效模态分量, 通过小波变换去除剩余分量的噪声, 将有效模态分量和去除噪声后的剩余模态分量进行重构, 可以减少高频段有用信息的丢失, 并能较大程度地去除信号在管道传播中混入的噪声。通过仿真信号和实验室管道采集信号进行试验, 与其他算法相比, 笔者提出的算法在信号去噪方面有着较好的优越性, 并且在管道泄漏检测方面有着较好的前景。