基于Excel的单摆实验数据处理①

王 鹏 张永才

(江苏省句容高级中学,江苏 镇江 212400)

1 引言

单摆测重力加速度是基础物理实验中一个经典力学实验。[1-4]近年来,物理教学工作者对此实验进行了深入的研究,包括单摆实验装置的改进、实验设计的优化与创新、实验数据与误差分析的计算机处理等。[5-11]本文基于单摆实验实测数据,应用Excel软件进行散点图绘制和相关系数检验,采用线性拟合计算南京地区的重力加速度,并与列表法和逐差法进行比较。同时,在理想单摆模型的基础上,我们引入了单摆修正项δ,[12,13]对3种数据处理方法的g值计算进行了角振幅修正。

2 实验原理与数据记录

2.1 单摆模型

在一根不可伸长且质量不计的细线下端悬挂一个小球,上端固定。当小球的直径远小于细线的长度时,可把小球看作是一个质点。如果把悬挂的小球自平衡位置拉至一边保持摆角θ<5°,小球会在平衡位置附近作周期性摆动,即做简谐运动，这种装置称为单摆,其受力情况如图1所示。

图1

2.2 单摆实测数据

当单摆的线长L从50.0cm以5.0cm为步长增加到85.0cm时,分别测量出每个摆长所对应的单摆摆动时间t，实验中注意保证摆球速度方向与重力方向共面,防止出现圆锥摆运动。为了减小计时误差,取摆角θ=4°，测量周期时从平衡位置开始计时,每次测量20个周期,多次测量取平均值，实验数据如表1所示。

表1

3 实验数据的处理

3.1 用列表法计算g值

表2

3.2 用逐差法计算g值

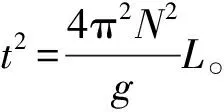
3.3 应用Excel软件绘制单摆的L-t2直线，拟合线性方程

图2

选定图2中的散点图,点击右键选择下拉菜单中的“添加趋势线”,选定对话框中的“线性、显示公式与显示R的平方值”3项,Excel软件就会得到单摆实测数据的L-t2线性拟合直线(图3)。[16]在拟合出直线的同时,软件也会给出拟合的线性方程Y=0.00061X-0.00225、相关系数R2等。

图3

3.4 三种数据处理的结果比较

3.4.1 计算结果的准确性

从表3中可以看出,用Excel软件处理实测数据,计算重力加速度g值更加接近理论值g=9.7949m/s2,相对误差较小。列表法计算重力加速度g值产生了较大的误差,是因为实验数据的取样个数对处理结果会产生较大影响,没有Excel软件拟合和逐差法那样准确。

表3

3.4.2 处理过程的高效性

Excel软件处理只需将数据输入Sheet工作表中,选择合适的拟合函数,就可快速准确地计算出结果,而列表法与逐差法都需通过计算才能得出实验结果。在数据量较大时,列表法与逐差法需要耗费较长的时间,且容易引入误差。

4 角振幅对实验结果g值的影响

表4

结合表4中的数据,我们发现引入修正项δ后,3种数据处理方法的计算结果都更加接近理论值,且相对误差均有一定的减小。

5 结语

本文利用Excel软件对单摆实验数据进行线性拟合处理,通过图像的斜率计算了南京当地的重力加速度g值,并与传统的平均值法和逐差法进行比较。计算结果表明：利用Excel软件处理实验数据,可以有效地提高数据处理的准确性。同时,引入单摆修正项δ后,3种数据处理方法的g值计算结果都更加接近理论值,且相对误差有一定程度的减小。因此,随着实验仪器的改进和计算机分析数据能力的提高,运用正确的实验数据处理方法可以有效减少误差。