指向高中生物理概念形成的认知分层进阶教学——以“惯性概念”的形成和运用为例

李旭斌 陈晓陆 郑朝阳

(中国人民大学附属中学朝阳学校 北京 100028)

1 问题的提出

《普通高中物理课程标准(2017年版)》指出：“物理观念”是从物理学视角形成的关于物质、运动与相互作用、能量等的基本认识；是物理概念和规律等在头脑中的提炼与升华；是从物理学视角解释自然现象和解决实际问题的基础.学习好物理概念是形成正确物理观念的前提，由于物理概念本身存在抽象、高度概括的特点，学生对概念的学习往往注重内容的记忆，而不善于理解概念；在运用学习过的概念分析新问题时，时常遇到困难.例如，笔者通过课前访谈发现，高一学生通过初中阶段的学习能够说出“力不是维持运动状态的原因，物体运动状态的改变需要力”，但对“推即动、不推即停”现象缺乏进一步思考，并且对于陌生情境(例如光滑水平桌面上做匀速圆周运动的钢球在细绳突然断裂后的运动方式的判断等)，不能很好地运用“惯性是维持物体运动状态的原因”进行分析.

学习进阶成为近几年国内学者研究的热点之一.郭玉英教授于2016年提出，学习进阶的起点是学生的前认知，终点是期望达到的教学目标，学生的学习进阶过程要经历从起点到终点一序列的中间发展阶段，并提出了“经验”“映射”“关联”“系统”“整合”的概念进阶模型，从“整合与发展”大的方向，建构统一的概念体系，在此基础上设计合理的学习进阶，以促进学生科学素养的连贯发展.

一线教师在物理概念或物理规律教学中，如何借鉴“概念进阶层级模型”，辅助学生理解并形成正确物理概念，同时运用概念分析和解决新问题，是一个值得研究的方面.

2 基于认知进阶的分层教学设计

高中学生认知发展特点可以概括为“由感性到理性”“由具体到抽象”“由简单到复杂”.结合高中生认知发展的特点及“概念进阶层级模型”，笔者针对物理概念或规律的教学，设计了如下的认知进阶层级模型(表1).

表1 物理概念或规律的认知进阶层级模型

3 教学实践

3.1 “惯性概念”认知层级划分与进阶教学设计

以《普通高中物理必修第一册(人教版)》的第四章第1节“牛顿第一定律”为例，本节课主要围绕“牛顿第一定律(惯性概念)”“惯性与质量”展开教学，下面以“惯性概念”建立为例，进行有关认知层级进阶的教学实践.

有关“惯性概念”的认知层级划分与进阶教学设计如表2所示.

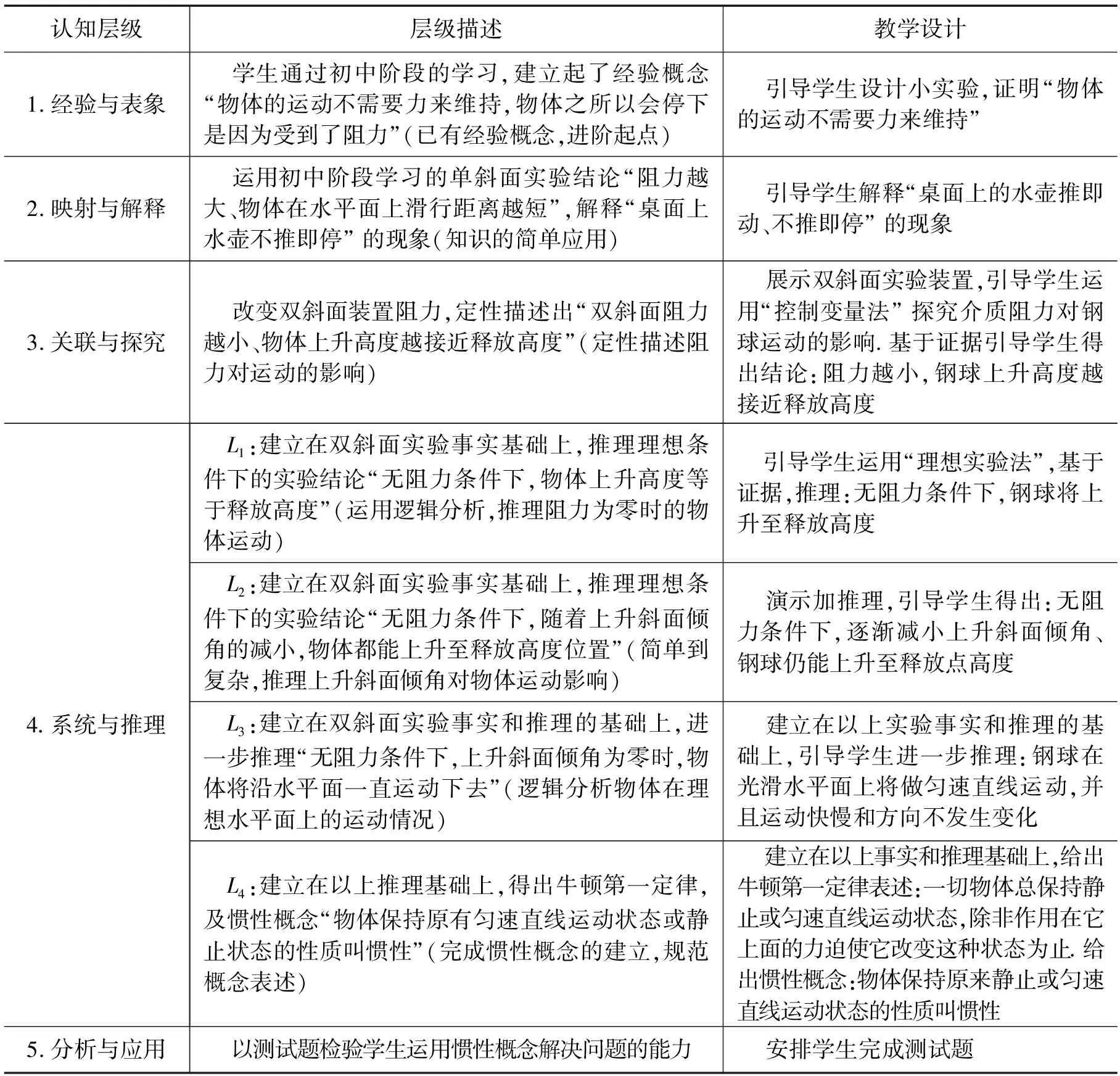
表2 “惯性概念”认知层级划分与进阶教学设计

3.2 “惯性概念”认知分层进阶教学实施

教师活动1：引入亚里士多德观点，提出问题，“如何设计实验证明物体的运动不需要力维持？”

学生活动1：通过分组讨论，运用已有经验概念和对生活现象的观察，举例“水平地面上滚动的足球”“人蹬滑板车，撤去蹬力，人和车仍然能够运动一段距离”等，论证“物体的运动不需要力维持”.

教师活动2：提出问题，“如何正确解释桌面上的水壶，‘推即动、不推即停’的现象？”

学生活动2：联想初中阶段学习过的“阻力对物体运动影响”实验结论，说明水壶不推即停，是因为水壶和桌面之间的摩擦很大，水壶在撤去推力后运动的距离很短，肉眼无法观察.

教师活动3：通过以下双斜面装置(图1)，引导学生2人一组，通过分组实验探究“介质阻力对钢球运动的影响”，引导学生明确实验的自变量是介质阻力，因变量是钢球爬升高度，控制变量是钢球释放高度，无初速度自由释放.

图1 双斜面装置

学生活动3：设计实验操作方案，将钢球从乳胶管左侧端口无初速度自由释放，观察钢球爬升高度，并用标签纸记录下这一高度；接着，通过往管里加少量水增大介质阻力，进行相同的操作；最后，分析钢球在弧形轨道中的受力，考虑到钢球重力是恒定的，有效减小阻力的方法是让钢球沿弧形轨迹运动的过程中不与乳胶管接触，实现的方法是用细绳对钢球的拉力Ft“等效替代”弧形轨道对钢球的支持力Fn，即通过单摆实现钢球沿弧形轨道运动过程中仅受空气阻力，由此减小钢球运动过程中的介质阻力，观察并记录钢球爬升高度.得出实验结论“介质阻力越小，钢球上升高度越接近释放高度”.

教师活动4-1：提出问题，“在无任何介质阻力的理想条件下，钢球最后将爬升至什么位置？”

学生活动4-1：建立在活动3的实验事实基础上，运用“理想实验法”，通过逻辑推理分析得到“无介质阻力条件下，钢球将爬升至释放高度”.

教师活动4-2：通过以下牛顿第一定律演示仪装置(图2)，引导学生推理无阻力条件下钢球运动位置，逐渐减小左侧上升坡面倾角，引导学生推理钢球运动情况.

图2 牛顿第一定律演示仪

学生活动4-2：根据“理想实验”，运用逻辑推理得到“在无阻力条件下，每次减小上升坡面倾角，钢球均能爬升至释放高度”.

教师活动4-3：引导学生推理在无阻力条件下，上升坡面倾角为零时，钢球的运动情况.

学生活动4-3：运用逻辑推理得到“钢球将一直运动下去，且运动快慢和方向均不改变，钢球做匀速直线运动”.

教师活动4-4：给出牛顿第一定律，即惯性定律，完成惯性概念的建立.

学生活动4-4：将建立的正确认知与书本概念的规范表述相对应.

3.3 对照班“惯性概念”教学实施简介

教师活动1：演示实验现象“水壶推即动，不推即停”，引出亚里士多德“物体运动需要力维持”的观点.

教师活动2：通过问题“伽利略是如何证明物体运动不需要力维持呢？”引导学生通过图2装置探究阻力对钢球运动的影响.让一个小球沿斜面从静止状态开始运动，小球将“冲”上另一个斜面；如果没有摩擦，小球将到达原来的高度；如果第二个斜面倾角减小，小球仍将到达原来的高度，但是运动的距离更长.由此可以推断，当斜面最终变为水平面时，小球要到达原有高度将永远运动下去.这说明，力不是维持物体运动的原因.

教师活动3：引出笛卡尔观点，如果运动中的物体没有受到力的作用，它将继续以同一速度沿同一直线运动，既不会停下来，也不会偏离原来的方向.

教师活动4：引出牛顿第一定律的表述，并且指出牛顿第一定律中物体这种保持原来匀速直线运动状态或静止状态的性质叫做“惯性”.

4 实验研究

4.1 测试目的与被试选取

为检验基于物理概念或规律的认知进阶教学，对辅助学生物理概念形成和规律认知的成效，笔者对实验班和对照班学生进行了后测，其中比较典型的两道测试题，分别考查学生对惯性概念的理解情况和运用情况.测试题1跟踪学生概念建立过程中“根据实验获取事实证据”“基于事实证据进行逻辑推理”两个方面能力的发展情况，这两个方面是完成惯性概念建立的重要发展阶段；测试题2以“分析和应用”的层级要求，考查学生运用惯性解决新问题的能力.

本研究选取本校2019级在读高一学生作为被试，本校高中物理教学为走班教学，并且依据学生的能力水平，将学生分为从高到低A，B，C，D 4个层次共8个班级，同层次有两个班，本文选取同一教师所教授的B1(33人)、D1(20人)为实验班，B2(29人)、D2(22人)为对照班.

4.2 测试题选取与考查点设计

本文选用的两道测试题分别反映学生对惯性概念的理解和运用情况.测试题1由北京高考题改编，考查学生“惯性概念”形成过程中关键认知层级的达成情况，学生在“系统与推理”层级下，是否能够按照逻辑次序以双斜面实验事实推理光滑水平面上的运动情况，以评价学生对惯性概念的理解情况；测试题2是一道易错题，考查学生运用“惯性概念”分析解决问题的能力.

【测试题1】如图3所示，某同学在探究斜面阻力对钢球运动影响的实验过程中，通过某方面的实验操作，发现小球沿斜面上升的位置依次为1，2，3，由此通过推理得出的最直接结论是( )

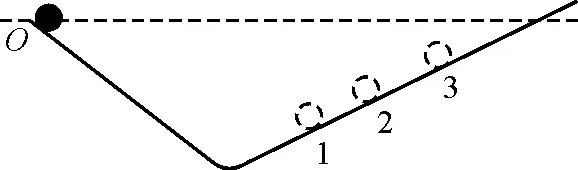
图3 测试题1题图

A.小球所受阻力越小，小球沿斜面右侧爬升高度越接近释放高度

B.如果斜面光滑，小球将上升到与O点等高的位置

C.随着右侧上升坡面倾角的减小，小球将仍然上升到与O点等高的位置

D.如果小球不受力，它将一直保持匀速直线运动状态或静止状态

【测试题2】如图4所示，在一辆表面光滑的小车上，有质量分别为m1和m2的两个小球(m1>m2)随车一起匀速运动，当车突然停止时，如果不考虑其他阻力，设车足够长，则两个小球( )

图4 测试题2题图

A.一定相碰

B.一定不相碰

C.不一定相碰

D.无法判断，因为不知道小车运动方向

4.3 研究数据与分析

第1题的正答率如图5所示.

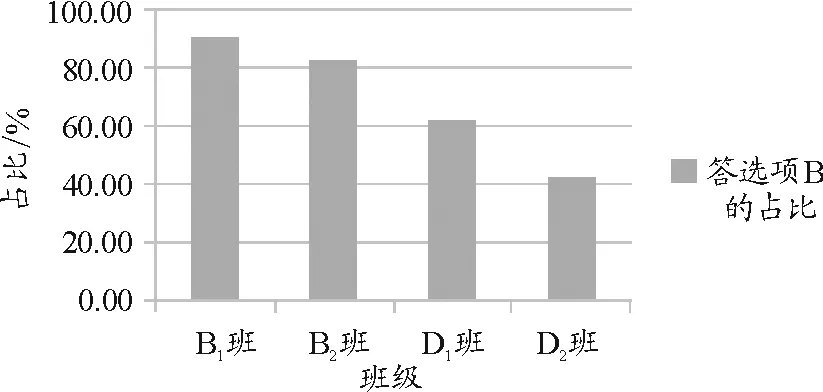
图5 测试题1正答率

同层次实验班表现优于对照班，在“系统与推理”层级下，实验班基于实验事实推理理想条件下实验结论的逻辑清晰程度更高，对“惯性维持物体运动状态”的深入理解更到位.

第2题正答率如图6所示，该题正答率能够体现出明显的班级层次差异性，同层次实验班学生运用“惯性维持物体运动状态，物体运动状态改变需要力”解决问题的能力优于对照班.

图6 测试题2正答率

5 结论

本文通过实验研究发现，基于认知进阶的分层教学设计对引导学生“惯性概念”的形成有较好的成效，并且对提升学生运用“惯性概念”分析解决实际问题的能力起到积极作用.