初中物理科学推理教学的研究*

李宝银

(海安市紫石中学 江苏 南通 226600)

何为科学推理？目前学界的共识：科学推理是个体思维能力发展到一定程度之后具有的推理类型，个体进行科学推理一般采用演绎推理和归纳推理，个体应用科学推理进行假设检验或问题解决.基于这样的共识，笔者在文献研究的基础上，结合自身的教学实践，介绍科学推理的教学.

1 注重科学推理教学的缘故

1.1 科学推理能力是物理的学科能力

文献研究成果表明，科学推理是重要的学习理解能力，行为表现：在已有知识基础上进行逻辑推理，获取新知识.科学推理又是重要的应用实践能力，行为表现：一是基于物理问题的描述与分析，依据已有知识，进行合理推理，并得出结论；二是基于推论，结合具体物理问题情境，对事物或过程的发展做出合理的猜想与假设[1].《江苏省义务教育学科核心素养·关键能力框架》(试行)中认定，科学推理是学生在进行物理知识学习过程中表现出来的能力，是初中物理的关键能力[2].

1.2 发展科学推理能力是物理的课程目标

《普通高中物理课程标准(2017年版)》界定的物理学科核心素养，主要有“物理观念”“科学思维”“科学探究”和“科学态度与责任”4个方面的内容.“科学思维”涵盖“模型建构”“科学推理”“科学论证”和“质疑创新”4个要素[3].对“科学推理”的要求是运用科学思维方法，从定性和定量两个方面对相关问题进行科学推理、找出规律、形成结论.

《标准》对物理课程在高中的地位与作用的表述：高中物理是自然科学领域的基础课程，旨在落实“立德树人”根本任务，进一步提升学生的物理核心素养，为学生的终身发展奠定基础，促进人类科学事业的传承与社会的发展.

前面的阐述表明，高中物理和初中物理不是相互孤立的而是彼此衔接的，将要“出生”的“义务教育物理课程标准”中注定有科学推理方面的教学要求，即发展科学推理能力也是初中物理的课程目标.

2 学生科学推理能力的特征

当前学界主要采用LCTSR科学推理能力测试量表，从守恒推理、比例推理、控制变量推理、相关推理和假设演绎推理等维度对学生科学推理能力进行测量.研究成果表明，当前初中生科学推理的主要特征有以下几个方面.

2.1 科学推理能力发展呈线性上升的阶段

国内外相关研究成果表明，个体生理发育对学生科学推理能力的发展具有显著的影响[4].二年级到七年级学生的生理发育尚未达到科学推理相应的认知阶段，此阶段学生科学推理能力没有显著发展，不需要也不能对学生的科学推理提出过多过高的要求.七年级学生已经渐渐具备科学推理发展所需要的生理基础，学生的科学推理能力呈明显上升趋势，即初中阶段应该注意学生科学推理能力的培养，在物理课上必须有发展科学推理的教学目标.

2.2 科学推理能力高水平学生的比例很小

某地初三学生的测试成绩统计：满分24分的测试工具，测试的平均成绩为15.9分(得分率66%)，5～12分的学生数占17.8%，13～20分的学生数占69.6%，21～24分以上的学生数只有12.6%[5].

数据表明，初三学生的科学推理能力整体水平位于较高水平，大部分学生的科学推理能力位于中等水平，科学推理能力达到高水平的学生人数不多.不言而喻，初中学生在科学推理能力的发展方面尚有很大的空间，在概念、规律的教学中需要强化科学推理的训练.

2.3 科学推理能力不同维度的发展不平衡

科学推理能力中各个维度的发展不平衡，控制变量推理、相关推理、假设演绎推理的水平落后于科学推理的整体水平，远远落后守恒推理和比例推理的水平.究其原因，近十几年来考试的压力导致“先学后教”“导学案”等课堂教学改革的泛滥，很多教师无视这些改革的适用范围，将其当作制胜的法宝,在教学中盲目而大量地运用.

例如，“导学案”引领的课堂，学生往往是根据“导学案”从教材中寻找概念和规律，然后通过反复的训练与强调达到掌握的目的.

守恒推理、比例推理具有相对稳定的计算形式或推理范式，在这样的反复训练和强调之中,即使学生生理发育尚未达到相应的层次,其能力水平也会获得顺利的提升.

控制变量推理和相关推理能力是在建构概念和探究规律的过程中生成的能力，这些教学行为省略了学生归纳概念、总结规律的思维过程，控制变量推理、相关推理因缺乏相关的体验和感悟，没有获得应有的发展，导致其水平层次不高.

2.4 控制变量推理能力的发展不完善

对此结合“2018年江苏省基础教育质量监测”两道测试题及其相关的数据进行说明.

【第1题】在“探究敲击铜管发声的频率与管子长度、直径关系”的实验中，小明选取管壁厚度相同，长度和直径不同的3根铜管，将它们用细线悬挂，敲击后，测出各自发出声音的频率，数据如表1所示.

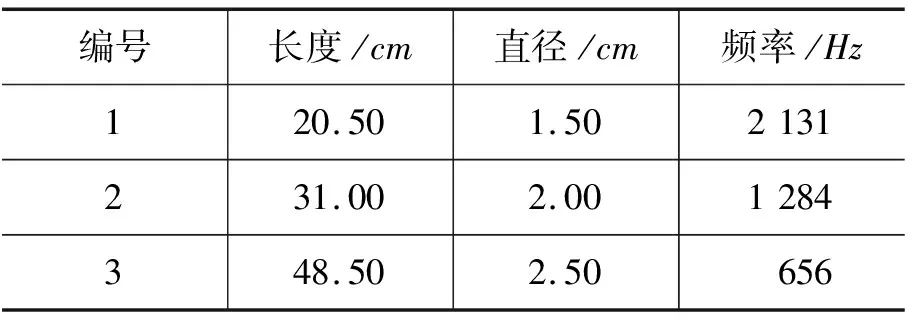
表1 3根铜管发出声音的频率

根据小明的实验数据( )

A.只能得出频率随长度增加而减小的结论

B.只能得出频率随直径增加而减小的结论

C.选项A和B的结论都能得出

D.选项A和B的结论都不能得出

【第2题】如图1所示，柱形容器中装有油和水两种液体，P点位于油和水的分界面上，Q点位于容器底部.已知柱形容器中液体对容器底部的压力等于容器中液体的总重.若将容器中的油和水均匀混合，且混合后的总体积保持不变.则混合后( )

图1 题2情境图

A.P点的压强变小 B.P点的压强变大

C.Q点的压强变小 D.Q点的压强变大

两道题的相同点，推理情境都是基于多因素变量，采用的都是控制变量推理，推理情境中涉及到变量的数目相同.第1题涉及到频率、长度和直径3个变量.第2题的难点是判断P点压强的变化情况，由于初中物理中没有涉及到液体压强公式，对P点压强变化情况，实际是控制深度不变，判断压强随密度的变化情况，涉及压强、深度和液体密度3个变量.

两道题的相异点，主要反映在推理情境的设置上，呈现出不同的推理思路，第1题是通过表格和文字点明，需要控制的变量显而易见，这种思路是学生较为熟悉的控制变量推理.第2题是针对实际问题通过观察思考，判断容器中液体密度和P点深度的变化情况，变量之间的关系较为隐藏，推理情境较为复杂，具有实际物理问题的特征.

对两道题进行数据统计，全省范围内依据统计学原理从被测对象的总体基数中分层随机抽出47 000多名学生，测试于进入初三当年的10月份进行，测试结果如表2所示.

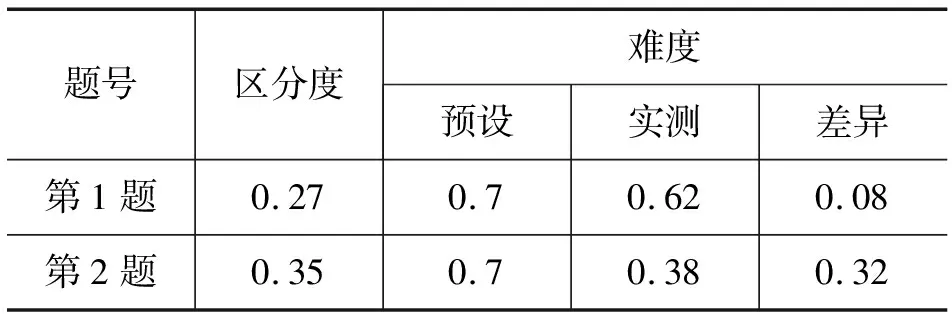
表2 测试结果

两道题的区分度较高，实际测试的难度都低于命题组预设的难度，尤其是第2 题两个难度有着显著性的差异.相对简单的推理情境，大部分学生能较好地运用控制变量推理解决问题；相对复杂的推理情境，很多学生就不能很好地运用控制变量推理解决问题.

可见，通过初二的学习，学生控制变量推理的水平没有达到课程目标的要求，推理思维的深度、广度还不够，控制变量推理能力的发展不完善.

3 发展科学推理能力的思路

根据初中学生科学推理能力的特征，科学推理教学的重心应该落实在假设演绎推理、控制变量推理和相关推理3个维度上.对控制变量不仅要运用其归纳概念、总结规律，而且要运用其分析实际问题，并依据物理知识或经验推理其结论.为此，教学过程中应该注意下列几点.

3.1 精选教学策略

精选体现在根据教学内容和教学目的选择恰当的教学方法和思路.

例如，笔者对教材中重点的探究，采用“探究在前，教材在后”的教学思路[6]：探究在前的核心就是探究活动提前到学生阅读教材之前，精心创设有利于探究学习的情境，把握时机进行适度、适时的引导、点拨，让学生在没有教材的前提下，开展探究性学习；教材在后的内涵就是阅读教材延迟到探究活动结束之后，运用适当的问题带领学生，结合教材对知识进行梳理、内化，完善其知识结构.

没有教材的暗示和引领后，学生只有针对情境进行推测才能提出合理的猜想与假设；只有基于实验现象和数据才可能推理出可靠的实验结论；才有机会基于探究方案预测可能的实验现象或数据；……显然，“探究在前、教材在后”的思路，有益于控制变量、假设演绎和相关等维度的科学推理能力发展.

3.2 重视因果推理

概念、规律教学时，教师把握学生的特点，多些追问的细节，抓住学生的思维点，从表面深入到本质，从具体上升到抽象，帮助学生在物理事实和结论之间架桥.

例如，因教材的暗示，针对图2所示的实验，学生一般都能回答液化时气体会放热，然而很多学生往往不知道“放热”的结论从何而来.这时教师不妨问，你们是根据什么现象总结“气体液化要放热”的？引发学生道出“瓶口附近没有出现白气，只有瓶口上方靠近温度较低的金属盘的地方才出现白气”.

图2 气体液化实验

再如，在探究平面镜成像的规律时，学生根据玻璃板后面的蜡烛和玻璃板前面蜡烛的像重合，容易回答结论“像和物体大小相等”.事实上，学生往往没有顾及到为什么？这时教师就需要适当的诱导，让学生知道玻璃板后面的蜡烛和前面蜡烛的像重合，表明蜡烛的像和后面的蜡烛大小相等，再考虑到前后两个蜡烛相同，推理出“平面镜所成的像和物体大小相等”.

因果推理使学生理清了物理现象与物理结论的关联，真正达到了知其然，也知其所以然，如果经常这样教学，学生基于证据进行推理的能力肯定会有长足的发展.

3.3 用活控制变量

不容置疑初中物理对“控制变量”的教学非常重视，然而某些不当的教学行为导致很多学生没有理解和掌握控制变量推理的内涵，而在僵硬地运用控制变量.

例如，针对如图3所示的情境，学生往往认为因深度不相同，而不能得出“深度相同时，液体的密度越大，压强越大”的结论.事实上，如果已经有“液体压强随深度增加而增大”的结论，由图示情境可以得出结论——深度相同时，液体的密度越大，压强越大.因为，如图所示的情境，压强计在盐水中的深度小于在酒精中的深度，而盐水产生的压强已经大于酒精产生的压强，假设压强计在盐水中的深度和酒精中深度相同，则盐水产生的压强会更大.

图3 探究液体压强与深度关系

探究教学中，教师要注意运用这类拓展性的情境来训练学生的科学推理，使其真正把握控制变量的精髓，同时发展假设演绎推理的能力.

目前初中物理教学中使用的训练材料以习题为主，已经把实际问题的一些次要细节、非本质的联系舍去，没有物理现象或事实作为背景，甚至完全脱离于物理现象，习题训练起来的科学推理能力，往往不容易迁移到实际问题之中.

例如，如图4所示，将等体积的热汤，分别倒在一个陶瓷汤盆和一个单层的不锈钢碗里，将它们放在室内同一处.你认为是盆还是碗里的汤会凉得快些？请说明你的理由.

图4 判断热汤变凉快慢

这道题最初出现在江苏省基础教育质量监测试卷中，当年只有0.8%的学生根据蒸发、热传导的知识，运用控制变量进行推理，给出“无法判断”的结论，且理由基本合理；68.3%的学生根据蒸发(或热传导)的知识，给出“盆(或碗)里的汤会凉得快些”的结论.近年，两次将其放在招聘教师的试卷中，能从蒸发、热传导两方面考虑的教师都不到10%.

显然，物理教学过程中，注意运用这样的实际物理问题来训练学生运用控制变量推理的能力也就显得十分重要.

3.4 指点方法技巧

毫无疑问，科学推理不是盲目的瞎想，而是有章可循的，这里“章”就是方法和技巧.前面针对图3所示情境的讨论，是假设深度相同基础上的科学推理，如果离开“假设”学生很难将其表述明白，这里“假设”就是科学推理的技巧.

根据多个变量总结规律时，如果根据实验数据证明某个变量对结论没有影响，后续的讨论就不在此变量上纠缠，这也是科学推理的技巧.

例如，探究影响浮力大小的因素时，从实验现象中已经发现浮力大小与物体浸入的深度无关，总结浮力与密度的关系时，不需要考虑物体所在的深度.实验结论应该表述“排开液体的体积相同时，液体的密度越大，所受的浮力越大”，若在结论中出现“深度相同”的内容就是画蛇添足.

由实验数据总结规律时，什么时候需要画坐标图像？探究滑动摩擦力和压力的关系时，画出的坐标图像是过原点的直线，表明滑动摩擦力与压力间有什么关系？……这些推理用到的“方法”对教师而言简单又简单，对学生而言难上加难，离开教师的适时、适当指点，学生很难意识到.

最后的提醒，培养学生的科学推理能力应循序渐进，要求不能太高，速度不能过快，注重习得与养成，不拔苗助长，学生能做到的当然由他们来.