基于LSTM 的湿法烟气脱硫浆液pH 值建模

金秀章，景 昊

(华北电力大学 控制与计算机工程学院，河北 保定 071003)

0 引言

目前燃煤电厂的SO2排放量已经超过了 SO2排放总量的一半，并且呈现逐年递增的趋势。我国先后颁布的《火电厂大气污染物排放标准》和《煤电节能减排升级与改造行动计划 （2014—2020 年）》等一系列政策法规，明确指出火电厂的SO2排放浓度必须控制在 35 mg/m3以下[1]。石灰石-石膏湿法烟气脱硫技术(WFGD)是目前最有效的燃煤机组SO2控 制 技 术 之 一[2]。WFGD 工 艺 中 浆 液 pH 值 是决定烟气脱硫效率的关键参数，因此pH 值的测量需要迅速、准确。

在 WFGD 现场测量时由于环境恶劣，且 pH 值变化具有较大的惯性，导致测量时长较大，无法及时得到浆液 pH 值的准确值，对于脱硫作业十分不利。因此需要对浆液 pH 值进行预测。

pH 值测量作为非线性系统一直是研究热点[3]。利用燃煤机组的运行数据，再结合机理分析，采用实验建模的方法可以辨识出精确合理的系统模型[4]。文献[5]和文献[6]把神经网络等自适应模糊系统用于 pH 中和过程。BP 神经网络、RBF 神经网络、Elman 神经网络等方法是 pH 值建模的典型方法,但上述算法本身在时间序列的处理上并没有突出的优势。

随着技术的进步，深度学习、递归神经网络、卷积神经网络等也在 pH 值建模得到应用[7-10]。LSTM神经网络，注重数据间的时间特性，在大迟延时间序列预测中具有突出优势[11]。LSTM 神经网络的特点在于发现当前时刻数据与之前数据间的联系，利用本身具有的记忆能力，将之前数据的状态进行保存[12]，同时根据保存的信息影响后续的预测值及变化趋势。

因此，本文提出一种基于LSTM 神经网络的pH值预测模型。以某 600 MW 机组为研究对象，使用机组实际运行数据，经过机理和相关性分析，确定pH值模型的辅助变量，建立高精度的pH 值预测模型。

1 LSTM 网络

作为循环神经网络(Recurrent Neural Network，RNN)中的一个特殊情况，LSTM 与前馈神经网络不同，属于反馈神经网络的一种。RNN 中神经元的输出可以在下一个时刻作用于自身，且共享从样本序列中不同位置学习到的特征，以此减少模型中的参数数量，这一点在数据规模庞大时具有重要意义。与传统RNN 网络的区别在于，LSTM 网络结构加入了控制门的机制，结构包括记忆细胞、输入门、输出门、遗忘门四部分。LSTM 原理图如图1 所示。

图1 中，三个框分别为不同时序下的细胞状态，δ表示激活函数为sig-moid 的前馈网络层，tanh 表示激活函数为 tanh 的前馈网络层。Xt表示 t 时刻的输入，S(t)表示 t 时刻细胞的状态值，前馈网络层中的隐藏神经元个数经多次调试后，确定一个最佳值。

输入门 it的值和在t 时刻输入细胞的候选状态值，计 算 如 下 ：

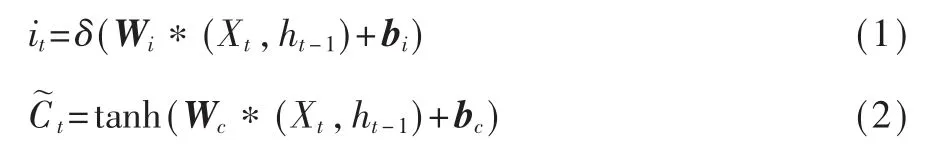
其中，Wi为输入门的权重矩阵，bi为输入门的偏置项；Wc为细胞当前状态的权重矩阵；bc为细胞当前状态的偏置项。

其次，计算在 t 时刻遗忘门的激活值 ft，公式如下：

式中，Wf为遗忘门的权重矩阵，bf为遗忘门的偏置项。

由以上公式可计算出t 时刻的细胞状态更新值 S(t)，公式如下：

计算出细胞状态更新值后，可计算输出门的值ht，公式如下：

式中，Wo为输出门的权重矩阵，bo为输出门的偏置项。

通过以上计算，LSTM 可以有效利用输入数据使LSTM 神经网络具有长时期记忆功能。

2 模型的建立

2.1 辅助变量的选择

根据 WFGD 的生产机理，pH 值的影响因素来源于两个方面，分别是燃烧侧产生的SO2总量和新鲜石灰石浆液的供应量。如果SO2总量不变，新鲜石灰石浆液供应量增加可以增大pH 值；如果新鲜石灰石浆液供应量不变，SO2总量增大可以降低pH值。因此模型辅助变量应选取与SO2总量和新鲜石灰石浆液变化有关的物理量。之后使用互信息计算浆液pH 值与生产中所涉及的物理量的相关性。选取与浆液pH 值相关性大的变量为辅助变量。因为浆液 pH 值变化惯性大，所以当前时刻浆液 pH 值受前时刻浆液pH 值的影响。最后确定总风量、总煤量、净烟气 SO2浓度、原烟气 SO2浓度、原烟气流量、空预器入口烟气氧量、空预器出口烟气氧量、炉浆液密度、新鲜石灰石浆液流量、吸收塔液位、两台氧化风机电流及5 s 前的浆液pH 值为辅助变量。

图1 LSTM 结构图

2.2 数据预处理

本文所用数据源于某燃煤电厂的历史数据。预处理包括剔除粗大值、数据中值滤波两部分。

2.2.1 粗大值处理

数据规模足够，且趋于正态分布，因此使用 3σ准则对数据进行粗大值处理。步骤如下：

(1)计算标准差 σ

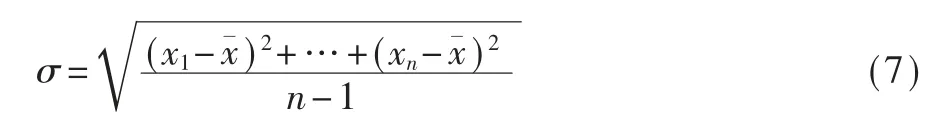
式中，xn为数据值；n 为数据个数；为数据平均值。

(2)比较数据是否满足下式要求，如果不满足则将数据剔除。

(3)重复步骤(2)，直到数据全部满足式(8)的要求。

2.2.2 数据滤波

对数据曲线中带有“毛刺”的数据滤波，可以消除噪声的影响，使数据变化更加平滑，更加接近真实数据。其中辅助变量总风量的滤波图如图2 所示。

2.2.3 时序调整

pH 值变化是一个复杂的过程，存在多变量、多耦合及迟延的问题。因此采用互信息法求辅助变量与主导变量间的时间迟延，对变量进行时序调整，进一步提高模型预测精度。

2.3 构 建 LSTM 模 型

模型以浆液 pH 值作为输出，采用三层 LSTM 神经网络建立，每层21 个神经元，优化算法为 Adam，最大迭代次数为 280，初始学习率为 0.005，在 125轮训练后乘以 0.1 来降低学习率。选用 8 700 组预处理后的数据进行仿真实验，其中6 700 组用于模型训练，2 000 组用于模型测试，数据采样时间间隔为1 s。

基于 LSTM 神经网络的 pH 值预测模型 LSTM模型结构如图3 所示。

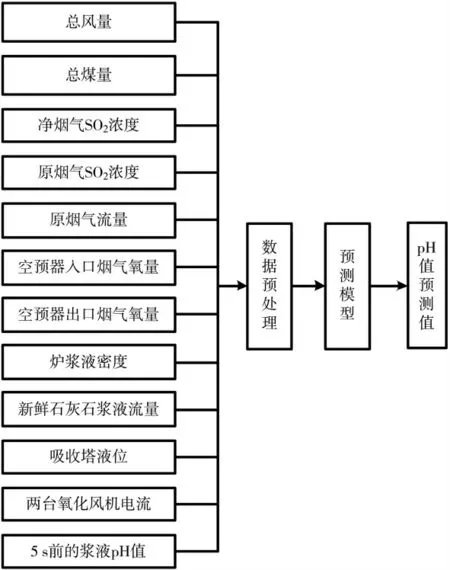
图3 LSTM 模型结构

图2 数据滤波

3 结果分析

为了便于验证模型的性能，使用LSTM 模型与BP 神经网络模型和 LSSVM 模型进行对比。模型预测值与实际值如图4 所示。LSTM 模型与 LSSVM 模型和BP 神经网络模型相比在预测趋势、预测精度方面更加具有优势。LSSVM 模型测试结果显示，在浆液 pH 值增大时，预测值下降；pH 值不变时，预测趋势反复波动。BP 神经网络模型测试结果显示，浆液 pH 值不变时，预测值反复波动；pH 值增大时，预测值没有明显的趋势变化。同时LSSVM 模型和BP 神经网络模型的预测值一直在频繁、剧烈波动，使预测精度更低。而LSTM 网络模型测试结果显示，浆液pH 值稳定时，预测值也比较稳定；在浆液 pH值急剧增加时，预测值也在急剧增加，预测值与实际值紧密跟随，且增加后迅速保持稳定。对比三个不同模型测试结果，LSTM 模型在预测精度、趋势跟随上均优于LSSVM 模型和 BP 神经网络模型，验证了LSTM 模型在数据挖掘和时间序列处理上的优势。

模型的预测误差如图5 所示。LSSVM 模型、BP神经网络模型误差较大，多次出现误差比较严重的值，且误差曲线一直存在频繁、剧烈的波动，因此LSSVM 模型、BP 神经网络模型预测不理想。LSTM模型误差最小，误差稳定在0 刻度左右，没有出现较大误差。因此 LSTM 模型测试结果最好。

为了进一步分析模型的性能，采用平均绝对误差(MAE)和均方根误差(RMSE)两个指标对各个模型进行分析，如式(9)、式(10)所示：

式中，ypi为预测值，yai为实际值。

如表1 所示，LSTM 模型与 BP 神经网络模型、LSSVM 模型相比测试结果最好。LSTM 模型与LSSVM 模型相比平均绝对误差降低了0.014 0，均方根误差降低0.016 6。本文建立的LSTM 神经网络模型与BP 神经网络模型、LSSVM 模型相比在趋势、精度、平均绝对误差及均方根误差方面均有非常大的提升，验证了LSTM神经网络在时间序列处理上的优越性，也验证了LSTM 模型在浆液pH 值预测的有效性及通用性。

表1 模型测试结果

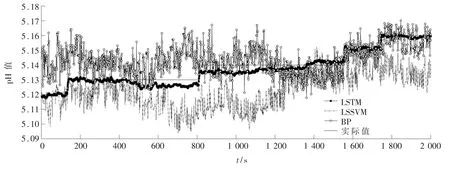
图4 模型预测值与实际值

图5 模型预测误差

4 结论

针对燃煤电厂 WFGD 过程中石灰石浆液pH 值的变化受多个变量的影响，且变量之间具有相关性和现场数据具有时序特性，本文提出了一种基于长短期记忆网络的 pH 值预测模型。首先，通过机理分析初步筛选辅助变量后进一步使用互信息确定辅助变量；然后，建立LSTM 神经网络模型；最后，使用燃煤电厂数据对模型进行测试。模型测试结果表明本文所提出的 LSTM 模型相对 BP 神经网络模型、LSSVM 模型预测精度高、泛化能力强。

需要说明的是，由于数据量有限，本研究只能归纳出高负荷状态下的浆液pH 值预测模型。然而随着燃煤电厂智能化水平的提高，电厂数据海量化和高维化已经成为必然趋势。合理使用这些数据可以进一步建立全工况的浆液 pH 值预测模型，这也是后续的研究重点。本文结果对LSTM 算法在燃煤电厂的实际应用具有一定借鉴意义。