基于离散余弦变换的轴承故障诊断方法与应用研究

郭吉祥

(中铁十一局集团汉江重工有限公司 湖北襄阳 441006)

1 引言

离散余弦变换(Discrete Cosine Transform，DCT)是和傅里叶变换相关的一种变换算法，经常在图像处理和信号处理中使用。离散余弦变换的变换核函数为余弦函数，不但具有正交变换性质，而且它的变换矩阵基向量还能很好地表征图像与信号的相关特征，因此常被认为是一种准最佳变换。近年来，已有不少学者将离散余弦变换算法应用到机械故障诊断领域，如尹丽[1]提出的采用离散余弦变换域循环维纳滤波算法对振动信号进行滤波，不仅能保证线性相位，还具有良好的滤波效果；臧怀刚[2]等提出了一种基于改进的DCT和EMD的轴承故障诊断方法，能够对轴承故障进行准确诊断；陈安华[3]等将离散余弦变换应用到列车轮对踏面损伤的检测，可快速、准确地检测出机车踏面的损伤，有效地提取列车轮对踏面损伤的特征信息；陈彦龙[4]等借助离散余弦变换(DCT)的频域能量聚集性和奇异值分解(SVD)的时域能量聚集性，对轴承复合故障信号进行预处理，实现降噪并分离频率相近的微弱故障信号；陈彦龙[5]等结合离散余弦变换(DCT)，将离散时间序列经过离散余弦变换处理成对应的系数向量，在阈值处理的基础上，重构信号有效提取出了微弱故障信息；陈彦龙[6]等将振动信号进行离散余弦变换得到频域系数，对频域系数自动分段，并对不同分段情况下的频域系数进行分析，克服了时域内相关分析受噪声影响导致诊断不准确的缺点，在含噪声情况下保证了诊断结果的稳定性、准确性；原菊梅[7]针对故障诊断特征参数的应用缺陷，提出了一种小波和余弦变换的感应电机轴承故障特征参数提取方法，并对实际感应电机轴承正常、内圈故障、外圈故障和滚珠故障的振动信号进行分析，有效地实现了电机轴承的早期故障检测与诊断；杨丽娟[8]等提出一种适用于多轴承振动信号的分布式压缩感知重构算法，通过引入离散余弦变换，实现了轴承振动信号在变换域的稀疏化和基于TSBL的重构算法，达到了多轴承振动信号联合重构的目的，解决了轴承状态监测中多传感器数据采集造成的问题。

根据离散余弦变换的能量聚集性和线性性质，以及旋转设备振动信号的循环平稳性，文献[9-10]提出了利用多个数据包数据来设计滤波器以实现对信号消噪处理的方法。该种滤波器与其它经典滤波器主要不同在于此种滤波器完全由采集信号自身得到，而不需要事先指定频域窗函数的形状、幅值和位置，克服了传统频域滤波器的某些缺陷。本文借鉴其构造滤波器思想，设计了一种基于离散余弦变换的新型滤波器，基于此提出了离散余弦变换的轴承故障信号特征提取方法，并通过模拟信号和轴承故障信号两个算例验证该方法的有效性。

2 离散余弦变换原理

1974年，由N.Ahmed、T.Natarajan和 K.R.Rao提出离散余弦变换概念以来，很快在各种信号处理领域得到广泛应用，其主要原因是离散余弦变换具有较好的能量集中特性。

假设给定一长度为N的序列x(n)，一维离散余弦变换和反变换由以下两式定义:

由于离散余弦变换具有较好的能量集中特性，故信号中不同频率特征的能量聚集分布在不同的频带，而噪声信号则在整个频带中均匀分布。另外，离散余弦变换还具有线性特性，即使是噪声污染的信号，其能量聚集特性也不会因此消失，且能很好地表征频率特征的相关信息。

3 基于离散余弦变换的特征提取方法

3.1 构造离散余弦变换滤波器

由于离散余弦变换具有一个线性性质，即:DCT(x+y)＝DCT(x)+DCT(y)，本文基于此建立一个新滤波器。假设存在m组等长度信号zj(n)，由以下两部分构成:

其中，y(n)为待处理的特征信号；wj(n)为噪声信号。一般情况下，特征信号与噪声信号互不相关。根据自相关函数的性质可知，周期性信号的自相关函数仍然是周期函数，且与原信号同周期，在采集各组信号zj(n)时，须保证各组信号中y(n)相位相同。该滤波器的构造过程如下:

(1)首先将zj(n)进行离散余弦变换，得到Fj(u)

式中，F(uy)为特征信号频域；Fj(uw)为噪声信号频域。

(2)构造滤波器

将上式中分子展开后得到:

高斯白噪声在时延为零时，具有最大的自相关值，自相关函数随着时延m趋近无穷大时，则公式(6)中后三部分趋近于零，仅保留与y(n)中特征有关的部分。于是便得到一个略去绝大部分噪声信号而保留下特征信号的窄带新滤波器。由于构造的滤波器是频域滤波器，任何一组周期信号的频域是相同的，受噪声影响后也近似相同，故可以任意选择一组信号做为处理信号。

3.2 特征提取方法

从滤波器构造过程可以看出，采集的故障振动信号需保证得到多组等长度信号同相，这可以通过控制信号采集过程来解决。例如在旋转机械平稳转动过程中采集足够长的信号，然后按照旋转周期进行等长度分割来实现；对于非平稳信号可以在保证测量条件的前提下，通过重复多次测量便可得到所需采集的故障信号。

首先通过构造仿真或采集振动信号得到待提取信号，再将待处理信号根据需要等分多组，通过进行离散余弦变换得到特征信号频域，然后根据本方法构造滤波器，进而可以从各组中任选一组离散余弦变换系数，与构造滤波器相乘，最后对所得的新离散余弦变换系数进行逆变换，从而得到去除绝大部分噪声信号的特征信号。

基于离散余弦变换的特征提取方法具体步骤如下:

(1)将采集故障振动信号或仿真信号等分M组，或者重复多次测量M组故障振动信号；

(2)将M组故障振动信号进行DCT，并用于离散余弦变换系数构造滤波器H；

(3)从各组Fj(u)中任选一组离散余弦变换系数，与构造滤波器H相乘；

(4)将经过滤波器H处理后离散余弦变换系数进行IDCT，得到特征信号；

(5)最后通过提取的特征信号进行故障分析，确定故障类型。

4 模拟仿真信号

任选取一组平稳模拟仿真信号:

其中，w(t)为[-1 1]之间正态分布的随机噪声；系数k表征噪声能量大小。

设定模拟仿真信号的采样长度为20 s，采样频率为10 kHz，然后将设定模拟仿真信号等分100组，利用离散余弦变换理论及Matlab软件构造滤波器，任选一组离散余弦变换系数，与构造滤波器H相乘后重构特征信号，即降噪信号。本文所用方法与小波变换降噪的结果进行对比，见图1～图4。其中图1为无噪声平稳信号时域图与频谱图(即k＝0)；图2为含强噪声的平稳信号时域图与频谱图(k＝15)；图3、图4分别为小波变换和本文方法降噪后的时域图与频谱图。

图1 无噪声信号时域图与频谱图

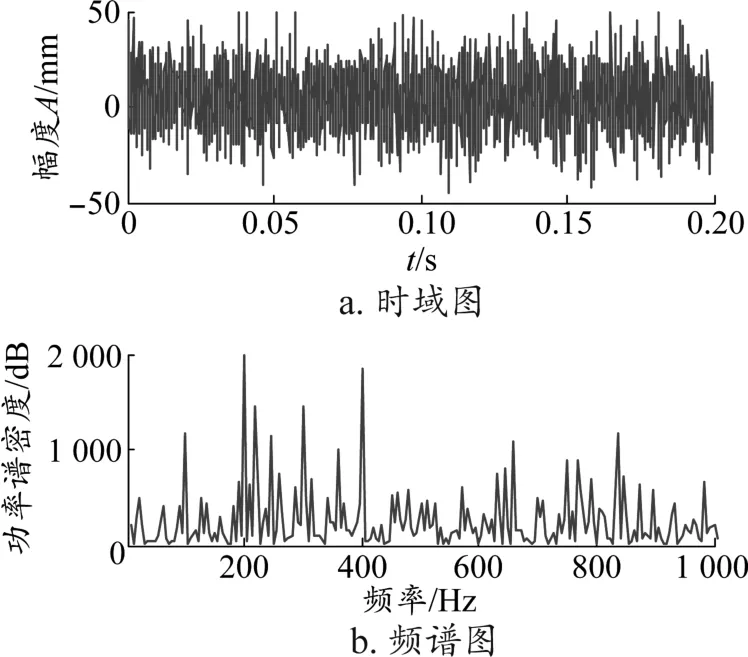
图2 k＝15时信号时域图与频谱图

图3 k＝15时小波降噪信号时域图与频谱图

图4 k＝15时本方法降噪信号时域图与频谱图

从图2～图4可知，当噪声相对较强时，小波变换降噪的时域图与模拟仿真信号时域图相比，分辨不出信号的波形；而本文降噪信号时域图与模拟仿真信号时域图相比可以看出，本文方法能够清晰看出信号的波形，真正实现降噪目的。在频域图中，小波变换降噪与模拟仿真信号频域图相比，同样不能提取出特征信号；而本文方法与小波变换降噪效果相比，能够非常有效地提取模拟仿真信号的特征峰值，且能准确分析出模拟仿真信号设定的特征频率。由于噪声杂乱无章，随着噪声信号能量的增大，一定程度上抵消了周期信号的能量，故在模拟仿真信号进行降噪后，其时域图与频域图里表现出的幅值则相应减小，再加上滤波处理，也在一定程度上减小了特征信号的幅值。

5 实测轴承故障信号分析

为进一步验证本文方法的有效性，采用旋转机械振动分析及故障诊断试验平台系统，采集滚动轴承外圈故障的振动信号。试验中采用轴承型号为N205EM，滚柱个数为13，滚柱直径为7.5 mm，滚道节径为38.5 mm，转速为867 r/min；采样频率为20 kHz，采样点数为32 768，计算得到轴承外圈特征频率为75.6 Hz，轴频为14.45 Hz。重复采集16组数据进行分析，所得故障信号时域图与频谱图、小波降噪信号时域图与频谱图、本方法降噪信号时域图与频谱图见图5～图7。

图5 故障信号时域图与频谱图

图6 小波降噪信号时域图与频谱图

图7 本方法降噪信号时域图与频谱图

分析图5～图7可知，本文方法降噪后信号的时域波形与实测轴承故障信号、小波降噪后信号的时域波形相比，其噪声能量明显减弱；从实测轴承故障信号、小波降噪的频谱图可发现，虽然都能在轴承外圈故障特征频率(75.6 Hz)及2倍频、3倍频处找出故障频率峰值，但仍不能完全确定是否存在有调制现象，而在本文方法降噪后的频谱图中不仅能够发现在轴承外圈故障特征频率(75.6 Hz)及2倍频、3倍频处存在较为清晰的频率峰值，而且还能确定在这些故障特征频率处不存在调制谱线，根据上述故障频率特征便能判断轴承外圈存在故障。

6 结论

本文利用离散余弦变换的能量聚集特性和线性特性及旋转设备振动信号的循环平稳性，提出了一种基于离散余弦变换的轴承故障诊断方法。通过文中模拟仿真和故障信号两个例子可见，本文方法滤波器的形状、幅值、位置等完全由采集信号自身确定。

通过对上述仿真信号和故障信号降噪效果分析，本文方法与小波降噪方法相比，具有良好的消噪效果，能很好地抑制信号中各频段的噪声分量，避免了一些小能量的平稳或循环平稳分量当作噪声消除的缺点，更能有效地提取轴承故障信号的时频特征，为轴承故障诊断提供技术支持，有望应用到相关领域中。