关于有限n-表示模的Gorenstein类

何东林，樊 亮

（陇南师范高等专科学校数信学院，甘肃 陇南 742500）

Gorenstein模类是相对同调代数的研究热点之一.Auslander等[1]介绍了双边Noether环上有限生成模的G-维数.Enochs等[2]给出了一般环上Gorenstein内射模和Gorenstein投射模的定义.随后，仍有许多学者先后对其进行了研究和推广.特别地，2008年毛立新和丁南庆[3]引入了关于有限表示模的Gorenstein模，即Gorenstein FP-内射模.2012年Gao等[4]进一步讨论了左凝聚环上Gorenstein FP-内射模的若干性质及其刻画.有限n-表示模（即FPn型模[5-6]）是有限表示模的一个重要推广.2017年Bravo等[7]介绍了关于有限n-表示模的内射模，即FPn-内射模，它是FP-内射模的一个推广，并给出左n-凝聚环的若干刻画.众所周知，在左凝聚环上，（F P，F I）是一个完全遗传余挠理论，其中F P和F I分别表示所有FP-投射模和FP-内射模组成的类.受此启发，本文引入关于有限n-表示模的投射模（即FPn-投射模）的概念，并证明左n-凝聚环R上（F PnP，F PnI）是一个完全遗传余挠理论，其中F PnP和F PnI分别表示所有限n-表示投射模和内射模组成的类.进而介绍Gorenstein FPn-内射模的定义，研究其性质和等价刻画.

文中的环R均指有单位元的结合环，模指酉左R-模.P和I分别表示所有投射模和内射模组成的类.设n是非负整数，称左R-模M是有限n-表示的[7]，如果存在正合列Fn→Fn－1→…→F1→F0→M→0，其中Fi（0≤i≤n）是有限生成自由模.用F Pn表示所有有限n-表示模组成的类，则模类F Pn关于扩张、单同态的余核及直和因子封闭且F P0⊇F P1⊇F P2⊇…⊇ F Pn⊇….称环 R 是左 n-凝聚环[7]，如果 F Pn⊆F Pn＋1.显然左1-凝聚环就是左凝聚环.在左n-凝聚环上，F Pn关于满同态的核封闭.称左R-模N是FPn-内射模[7]，如果对任意M∈F Pn，都有用F PnI表示所有FPn-内射模组成的类，则F P0I⊆F P1I⊆F P2I⊆…⊆F PnI⊆…且F PnI关于扩张、直积和正向极限封闭.

设x和y是左R-模类.称正合列（ε）在HomR（x，－）下正合，如果对任意X∈x有（ε）在HomR（X，－）下正合.记类似地可定义和⊥y.称对子（x，y）是余挠对[8]（也称余挠理论），如果进而，如果对任意左R-模M都存在正合列0→Y→X→M→0和 0→M→Y′→X′→0，其中 X，X′∈x 且 Y，Y′∈y，那么称余挠理论（x，y）是完全的，如果对任意 X∈x和 Y∈y都有，那么称余挠理论（x，y）是遗传的.余挠理论（x，y）是遗传的等价于模类y是内射可解的，即y包含所有内射模且关于扩张和单同态的余核封闭.其余未涉及的概念和记号参见文献[9-11].

1 FPn-投射模与余挠理论

2 Gorenstein FPn-内射模

下文均假设R为左n-凝聚环.

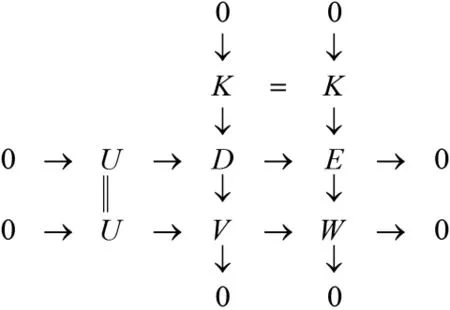
图1 V→W和E→W的拉回图

在正合列0→K→D→V→0中K∈GF PnI，由引理2.1得该序列在HomR（F PnP∩F PnI，－）下正合，且存在HomR（F PnP∩F PnI，－）下正合的正合列…→E1→E0→V→0，其中Ei∈F PnI.由上面两个正合列拼接可得正合列…→E1→E0→D→V→0，从而由引理2.1得V∈GF PnI.

引理2.3模类GF PnI关于扩张、单同态的余核及直和因子封闭.

证明先证对任意U∈GF PnI，都存在HomR（F PnP∩F PnI，－）下正合的正合列…→H1→H0→U→0，其中 Hi＝F PnP∩F PnI.由引理 2.2得存在正合列 0→K0→E0→U→0，其中E0∈F PnI且K0∈GF PnI.由定理1.2知（F PnP，F PnI）是一个完全遗传余挠理论.从而存在正合列0→L0→H0→E0→0，其中H0∈F PnP且L0∈F PnI.因为F PnI关于扩张封闭，所以H0∈F PnI，可见H0∈F PnP∩F PnI.构造拉回图如图2.由图2第一列和引理2.2知N0∈GF PnI.因为图2中间列和第三行正合列在HomR（F PnP∩F PnI，－）下正合，所以中间行正合列0→N0→H0→U→0在HomR（F PnP∩F PnI，－）下也正合.对N0重复上面对N的过程，如此继续，可得HomR（F PnP∩F PnI，－）下正合的正合列…→H1→H0→U→0，其中Hi∈F PnP∩F PnI.

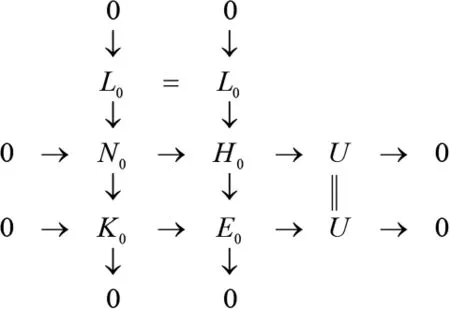
图 2 K0→E0 和H0→E0 的拉回图

设0→U→V→W→0是左R-模正合列.若U，W∈GF PnI，由上面的证明可知，存在HomR（F PnP∩F PnI，－）下正合的正合列

若U，V∈GF PnI，则存在HomR（F PnP∩F PnI，－）下正合的正合列0→K→E→V→0，其中E∈F PnI且K∈GF PnI.考虑拉回图，如图3.

图3 U→V和E→V的拉回图

由图3中第二列和第三行在HomR（F PnP∩F PnI，－）下正合，易得0→D→E→W→0在HomR（F PnP∩F PnI，－）下也正合.在正合列0→K→D→U→0中，K，U∈GF PnI且GF PnI关于扩张封闭，所以D∈GF PnI.从而存在HomR（F PnP∩F PnI，－）下正合的正合列（ξ）:…→H1→H0→D→0，其中 Hi∈F PnI且 D∈（F PnP ∩F PnI）⊥.将（ξ）和短正合列0→D→E→W→0拼接易得HomR（F PnP∩F PnI，－）下正合的正合列

…→H1→H0→E→W→0，

其中Hi∈F PnI且E∈F PnI.由D，E∈GF PnI及引理 2.1可得W∈（F PnP∩F PnI）⊥，进而W∈GF PnI.因此GF PnI关于单同态的余核封闭.

因为GF PnI关于扩张和直积封闭，根据文献[9]中命题1.4可得GF PnI关于直和因子封闭.

推论2.1完全F PnI-I分解X的每个核都是Gorenstein FPn-内射模.

引理2.4设0→U→V→W→0是左R-模正合列.若V，W∈GF PnI，则U∈GF PnI的充要条件是对任意H∈F PnP∩F PnI都有

证明（必要性）由引理2.1易证.

（充分性）设对任意H∈F PnP∩F PnI都有.由W∈GF PnI及引理2.3的证明过程知，存在HomR（F PnP∩F PnI，－）下正合的正合列0→K→H→W→0，其中K∈F PnI且H∈GF PnI.构造拉回图如图4.

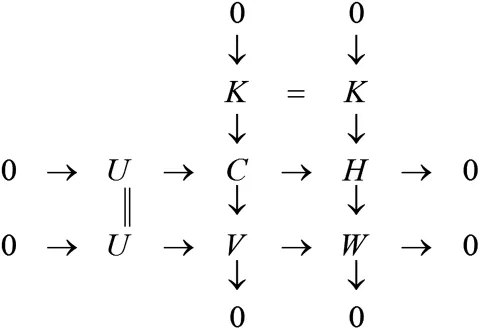
图4 V→W和U→W的拉回图

由图4中间列及GF PnI关于扩张封闭知C∈GF PnI.考虑中间行0→U→C→H→0，因为H∈F PnP∩F PnI且，所以该序列可裂.可见U是C的直和因子.又由引理2.3知GF PnI关于直和因子封闭，因此U∈GF PnI.

图 5 K0→C0 和E0→C0的拉回图

由图5中间列和第三行在HomR（F PnP∩F PnI，－）下正合得，中间行0→U0→E0→U→0在HomR（F PnP∩F PnI，－）下也正合.考虑拉回图如图6.

图 6 U0→K0 和C1→K0 的拉回图

…→E1→E0→U→0，其中 Ei∈F PnI.

根据引理2.1可得U是Gorenstein FPn-内射模.

3 结论

利用环模理论和同调代数的方法，研究了有限n-表示投射模和Gorenstein FPn-内射模的若干性质和等价刻画.结果表明在左n-凝聚环R上，（F PnP，F PnI）是一个完全遗传余挠理论，其中F PnP表示所有限n-表示投射模组成的类.从而补充了相对同调代数中关于余挠理论和有限表示模的相关理论.