基于分形插值的城市降雨时间序列精细化估算

孙欣跃

（辽宁省水资源管理集团有限责任公司，沈阳110003）

分形插值是基于分形基础理论的具体应用研究，能很好地描述生活中广泛存在的对象，往往具有复杂性和粗糙性。除此之外，分形插值函数灵活性强和稳定性高的特点使其广泛应用于水文地质、 动画仿真、图像处理等众多研究领域［1］。

1 研究区概况

济宁市山东省西南部的一个地级市， 济宁市气候四季分明，气温宜人。受热带海洋气团或热带海洋气团影响， 天气炎热多雨， 年平均降水量597～820mm；冬季多为偏北风，受极地大陆气团影响，多为晴冷天气；春秋两季为大气环流调整期，春季易干旱多风，变化迅速温暖；秋天凉爽，有时下雨。济宁市的水资源较为充沛，年降水量大，对于防洪减灾工作难度较大。

2 计算方法和数据

2.1 计算原理

分形插值是对具有分形特征的曲线进行的快速插值方法，其根据分形曲线的自相似性，基于迭代函数系统（IFS）实现。 首先要构造一个迭代函数系，以此来表示采用分形的插值，令吸引子A为插值函数的图形。对于{（xi，yi），i=0，1，···，N}∈R2，分形插值函数是 插 值 于{（xi，yi），i=0，1，···，N}的 一 个 连 续 函数f［x0，xn］→R，且其图形就是双曲迭代函数系统的吸引子A。

创建一个吸引子为插值函数f（x）的迭代函数系{R2：Wi，i=1，2···，N}，设函数系中的每个函数Wi是仿射变换，表示为［2］：

Wi∶R2→R2，i=1，2，…，N

2.2 降雨时间序列的提取

气象数据由中国气象信息中心官网下载， 数据类型为某气象站点气候资料的日值数据。 以数值形式的气象资料为每日平均资料， 时降雨资料可基于ArcMap于时刻降雨资料雨量图中提取， 逐小时雨量分布如图1。

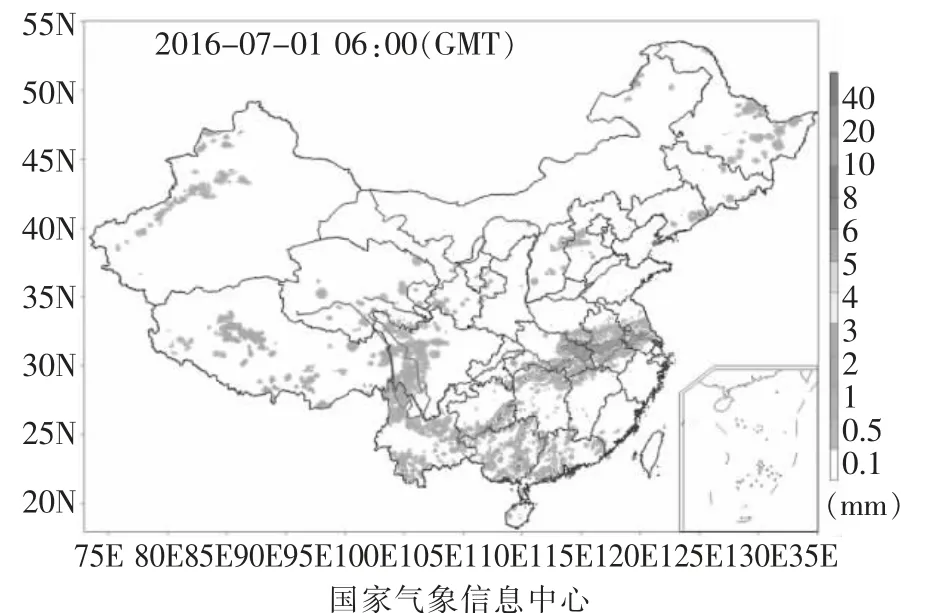
图1 逐小时雨量分布

每幅气象图代表某一小时的气象数据， 在某一具体气象站点多幅图的数据的提取就构成了该点某时间区间的序列。 本文采用的数据是小时时间间隔的降雨数据。 下载2018年6月30日12：00到2018年7月5日12：00时刻雨量图， 选取或创建指定气象站点（济宁为54326站点）的Shape 文件，提取该点（或多点）的时间序列数据。 其中点Shape数据为设定的气象数据提取位置。通过Spitial Analyst 中的提取分析工具，提取图像素数值，建立换算表，取图例中的中间值，得到的换算如表1。

表1 降雨数据提取对应

最终得到济宁市（气象站点58326）的120h连续降雨值，转换为降雨强度单位，降雨时间序列如图2。

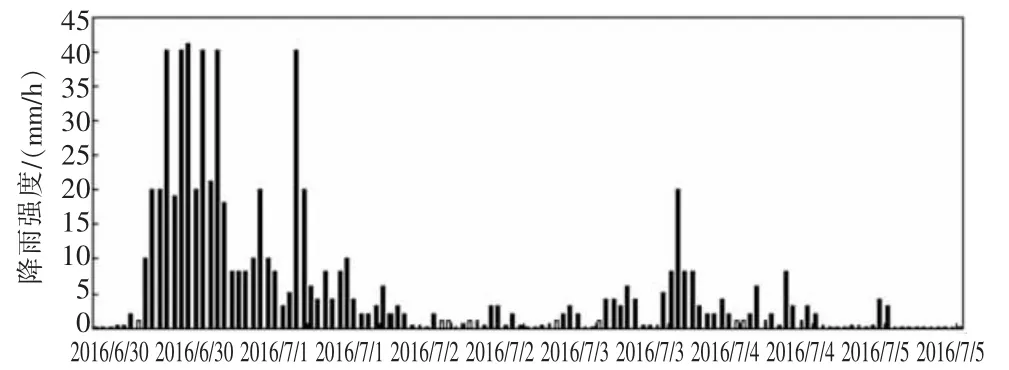
图2 120h降雨时间序列

3 研究结果

3.1 降雨数据分形特性分析

分形分析采取盒子覆盖法计算曲线的盒维数，通过绘制单位长度和覆盖所需的总正方形数量的双对数曲线得到［3］。选取若干不同尺度的r，一般情况下选取离散点时间序列样点周期的整数倍。 用边长为r的正方形对曲线进行覆盖，计算不同尺度r覆盖时间序列曲线所需单位正方形的总数N（r）。绘制ln N（r）-ln（1/r）的双对数散点图，采取最小二乘法估计拟合出散点斜率。 回归直线与散点的拟合就反应了降雨时间序列的自相似特性［4］。

根据分形维数的盒维数计算法， 采用MATLAB软件引入这些公式，改变小正方形的边长r，给定的单位长度r为两个时间单位（r=2），单位长度为r=2i/N（i=1，2，…，5），统计正方形数目N（r）。

表2 r覆盖统计

将表中的ln（1/ri）和ln（N（ri））数据值，添加趋势拟合线，可得到趋势拟合的回归直线。得到的回归方程为：y=1.012x+6.069。

图3 时间序列曲线盒覆盖双对数

根据分形盒维数的定义与原理， 得知该拟合直线的斜率D即为时间序列曲线的盒维数估计数值。所以维数为1.012。 双对数曲线的拟合相关系数R2为0.998。 从拟合直线的直观表象来看， 对数点分布在直线的附近，拟合相关率高达99.8%，说明此次降雨过程的时间序列曲线具有很强的局部与整体的相似性，定量反映了该时间序列曲线具有分形特性。

3.2 降雨时间序列的分形插值计算

由于对缺少实测降雨数据， 中国气象数据网站提供的地面逐小时降雨资料， 所以可依据时降雨时间序列的分形特性， 采用分形插值函数计算提取得到120个小时每两个时刻之间的降雨量。

对时刻进行排序，即构造120个插值点为p0（x0，y0）=（0，0.10）、p1（x1，y1）=（1，0.10）、p2（x2，y2）=（2，0.10）···p119（x119，y119）=（119，0.10）。 上述120个点是实现仿射分形插值函数构造的所需插值点，根据垂直比例因子非确定的取值方法，可初步得到各个仿射系数［5］。

以上计算过程可基于MATLAB软件程序文件实现，对已知初始点进行迭代，根据分形插值函数的计算规律，需要进行一次迭代过程，即在原两个数据点之间，插入118个数据点，可将原来以小时为单位的降雨时间序列细化到30s，得到插值后曲线，如图4。

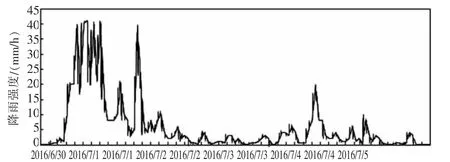
图4 分形插值后降雨时间序列

插值得到细化时间序列将插值分形曲线图与实测曲线图进行对比可看出，曲线走势相同，变化规律基本一致。 表3是插值数据和实测数据的平均值、方差和分形维数的比较。

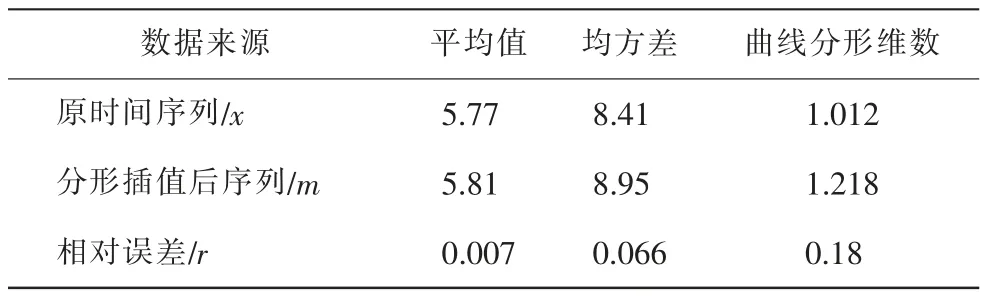
表3 原始数据与插值数据比较

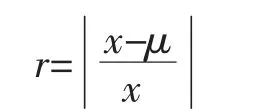
式中 m为插值数据；x为实测数据；r为相对误差。

3.3 分形插值与传统插值方法结果对比

与传统插值方法进行对比， 可看出分形插值在插值效果上具有明显优越性， 为120个数据线性插值的结果。 线性插值没有考虑已知连点间的具体变化过程，将两点直接用直线进行连接，而分形插值基于部分与整体的相似性， 将两点间变化的过程具体化，反映了局部特征。拉格朗日插值也属于一种常用的传统插值方法，又称为多项式插值。该插值方法的缺点在于插值节点个数的增加的同时， 不能确保两个插值节点之间插值函数一定能够很好地与被插值函数吻合。从理论角度来看，幂次数多项式需要的数据多，拟合结果比低幂次准确，但从舍入误差看，高次插值计算过程复杂，而且计算量较大，计算过程中会产生较大程度的误差累积。拟合过程中出现了“龙格现象”， 使得靠近区间端点处的拟合数值很大，曲线的变化速度较高，出现了较大误差。而分形插值法的误差值较小，所得结果较为精准如图5。

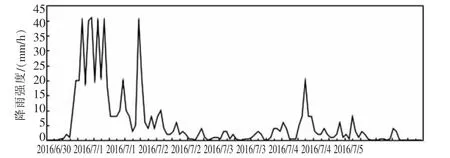
图5 线性插值后降雨时间序列

4 结语

本章从分形理论与分形的基本性质出发， 对济宁市2018年6月30日12：00 至2018年7月5日12：00连续120h的降雨时间序列进行了分形性分析， 得到该降雨时间序列曲线的分形盒维数为1.012，双对数曲线拟合度为99.8%，说明了该曲线具有很好的分形特性。进而应用分形插值理论，对该分形特性曲线运用迭代系统进行分形插值， 根据最终所需时间序列的精确度， 确定进行一次迭代， 实现每两个小时之间118 个插值点的生成， 最终将以小时为单位的时间序列细化处理为30s为单位的新时间序列。 将源数据与插值后数据进行误差统计，平均值、均方差和分形维数的误差分别为0.007，0.066，0.18，误差均在可接受范围内， 可满足当前中小型城市的城市雨洪建模的降雨数据需求。