自适应多滤波器的高效卷积算子目标跟踪算法

李国友，张凤煦，纪执安

自适应多滤波器的高效卷积算子目标跟踪算法

李国友，张凤煦*，纪执安

燕山大学工业计算机控制工程河北省重点实验室，河北 秦皇岛 066004

针对单一滤波器难以适应复杂变化的目标跟踪环境的问题，本文在高效卷积算子目标跟踪算法的基础上，提出了自适应多滤波器的目标跟踪算法。该算法使用时空正则化滤波器、一致性检验滤波器和高效卷积算子算法中的相关滤波器分别与目标特征进行卷积，得到三个滤波检测得分。其中，时空正则化滤波器是通过将时间正则化引入相关滤波损失函数而得到；一致性检验滤波器是通过反向定位前几帧目标，比较反向与正向定位坐标的误差，只有误差小于阈值时才更新滤波器；选择峰值旁瓣比最大滤波检测得分，估计目标的位置。使用OTB-2015数据集和UAV123数据集对改进算法进行测试，实验结果表明，本文算法能够更好地适应跟踪过程中的复杂变化的环境，具有较高的精度和鲁棒性。

目标跟踪；滤波器；时空正则化；一致性检验；高效卷积算子

1 引 言

目标跟踪广泛应用在视频监控、导弹制导、人机交互、人工智能、智能交通等领域，是计算机视觉研究中的重要分支[1-2]。目标跟踪是根据给定的目标位置和尺寸，在视频序列中估计出每一帧目标的位置和尺寸。目标追踪过程中存在着遮挡、光照变化、目标旋转、目标快速移动和背景杂乱等干扰因素，这些干扰因素影响目标跟踪精度[3]，从而难以实现对任意模型的跟踪。

目标跟踪算法主要可以分为生成式[4]和判别式[5]两种，生成式跟踪算法是在图像区域进行搜索，在图像区找出与目标外观模型最相似的区域作为目标，算法复杂度较大[6]。判别式跟踪算法将目标跟踪问题转化为二元分类问题，将目标从背景中分离出来，算法复杂度低，速度较快[7]。

近年来，相关滤波器引入到判别式跟踪算法的框架中，使目标跟踪的精度进一步提高。Bolme等[8]提出最小输出平方误差和相关滤波跟踪算法(minimum output sum of squared error, MOSSE)。Henriques等人[9]在CSK(circulant structure with kernels)算法中，使用循环矩阵结构在频域上做分析，将矩阵的运算转化为向量的点积，提高了运算速度。由于CSK使用的灰度特征受光照影响较大，Henriques等[10]提出采用梯度方向直方图特征(histogram of oriented gradient, HOG)的KCF算法，提高了滤波器对目标的跟踪效果。Danelljan 等[11]针对KCF算法中的边界效应问题，在SRDCF (spatially regularized discriminative correlation filters)算法中在空间域上对滤波器进行正则化，有效地抑制了背景区域的响应。之后在连续卷积算子算法(continuous convolution operators for tracking，C-COT)[12]中使用隐式插值模型，将DCF(discriminative correlation filters)[13]中的单分辨率特征映射转换为连续空间域的多分辨率特征映射，使跟踪精度进一步提高。Danelljan等[14]提出的高效卷积算子目标跟踪算法(efficient convolution operators，ECO)，在特征提取上对连续卷积算子算法进行了简化，降低了算法计算复杂度，并使用高斯混合模型简化了训练集，优化了模型更新策略。Li等[15]将时间正则化引入SRDCF算法[11]中，改善了遮挡和大幅形变情况下滤波器过度更新的情况。

尽管目前的目标跟踪算法取得了很好的跟踪效果，但是现存的跟踪算法主要使用单个滤波器对目标进行跟踪。在实际目标跟踪过程中，目标的姿态各异，所处的环境复杂多变，单一滤波器难以应对视频序列的复杂变化。当目标发生巨大形变或遮挡时，如果单一滤波器过度更新，将会造成滤波器对新样本的过拟合；如果单一的滤波器积累了过多的噪声信息，将会难以准确地确定目标位置，使跟踪精度下降。随着深度特征引入目标追踪领域[16]，滤波器对目标的识别能力有所增强，但运算量过大，算法实时性不高。

针对单一滤波器难以适应目标跟踪过程中复杂变化的环境的问题，本文采用多个滤波器对目标进行跟踪[17]。根据视频序列相邻帧变化不会很大的原理，引入时间正则化[15]，训练时空正则化滤波器。对于追踪过程中出现的遮挡等各种噪声问题，引入一致性检验对序列目标进行反向定位，根据前后定位误差的大小，对滤波器进行选择性更新，得到一致性检验滤波器。然后利用时空正则化滤波器、一致性检验滤波器和ECO算法中的相关滤波器分别对目标特征进行卷积，得到三个滤波检测得分。最后根据三个滤波器滤波检测得分的峰值旁瓣比(peak-to-side ratio, PSR)的大小，选择最佳滤波检测得分确定的目标位置。采用OTB-2015数据集[18]和UAV123数据集[19]评估本文算法的性能，实验结果表明，改进的算法具有更高的精度和鲁棒性。

2 ECO跟踪算法

ECO算法[14]提出了因式分解卷积操作，减少模型中参数的维数，并且使用高斯混合模型(GMM)来生成不同的模型组件，将相似的模型归为一类，防止了目标出现过拟合，同时降低模型更新频率，提高了运算效率，避免了模型的漂移问题。

2.1 分解卷积算子

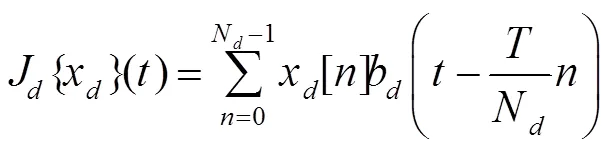
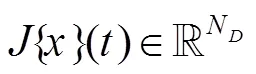
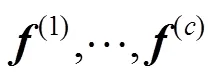
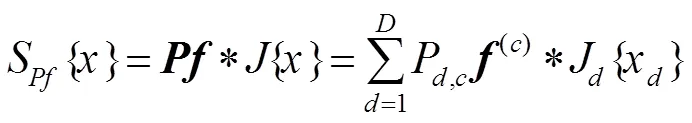
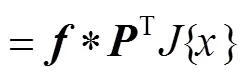
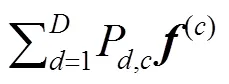
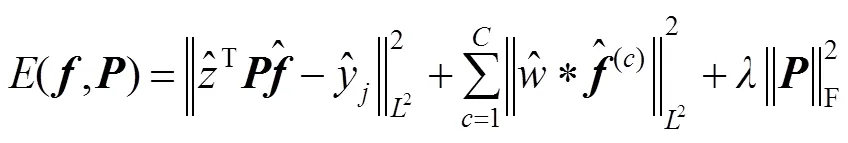
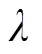
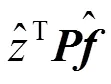
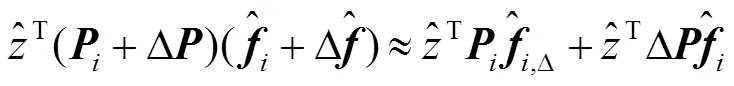
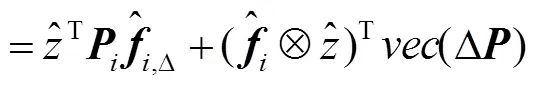
将一阶近似式(4)代入式(3)中，得到第次迭代处的高斯-牛顿子问题：

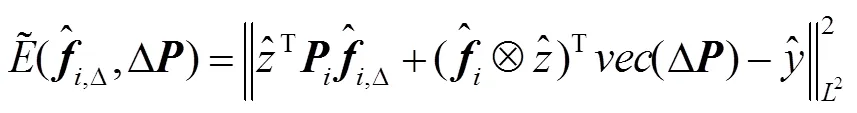
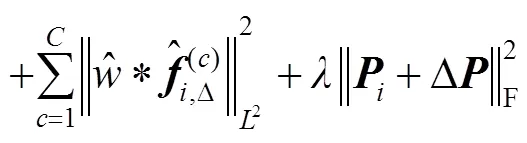
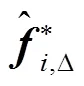
2.2 生成样本空间模型

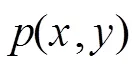
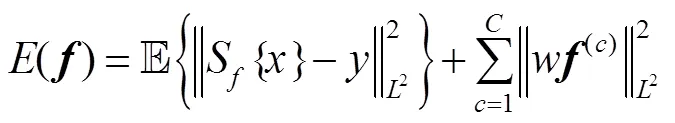
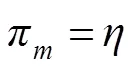
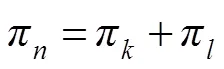
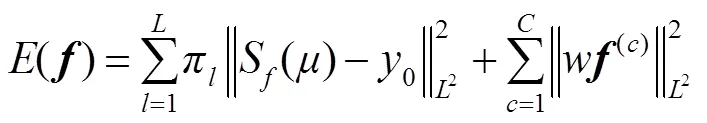
利用样本空间模型，将样本数量从减少到=/8，提高了运算效率和跟踪性能。

2.3 ECO算法基本流程

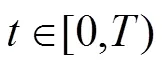
最后使用牛顿法对滤波响应得分函数进行优化，得到目标的估计位置，并进行下一帧目标的跟踪。每隔s帧使用共轭梯度法对滤波器进行更新，投影矩阵在以后每一帧中保持不变。ECO算法的初始化及具体流程如图1所示。

3 自适应多滤波器算法

本文训练时空正则化滤波器、一致性检验滤波器和ECO算法中的相关滤波器。其中，时空正则化滤波器能够很好地适应目标外观的巨大变化，一致性检验滤波器能够防止滤波器更新过程中引入过多的噪声信息，而ECO算法中的相关滤波器包含了最全面的目标特征信息。当目标发生大幅形变时，时空正则化滤波器具有较好的跟踪效果；当目标及背景杂乱噪声较多时，一致性检验滤波器具有较高的鲁棒性；当跟踪环境相对平稳，干扰较少时，ECO算法中的相关滤波器能够准确地确定目标位置。

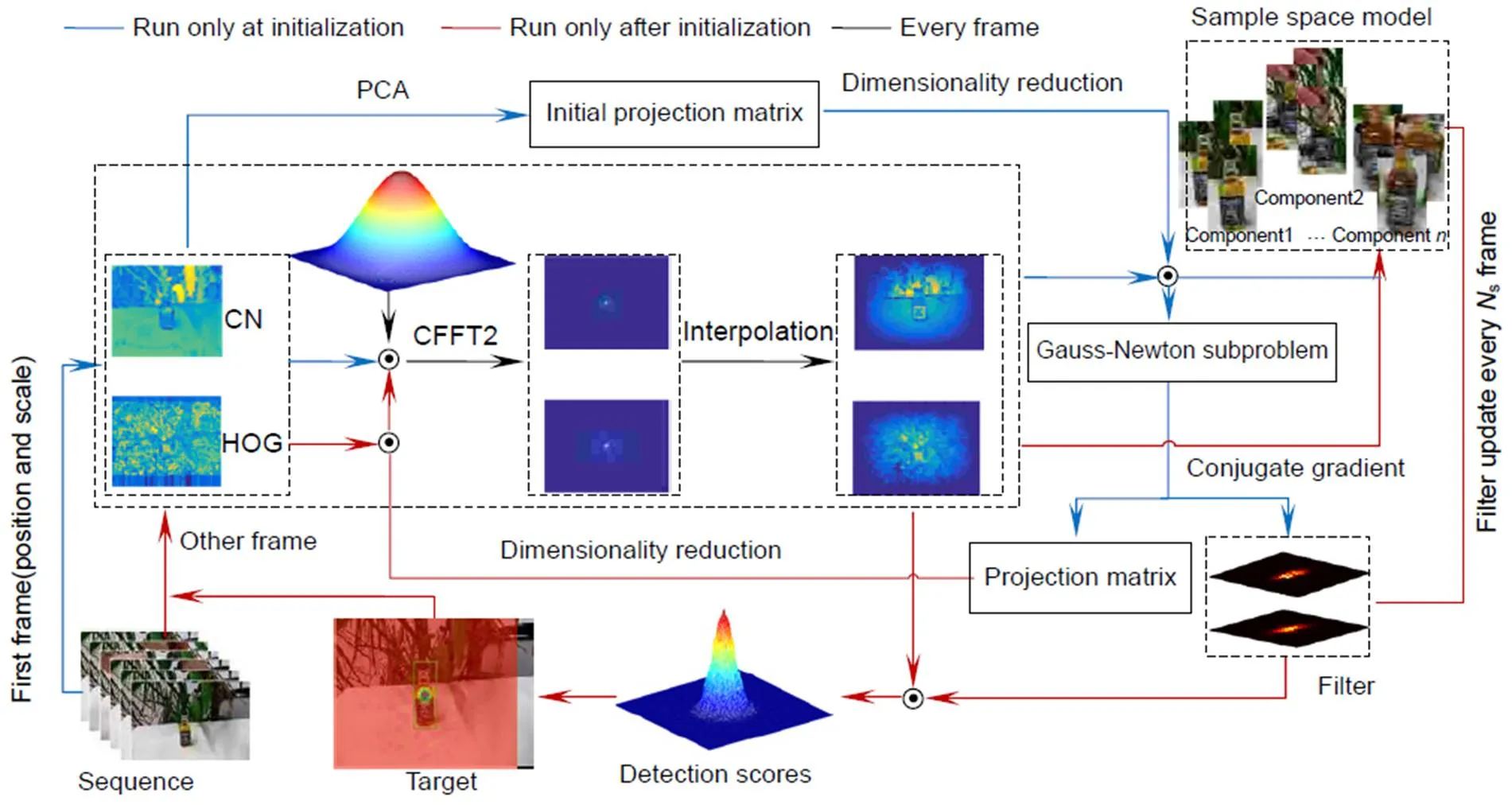
图1 ECO算法流程图

3.1 时空正则化滤波器

当出现一个新的样本实例时，首先对目标搜索区域进行特征提取，得出样本的标签，然后根据新实例标签更新滤波器。一般情况连续相邻帧的目标变化不大，新的滤波器与之前的滤波器具有一定的相似性，同时新的滤波器也需要尽可能多地体现出新样本的特征，以保证能够正确地识别新目标。STRCF (spatial-temporal regularized correlation filters)算法[15]中的损失函数加入了时间正则化，防止了滤波器对新样本的过拟合，在目标遮挡和大幅形变情况下准确率和鲁棒性都表现良好。在不同环境中自适应地调整滤波器，能够更好地适应目标跟踪过程中的各种环境。

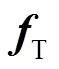
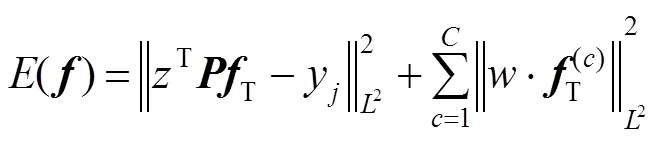
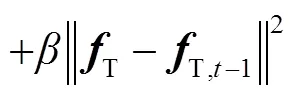
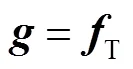
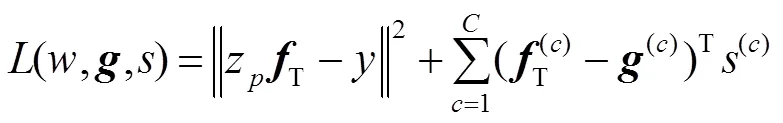
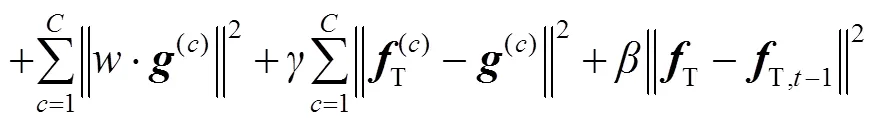
式中：为拉格朗日乘数，为惩罚因子，引入辅助变量=/，则可化简为

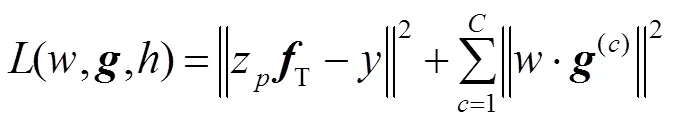
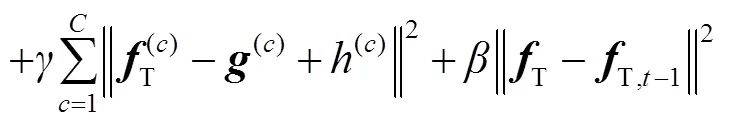
因此损失函数的最优解可以转化为采用交替方向乘子算法交替求解以下子问题：

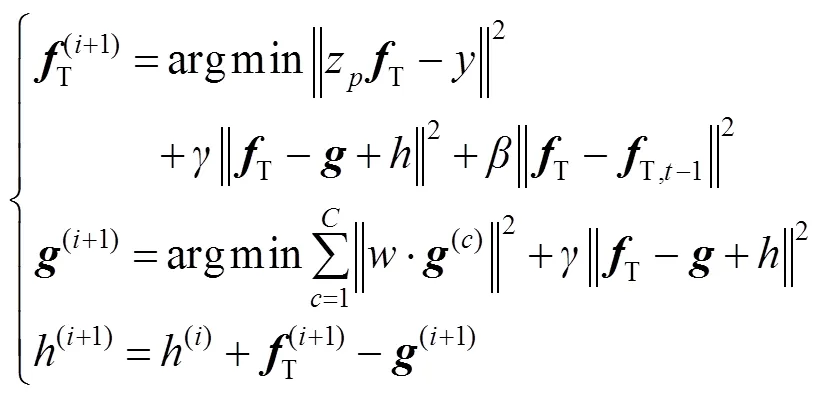
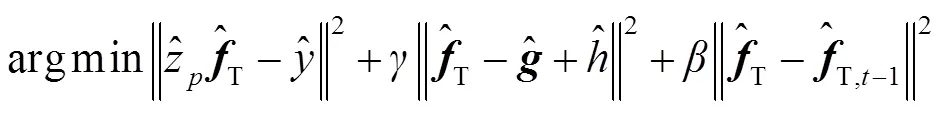
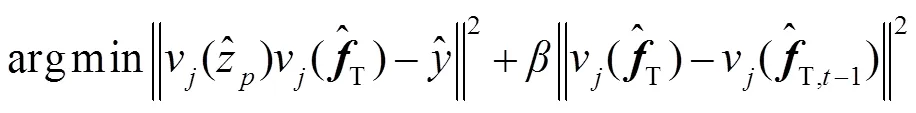
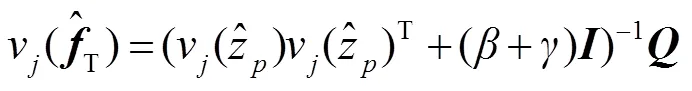
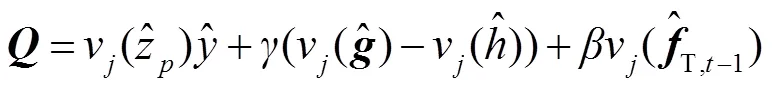
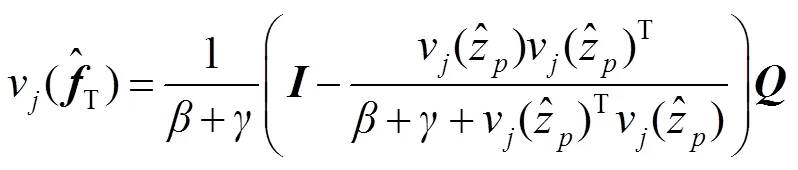
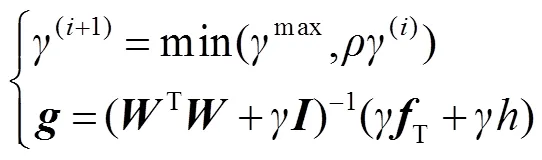
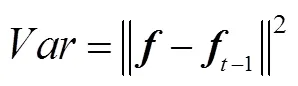
3.2 一致性检验滤波器模型

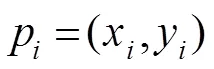
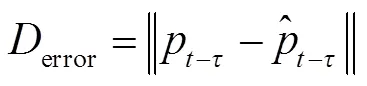
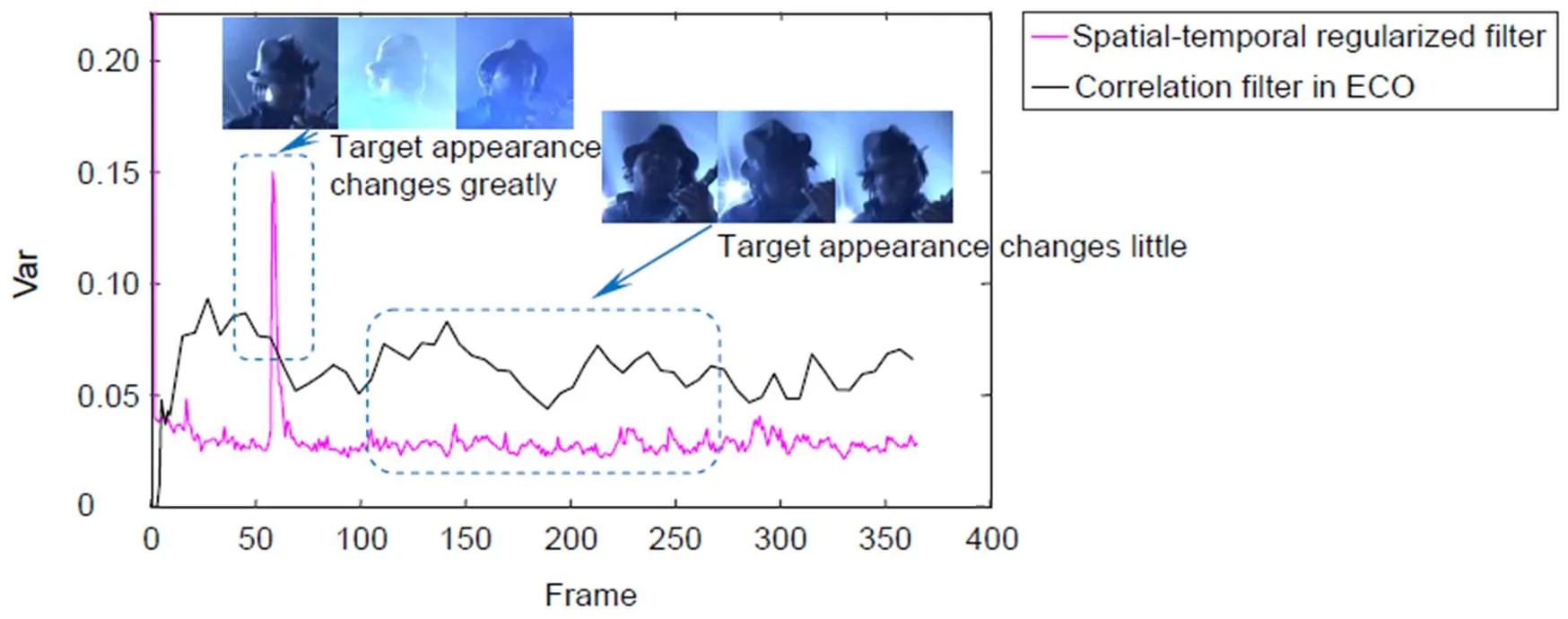
图2 时空正则化滤波器的随帧变化

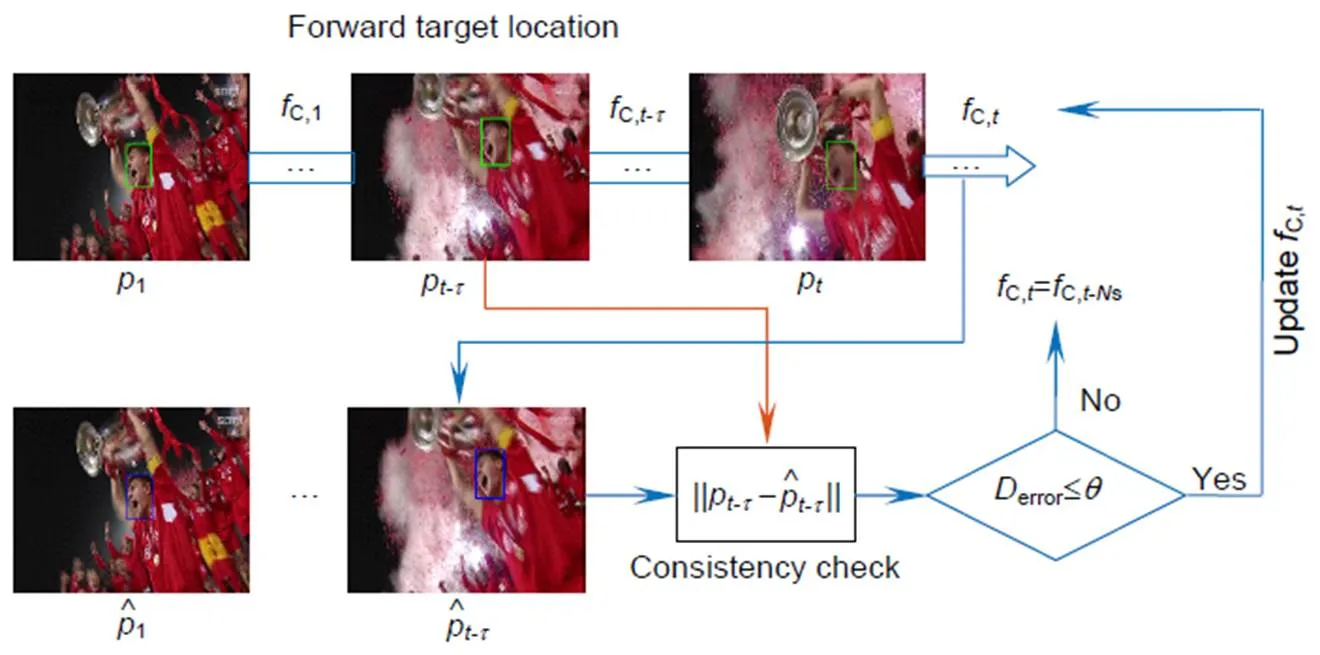
图3 一致性检验滤波器训练流程

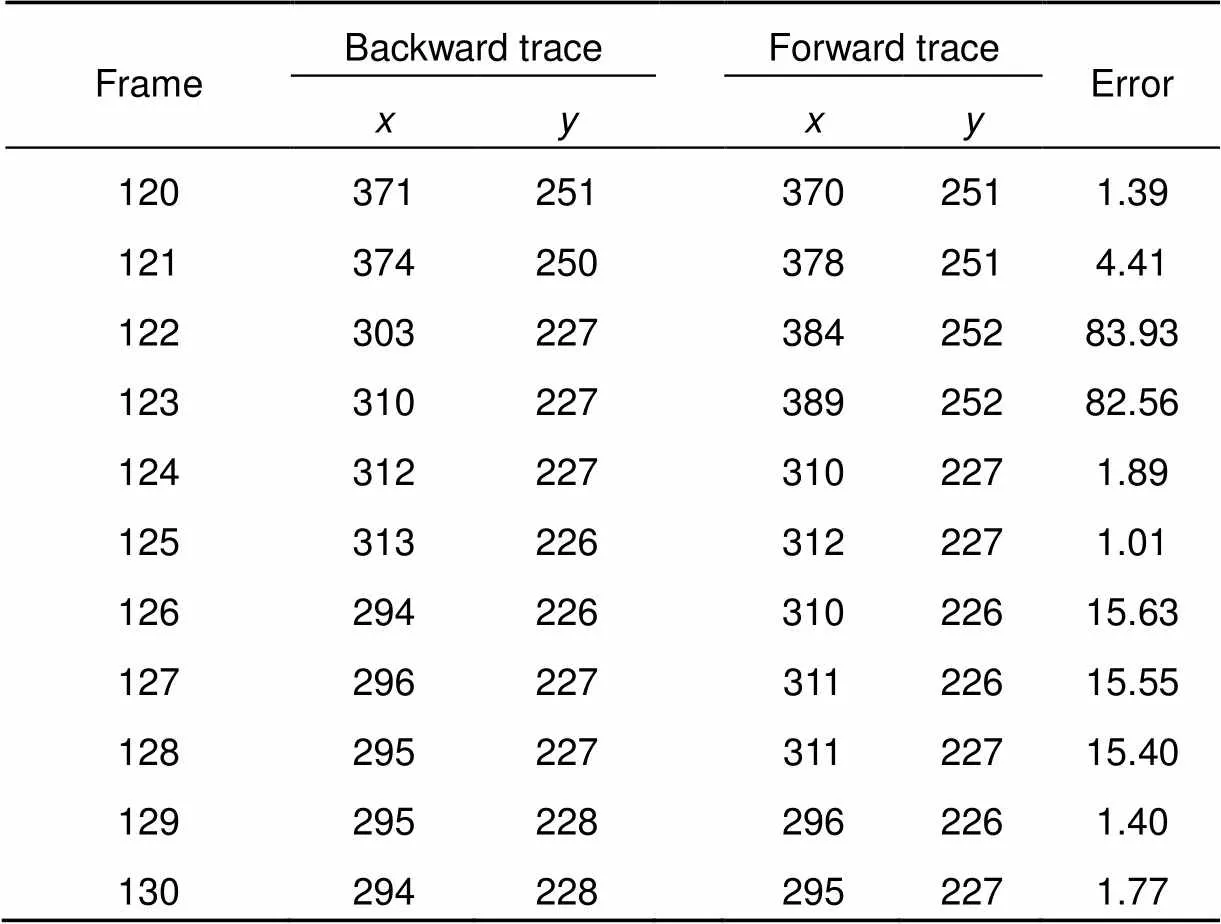
表1 前向与后向目标轨迹坐标

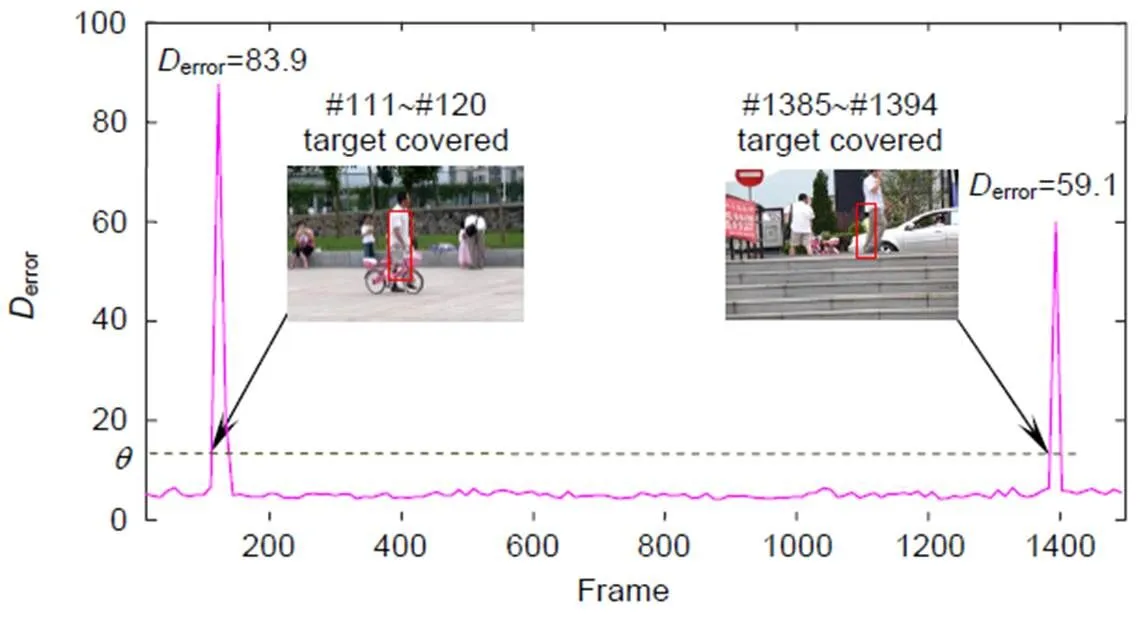
图4 前后向距离误差

3.3 最优滤波器模型选择

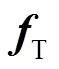
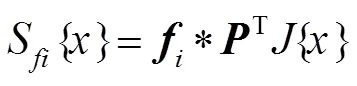
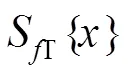
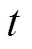
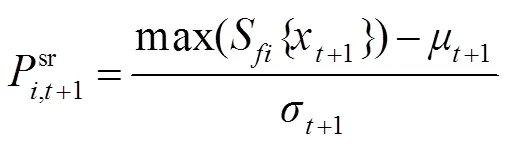
图5展示了目标跟踪精度与峰旁比的关系，其中图5(a)为ECO算法在OTB-2015数据集中的平均中心位置误差(center location error，CLE)与平均峰旁比的二次拟合曲线。可以看出当峰旁比的值越大时，中心像素误差越小，目标跟踪的精度越高。图5(b)为部分帧的滤波检测得分、峰旁比和跟踪结果。可见峰旁比的值越大，目标估计位置越接近真实位置。

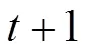
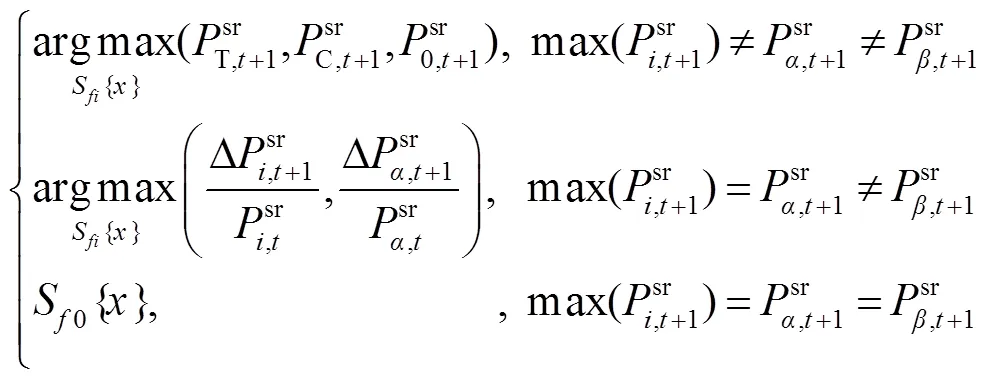
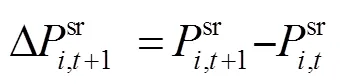
图6为Skating2序列在跟踪过程中不同滤波检测得分的峰旁比。可以看出在整个序列中三个滤波检测得分的峰旁比是不断变化的。当目标外观多变时，时空正则化滤波器的检测得分峰旁比较高，当目标出现遮挡或多噪声时，一致性检验滤波器的检测得分峰旁比较高。因此使用峰旁比较高的滤波波检测得分估计目标位置。

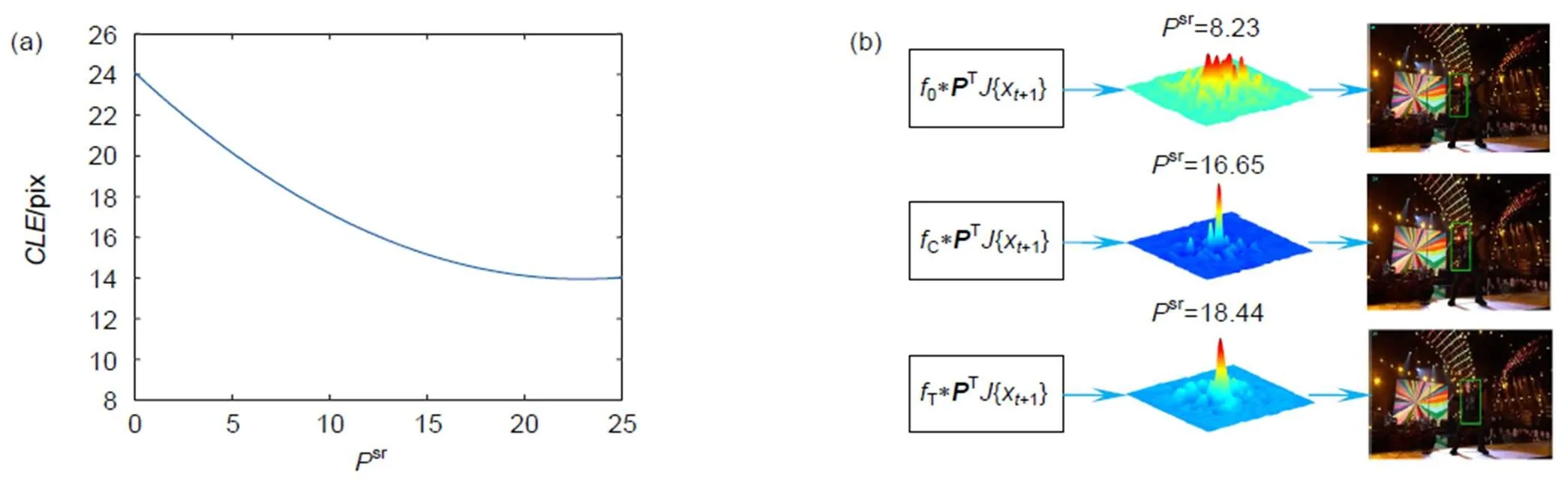
图5 目标跟踪精度与峰旁比的关系。(a) 峰旁比与跟踪精度关系曲线；(b) 部分帧的滤波检测得分、峰旁比和跟踪结果

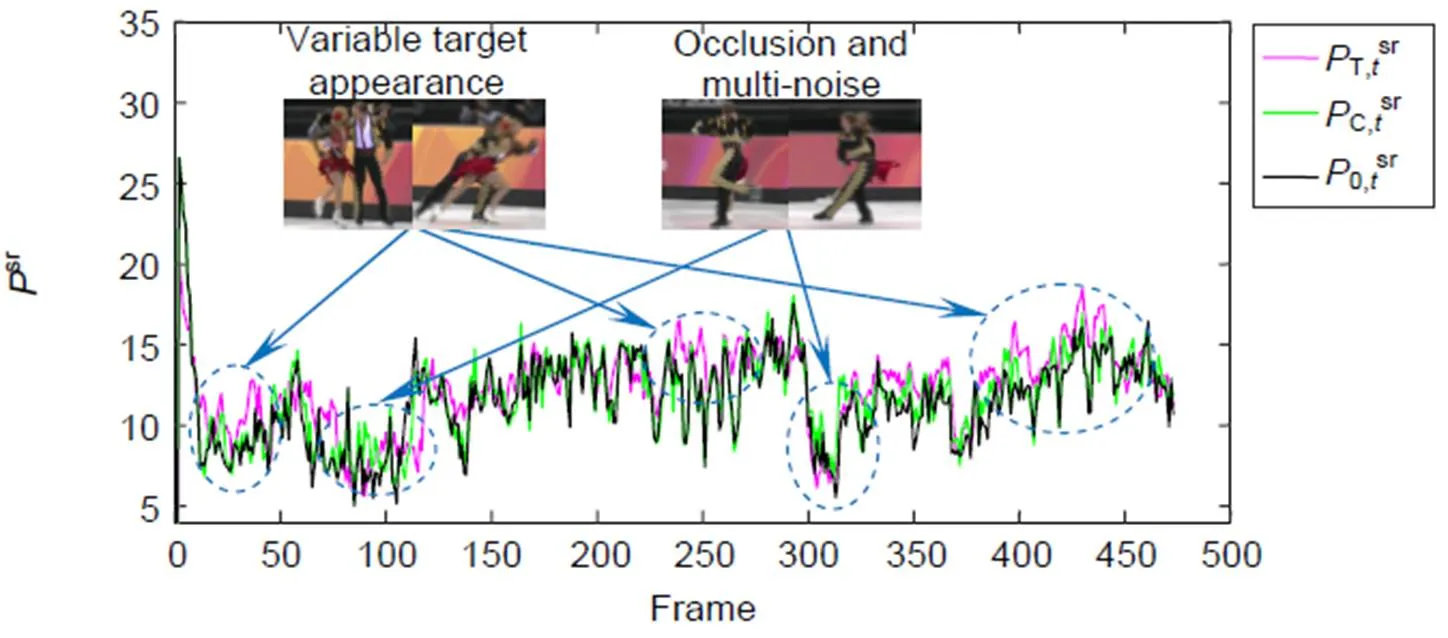
图6 不同滤波检测得分峰旁比

在本文算法中，利用时空正则化滤波器、一致性检验滤波器和ECO算法中的相关滤波器同时对目标特征进行卷积，得到三个滤波检测得分。利用式(22)的多滤波器决策模型，选择最优的滤波检测得分。根据最优的滤波检测得分，估计目标的所在位置。自适应多滤波器的目标跟踪算法具体流程如图7所示。

4 实验结果与分析

4.1 实验环境与方法

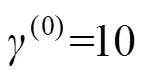
对于本文实验结果，采用中心位置误差(CLE，用CLE表示)和重叠率(overlapping ratio，OR，用OR表示)两种方法进行评价：

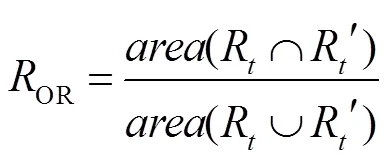
在OTB-2015中的得出精确度图(precision plot)和成功率图(success plot)两种评价标准。精确度是指跟踪目标中心位置和目标真实位置的误差小于20 pixel的跟踪序列所占的百分比；成功率为跟踪目标与真实目标的重叠率大于阈值0.5的帧数占跟踪序列中所有帧数的百分比。

本实验使用一次通过评估方法(one-pass evaluation, OPE)的精确度图和成功率图评估改进后算法的性能。在OTB-2015数据集[25]中自带的算法和ECO[19]、fDSST(fast discriminative scale space tracker)[27]、KCF[15]、STRCF[20]、HCF (Hierarchical convolutional features)[28]、MEEN (multiple experts using entropy minimization)[29]、Staple(sum of template and pixel-wise lear-ners)[30]、LCT(long-term correlation tracking)[31]等主流的跟踪算法进行性能比较，在UAV123数据集[26]上采用ECO[19]、DSST、fDSST[27]、KCF[15]、STRCF[20]、HCF[28]、Staple[30]、LCT[31]、LEDS (large-displacement tracking vis estimation of similarity)[32]与本文算法作对比。在精度图和成功率图上只显示排名靠前的10种跟踪算法的结果，以便于观察。

4.2 定量分析

图8是排名前10种算法在OTB-2015序列集上的总精确度图和成功率图，改进的算法的精确度为88.3%，比ECO算法提高了4.7%。改进的算法成功率为79.1%，比原始的ECO算法提高了2.8%。改进的算法精度和成功率均排名第一。

图7 多滤波器目标跟踪算法流程图

Fig. 7 Multi-filter target tracking algorithm flow chart

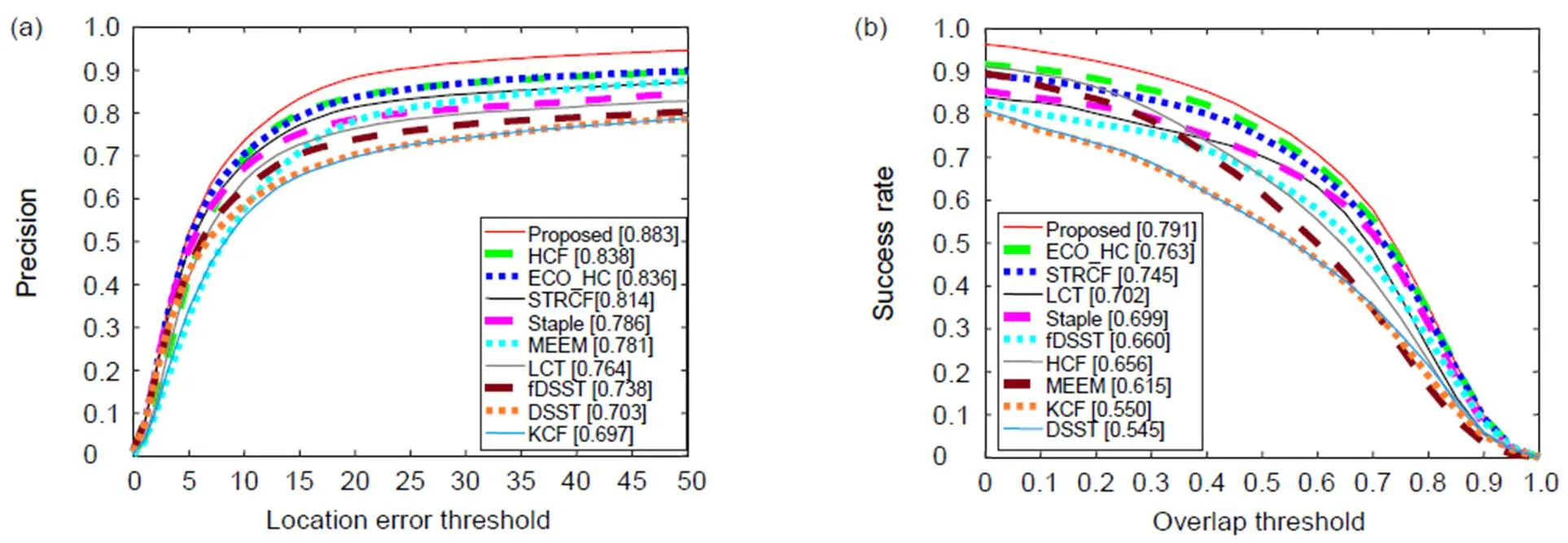
图8 OTB2015 评估OPE 精确度图和成功率图

在OTB-2015数据集中的测试视频的跟踪难点主要包括：光照变化(IV)、尺度变化(SV)、平面内旋转(IPR)、平面外旋转(OPR)、遮挡(OCC)、形变(DEF)、运动模糊(MB)、快速运动(FM)、相似背景干扰(BC)、出视野(OV)、低分辨率(LR)等。为了验证改进算法在各种跟踪难点下的鲁棒性，在这11种不同的跟踪情况下，得出改进后的算法和5种对比算法的精度和成功率如表2和表3所示。

由表2可以看出，改进的算法在11种不同跟踪情况下，有9种情况精度排名为第一，只有在低分辨率和快速移动情况下精度排名第二，且比原始的ECO算法有所提高。表3中的不同算法的成功率可知，本文改进的算法在不同跟踪情况下的成功率均排名较高，且有9种情况下排名第一。因此改进的算法具有较高的精度和鲁棒性，能够很好地应对复杂场景和目标多变的情况下的目标跟踪问题。

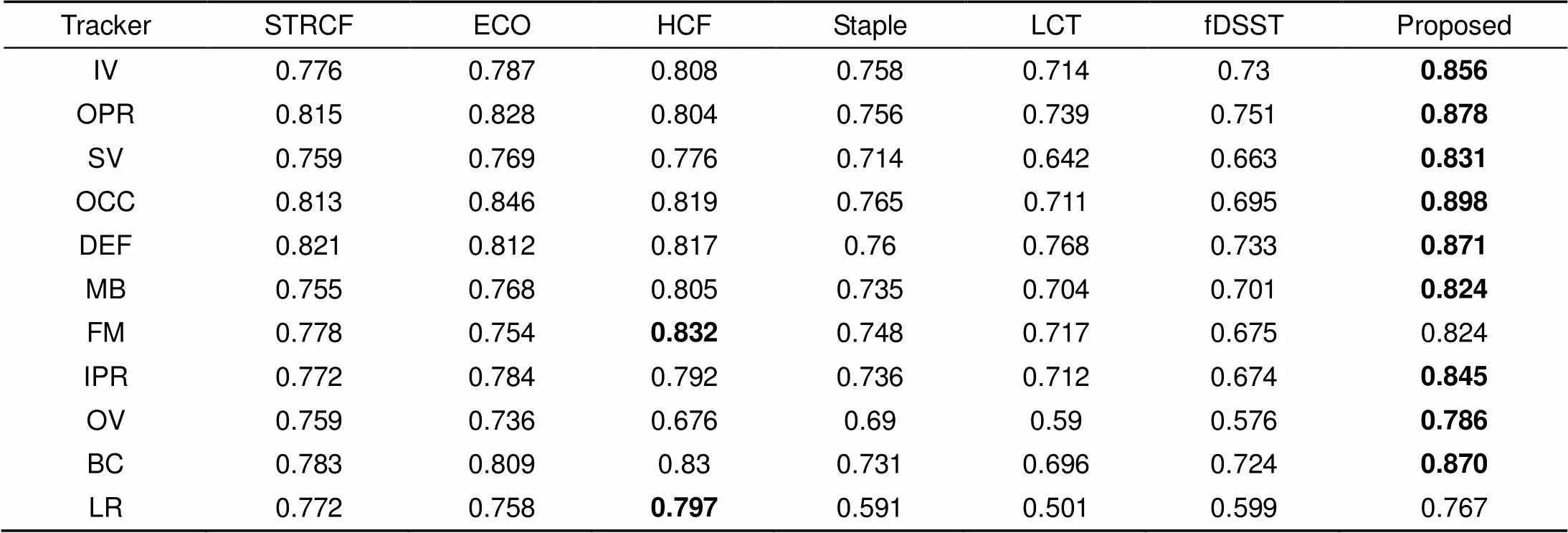
表2 不同情况下跟踪算法的精度

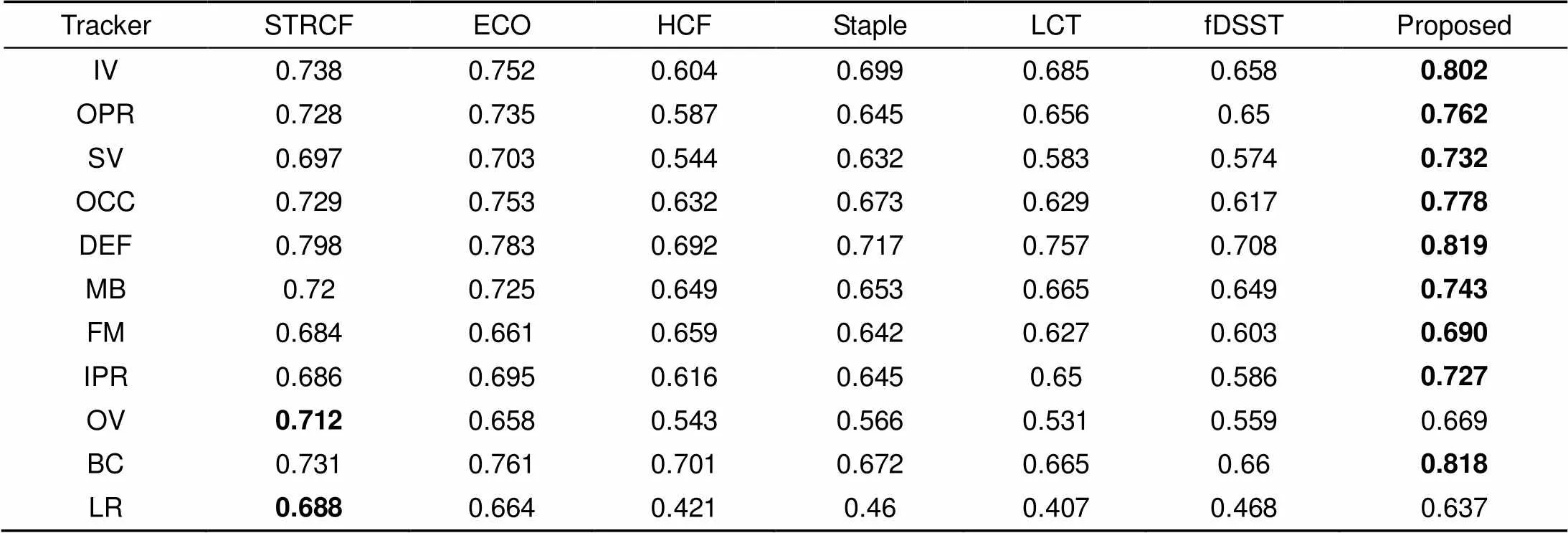
表3 不同情况下跟踪算法的成功率

表4为本文算法与精度和成功率排名靠前的8种算法的平均重叠率、中心位置误差和速度比较结果。改进的算法与原ECO 算法相比较，平均重叠率提高了3%，中心位置误差提高了9 pixels。改进的算法在OTB-2015数据集上的平均速度为 30.5 f/s，能够满足算法实时性要求。因此，本文采用的多滤波器跟踪算法，能够更好地适应目标跟踪过程中的复杂变化，提高了跟踪的准确性，使算法具有更高的鲁棒性。

为进一步验证改进算法的准确性，本文在UAV123数据集上继续对改进算法的精度和成功率进行评估，如图9所示。通过对比试验，本文改进的算法在精度和成功率上均排名第一。相比ECO算法，精度和成功率均有所提高。

4.3 定性分析

在OTB-2015数据集中选取的具有代表性的视频序列的跟踪数据，如图10所示。其中包含光照变化、运动模糊、尺度变化、快速移动、相似目标干扰等各种复杂变化。本节使用ECO、MEEM、STRCF、HCF、Staple、fDSST等精度较高算法在不同场景中跟踪过程中定性地对比分析目标跟踪算法的精确性和鲁棒性。

Twinnings序列中，要跟踪的目标是手里的书。在149帧目标由近变远，尺度发生变化，MEEN、HCF的算法没有很好地适应目标尺度变化。在第240帧，目标因发生旋转导致外观巨大变化，到331帧后，当目标再次发生尺度变化时，ECO算法的尺度和位置发生偏移。Biker序列中在63帧~94帧时目标快速移到另一条轨道，此时发生运动模糊、快速移动等干扰因素，在目标发生转向时，STRCF算法发生漂移。到第94帧目标完全跳向右边轨道后，只有本文算法和ECO算法定位到目标位置，且本文算法的精度最高。因此，本文算法能够在目标外观发生巨大形变和运动模糊的情况下准确地跟踪目标。

在Skating2-2序列中，目标是双人滑冰中的男性，序列中存在目标快速移动和相似目标干扰等问题。第13帧时，ECO算法发生短暂漂移，由于50帧前时目标发生遮挡除本文算法外的其它算法精度有所下降，经过目标的多次遮挡和旋转，到第454帧，只有本文算法准确定位到目标位置。因此本文算法能够在快速移动和相似目标干扰情况下保持较高的精度。

表4 8种算法平均重叠率、中心位置误差和速度

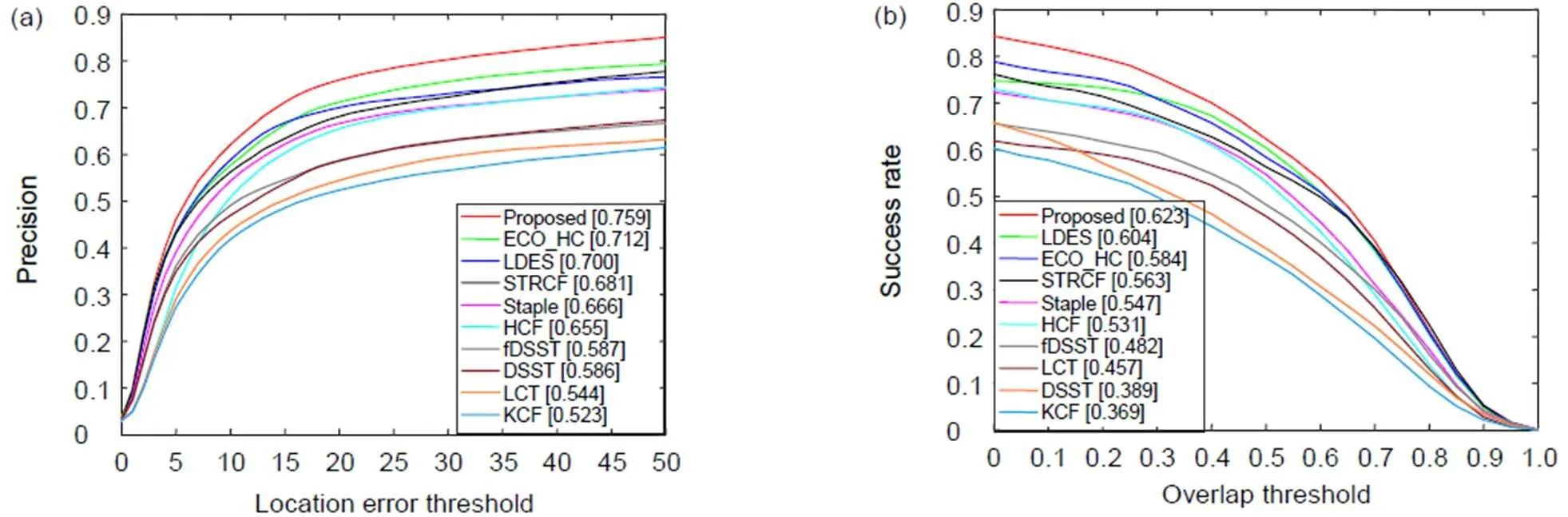
图9 UAV123评估OPE精确度图和成功率图

图10 数据集上部分测试视频上的跟踪结果

Shaking序列中的目标手拿小提琴的乐队成员的脸存在严重的光照变化。在第10帧7种算法都能定位目标位置；由于灯光干扰和目标的移动，到21帧Staple和HCF发生漂移；到216帧，Staple定位到其它相似目标位置，ECO和STRCF尺度准确性下降，本文算法精确定位目标位置。Bolt序列中的目标是在跑道上比赛的右数第四个运动员，其中存在多个相似目标。第100帧Staple算法的尺度估计精度下降，到239帧由于目标的快速移动，追踪精度均有所下降，本文算法能够保持高精度定位目标位置。因此，改进算法在相似目标干扰和目标快速移动情况下具有较强的鲁棒性。

5 结 论

本文在高效卷积算子目标跟踪算法的框架上，针对单一滤波器难以适应各种环境下目标跟踪的问题，提出自适应多滤波器的目标跟踪算法。本文训练了时空正则化滤波器、一致性检验滤波器和ECO算法中的相关滤波器。其中，时空正则化滤波器改善了滤波器过度更新的情况，一致性检验滤波器减少了在滤波器更新过程中引入的噪声信息，ECO算法中的相关滤波器保留了最全面的目标及背景特征信息。使用三个滤波器同时对目标特征进行卷积，得到三个滤波检测得分。对不同滤波器的滤波检测得分的峰旁比进行比较，选择出最佳的滤波检测得分。根据最佳的滤波检测得分，估计目标的位置。本文在OTB-2015和UAV123数据集上评估改进算法的性能，通过定性和定量的分析，本文算法在复杂环境下的跟踪精度和成功率相对于传统ECO算法均有所提高。因此改进的算法能更好地适应目标追踪过程中环境的复杂变化，具有较高的精度和鲁棒性。

[1] Lu H C, Li P X, Wang D. Visual object tracking: a survey[J]., 2018, 31(1): 61–76.卢湖川, 李佩霞, 王栋. 目标跟踪算法综述[J]. 模式识别与人工智能, 2018, 31(1): 61–76.

[2] Fan X S, Xu Z Y, Zhang J L. Dim small target tracking based on improved particle filter[J]., 2018, 45(8): 170569.

樊香所, 徐智勇, 张建林. 改进粒子滤波的弱小目标跟踪[J]. 光电工程, 2018, 45(8): 170569.

[3] Li S S, Zhao G P, Wang J Y. Distractor-aware object tracking based on multi-feature fusion and scale-adaption[J]., 2017, 37(5): 0515005.

李双双, 赵高鹏, 王建宇. 基于特征融合和尺度自适应的干扰感知目标跟踪[J]. 光学学报, 2017, 37(5): 0515005.

[4] Ross D A, Lim J, Lin R S,. Incremental learning for robust visual tracking[J]., 2008, 77(1–3): 125–141.

[5] Babenko B, Yang M H, Belongie S. Robust object tracking with online multiple instance learning[J]., 2011, 33(8): 1619–1632.

[6] Zhu W Q, Liu Y, Bian L,. Survey on object tracking method base on generative model[J]., 2017, 38(1): 41–47.

朱文青, 刘艳, 卞乐, 等. 基于生成式模型的目标跟踪方法综述[J]. 微处理机, 2017, 38(1): 41–47.

[7] Ge B Y, Zuo X Z, Hu Y J. Review of visual object tracking technology[J]., 2018, 23(8): 1091–1107.

葛宝义, 左宪章, 胡永江. 视觉目标跟踪方法研究综述[J]. 中国图象图形学报, 2018, 23(8): 1091–1107.

[8] Bolme D S, Beveridge J R, Draper B A,. Visual object tracking using adaptive correlation filters[C]//, San Francisco, CA, USA, 2010.

[9] Henriques J F, Caseiro R, Martins P,. Exploiting the circulant structure of tracking-by-detection with kernels[C]//, Berlin, Heidelberg, 2012: 702–715.

[10] Henriques J F, Caseiro R, Martins P,. High-speed tracking with kernelized correlation filters[J]., 2015, 37(3): 583–596.

[11] Danelljan M, Häger G, Khan F S,. Learning spatially regularized correlation filters for visual tracking[C]//, Santiago, Chile, 2015: 4310–4318.

[12] Danelljan M, Robinson A, Khan F S,. Beyond correlation filters: learning continuous convolution operators for visual tracking[C]//, Cham, 2016: 472–488.

[13] Lukežic A, Vojír T, Zajc L C,. Discriminative correlation filter with channel and spatial reliability[C]//, Honolulu, HI, USA, 2017: 4847–4856.

[14] Danelljan M, Bhat G, Khan F S,. ECO: Efficient convolution operators for tracking[C]//, Honolulu, HI, USA, 2017: 6638–6646.

[15] Li F, Tian C, Zuo W M,. Learning spatial-temporal regularized correlation filters for visual tracking[C]//, Salt Lake City, UT, USA, 2018: 4904–4913.

[16] Hu S, Shao Y M, Sun X. Review of object tracking based on convolutional neural networks[J]., 2018, 28(3): 207–213.

胡硕, 赵银妹, 孙翔. 基于卷积神经网络的目标跟踪算法综述[J]. 高技术通讯, 2018, 28(3): 207–213.

[17] Sun H, Li J, Du B,. Correlation filtering target tracking based on online multi-lifespan learning[J]., 2017, 45(10): 2337–2342.

孙航, 李晶, 杜博, 等. 基于多阶段学习的相关滤波目标跟踪[J]. 电子学报, 2017, 45(10): 2337–2342.

[18] Wu Y, Lim J, Yang M H. Object tracking benchmark[J]., 2015, 37(9): 1834–1848.

[19] Mueller M, Smith N, Ghanem B. A benchmark and simulator for UAV tracking[C]//, Cham, 2016: 445–461.

[20] Danelljan M, Häger G, Khan F S,. Discriminative scale space tracking[J]., 2017, 39(8): 1561–1575.

[21] Ma C, Huang J B, Yang X K,. Hierarchical convolutional features for visual tracking[C]//, Santiago, Chile, 2015: 3074–3082.

[22] Zhang J M, Ma S G, Sclaroff S. MEEM: robust tracking via multiple experts using entropy minimization[C]//, Berlin, 2014: 188–203.

[23] Bertinetto L, Valmadre J, Golodetz S,. Staple: Complementary learners for real-time tracking[C]//, Las Vegas, NV, USA, 2016: 1401–1409.

[24] Ma C, Yang X K, Zhang C Y,. Long-term correlation tracking[C]//, Boston, MA, USA, 2015: 5388–5396.

[25] Li Y, Zhu J K, Hoi S C H,. Robust estimation of similarity transformation for visual object tracking[Z]. arXiv: 1712.05231[cs.CV], 2017.

Adaptive multi-filter tracker based on efficient convolution operator

Li Guoyou, Zhang Fengxv*, Ji Zhian

Key Laboratory of Industrial Computer Control Engineering, Yanshan University, Qinhuangdao, Hebei 066004, China

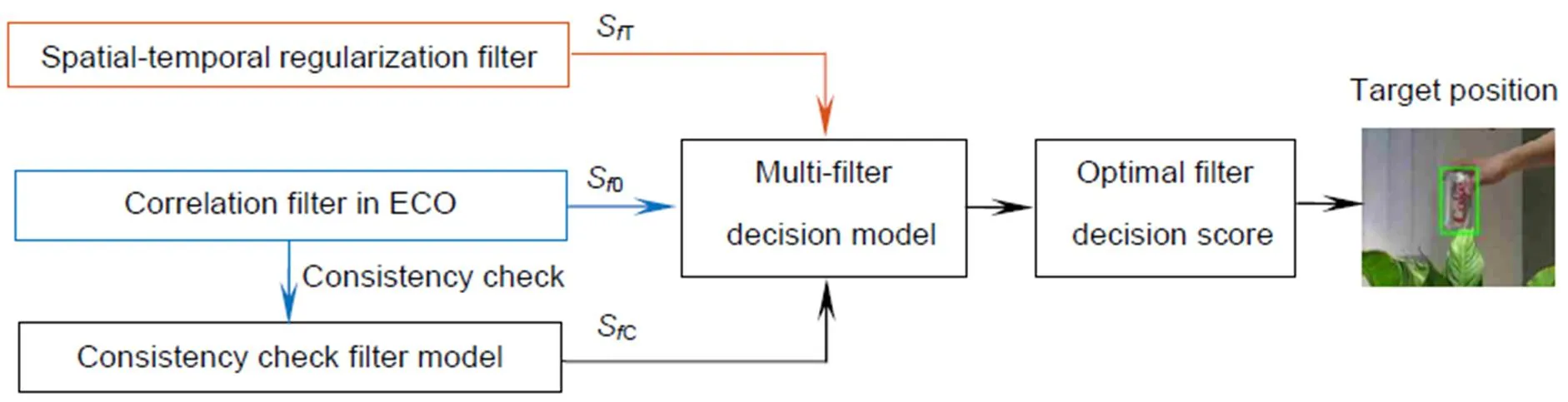
Multifilter decision flow chart

Overview:In the actual target tracking process, the shape and posture of the target are different, and the environment in tracking is complex and changeable. It is difficult for a single filter to cope with the complex changes of the video sequence and tracking environment. To solve this problem, based on the efficient convolution operators for tracking algorithm, a multi-filter target tracking algorithm which can adapt to more complex environments is proposed. The algorithm trains two more filters of spatial-temporal regularization filter and consistency checking filter than the efficient convolution operators for tracking algorithm. The spatial-temporal regularization filter is obtained by introducing the temporal regularization into the loss function of correlation filtering. Spatial-temporal regularization filter can well adapt to the huge changes in the appearance of the target, so it can adapt to the environment that targets variable. The training method of consistency check filter is: firstly, the current filter is used to locate the target that has been tracked forward, and then the errors between the reverse location coordinate and the forward location coordinate are compared. When the error is less than the threshold, the consistency check filter is updated, but not be updated when the distance error is greater than the threshold. The consistency check filter reduces the noise information introduced in the filter update process, so it can be used in the case of more background clutter and noise. The correlation filter in the efficient convolution operators for tracking algorithm retains the most comprehensive target and background feature information, so it is suitable for relatively stable tracking environment with less interference. Spatial-temporal regularization filter, consistency check filter and correlation filter in efficient convolution operators for tracking are convolved with target features respectively, and three filter detection scores are obtained. The filter detection score obeys the Gaussian distribution. The higher the peak to side ratio of detection score, the higher the target tracking accuracy. The position of the target is estimated by the best filter detection score witch the peak to side ratio is more than the other filter detection score. The improved algorithm is evaluated on the OTB-2015 data set and UAV123 data set. Through qualitative and quantitative analysis, the experimental results show that the improved algorithm can better adapt to the complex changing environment in the tracking process, and its accuracy and success are improved, which is superior to most existing tracking algorithms.

Citation: Li G Y, Zhang F X, Ji Z AAdaptive multi-filter tracker based on efficient convolution operator[J]., 2020, 47(7): 190510

Adaptive multi-filter tracker based on efficient convolution operator

Li Guoyou, Zhang Fengxv*, Ji Zhian

Key Laboratory of Industrial Computer Control Engineering, Yanshan University, Qinhuangdao, Hebei 066004, China

With the problem of difficulty that a single filter to adapt to various complex changes in the tracking process, an adaptive multi-filter target tracking algorithm based on the efficient convolution operators for tracking is proposed. Spatial-temporal regularized filter, the consistency check filter and the correlation filter in the efficient convolution operator tracker, convolve with target features respectively, which obtains three detection scores. The training method of spatial-temporal regularized filter is to introduce temporal regularization into loss function. The consistency check filter is a filter that uses current filter to track the target of previous several frames and updates only when the error of forward and backward position is less than the threshold. Target position is estimated by the best filter detection score with the peak-to-side ratio is maximum. The improved algorithm is tested with the OTB-2015 dataset and UAV123 dataset. The experimental results show that the proposed algorithm can better adapt to the complex environment in tracking process, which has high precision and robustness.

target tracking; filter; spatial-temporal regularized; consistency check; efficient convolution operators

TP391.4

A

10.12086/oee.2020.190510

: Li G Y, Zhang F X, Ji Z A. Adaptive multi-filter tracker based on efficient convolution operator[J]., 2020,47(7): 190510

李国友，张凤煦，纪执安.自适应多滤波器的高效卷积算子目标跟踪算法[J]. 光电工程，2020，47(7): 190510

Supported by Youth Fund for Science and Technology Research in Colleges (2011139), and Universities of Hebei Province and Natural Science Foundation of Hebei Province (F2012203111)

* E-mail: 1097089954@qq.com

2019-08-31；

2019-12-27

河北省高等学校科学技术研究青年基金项目(2011139)；河北省自然科学基金项目(F2012203111)

李国友(1972-)，男，博士，教授，主要从事机器视觉和图像处理算法的设计。E-mail：lgyysu@163.com

张凤煦(1994-)，男，硕士研究生，主要从事运动目标的检测与跟踪的研究。E-mail：1097089954@qq.com