工业产品表面高精度三维测量方法的研究

孙 亮，韩勇华，王剑涛，王轶骁，朱 涟，伏燕军*

(1.南昌航空大学，330063，南昌； 2.南昌航空大学无损检测技术教育部重点实验室，330063，南昌)

0 引言

随着数字图像处理、人工智能以及计算机科学的高速发展，基于条纹投影的三维测量[1-2]方法，由于其具有非接触、高速、高精度和全场测量[3]等优势被广泛应用。目前基于条纹投影的三维测量方法在很多领域有着广泛应用，例如，安防监控领域[4-5]、生物医学领域[6-7]以及工业在线监测领域。在条纹投影的三维测量基础中，通过将预先设计好的正弦条纹由DLP投影仪投射到物体表面，被物体调制后的变形条纹由相机接收并送至计算机，经过求解包裹相位和相位展开得到带有物体高度信息的相位值，再经过系统标定后就可以得到物体的三维形貌。

傅立叶变换法[8-9]和相移法[10-11]是常见的包裹相位获取方法。傅立叶变换法求解包裹相位虽然只需一幅条纹图，但其精度比相移法要低。而相移法对环境光和随机噪声不敏感，求解的包裹相位精度高，但是在测量系统中，采集条纹图使用的DLP投影仪和CCD相机多为非线性设备，正弦条纹不具有较好的正弦性，从而导致求解的相位仍然存在一定误差。这种非线性效应是影响投影测量系统精度的主要因素。

Jia[12]提出了一种新型高速两步相移法用于三维测量，该方法只需要投影2个相移180度的三角形条纹图，通过计算2个捕获的三角形条纹图得到强度比就可以对物体进行三维重建。Dai[13]等利用三步相移算法获得包裹相位时发现测量精度会被存在的高次谐波影响，提出了利用具有周期性和对称性的二元图案来产生高质量的条纹图案。Xu[14]等人为了减轻高次谐波的影响，提出了一种被动误差补偿的方法，但是如果条纹宽度过大，这个方法会受到限制。Flores[15]提出了一种合成三角波条纹的方法，可有效解决投影仪非线性伽马引起的问题。Huang[16]提出了一种可以明显地减小该相位误差的双三步相移算法，需要2组初始相位差设计为60°的正弦光栅条纹投影图(每组3幅图)，相位误差可以得到明显的改善，实验证明，该方法能有效地削弱非线性误差对条纹投影测量系统的影响。在实际测量中，双四步相移算法由于相位误差的正弦周期与相移算法的相移步数有关，且初始相位的差值设计为45°，更能够有效地减小测量误差。实际上，系统中存在的噪声、环境光以及离焦程度等因素都会造成不同程度的相位误差[17-20]。而基于相位而不是强度的相位编码方法[21]对环境光、相机噪声和测量物体表面的对比度等因素不敏感，具有良好的抗干扰能力和较强的鲁棒性。由于双四步相移算法[22]仍然具有四步相移算法抗噪性的优点，从中得到的融合相位[22]需进行相位展开，提出了一种双四步相移结合相位编码的三维测量方法，较于传统的相移结合相位编码的方法，该方法可以进一步抑制非线性误差对测量带来的影响，提高测量的精度。实验结果表明了该方法的可行性和有效性。

本文其余部分结构如下。第1部分介绍了双四步结合相位编码的原理。第2部分通过实验证实方法的可行性。第3部分总结本文。

1 原理

1.1 测量系统原理

如图1所示为基于结构光的三维测量系统，该系统由投影仪、工业CCD相机、计算机、参考平面组成。相机光轴与参考平面垂直，然后投影仪光轴和相机光轴相交于参考平面上的O点，P为投影仪光心点，C为相机光心点，两点在同一高度，d为两点之间的距离，两点到参考平面的距离为l。其中参考平面上正弦条纹频率为f，物体表面图像和参考平面图像对应点的连续相位差为△φ。则下列计算公式(1)是被测物体某点M的高度：

(1)

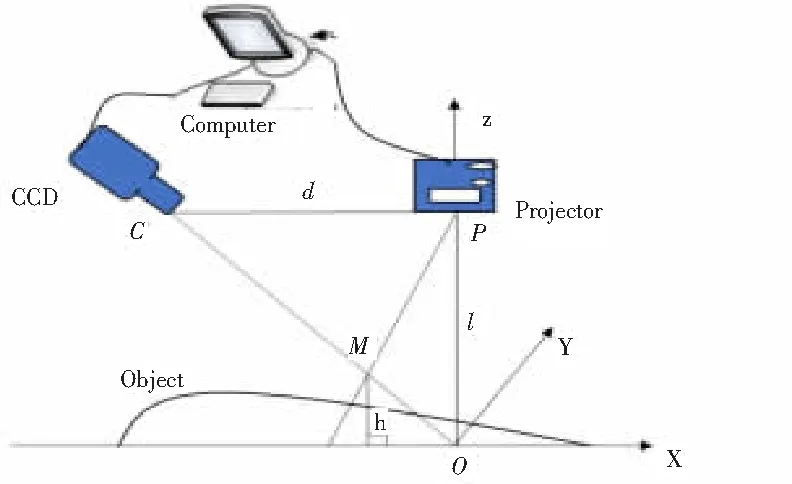
图1 三维测量系统原理图

1.2 双四步相移原理

针对N步相移算法[23]的第i个正弦条纹图案可以表示为：

Ii(x,y)=Ia(x,y)+Ib(x,y)cos[φ(x,y)+δi]

(2)

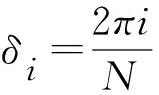
对待求相位φ(x,y)进行傅立叶级数展开获得实际相位φ′(x,y)，则△φ(x,y)=φ′(x,y)-φ(x,y)，根据三角函数获得：

(3)

则相位误差相位函数△φ(x,y)为：

(4)

传统的四步相移算法所对应的相位误差函数可以近似表示为：

△φ(x,y)≈c1sin[4φ(x,y)]

(5)

式中c1为一个常数。

在投影N幅正弦条纹图中，外加一个初始相位∂，设计好的正弦条纹图则可以描述为：

Ii(x,y)=Ia(x,y)+Ib(x,y)cos[(φ(x,y)+∂)+δi]

(6)

式中：[φ(x,y)+∂]为上述正弦条纹图的初始相位。则此时的四步相移算法中，可以近似表示相位误差为：

△φ′(x,y)≈-c2sin{4[φ(x,y)+∂]}=-c2sin[4φ(x,y)+4∂]

(7)

当条纹图未引入额外的初始相位，即∂=0时，实际相位分布对应的相位误差为△φ(x,y)，此时的实际相位可表示为：

(8)

而当∂=π/4时，相位误差为：

△φ′(x,y)≈-c2sin[4φ(x,y)+4×π/4]=c2sin[4φ(x,y)]=-△φ(x,y)

(9)

则可以由2种形式表示此时实际主值相位分布：

(10)

(11)

(12)

1.3 相位编码原理

Wang在2012年首次提出相位编码[24]的方法，利用一组正弦条纹和一组相位编码条纹即可实现相位解包裹，使用相位代替强度来确定码字，增强了其鲁棒性。相位编码方法中的编码相位需预先设计好并嵌入到相位编码条纹中去，通过一系列计算可确定条纹级次，求得条纹级次与包裹相位的周期一一对应。传统相位编码原理流程如图2所示。

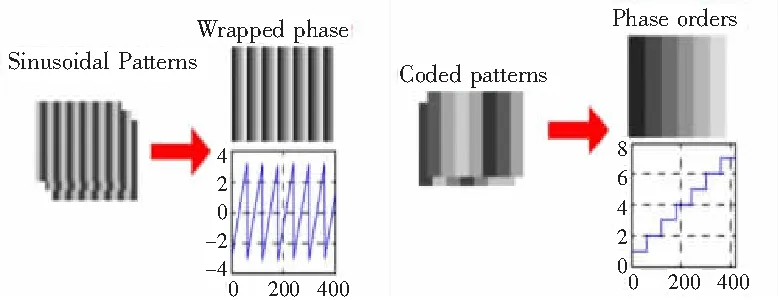
图2 相位编码原理流程图

1)设计阶梯编码相位，初始相位由式(13)生成：

(13)

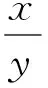
2)根据式(14)生成相位编码条纹：

Ak(x,y)=a(x,y)+b(x,y)cos[φs(x,y)+2π(k-1)/4]

(14)

式中：a(x,y)是平均强度，b(x,y)是调制强度，这里，k=1、2、3、4。

正弦条纹图案和相位编码条纹图案如图3所示。

(a)四步相移条纹 (b)相位编码条纹图

3)从相位编码条纹图中获得被编码在-π到+π的范围内的阶梯相位φs(x,y)。阶梯相位可利用式(15)计算获取：

(15)

4)根据获取的阶梯相位确定条纹级次k(x,y)：

k(x,y)=Round[N(φs(x,y)+π)/2π]

(16)

式中Round[·]为确定最接近的整数。

5)条纹级次k(x,y)确定后，就可以进行相位展开。根据式(17)将包裹相位φ(x,y)转换为绝对相位Φ(x,y)。

Φ(x,y)=Φ(x,y)+2π×k(x,y)

(17)

2 实验

为了验证该方法的性能，搭建了一个测量系统，包括一个投影仪(DLP Light Crafter 4500)、一个CMOS摄像机(Basler acA1600-20gm GigE)和一台计算机，如图4所示。投影仪分辨率为1 140×912，摄像机分辨率为1 280×1 024。在接下来的实验中，正弦条纹图和相位编码图选择周期为32个像素。系统采用参考文献[25]中的方法进行标定。

图4 三维测量系统图

2.1 模型测量实验

为了验证本方法的可行性，测量了一个乌龟玩具模型。在实验过程中，相移步数N取4，由计算机得到的四步相移正弦条纹图案和四步相位编码图案被依次投影到待测的乌龟玩具模型的表面上，并且乌龟玩具模型调制的条纹图像用相机顺序地采集。其中，图5(a)是模型的四步相移正弦条纹图案的其中1幅，图5(b)为4幅相位编码条纹图的其中1幅，从中可以计算出整数型编码相位。如图5(c)所示是通过双四步相移可以获得融合相位。条纹级次k(x,y)从被调制后的相位编码图案中计算出，图5(d)为融合相位和条纹级次图的某一行。最终，通过高度公式，如图5(e)和(f)所示可以获得乌龟玩具模型的三维重建结果。从图5中可以看出，在乌龟玩具的模型眼睛部位和背部有一些凹凸不平区域，也同样可以被很好地复原出来。

(a)四步相移条纹图的其中1幅 (b) 4幅相位编码条纹图的其中1幅

3 结论

基于传统的相移结合相位编码的方法，由于系统中非线性响应的影响，所测得的相位信息存在误差，降低了测量精度。提出的一种双四步相移结合相位编码的三维测量方法，只需投影传统相移算法2倍相移光栅的双四步相移算法具有四步相移算法良好的抗噪性优点，2幅包裹相位图通过2次四步相移算法计算获得，经过相位融合得到融合相位。而相位编码的方法对环境光以及系统的噪声等因素具有较好的鲁棒性，对条纹级次的准确判断有利，可以获得比较理想的测量精度。相对于传统的相移结合相位编码的方法，该方法可以进一步抑制条纹投影轮廓术非线性测量误差对测量带来的影响。综上所述，该方法能对孤立复杂物体进行测量，且容易实现，更加有效，实验表明了该方法的可行性。