基于RSM和NSGA-Ⅱ的苜蓿种子离散元模型参数标定

马文鹏 尤 泳 王德成 尹世杰 郇晓龙

(中国农业大学工学院， 北京 100083)

0 引言

离散元法(Discrete element method, DEM)在农业装备研发中应用越来越广泛,采用离散元法研究散粒体动力学已成为一种发展趋势[1-2]。在排种器工作过程中，种间相互作用关系复杂，应用离散元法对排种过程进行数值模拟，有助于揭示排种机理，进而优化排种参数和性能[3-6]。紫花苜蓿是一种优质牧草，可以为畜禽提供优质饲料，被誉为“牧草之王”[7-9]。优化苜蓿种子离散元模型和仿真参数，可提高离散元法在苜蓿排种器研究中的准确性。物料物性参数主要包括本征参数和接触参数，本征参数是物体自身的特性参数(如泊松比、弹性模量和密度等)，颗粒间及颗粒与几何体间的接触参数包括碰撞恢复系数、静摩擦因数和滚动摩擦因数，是两个物体发生接触时的物性参数。大多数离散元模型的本征参数与真实参数数值一致，但由于颗粒模型的误差以及颗粒间复杂的接触特性，应对部分参数进行重新标定及优化[10-12]。

目前，国内外学者已完成土壤、稻谷、饲料和玉米等离散元模型的建立和仿真参数的标定。于庆旭等[13]基于粘结颗粒模型,以堆积角实测值与仿真值相对误差为指标，对三七种子离散元模型进行了接触参数标定。鹿芳媛等[14]利用内部坍塌法、侧壁坍塌法和重力平衡法获取了水稻芽种两种休止角及滑动摩擦角，通过仿真试验与实际试验相结合的方法，对不同含水率水稻芽种离散元的主要接触参数进行了标定。王云霞等[15]利用两种接触材料(有机玻璃板与铝质圆筒)进行玉米种子堆积角仿真试验，建立种间静摩擦因数和种间滚动摩擦因数两个自变量的二元回归方程，以实际测量种群堆积角作为已知目标量进行数值求解，求得EDEM中玉米种间摩擦因数。张涛等[16]以堆积角、最大静摩擦因数以及碰撞恢复系数为指标，标定大豆种子离散元模型与排种盘、搅种轮和有机玻璃间接触参数。张锐等[17]以实际堆积角为指标，对标准球型和非标准球型沙土颗粒接触参数进行了标定。彭飞等[18]提出一种基于注入截面法的休止角测定装置与方法，可通过颗粒堆积体截面的轮廓线直接获取休止角，并以此进行颗粒饲料离散元模型接触参数组合的优化。罗帅等[19]提出了通过测定基质含水率预测休止角的方法，并以休止角作为参照对蚯蚓粪基质离散元模型进行参数标定。GHODKI等[20]建立了大豆离散元模型，通过对大豆形状、静止角等特征进行比较，获得了该模型的接触参数。WANG等[21]将离散元法与物理试验相结合，以堆积角为指标对不规则形状玉米颗粒的滚动摩擦因数进行了标定。MOUSAVIRAAD等[22]通过休止角对比试验，优化了玉米离散元模型的形状和接触参数，并利用螺旋输送机的流量进行了验证。

目前，在针对离散元模型参数标定的研究中，多以单一的休止角或堆积角为试验指标，且标定结果仅为一组解。因此，提高标定试验效率、建立多指标参数优化数学模型，并使用更有效的优化方法对其进行求解，对于获取更精确的模型参数具有重要的现实意义。本文设计一种可同时测定物料休止角和堆积角的装置，并提出测试方法。以苜蓿种子为研究对象，进行实际落种与仿真落种试验，以休止角相对误差和堆积角相对误差为试验指标，通过Plackett-Burman试验筛选出对指标影响显著的接触参数，采用响应面分析法(RSM)建立显著性参数与各指标之间的二阶数学模型，利用非支配排序遗传算法Ⅱ(NSGA-Ⅱ)进行多目标寻优计算，获取更具有收敛性和多样性的Pareto最优解集，并进行排种验证试验，以期为苜蓿、黑麦草等小粒牧草种子离散元模型参数标定提供参考。

1 苜蓿种子离散元模型参数标定

休止角和堆积角是表征颗粒物料流动、摩擦等特性的宏观参数，与接触材料和物料本身物理特性有关[23]，因此可将其应用于离散元模型的接触参数标定试验中。

1.1 实际落种试验

落种试验装置如图1a所示。该装置主要由种箱、挡板和圆盘组成，试验材料为中苜一号紫花苜蓿种子。试验时，先关闭挡板，在种箱中均匀加入适量种子，约占种箱总容积的2/3，并尽可能保证种子层上表面的水平，将挡板快速打开，苜蓿种子在重力作用下落入圆盘，种箱内两侧对称形成梯形种堆。休止角θ为种箱上部水平面与种堆斜面所夹锐角；堆积角φ为种箱下部圆盘中水平面与种堆斜面所夹锐角，如图1b所示。

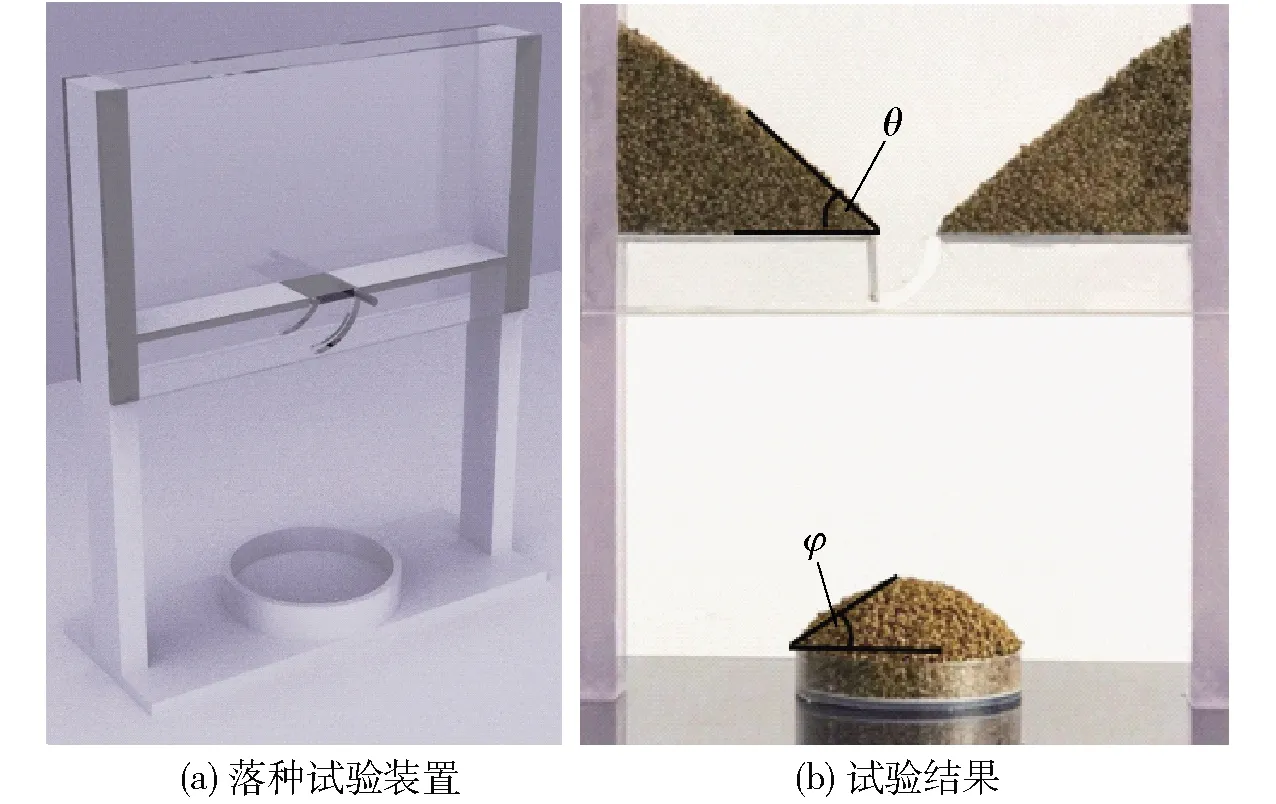
图1 实际落种试验Fig.1 Practical seed-dropping test

为减少人为测量导致的误差，利用Matlab软件对采集到的休止角和堆积角图像依次进行去噪处理、灰度处理以及二值化处理，获取种堆边界点，其连线即种堆边界曲线，最后采用最小二乘法对曲线进行拟合，得到一条直线，直线的斜率即苜蓿种子的实际休止角和堆积角的正切值，如图2所示,其中左图为休止角，右图为堆积角。每组试验重复5次取平均值(表1)，得到实际试验中紫花苜蓿种堆休止角和堆积角平均值分别为40.64°和31.28°。

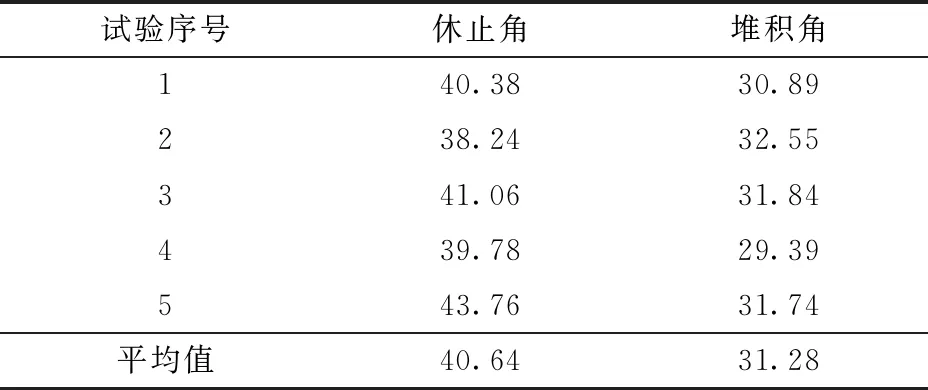
表1 紫花苜蓿实际条件下休止角和堆积角测量结果Tab.1 Measurement results of repose angle and accumulation angle of alfalfa under actual conditions

1.2 落种仿真试验

根据苜蓿种子的物理特性(表2)，在EDEM软件中利用球形颗粒组合的方法建立苜蓿种子仿真模型，如图3所示。颗粒接触模型选取Hertz-Mindlin无滑移模型[24-25]。将测量装置的几何模型和苜蓿种子模型导入EDEM中，设置苜蓿种子数量、试验过程与真实试验相同，试验结束后对堆积角进行图像采集，同样利用Matlab处理图像，获取仿真休止角β与堆积角γ，如图4所示。休止角误差Y1和堆积角误差Y2的计算公式为

(1)

(2)

表2 中苜一号紫花苜蓿种子物理特性参数Tab.2 Alfalfa seed physics features

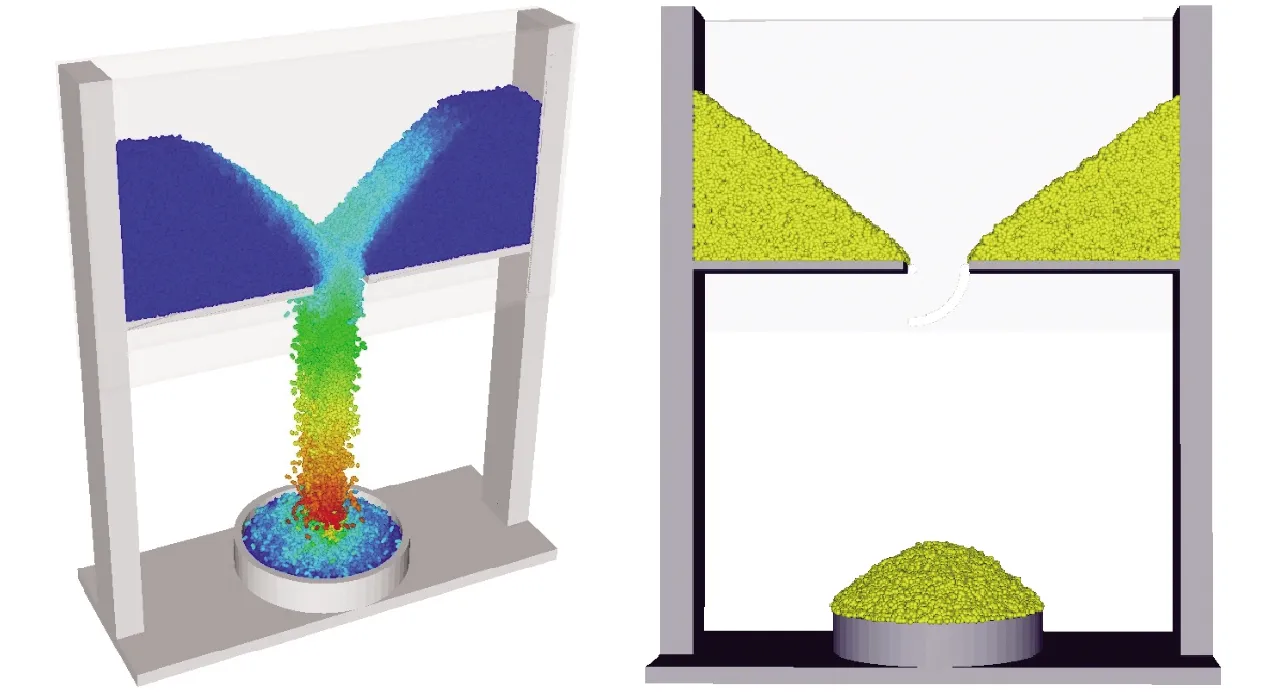
图4 落种仿真试验Fig.4 Simulated seed dropping test

1.3 Plackett-Burman试验

应用Design-Expert软件设计Plackett-Burman试验，以苜蓿种群休止角误差和堆积角误差为响应值，筛选出对响应值影响显著的仿真参数。仿真试验中共7个真实参数A～G，设置4个虚拟参数H～K，每个参数按照推荐范围值均取低、高2个水平，分别以编码-1和1表示。根据文献[13-14]以及前期大量预试验对各参数范围进行选取，结果如表3所示。仿真试验中设定1个中心点，共进行12组试验，每组仿真试验重复4次，取平均值，并计算休止角误差和堆积角误差。

表4为Plackett-Burman试验的设计方案及仿真结果，采用Design-Expert 软件对该模拟试验结果进行方差分析，得出各参数的影响效果如表5所示。

表3 Plackett-Burman 试验参数Tab.3 Test parameters of Plackett-Burman

由表5可知，种间碰撞恢复系数E、种间静摩擦因数F和种间滚动摩擦因数G对休止角误差、堆积角误差影响显著，其余参数影响较小。因此在最陡爬坡试验以及正交试验中对E、F、G3个影响显著的接触参数进行优化。

1.4 最陡爬坡试验

表6所示为最陡爬坡试验设计方案及结果，结果表明：随着种间碰撞恢复系数、种间静摩擦因数和种间滚动摩擦因数的增大，休止角误差和堆积角误差呈现先减小后增大的趋势，取试验3为中心点，设为中水平，选取试验2、4水平分别为低、高水平进行三因素二次旋转正交组合试验和回归模型分析；种间碰撞恢复系数、种间静摩擦因数以及种间滚动摩擦因数的优化范围分别为0.36～0.54、0.16～0.34、0.050～0.100。

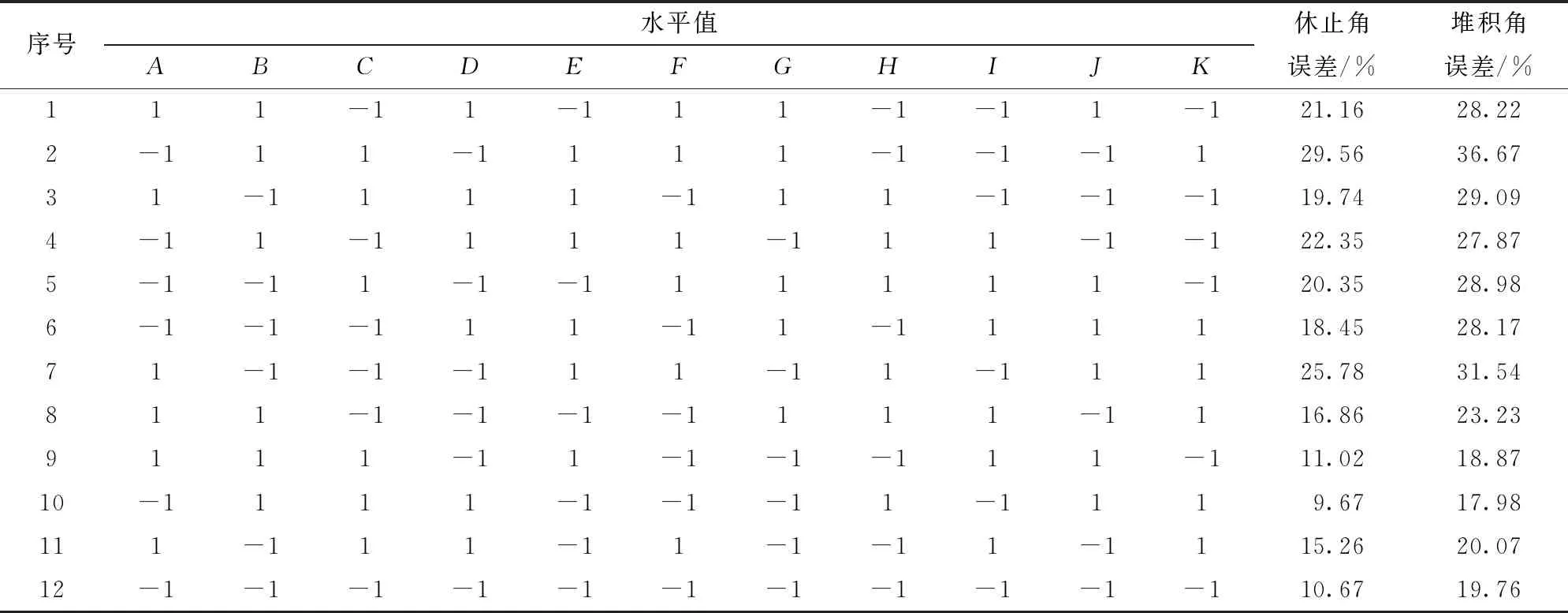
表4 Plackett-Burman试验方案设计及结果Tab.4 Design and results of Plackett-Burman test scheme

表5 Plackett-Burman 试验参数显著性分析Tab.5 Significance analysis of Plackett-Burman test parameters

表6 最陡爬坡试验设计方案及结果Tab.6 Test design scheme and results of steepest climb

1.5 三因素二次旋转正交组合仿真试验

为进一步获取最优接触参数组合，以种间碰撞恢复系数、种间静摩擦因数和种间滚动摩擦因数为试验因素，以休止角误差和堆积角误差为试验指标，进行三因素二次旋转正交组合仿真试验。试验因素编码见表7，试验方案与试验结果见表8(e、f、g为因素编码值)，每组试验重复5次取平均值。

表7 仿真试验因素编码Tab.7 Simulation test factors and codes

表8 试验设计方案及响应值结果Tab.8 Test design scheme and response value results

1.6 多目标优化方法

本文选取种间碰撞恢复系数、种间静摩擦因数和种间滚动摩擦因数进行优化，设有两个响应值，因此属于多目标优化研究。对于多目标优化问题，通常存在一个最优解集，被称为Pareto最优解。首先应用RSM法进行正交试验，建立参数与目标之间的关系，之后利用NSGA-Ⅱ算法进行全局搜索，得到Pareto最优前沿。NSGA-Ⅱ算法是由DEB提出的一种在多目标遗传算法界非常有效，并基于非支配排序、精英保留策略与多样性维持机制的优化算法，该算法所特有的精英保留策略和多样性维持机制可以确保其计算结果的收敛性与多样性[26-27]。NSGA-Ⅱ算法流程如图5所示，优化步骤如下：①确定待优化的接触参数以及试验指标。②利用RSM进行试验设计。③从落种仿真试验中获取数据。④对试验结果进行二次方差分析，建立有目标因素的回归模型。⑤利用NSGA-Ⅱ算法计算Pareto最优前沿，得到最优过程。⑥通过排种试验验证最佳工艺参数。

图5 NSGA-Ⅱ算法流程图Fig.5 Flow chart of NSGA-Ⅱ algorithm

2 试验结果与讨论

2.1 数学模型的建立与显著性检验

2.1.1休止角误差回归模型与显著性检验

通过试验以及对试验数据进行多元回归拟合，得到各因素对休止角误差影响的回归模型

Y1=173.771 64-468.323 57E-255.367 7F- 803.419 22G+175.903 72EF-234.130 91EG+ 215.274 73FG+466.093 77E2+354.365 37F2+ 5 472.575 2G2

(3)

回归方程的显著性检验如表9所示，根据表9可知，该模型的拟合度是极显著的(P<0.01)。其中E、F、G、EF、E2、F2以及G2的P值均小于0.05，说明以上各项对休止角误差的影响显著，相关试验因素对响应值的影响存在二次关系。对于失拟项P=0.464 3，不显著，说明不存在其他影响指标的主要因素存在。

2.1.2堆积角误差回归模型与显著性检验

通过试验以及对试验数据进行多元回归拟合，得到各因素对堆积角误差影响的回归模型

表9 回归方程方差分析Tab.9 Variance analysis of regression equation

Y2=157.903 25-247.843 26E-515.660 2F- 915.713 49G+356.608 79EF-105.280 34EG+ 42.426 41FG+193.728 02E2+683.234 19F2+ 5 950.715 16G2

(4)

回归方程的显著性检验如表9所示，根据表9可知，该模型的拟合度极显著(P<0.01)。其中E、F、G、EF、E2、F2以及G2的P值均小于0.05，说明以上各项对休止角误差的影响显著，相关试验因素对响应值的影响存在二次关系。对于失拟项P=0.064 3，不显著，说明不存在其他影响指标的主要因素存在。

2.2 各因素对试验指标的影响

2.2.1各因素交互作用对休止角误差的影响

对数据进行处理，可得到种间碰撞恢复系数、种间静摩擦因数和种间滚动摩擦因数对休止角误差的影响，其响应曲面如图6所示。由图可知，等高线呈现较大曲率的椭圆形，各因素交互影响显著。在种间碰撞恢复系数为0.42～0.48、种间静摩擦因数为0.22～0.28、种间滚动摩擦因数为0.068～0.082时，休止角误差较小。

2.2.2各因素交互作用对堆积角误差的影响

各因素对堆积角误差交互作用的响应曲面如图7所示。由图可知，种间静摩擦因数与种间滚动摩擦因数对堆积角误差影响较显著，在种间静摩擦因数为0.22～0.28、种间滚动摩擦因数为0.068～0.082时，休止角误差较小。

2.3 NSGA-Ⅱ算法优化

本文以最小休止角误差和最小堆积角误差为优化目标，以种间碰撞恢复系数、种间静摩擦因数和种间滚动摩擦因数为优化对象进行研究。在最陡爬坡试验的基础上，确定种间碰撞恢复系数为0.36～0.54，种间静摩擦因数为0.16～0.34，种间滚动摩擦因数为0.05～0.10。因此，优化问题的目标函数和约束函数为

(5)

用NSGA-Ⅱ算法求解优化模型得到的Pareto最优解曲线如图8所示。对于多目标优化问题，不可能使每个目标同时最优。但可以在目标之间进行协调和权衡，以尽可能地满足每个目标，这意味着最优边界上的所有解都可以用于方案优化。在兼顾休止角误差和堆积角误差的原则下，选取种间碰撞恢复系数为0.47，种间静摩擦因数为0.24，种间滚动摩擦因数为0.08，此时休止角误差为1.687%，堆积角误差为1.683%。

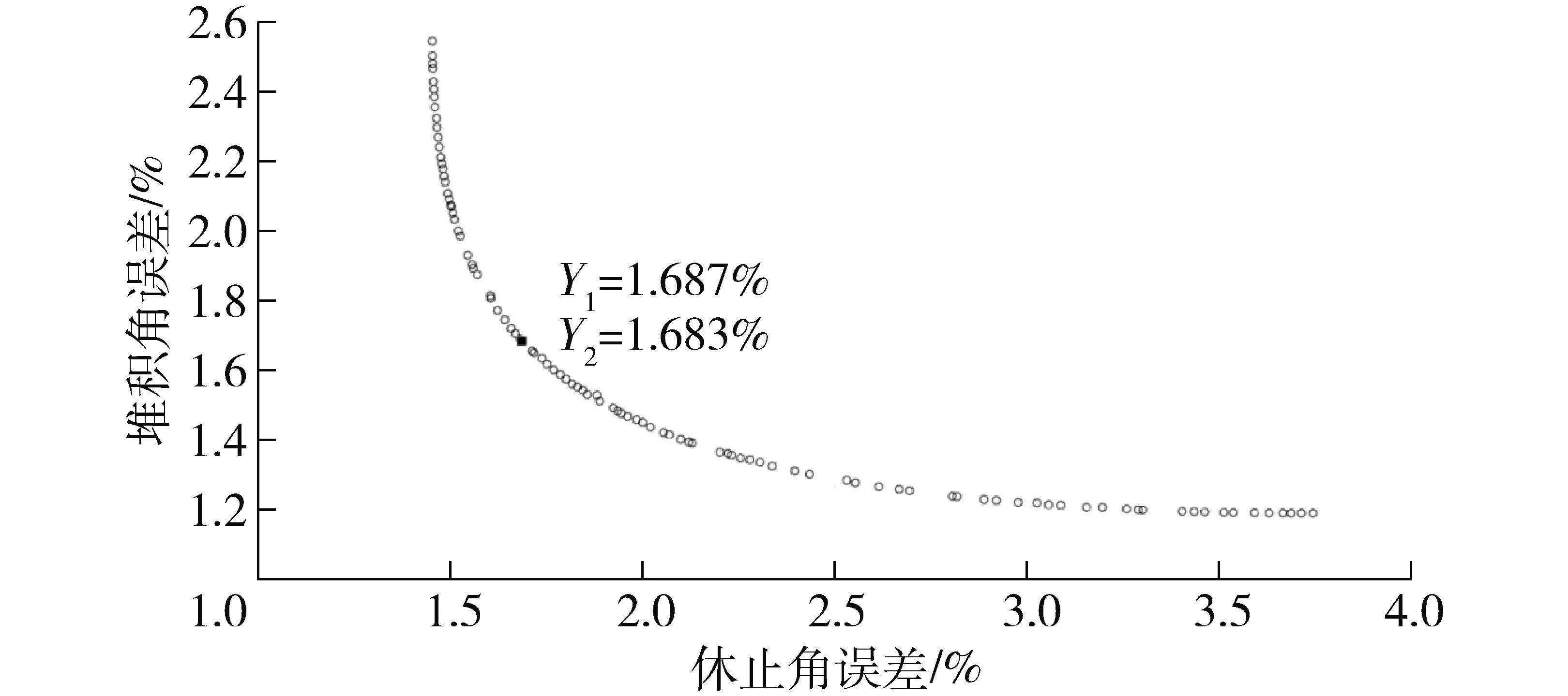
图8 基于NSGA-Ⅱ的Pareto最优解曲线Fig.8 Pareto optimal set based on NSGA-Ⅱ

3 验证试验

为进一步验证苜蓿离散元模型和仿真参数的可靠性，采用槽轮式排种器进行试验验证，以排种质量流率为试验指标，在不同排种轮转速条件下(10～60 r/min)对比质量流率的实测值和仿真值。选取中苜一号苜蓿种子进行台架试验，排种轮采用3D打印，台架如图9a所示。试验时，首先在种箱中加入适量紫花苜蓿种子，打开步进电机的电源，调节电机转速，种子下落至排种器下方的收集盘中，待种子均匀排出时，每隔1 min记录1次圆盘中种子的质量，计算排种器的质量流率，重复5次取平均值。将排种器的简化模型、苜蓿种子离散元模型和标定的接触参数导入离散元软件EDEM中，在与台架试验相同条件下进行仿真试验，输出排种器质量流率，仿真试验如图9b所示。

图9 验证试验Fig.9 Verification test

图10为不同转速条件下质量流率的实测值和仿真值。由图可知，质量流率的实测值和仿真值与排种轮转速的变化趋势一致，两者平均相对误差为2.89%，表明该苜蓿离散元模型和接触参数可用于离散元仿真试验。

图10 不同转速条件下质量流率的实测和仿真结果Fig.10 Measured and simulated values of mass flow rate at different rotational speeds

4 结论

(1)设计了一种可同时获取物料休止角与堆积角的装置，以苜蓿种子为研究对象，通过实际落种试验，并采用Matlab数字图像处理技术，测定苜蓿种子休止角为40.64°、堆积角为31.28°。

(2)采用Hertz-Mindlin无滑移模型以及球面堆积法，在EDEM软件中建立苜蓿种子离散元模型，并进行了落种仿真试验；以休止角相对误差和堆积角相对误差为试验指标，进行Plackett-Burman试验，筛选出对指标影响显著的3个因素分别为：种间碰撞恢复系数、种间静摩擦因数、种间滚动摩擦因数。以这3个因素为试验因素，以休止角误差和堆积角误差为试验指标，进行了三因素二次旋转正交组合试验。通过方差分析可知，3个试验因素及其二次方项对休止角误差的影响显著(P<0.05)。对各因素指标的交互作用进行分析，并获得了因素与指标之间的回归数学模型。

(3)以最小休止角误差和最小堆积角误差为优化目标，以种间碰撞恢复系数、种间静摩擦因数和种间滚动摩擦因数为优化对象，采用NSGA-Ⅱ对回归数学模型进行求解，获取了Pareto最优解集。在兼顾休止角误差和堆积角误差的原则下，选取种间碰撞恢复系数为0.47、种间静摩擦因数为0.24、种间滚动摩擦因数为0.08，此时休止角误差为1.687%，堆积角误差为1.683%。

(4)采用槽轮式排种器进行试验验证，搭建排种试验台架进行实际排种试验，并在EDEM软件中进行仿真试验。结果表明，在不同排种轮转速下，苜蓿种子质量流率的实测值和仿真值平均相对误差为2.89%，该苜蓿种子离散元模型和接触参数可用于离散元仿真试验。