一类分数阶微分方程的数值解法

罗 芳，王振芳

(山西大同大学数学与统计学院，山西大同 037009)

在过去的几十年里，分数阶微积分有了显著的发展，这可以从许多专门的数学文献中看出。相应地，分数阶微分方程广泛地应用到科学和工程等领域，许多学者研究了分数阶微分方程解的存在与唯一性[1-3]。而大多数分数阶微分方程无法求得精确解析解，因而必须使用数值的方法。

针对区间(0,L)上的非线性分数阶初值问题，提出了移位Chebyshev 配置法。非线性微分方程在N个Chebyshev 点上进行配置，得到N个方程，连同n个初始条件一起得到具有(N+n)个方程的非线性代数方程组。然后利用适当的方法求解。

1 介绍

1.1 分数阶微积分

定义1σ阶Riemann-Liouville分数积分定义为

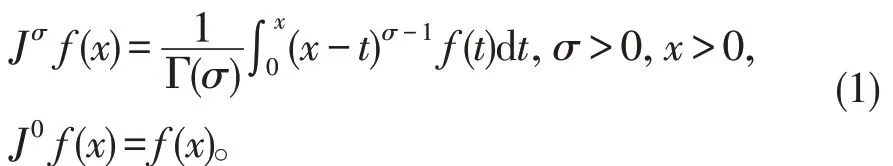
算符Jσ具有性质：

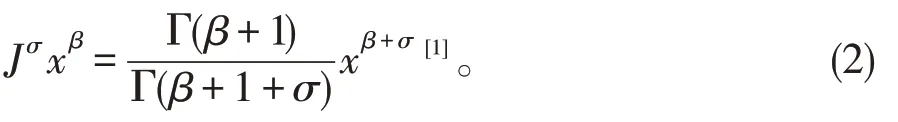
定义2σ阶Caputo分数导数定义为

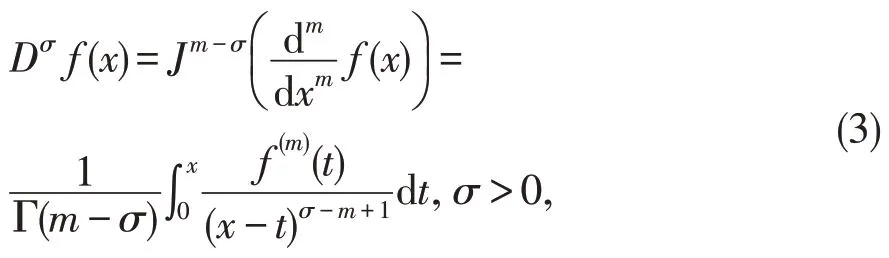
其中m-1 ＜σ≤m,m∈N[4-5]。

Caputo导数具有线性性，即

其中上限函数「σ」 表示大于或等于σ的最小整数，N0={0,1,2,…}[3]。

1.2 Chebyshev多项式

所谓标准Chebyshev 多项式是当区间为[-1,1]，权函数为时，由序列{1,t,…,tn,…}正交化得到的多项式，并且满足递推关系：

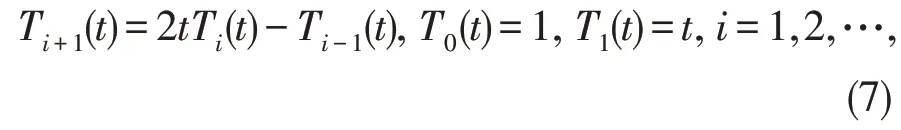
及正交性

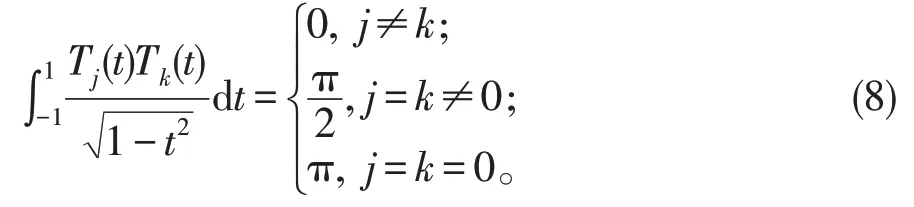
对于[-1,1] 上的任意连续函数u(t)，均可按Ti(t),i=0,1,2,…,表示为：

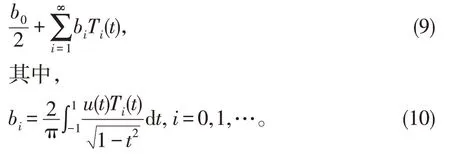
1.3 移位Chebyshev多项式的性质

当区间为x∈[0,L]时，将(7)中的t利用代替，则可得所谓移位Chebyshev 多项式TL,i(x)=相应地TL,i(x)的递归关系为:

其中TL,0(x)=1 且TL,1(x)=-1。而i次的移位Chebyshev多项式TL,i(x)由下式给出

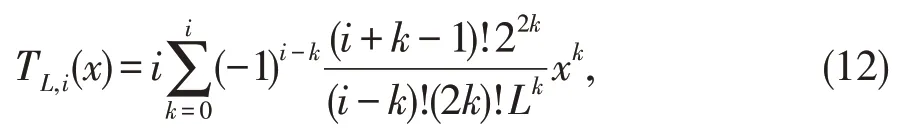
其中TL,i(0)=(-1)i且TL,i(L)=1。

其正交性为

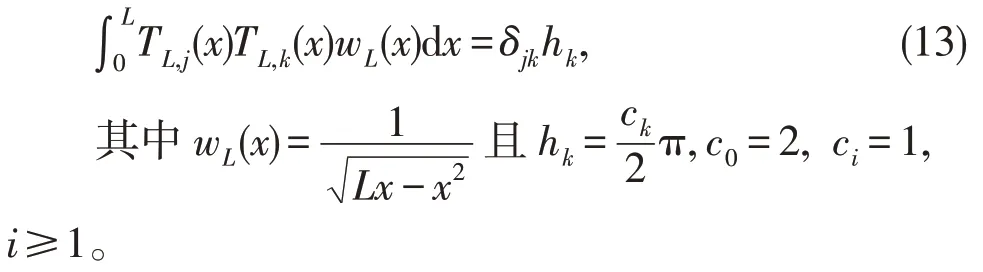
任何在[0,L]上平方可积可积函数u(x)，均可用移位的Chebyshev多项式表示为

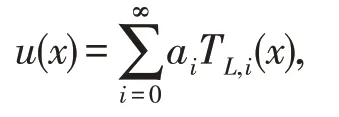
其中，系数ai为

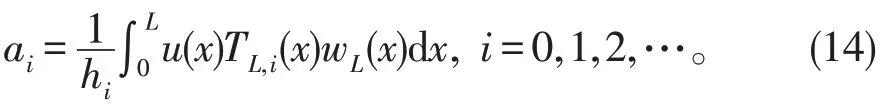
实际中常常只用到前N+1项。即

现在来处理移位的Chebyshev-Gauss 插值。用0 ≤j≤N表示区间(-1,1) 上标准Chebyshev-Gauss点，且

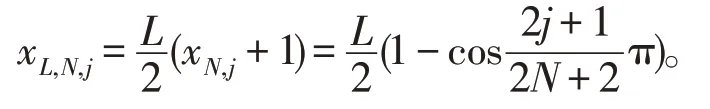
显然，xL,N,j,0 ≤j≤N是TL,N+1(x)的零点。

设PN(0,L)是次数不超过N的所有多项式的集合。标准Chebyshev-Gauss 公式意味着，对于任何φ∈P2N+1(0,L),有

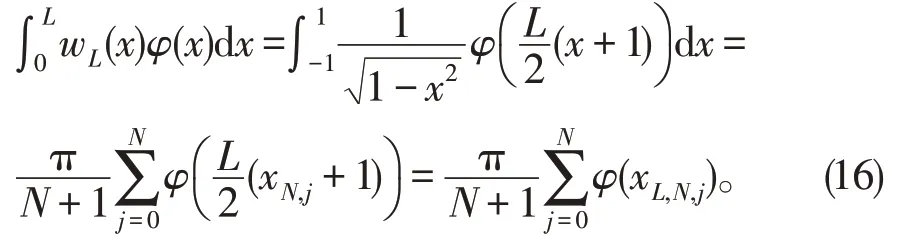
1.4 移位Chebyshev多项式的分数阶导数

定理1设TL,i(x)是移位的Chebyshev多项式，则

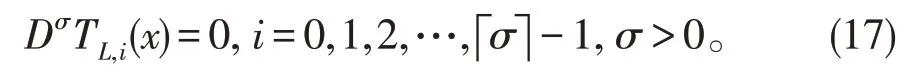
证明利用关系式(5)、(6)，可以证明这个定理[2,4]。

定理2Chebyshev 多项式Caputo 意义上ν阶的分数导数由下式给出

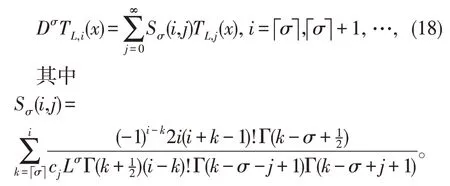
证明利用关系式(5)、(6)、(12)，可以证明这个定理，详见文献[2,4]。

2 分数阶初值问题的数值方法

考虑如下非线性分数阶微分方程

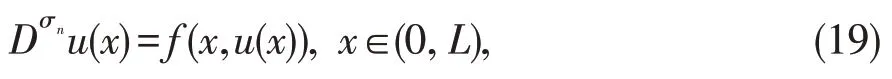
满足初始条件

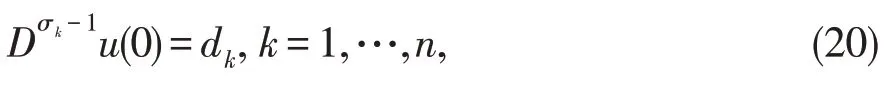
其中，

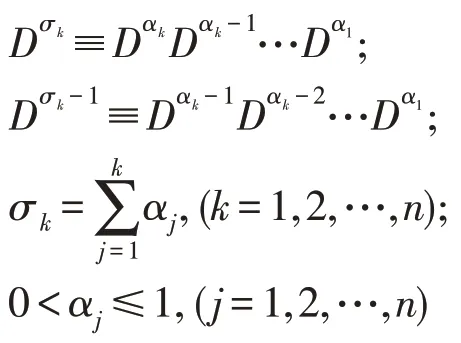
的数值解法。其中dk,k=1,…,n的值描述u(x)的初始状态，f(x,u)是定义在平面(x,u)的区域D上函数，且区域R(h,K)为满足不等式：

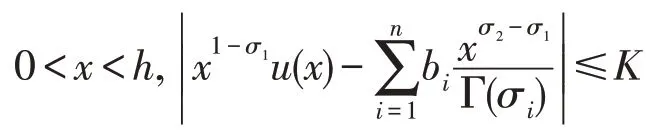
的点(x,u)∈D的集合，其中h和K为常数。

定理3设f(x,u(x))为定义在区域D上的实连续函数，在D上关于u满足Lipschitz条件，即

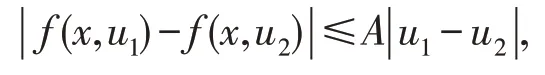
这样，对任意(x,u)∈D,|f(x,u) |≤M＜∞，且令

则在区域R(h,K)中存在问题(19)、(20)的唯一的连续的解u(x)。

证明详见文献[1]。

为了使用移位的Chebyshev 配置法来求解方程(19)、(20)。令

然后，利用公式(18)可以由展开系数aj明确地表示导数k=1,…,n,移位Chebyshev 配置法求方程(19)、(20)近似解的标准是找到uN(x)∈SN(0,L)，使得

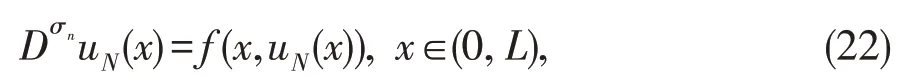
在配置点xL,N,k,k=0,1,…,N-1 处是准确的。换句话说，我们必须在N个移位Chebyshev 多项式的根xL,N,k处配置方程(19)、(20)，立即有

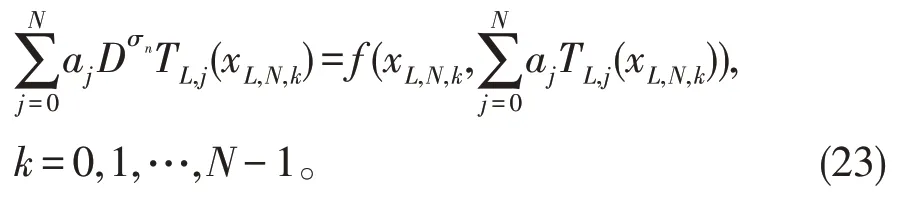
且初始条件写成

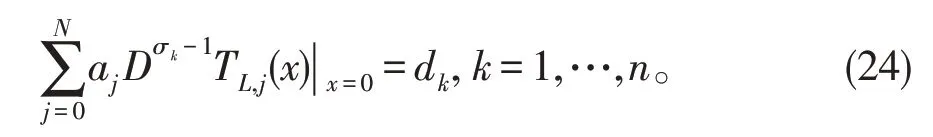
这构成了一个关于N+1个展开系数aj(j=0,1,…,N)的含有N+n个方程的超定非线性代数方程组，可以用任何数值方法(如最小二乘法)求解。

3 结论

根据移位的Chebyshev 多项式特点，给出了移位Chebyshev 多项式分数阶导数的显式表达式。此外，利用Chebyshev-Gauss 多项式近似给出了一类分数阶微分方程的数值解法。相应的也可以应用勒让德多项式或其它正交多项式。