绳索落地问题的两种算法对比分析

高彩云

（山西大同大学物理与电子科学学院,山西大同 037009）

从古到今，对于物体下落问题的探讨贯穿着物理学的发展。牛顿由苹果落地的联想发现了万有引力定律，伽利略比萨斜塔的实验反驳了亚里士多德统治多年的“重物先落至地”的观点，而爱因斯坦广义相对论等效性原理的得出，也是通过构建了自由下落的升降机的理想实验[1-3]。链条或绳索的下落作为变质量物体的典型体系，引入了力学和理论力学教科书作为范例，一直备受关注。现有的文献研究主要集中在两个方面：一是变质量物体的动力学方程的推导及意义，分别从质点系动量定理、质点动量定理出发，对方程的物理含义进行解析[4-6]，指出不能以牛顿第二定律的形式来代替变质量物体运动的动力学方程，从本质上说，后者是质点系动量定理的一种具体形式[7]；二是变质量物体运动方程的应用，比如是雨滴下落、火箭上升和链条（绳索）落地等，指出运用该方程时必须注意的关键问题，比如研究对象的选取，受力分析及各部分运动特征的分析[8]。其中，链条落地作为一个典型范例，文献[9]、[10]都涉及到链条竖直悬挂，起始时刻末端刚好与地面接触，那么在下落过程中的任意时刻它对地面的压力等于已经落下部分重力的3 倍。而文献[11]详细地分析了链条的下落运动的四种初始构型，并分析了它们下落运动所具有的有别于自由落体运动的特征。本文在研究现有文献的基础上，以绳索为例，着重探讨了运用质点动量定理和质点系动量定理两种不同的方法求解落地过程中任意瞬时绳索对地面的压力，解决教学中的一些困惑。

1 问题提出

一柔软、无弹性、质量均匀的绳索，竖直地自高处下落至地板，质量为M和长度为L，求当绳索剩在空中的长度等于x(x＜L) 时，它对地板的压力。设开始时，它的速度为零，下端离地板的高度为h[12]。建立模型如图1。

图1 绳索落地的简化模型

由于绳索质量均匀，假设其线密度为σ，则

首先绳索是柔软的，内部的约束为柔性体约束。将它看作一个连续微元体，各个微元之间只有拉力、没有压力，当它落地时，地面的作用力只能作用到与地面接触的那个微元上，而不沿着绳索向上传递，这一点不同于刚体。刚体落地时由于地面的撞击，各部分的速度都瞬间变为零，能量损失，而它此时对地面的压力，可以利用动量定理来求，但是又和地面的硬度等有很大关系。

其次绳索无弹性，各微元之间的作用力大小相等，所以内力互相抵消，如果忽略空气阻力，下落过程中只有重力的作用，那么绳索将作自由落体运动，且各处的速度相同，这一点又不同于弹簧等有弹性的绳索。弹簧在自由落体运动过程中，刚开始弹簧下部是不动的，弹簧从上面数第一圈开始逐渐地下落初始状态时，人手对弹簧一个拉力，这个拉力为弹簧的重力。当松开弹簧时，弹簧开始自由落体运动，顶圈的弹簧由于人手的拉力突然消失，弹簧的弹力依然存在，顶圈弹簧在自身重力和弹力的作用下加速下落（比自由落体快），随着顶部弹簧的下落，下面弹簧的弹力减小（对于特定的弹簧弹力和伸长量成正比，弹簧伸长量减小，弹力也减小），当弹力小于以下弹簧的自重时，弹簧开始下落，并且下降加速度逐渐增加。

2 两种算法对比与讨论

首先可以确定的是，绳索落地过程中任意瞬时对地面的压力应大于已经落下部分的重力，还有一部分正在落地微元对地面的冲力，且不能忽略，那么问题的关键就是求解这部分冲力。可以用质点系动量定理和质点动量定理两种方法求解。

2.1 运用质点系动量定理求解

2.1.1 动力学方程推导

绳索落地的过程中，是一个变质量问题，留在空中的部分质量不断减小，而落在地面的部分质量不断增加。下面推导其动力学方程。

设一个物体的质量为m，在t时刻具有速度v(v＜＜c)，此时，有一质量为Δm的微元以的速度u运动，二者在Δt时间后“合并”，合并以后具有共同速度v+Δv。如果整个过程中二者所受合外力为F，那么把它们看作是一个质点系，它们之间的内力大小相等、方向相反，因而消去，则根据质点系动量定理，有：

展开，并略去二阶微小量ΔmΔv，等式两边同时除以Δt，Δt→0，得到变质量物体的运动方程：

式中，F则为作用在质点系（即系统）上的合外力，u是微元Δm与物体m合并前一瞬间的速度，这种情况称为“合并问题”（例如雨滴下落），是物体质量的变化率，因质量不断增大，取正，当然，微元的在合并之前的瞬时速度可以为零，例如雨滴下落过程中不断凝结在它上面的水汽，这时，u=0，方程就简化为：

形式上和牛顿第二定律类似，不同的是这里的质量m是不断变化的；u也可以是微元Δm未与物体m分离以后一瞬间的速度，这种情况称为“分离问题”（例如火箭上升），这时是物体质量的变化率，因质量不断减小，取负。

根据上面推导的运动方程，就可以将绳索落地的问题看作是合并问题或者分离问题两种方法求解，落到地面上的绳索速度为零，首先需要计算剩在空中的部分此时具有的速度。

一维问题，取竖直向下为正方向。不考虑空气阻力，绳索的下落为自由落体运动，则此时剩余在空中的绳索具有的速度为：

2.1.2 合并问题

将已经落在地面上的绳索看作“主体”，正在与与地面接触的绳索看作微元，那么这就是“合并问题”，地面上的绳索质量在不断增大。如图2。

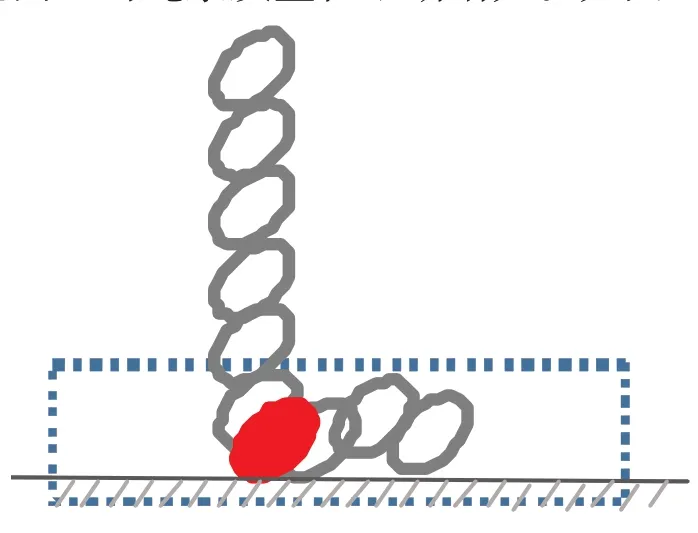
图2 以落地绳索为主体的变质量体系

此时地面上绳索的质量为零，假设已经落地的绳索受到地面的总支持力为N，这里面包含两部分力，一是已经落地绳索的受到地面的支持力，二是正在与地面接触的微元所受到的地面的冲力。代入变质量物体的运动方程，有：

N-σ(L-x)g=σu2，

再将(4)式代入，得此时它对地面的压力，即：

2.1.3 分离问题

将剩在空中的绳索看作“主体”，正在与与地面接触的绳索看作微元，它在分离后的瞬时速度为零，剩余的绳索质量在不断减小，那么这就是“分离问题”。如图3。

图3 以剩余绳索为主体的变质量体系

代入变质量物体的运动方程，有：

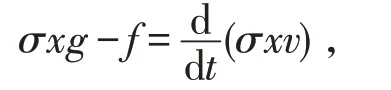
求导数，得：

既可求得此时微元受到地面对它的冲力为：

f=σv2，将两部分力（一是已经落地绳索的受到地面的支持力，二是正在与地面接触的微元所受到的地面的冲力）相加，即得到绳索受到地面的总支持力：

2.2 运用质点动量定理求解

绳索落地问题中，落地处微元所受的冲力还可以用质点动量定理来解决。

以正在与地面接触的微元作为研究对象，并且把它看成一个质点，假设它的质量为dm，初始速度为v，由于地面的冲力作用f，经过Δt时间后速度变为零，忽略空气阻力和它自身的重力，根据质点动量定理，得：

而dm=σvdt，代入，得：

与上面变质量方程得到的结果是一样的。

2.3 两种算法的比较分析

2.3.1 “合并问题”与“分离问题”

把绳索落地问题看作“合并问题”和“分离问题”的相同之处是：首先，不管是“合并”还是“分离”，研究对象都是两个质点构成的质点系，都是变质量问题，所以都可以用变质量物体运动方程求解。其次，绳索空中下落过程都假设为自由落体运动，而且由于绳索是柔软的，所以落地瞬间与地面接触的微元会受到地面给它的一个冲力，不能忽略，并且由于绳索本身的特性，这个力仅仅作用在这个微元上，并不向上传递，这一点不同于刚体。最后，计算过程中，由于剩余在空中的绳索长度为x，而绳索的长度在不断缩短，所以，且，这在两种方法中是相同的。另外，两种解法的不同之处，有以下几个方面：

第一，选取的研究对象不同。

“合并问题”的研究对象是将已经落地的绳索作为“主体”，正在与地面接触的微元与之合并，所以“主体”的质量是不断增大的，即：

“分离问题”的研究对象是将剩余在空中的绳索作为“主体”，正在与地面接触的微元与之分离，所以“主体”的质量是不断减小的，即：

第二，系统的合外力不同。

“合并问题”的系统所受的合外力是有两部分，一是已经落地的绳索所受的重力σ(L-x)g，方向向下，σ(L-x)g＞0，二是地面作用的总支持力N，这里的支持力已经包含了正在与地面接触的微元所受的冲力，方向向上，N＜0。

“分离问题”的系统所受的合外力是也是有两部分，一是剩余在空中的绳索所受的重力σxg，方向向下，σxg＞0，二是正在与地面接触的微元所受的冲力f，方向向上，f＜0。因此，求出的f只是此时地面对绳索支持力的一部分，最后还需加上已经落地部分绳索的重力，即N=f+σ(L-x)g。

第三，运动方程中各部分的速度不同。

“合并”问题中，已经落地的绳索处于静止状态，即主体静止，所以v=0，而微元正在与地面接触，具有速度u2=2g(L+h-x)，也就是它在合并前一刹那的速度。

“分离”问题中，剩余在空中的绳索（主体）正在自由落体运动，它具有速度=2g(L+h-x)，而微元正在与地面接触，由于地面的作用，分离后速度一瞬间静止，所以u=0，也就是它在分离后一刹那的速度。

2.3.2 质点系动量定理与质点动量定理

把正在与地面接触的微元隔离出来，看作质点运用质点动量定理本质上和“合并问题”运用质点系动量定理是相同的。对比式(6)和(9)，将式(6)两边同时乘以dt，有：

式中，σxgdt是剩余绳索在微元落地到速度变为零的时间间隔dt内所受重力的冲量，σxdv是这段时间内它的动量变化量，而另外两项fdt和σvdx就是(9)式中接触地面的微元所受的冲力的冲量和它动量的变化量，从这里也可以看出，此时忽略了微元所受的重力，所以地面对它的冲力就是它所受的合外力，正因为如此，微元正接触还未接触的dt内看作是匀速直线运动，触地后速度突变为零。所以，两种方法得到同样的结果。

3 结语

首先，用理想化的方法建立绳索下落问题的模型，并分析了绳索的柔软和无弹性的条件，得出下落过程中绳索各处的速度相同，与地面接触时地面的作用力只作用在一个点，而不向上传递。然后，分别运用质点系动量定理和质点动量定理进行求解，得到相同的结果，N=σg(3L+2h-3x)，很容易发现，如果绳索起始时刻下端与地面接触，那么h=0，则任意瞬时N=3σg(L-x)，也就是已落地部分所受重力的3 倍，这与已有的研究结果是一致的。最后对这几种方法进行了讨论分析。

由于绳索模型进行了简化处理，所以文章计算的结果与实际情况还存在差异，实际情况要更加复杂，比如绳索本身具有一定的离散性和刚性，与地面之间的作用点并非集中于一点，运动也不完全是平动，还会伴随一定的转动等，许多细节问题还有待进一步深入研究。