单元微分法在拓扑优化中的运用

杨小辉

（广东工业大学机电工程学院，广州 510006）

0 引言

拓扑优化是一种根据给定的负载情况，约束和性能指标，优化给定区域中的材料分布的数学方法。拓扑优化的出现最初只是为了解决一般的机械设计问题。但是，随着对拓扑优化的深入研究，其已被广泛用于许多物理学科，包括固体力学、流体力学、热传导、电磁学等。此外，拓扑优化也已用于许多工程领域，例如运输、建筑设计、复合材料等。

从Bendsøe 和Kikuchi[1]提出均质化方法这一重要的拓扑优化方法到现在，拓扑优化领域已经出现了许多有效可行的方法，如带惩罚的固体各向同性材料（SIMP）方法、演化方法、移动可变形成分（MMC）方法和渐进结构方法（MMA）[2]。

由于FEM几乎可以用于描述所有复杂的工程问题，所以目前大多数关于拓扑优化和拓扑优化方法的研究都是基于有限元结构分析的，只有很少的研究集中在用其他有效的数值求解方法来代替FEM。因此，在这一领域中仍然需要大量的更深入的研究。

最近X.-W.Gao等[3-4]提出一种新的、强形式的数值求解方法，来求解二阶偏微分方程的边值问题。该方法分别借鉴了FEM[5-6]，有限块体法（FBM）[7-8]和无网格法（MFM）[9-10]的部分思想，能快速有效得到稳定解。而且与FEM 相比，EDM具有两个较为显著的特点：（1）不需要任何数学原理或机械原理来构成方程组，因此EDM非常易于编写；（2）无需任何积分。

本文将基于5 节点单元的EDM[11]，运用于基于SIMP 法的拓扑优化[12]，并用MATLAB 进行仿真计算，最后分析讨论其拓扑结果，验证其有效性和准确性。

1 理论基础

1.1 单元微分法

EDM用于解决二阶偏微分方程（PDEs）的边值问题。其关键思想是用节点形函数的一阶、二阶偏导数来表示问题中的相关物理变量，并将问题计算域中的节点分为3类，不同的节点配置不同的平衡方程。具体步骤如下。

（1）用一系列5 节点等参单元划分问题计算域，如图1所示。

（2）推导节点形函数，并得出其一阶、二阶偏导数公式。

（3）用所推导的表达式表示问题中的相关物理变量，如节点坐标，节点位移等。

（4）进行节点分析，并将其分为内部节点、边界节点、界面节点3类，如图2所示。在不同的节点上配置不同的平衡方程（以弹性力学为例）：

①在内部节点配置应力平衡方程：

②在界面节点配置牵引力平衡方程（节点合力为0）：

tij＝ σijηj＝ 0

③在边界节点配置牵引力平衡方程（节点受力平衡）：

tij＝ σijηj＝ ˉt

（5）统计所有节点，进行最终方程的组装，其最终形式为： Ax ＝b ，并对其进行求解，得出结果。

图1 2维5节点四边形等参元素

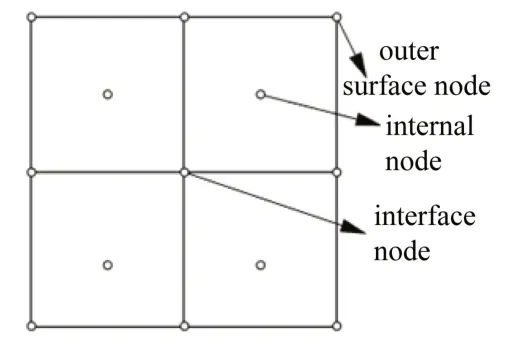
图2 节点的类型

1.2 拓扑优化

本文使用的拓扑优化理论是基于SIMP的结构拓扑优化理论，在SIMP 方法中，引入了相对密度为0～1 的伪可变材料。假设材料的宏观弹性常数与其密度之间存在非线性关系，则介于0～1之间的元素会受到惩罚因子的约束。在一定数量的材料的条件下，找到具有最大刚度（结构的最小柔韧性）的结构材料的最佳分布形式。结构的顺应性被视为目标函数，体积作为约束。则拓扑优化模型如下：

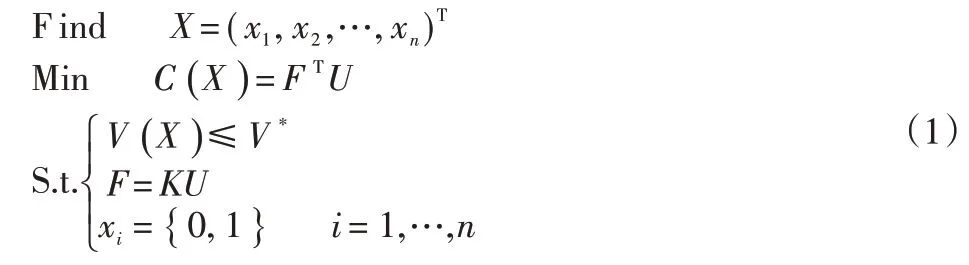
式中：X为单元密度；C( X )为结构顺应性；F为载荷；U为节点位移；V ( X )为结构体积；V*为体积约束；K为整体刚独矩阵。

结构的整体刚度矩阵由单元刚度矩阵组装而成，即：

所以，对于结构顺应性有：

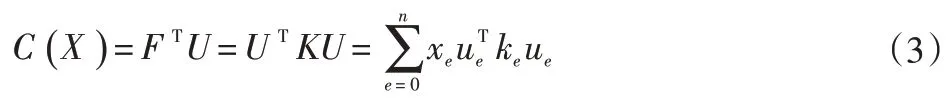
1.3 基于EDM的拓扑优化

将EDM与基于SIMP的结构拓扑优化结合，其目标函数，即结构顺应性可由以下等式表示：

式中：S为结构的受力面积；A为结构的整体系数矩阵；ae为单元的系数矩阵。

所以，拓扑优化目标函数，即结构的顺应性可由如下等式表示：

2 数值案例

2.1 桥梁结构

图3 所示为拱桥模型，长宽比设为4∶1，材料弹性模量E ＝1，泊松系数ν＝ 0.3。约束条件是结构的材料的体积不超过设计区域的体积的30%，以获得满足结构的最小顺应性目的的最佳拓扑结构。计算域网格规模分别为80×20、240×60、320×80、400×100、480×120，并使用MATLAB 进行计算。对于EDM 的，使用上文中介绍的2 种计算方法分别计算结构的顺应性，并与FEM 所得的结果进行比较。最终拓扑结构如图4所示，具体的数值结果如表1 所示。从图中可以看出，基于EDM 的拓扑优化得到的拓扑结构和基于FEM的拓扑优化得到的基本一致。而表中的数据显示，在网格规模较小的时候，前者所需的迭代次数要多于后者，但是当网格规模较大时结果相反。

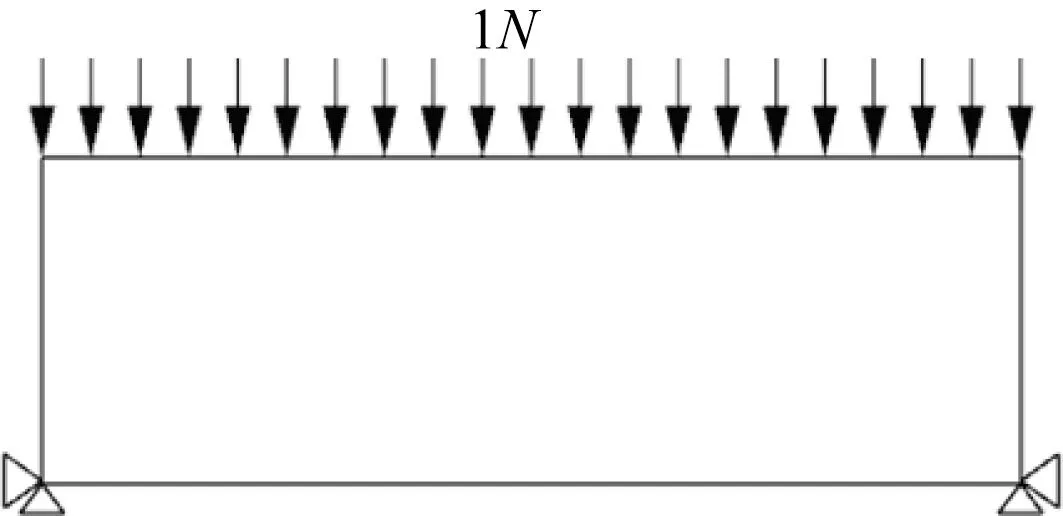
图3 拱桥模型

图4 拱桥最终拓扑结构图

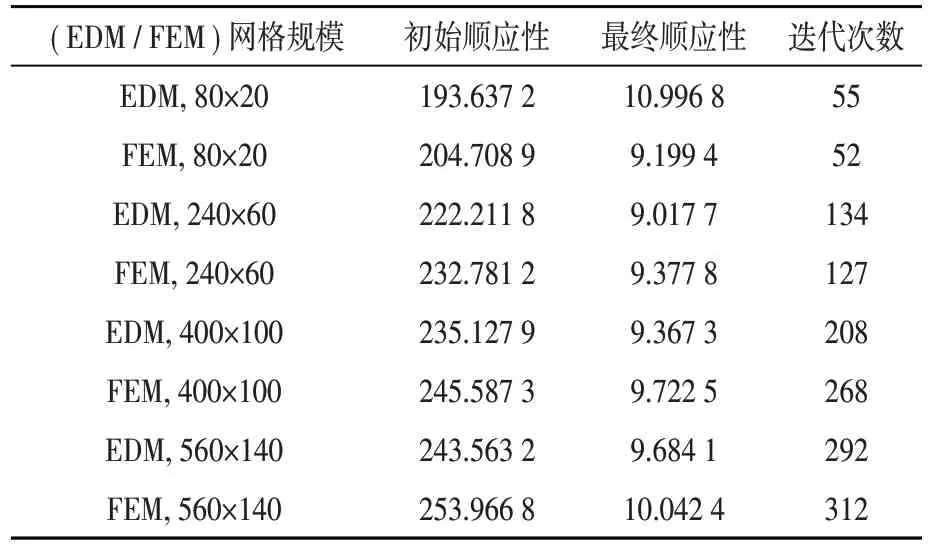
表1 拓扑优化数值结果

2.2 悬臂梁

如图5 所示，用左侧固定的悬臂梁模型简单代表具有矩形立面的高层建筑物，该建筑物在左右两边高度方向上承受水平风荷载。该模型的长宽比为5∶1，材料弹性模量E ＝1，泊松系数ν＝0.3。约束条件是结构材料的体积不超过设计区域的体积的20%，以获得满足结构的最小顺应性目的的最佳拓扑结构。计算网格分别为100×20、200×40、300×60、400×80 和500×100，由MATLAB 计算拓扑结构。在这个案例中下，仅使用EDM（3）进行计算，并将其结果与FEM 计算结果进行比较。最终拓扑结构如图6所示，结果的具体数值如表2所示。

图5 受对称载荷的悬臂梁

图6 悬臂梁最终拓扑结构图

表2 拓扑优化数值结果

从上述结果可以看出，基于EDM的拓扑优化与基于FEM的拓扑优化的拓扑结构基本一致，但是前者所需的迭代次数要少于后者。

以上两个拓扑优化案例证明了EDM的拓扑优化运用上的有效性和准确性，并且案例中基于EDM的拓扑优化所需的迭代次数要普遍少于基于FEM的拓扑优化所需的迭代次数。

3 结束语

本文将基于5 节点单元的EDM 运用于拓扑优化，并通过一系列数值案例进行数值仿真求解与分析。可以得到如下结论：

（1）案例中基于EDM的拓扑优化得到的拓扑结构和基于FEM的拓扑优化得到的基本一致；

（2）案例中基于EDM的拓扑优化所需的迭代次数普遍要少于基于FEM的拓扑优化；

（3）将EDM运用于拓扑优化是可行且有效的。

尽管当前的工作只是以少数的SIMP模型为例，但在将来基于EDM的拓扑优化工作会拓展到其他不同的模型和其他类型的拓扑优化方法中。