凸边坡稳定性分析与优化研究

唐文亮，李卫超，张康财，王 贺

(1.中电建安徽长九新材料股份有限公司，安徽 池州 247100；2.中国水利水电第八工程局有限公司，长沙 410004)

边坡按坡面形状可以分为坡面为平面的“平面边坡”、坡面上陡下缓的“凹边坡”以及坡面上缓下陡的“凸边坡”。文献[1]通过数值模拟软件分析证明了一定情况下存在凸边坡的稳定性优于平面边坡，但没有给出如何确定特定情况下是否存在凸边坡的稳定性优于平面边坡，更没有提出凸边坡的优化设计方法。

瑞典条分法是圆弧滑动边坡稳定系数计算的经典算法，应用较为普遍[1]，为了避免繁杂的分条求和计算和其造成的误差，文献[1-5]分别推导出了瑞典条分法稳定系数的积分表达式，提出了不同的最小稳定系数及最危险滑动面[2]的求解方法，但都是基于坡面为平面的边坡进行的积分，其积分结果对于坡面不是平面的凸边坡已不再适用。

在相同条件下若存在凸边坡的稳定性优于平面边坡，在设计路堑边坡等工程中采用凸边坡的形式[6-9]，既可以提高边坡的稳定性，又可以减少工程量，研究凸边坡有较大的工程价值。针对上述研究存在的不足，本文根据以上积分法的思路，建立了凸边坡稳定性计算的积分表达式，并提出了凸边坡稳定性计算、凸边坡优化设计的方法。

1 凸边坡稳定系数积分表达式推导

凸边坡凸点位置不仅决定了边坡凸面的形态，同时也会影响滑裂面的位置。通常情况下，滑裂面张裂缝位于坡顶平面，但在一定凸面形态下，滑裂面张裂缝会出现在坡面位置，与传统边坡稳定性分析有所区别。所以在分析凸边坡稳定性的时候，应针对滑裂面张裂缝位于坡顶平面和位于坡面两种情况分类讨论。

1.1 张裂缝在坡顶面的圆弧滑动

如图1所示的均质凸边坡，边坡高度为H，边坡体的容重为γ，内摩擦角为φ，黏聚力为c，边坡帮坡角为β，坡面由OA、AB两条线段组成。

因为均质边坡内摩擦角φ>16.7°后，最危险滑动面都通过坡脚[2-3]，最危险滑动面不通过坡脚时的最小稳定系数与过坡脚的稳定系数相差不到2%，所以以坡脚为原点建立图1所示坐标系，假设边坡滑动面为通过坡脚O点的圆弧，圆弧半径为R，圆心为C(xc，yc)，滑动面的上张裂缝为D(L，H)，坡顶点B点坐标为(l，H)，A点坐标为(xa，ya)(xa>0，ya≤H，ya≥xatanβ)。

图1 凸边坡圆弧滑动Fig.1 Arc slip of convex slope

(1)

对于无限小条块defg，设其宽度为dx，高度为h，则

(2)

条块自重dW=γhdx，作用在条块上的抗滑力为：dR=csecαdx+γhtanφcosαdx，下滑力为：dT=γhsinαdx，其中α为圆弧在e点的切线与x轴的夹角，sinα=(x-xc)/R。

边坡的稳定系数F为所有抗滑力与所有下滑力绕圆弧圆心C点的力矩的比值，则

(3)

式中:

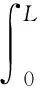
(4)

4LR2-xcyc2-(L-xc)(yc-H)2}/6

(5)

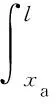
(6)

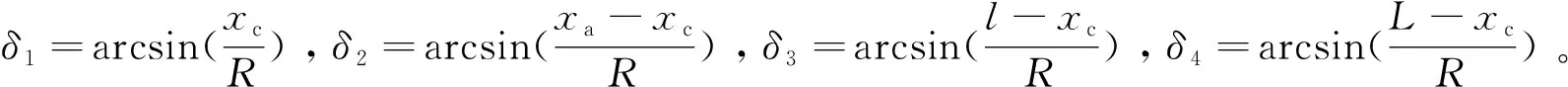
1.2 张裂缝在坡面的圆弧滑动

当k≪tanβ时，滑动面的张裂缝D可能出现在线段AB之间，如图2所示。

图2 上切点在坡面的圆弧滑动Fig.2 Arc slip of the upper cutting points on the slope surface

(7)

式中:

(8)

3xcyc2+3(kxc+b-yc)(xd-xc)(yc-yd)+

Three-component synthesis of 1H-benzo[h][1,2,3]triazolo[4,5-a]acridine derivatives

2(xc-xd)3-2xc3+6R2xd}/6

(9)

(10)

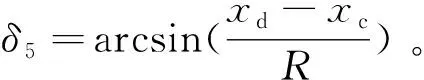
2 凸边坡稳定系数计算与优化设计

2.1 凸边坡稳定系数计算

把式(4)、(5)、(6)带入式(3)，把式(8)、(9)、(10)带入式(7)可知，对于A点确定的凸边坡，其稳定系数F仅为最危险滑面圆心坐标C(xc，yc)的函数，对函数进行求导并令导数为零可得一超越方程组。从理论上可以通过该超越方程组求解，但求该超越方程组无法得其解析解。故此求导方法不适合。

对于滑动面张裂缝D点在坡顶平面的圆弧滑动，如图3所示。根据滑动平衡分析可知圆心应高于边坡[11-12]，即yc≥H，D点横坐标L≥l=Hcotβ，假设D点位置已知，则圆弧圆心应在OD的中垂线CE上，且在DG之上。根据图中几何关系可知：

图3 危险滑动面搜索示意图Fig.3 Searching map for the critical slip surface

(11)

由于假设滑动圆弧通过坡脚O点，危险滑动面的确定简化为危险圆弧圆心的确定，为了避免盲目的计算，需要适当约束圆弧圆心的试算范围[3-4]，使yc≤Hmax，同时约束D点横坐标L≤Lmax，则求解最小稳定系数、确定最危险滑动面即为求解以下约束非线性规划[3-4]问题：

(12)

文中采用迭代法确定最小稳定系数及最危险滑动面。首先赋予L初值l，使yc在取值范围内按一定的步长遍历，由于L、yc确定，xc可由式(11)确定，稳定系数亦可计算，逐点试算取其中最小值即为L=l条件下的稳定系数；再使L在取值范围的按一定的步长递增，求出各步的稳定系数，其中最小值即为最小稳定系数F1m。上述过程计算机编程实现过程见图4。

图4 危险圆弧圆心搜索流程图Fig.4 Flow chart of searching for the critical circle center

图4中的dL、dy分别为L、yc的步长，根据实际情况设定，其值越小计算精度越高但计算耗时越久。式(12)中的Hmax、Lmax需要根据实际情况提前赋值。根据经验，Hmax=3H，Lmax=2l可以快速地求解出结果[4]。若F1m出现在Hmax或Lmax处，则需增大Hmax、Lmax的值，扩大取值区间再次计算。

对于滑面张裂缝D点在坡面的圆弧滑动，如图2所示，可转化为以下约束非线性规划问题进行求解。

(13)

与式(12)相比，式(13)中D点的横坐标的取值范围已经确定，只需根据经验给出yc的上限Hmax即可求解，取Hmax=3H[13]。

求出D点在坡顶平面时最小稳定系数F1m和D点在坡面时的最小稳定系数F2m，两者较小值即为该边坡最小稳定系数Fs，即Fs=min(F1m,F2m)，与Fs对应的圆弧圆心坐标(xs，ys)即为最危险圆弧圆心的坐标，最危险滑动面即可确定。

2.2 凸边坡的优化设计

1)凸边坡稳定性优于平面边坡的验证

在对凸边坡稳定性进行优化设计之前，需保证凸边坡稳定性优于平面边坡，这样才能确保优化工作是有意义的。

当边坡的高度H、边坡体的容重γ、内摩擦角φ、黏聚力c、帮坡角β等参数已知时，利用2.1节的方法可计算给定凸点A(xa，ya)凸边坡的最小稳定系数。当A点置于OB上时，即ya=xatanβ，0≤xa≤l，由式(3)可计算平面边坡稳定性系数Fst。

验证是否存在凸边坡的稳定性优于相应的平面边坡，只需对比Fst,Fsp，若存在Fst>Fsp，则存在凸边坡的稳定性优于平面边坡。

2)凸边坡的优化设计

凸边坡的优化设计即在给定的条件下使设计的凸边坡的最小稳定系数最大，或者使设计的凸边坡在满足一定的最小稳定系数的条件下凸起面积最大，即最大限度减小剥离工程量。对于前者即解决以下约束非线性规划问题，求解方法与式(12)、(13)相同。

(14)

对于后者，即求解式(15)中的约束非线性规划问题。

(15)

式中，Fsd为给定的最小稳定系数，S为△OAB的面积，S=xa(ya-H)/2+ya(l-xa)/2。

3 算例分析

3.1 平面边坡计算

置图1中的A点于线段OB上，令0≤xa≤l，ya=xatanβ，可用式(3)来计算均质平面边坡圆弧滑动的最小稳定系数。

文献[3]中的算例，边坡高度H=50 m，边坡体的容重γ=19.62 kN/m3，内摩擦角φ=11.31°，黏聚力c=58.86 kPa，坡面倾角β分别取17.1°、18.4°、20.0°、21.8°、24.0°，利用式(3)计算边坡的最小安全系数，计算结果与文献[2]中的Bishop法以及瑞典条分法的计算结果相比见图5。

图5 不同坡面角下的最小稳定系数Fig.5 The minimum stability factors under different slope angles

由图5可知，本文积分法的计算结果与瑞典法条分求和求解的结果十分接近，但本文积分法的求解结果一直小于Bishop法，说明本文积分法的求解结果与瑞典法条分求和相比更加准确，但由于计算过程中忽略了分条之间的相互作用力，其计算结果与Bishop相比仍有误差，但平均误差在5%左右。

3.2 凸边坡优化设计

取内摩擦角φ=30°，黏聚力C=15 kPa，重度γ=18 kN/m3，帮坡角β=50°，高度H=15 m的均质边坡。

首先，计算平面边坡的稳定性。令ya=xatanβ，0≤xa≤l，可以求得上述条件下平面边坡的最小稳定系数Fsp=1.096；其次，令xa=0，ya=0，xa、ya均按步长0.1 m在4xa/3≤ya≤10，xa>0的范围内递增，搜索是否存在凸边坡稳定系数Fst>Fsp=1.096。结果在xa=0.2 m，ya=0.3 m时，Fst=1.137>1.096，证明该边坡条件下存在凸边坡的稳定性优于平面边坡。

继续搜索，当xa=1.0 m，ya=2.1 m时，稳定系数取得最大值Fsmax=1.158，相对于平面边坡稳定系数提高了5.65%。采用瑞典条分法和强度折减法，利用边坡分析软件计算上述形态的边坡稳定性系数，结果见表1。

表1 各种方法计算结果对比Table 1 Results obtained by various calculation methods

由表1可知，解析法和瑞典条分法原理相同，但是软件中瑞典条分法采用条分求和逼近方式求解，故造成表中数据差别。强度折减法与前两种方法原理不同，故计算结果差别较大，但同样体现了凸边坡稳定性大于简单边坡的趋势特点。

若要求Fst=Fsp，当xa=1.4 m，ya=4.1 m时，凸起面积S取得最大值Smax=8.375 m2，如果是开挖路堑边坡等工程，假设边坡长度为100 m，则设计成凸边坡最多可以降低837.5 m3的工程量。

4 结论

1)利用积分法代替反复条分求和法，可以大大减小求解稳定系数的工作量的同时提高计算的精度。

2)分析了凸边坡两种可能的破坏形式，给出了凸边坡其稳定性系数和危险滑裂面位置的解析解及求解方法，并基于此给出了凸边坡优化设计的方法。

3)在求解最小稳定系数、确定最危险滑动面的过程中，以xd，ya为设计变量进行试算，可以把搜索范围由一个多边形变为两条线段，便于计算机编程计算，减小计算步骤。

4)凸边坡的优点是一定条件下，相同帮坡角凸形边坡稳定性优于简单边坡。同时，合理应用凸形边坡可有效减小土方工程量。

5)文中假设滑动面通过坡脚，坡面只有一个凸点，对于滑动面不通过坡脚或者坡面更为复杂的边坡，可以利用文中方法重新积分求解。