基于PSD方法的阀门反馈杆随机振动疲劳寿命研究

肖梦凡，杨彬，张立德

（中广核研究院有限公司，深圳 518031）

调节阀阀门反馈杆的作用为反馈阀位给定位器，若反馈杆在阀门运行过程中发生断裂，则定位器输出最小值，影响操作人员对阀门开度的判断。本次研究的阀门为电动调节阀，阀门设计温度为316 ℃，设计压力为94.5 bar（1 bar = 0.1 MPa），阀门在100%开度时，由于管道内流体冲击阀瓣，导致反馈杆与联轴器位置产生随机振动。经现场实测，反馈杆与联轴器位置振动较大，长期运行导致反馈杆连接位置疲劳断裂[1]，断裂后的反馈杆如图1 所示。

图1 反馈杆断裂图Fig.1 Feedback rod break diagram

随机振动理论与方法自1958 年提出后，在各行各业进行了广泛的研究，随着测振技术和有限元仿真技术的飞速发展，使得评估结构在随机振动载荷作用下的寿命成为可能。目前工程上通用的方法为功率谱（PSD）密度法，功率谱密度函数是稳态随机过程的频域描述[2]，表征了随机过程在频域上的能量分布。对于本文研究的反馈杆结构，基于PSD 的随机振动疲劳寿命分析步骤如下：

（1）测量反馈杆断裂位置的随机振动数据，得到时序的振动加速度数据；

（2）通过傅立叶变换，将测量的时序信号转变为功率谱；

（3）利用有限元软件，对反馈杆结构进行PSD分析，得到反馈杆危险结构的局部应力响应；

（4）基于高斯分布和Miner 线性累计损伤准则的三区间法，对反馈杆结构进行随机振动疲劳寿命计 算。

1 功率谱的求解

在工程应用上，常把随机振动视为平稳随机过程，其统计特征量不随时间变化而变化，在求解随机过程的功率谱时，最重要的统计特征量是随机过程 的自相关函数[3]，如式（1）所示，其物理意义在于描述随机过程X ( t )自身在两个不同时刻之间线性依从关系的数字特征：

现推导功率谱的求解过程，定义随时间变换的函数X ( t )为：

定义复变函数X ( ω )为：

A ( ω )和B ( ω )为X ( t )的傅立叶积变换分量，代入并整理可得：

根据欧拉公式可得：

则复变函数X ( ω )可写为：

由于A ( ω )sinωt 和B ( ω )cosωt 均为奇函数，则有：

将上式乘以i 后加到X ( t )上，并不影响X ( t )的值，因此可以得到X ( t )的表达式变为：

将上式各项整理可以得到：

式（2）和式（4）互为傅立叶变换，X ( t )是以时间为变量的函数，X ( ω )是以频率为变量的函数。由于随机过程的自相关函数R ( τ )也是以时间为变量的函数，对其进行傅立叶变换[4]，即可得到随机过程的功率谱密度函数，表达式如下：

式（10）表达的变换对称又被称为维纳-辛欣（Wiener Khintchine）关系式。

由于功率谱密度函数SX( ω )是一个左右对称的双边谱，一般取其正半轴进行研究，即单边功率谱密度GX( ω )。ANSYS 软件也默认采用单边功率谱进行分析。

2 ANSYS随机振动分析理论

在随机振动分析中，可以把反馈杆结构当做线性结构，其动力特性可以在频域内进行描述，如式（11）所示[5]：

其中 [M]——结构非约束自由度的质量矩阵；

[C]——结构的阻尼矩阵；

[K]——结构的刚度矩阵；

{ X }——结构的自由度矩阵；

{ F }——结构受到的激励载荷矩阵。

对于特定的结构，可以通过模态分析获得结构的固有频率及振型，同时也能得到结构的频率响应函数H ( ω )，不同形式的输入功率谱密度（力谱、速度谱、加速度谱等）所对应的响应函数也不相同，针对本文所采用的加速度功率谱，其对应的传递函数如下所示：

式中 ω——激励频率；

ωi——第i 阶模态的自振圆频率；

由于响应过程也可以当做一个随机过程Y ( t )，根据杜哈梅（Duhamel）积分，可求得响应过程与激励过程的表达式，进而可以求得平稳反应过程Y ( t )的自相关函数RY( τ )为：

根据维纳-辛欣公式，平稳反应过程Y ( t )的自功率谱密度为：

由式（14）可以得出，当求得激励的自功率谱后，计算响应的自功率谱变得较为简单。同时，对于零均值的随机过程，当τ = 0 时，可计算反应的均方值：

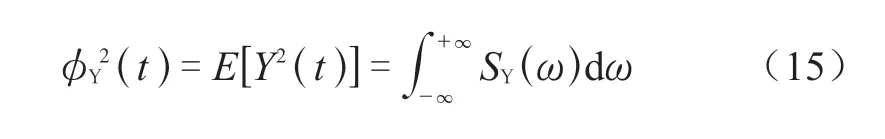
而均方值的开方即为PSD 分析求解的1σ 解，对于结构的危险点，可以求得其不同类型（位移、速度、加速度）的响应PSD。

3 高斯三区间法及Miner线性疲劳累积损伤定律

结构的应力分布时间历程为高斯随机过程，Steinberg 提出的基于高斯分布和Miner 线性疲劳累积损伤准则的三区间法[6]，可以有效求得结构的疲劳寿命。该方法首先将应力分为±1σ，±2σ，±3σ 三个区间，应力幅值落在各个区间的概率如表1 所示。

表1 高斯三区间法Table 1 The Gaussian three interval method

利用Miner 线性累计损伤理论，结构在应力σi的作用下，经历ni次循环的损伤为Di= ni/ Ni，若在k个应力σi的作用下，各经历ni次循环，则定义总损伤为：

当D = 1 时则认为结构疲劳失效，结合高斯三区间法，可得出随机振动总体损伤计算公式为：

式（18）中n1σ、n2σ、n3σ为等于或低于1σ、2σ、3σ 应力水平的实际循环次数，分别等于0.682 7 fμ+T、0.271 8 fμ+T、0.042 8 fμ+T；N1σ、N2σ、N3σ分 别 为1σ、2σ、3σ 应力水平分别对应的可循环次数，由此可以看出，该总体损伤计算公式在结果上是偏保守的。

将式（18）整理可得反馈杆结构在随机振动载荷下的寿命为：

Steinberg 认为超出-3σ ～ 3σ 范围的应力对结构不造成任何损伤，为保守考虑，本文将超出3σ 应力范围的概率考虑到-3σ ～ 3σ 区间范围内，则式（19）可修正为[7]：

4 反馈杆PSD有限元分析

上文已介绍随机振动过程功率谱密度的求解方法和基于高斯三区间法的疲劳寿命计算，利用ANSYS 软件对反馈杆结构进行PSD 分析的流程如图2 所示。

图2 反馈杆随机振动寿命分析流程Fig.2 Feedback rod random vibration life analysis process

采用有限元软件ANSYS Mechanical APDL 14.5建立反馈杆模型如图3 所示，建模采用实体单元Solid186，单元最小尺寸2 mm，共划分26 813 个节点和17 388 个单元。在约束设置方面，与联轴器连接位置由于模拟螺纹连接难度较大，这里做简化处理，模型省略了联轴器内的螺杆，约束主杆面内的螺杆面积节点的自由度，并在此处施加PSD 激励；另一侧螺杆通过一个竖直杆连接反馈杆与万向节，因此在竖直方向上，反馈杆无法产生位移，但其他方向无约束，因此约束此处螺杆竖直方向自由度。

4.1 模态分析

图3 网格划分图Fig.3 Mesh map

进行模态分析是随机振动分析的前提，其目的是为了求得PSD 载荷谱所覆盖的频带内每一阶的固有频率及振型，进而计算反馈杆结构的频率反应函数，即转换函数。对于本文中的反馈杆结构，计算其前三阶固有频率及其三个方向上的参与质量如表2 所示。由表2 可见，第三阶固有频率已达3 450.57 Hz，已超过激励频率2 046 Hz，且前三阶固有频率的参与质量在X，Y，Z 三个方向上均已超90%，这表明采用前三阶模态进行响应分析是足够的。

表2 模态分析结果表Table 2 Modal analysis results

4.2 加速度功率谱

本文所采用的测振工具为COCO-90，测量位置为反馈杆与联轴器的连接位置，测量单位为m/s2，测量总时长为30 s，测量间隔为2.44140625×10-4s，由于数据过于庞大，本文不再列出。得到随机振动时程数据后，可根据第2 节中的原理计算对应的功率谱，计算得到的X，Y，Z 三个方向的功率谱密度如图4 所示。

4.3 随机振动计算结果

在ANSYS 中通过定义矩阵的方式，将所有加速度功率谱导入，并在模型约束节点位置施加图4 中的加速度功率谱，在ANSYS 后处理/POST1 中设置读取第三载荷步的第一子步，即可获得断裂反馈杆的1σ 应力计算结果，如图5 所示。将所有节点的1σ应力进行排序，发现反馈杆最大1σ 应力出现在节点7 448 处，大小为106 MPa，这也是现场实际断裂位置——反馈杆与联轴器连接螺杆的端部。

图4 加速度功率谱Fig.4 Acceleration power spectrum

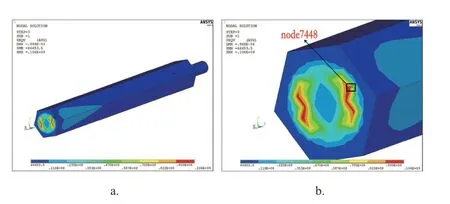
图5 应力计算结果Fig.5 Stress calculation result

选取7 448 节点的X，Y，Z 方向位移分量，计算其PSD 响应作为输出，得到位移响应如图6 所示。

图6 7 448 节点位移响应Fig.6 7 448 node displacement response

由图6 结果可知，7 448 节点的位移响应在低频率段较大，根本原因为反馈杆振动能量集中在低频段，从转谱后的功率密度谱中可以看出功率密度谱值从低频开始呈断崖式下降。同时，7 448 节点的应力响应图也表明反馈杆的应力响应主要来源于低频阶段的随机振动激励，结合模态分析结果可以肯定，低频段随机振动激励过大是导致反馈杆断裂的根本原因。

4.4 疲劳寿命计算

由图5 中的1σ 应力计算结果，结合材料的S-N曲线，并通过式（20）可计算反馈杆的疲劳寿命。反馈杆材料为304L 不锈钢，对应ASME[8]规范中的奥氏体不锈钢材料，其S-N 曲线如图7 所示，图中只给出了部分疲劳强度下对应的可循环次数，1σ、2σ、3σ应力对应的可循环次数需要进行插值计算，插值计算的公式为：

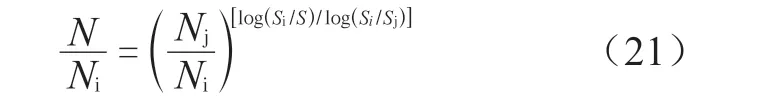
式中Si、S、Sj为应力强度，且Si＞S ＞Sj，将1σ、2σ、3σ 的值分别代入插值公式中，即可得到对应的N1σ、N2σ、N3σ的值。断裂反馈杆的计算寿命如表3 所示。

图7 S-N 曲线Fig.7 S-N curve

表3 寿命计算结果Table 3 Life calculation result

由表3 可知，最终反馈杆的寿命为10.53 h，现场运行记录如表4 所示，反馈杆运行至断裂的时间为15 小时3 分，该误差在寿命计算领域较小，可认为该算法满足要求。

表4 反馈杆运行时间Table 4 Feedback rod operation time

5 结论

本文通过测振工具、理论计算公式和有限元分析方法对电厂断裂的阀门反馈杆进行了一系列的分析，研究了反馈杆断裂失效问题，主要得出以下结论：

（1）通过分析结构应力在随机振动载荷下的动态响应，表明阀门反馈杆断裂主要原因为低频段随机振动激励过大，可通过调整反馈杆结构形式、材料强度等方法提高反馈杆寿命。

（2）利用ANSYS 分析软件结合理论公式所得到的反馈杆随机振动寿命与现场反馈杆实际寿命结果吻合较好，因此利用本文的方法对反馈杆进行随机振动寿命分析是可行的。

现场目前没有对反馈杆随机振动寿命问题分析的方法，本文提供有限元和理论方法相结合的思路，帮助现场解决反馈杆随机振动问题，同时对新型反馈杆的设计提供优化思路，减少设计反复，提高研发效 率。