基于ANSYS的极限载荷分析评定方法与结果讨论

左安达

（惠生工程（中国）有限公司，上海 201210）

基于应力分类法和塑性失效准则的分析设计在压力容器行业中已得到普遍的认可，并解决了很多常规设计无法解决的工程实际问题。但近些年来，在工程应用中发现应力分类法往往存在或保守或冒进的弊端，主要原因在于：应力分类法在对弯曲应力进行划类时，无法进一步区分出一次弯曲应力和二次弯曲应力，如果将其定性为一次应力，则会保守地将二次应力成分划为一次应力，造成保守的设计结构和设计尺寸；相反，则会冒进地将一次应力成分定义为二次应力造成不安全或灾难性的后果[1-2]。分析设计作为一种不断进行技术更新的设计方法，自2002 年以来欧盟EN 13445 标准和美国ASME Ⅷ-2 标准相继推出了基于弹塑性分析的直接法：极限载荷分析法和弹塑性应力分析法。极限载荷分析法在评定准则和结果的准确性方面优于应力分类法，在工程应用的可操作性和效率方面则优于弹塑性分析法。但该法也存在先天性缺点：即只适用于一次加载的工况，而无法考虑多次或循环加载工况下结构安定性的失效模式[3]。基于上述优缺点，极限载荷分析法虽在行业内已逐渐开始得到认可并有所应用，但更多的则是作为弥补应力分类法缺陷的一种辅助验证方法。目前，我国JB 4732 标准修订版中已征求意见并将正式引进极限载荷分析法和弹塑性分析法，同时规定了载荷系数法和塑性垮塌载荷法两种防止塑性垮塌失效模式的评定方法。随着新标准的正式实施以及设计人员对塑性分析法理论知识和有限元软件应用技术的提高，极限载荷分析法势必会在压力容器行业内得到更为广泛的认可和工程应用[4]。

本文基于极限载荷分析的理论基础结合某一实例模型主要探讨其在有限元软件ANSYS 中的实现并针对极限载荷值的确定、评定方法进行结果讨论，以期为极限载荷分析法在行业内的推广应用提供一定的指导价值。

1 设计条件和有限元模型

1.1 设计条件

某高压设备球形封头上开孔接管结构的相关设计参数和材料性能参数分别见表1、表2。

1.2 有限元模型

本计算模型为球形封头上开孔接管的局部模型，不需考虑设备自重、液柱静压力、风载荷、地震载荷及内装物料重量等其他载荷的作用，仅考虑设计压力作用。因模型几何、载荷和材料特性等具有对称性，采用1/2 对称模型建模，选择Solid 185 增强应变单元并划分全六面体网格，单元数量为50 764，网格节点数量为58 653，网格平均质量为76.8%，既能保证求解精度又可提高求解速度（如图1 所示）。

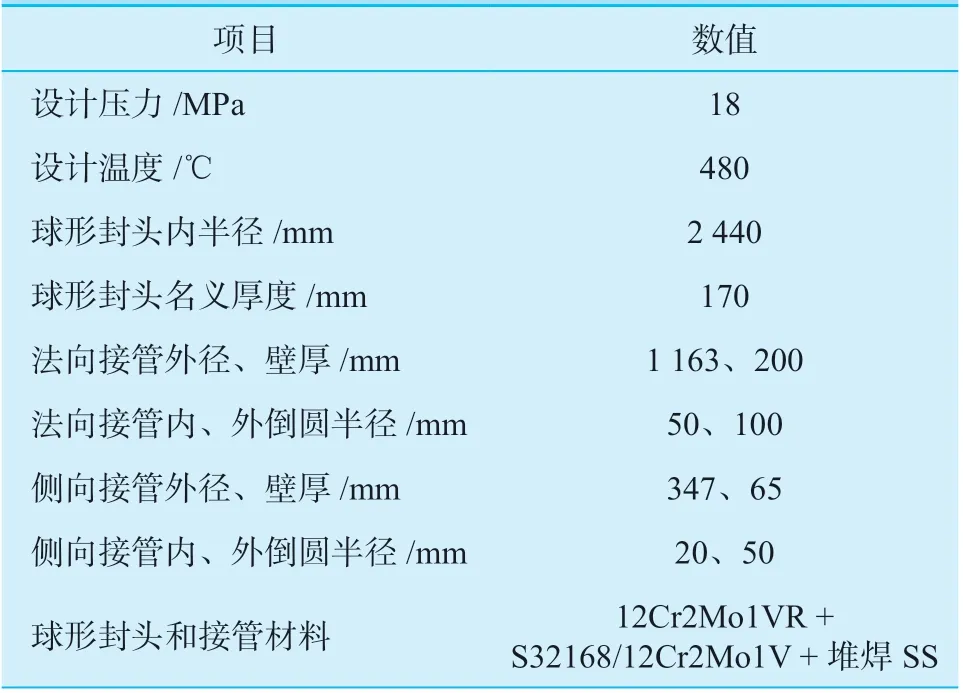
表1 设计参数Table 1 Design parameters and geometric dimensions

极限载荷分析的本构模型一般采用理想弹塑性模型（用于数值计算，如有限元法）或理想刚塑性模型（用于解析求解，忽略弹性变形阶段，只考虑塑性变形阶段，便于简化偏微分方程），两种塑性模型均不考虑材料的应变硬化特性，在理论上求解得到的极限载荷是相同的。本文有限元法采用ANSYS 内置的基于Von-Mises 屈服准则、关联流动准则和小位移理论的双线性等向强化（BISO）模型，将切线模量设置为0 并定义屈服强度为235.8 MPa，以符合极限载荷分析的理论假设和理想弹塑性的数值模型[5]（如图2 所示）。

表2 材料性能参数Table 2 Characteristic parameters of material

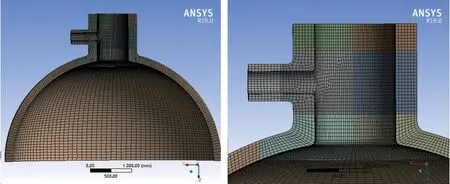
图1 有限元模型和网格划分Fig.1 Finite element model and meshing

有限元模型位移和载荷边界条件：在球形封头下端面施加环向和轴向位移约束，壳体和接管对称面施加对称约束、内表面均施加均布压力，法向和侧向接管端面均施加相应的等效压力[7]。极限载荷分析载荷施加需采用由零到最大值的逐步递增的一次加载方式且载荷增量必须恒正，为获得较为平滑的载荷-位移曲线和更为精确的极限载荷值，需将载荷增量设置的足够小并在进入塑性阶段后进一步减小（可通过ANSYS 中的载荷增量步和自动时间步长等技术来实现）。另外，所有载荷的施加应采用等比例加载的方式[8]（即各种载荷按相同的百分比同时由零增加到最大值）。

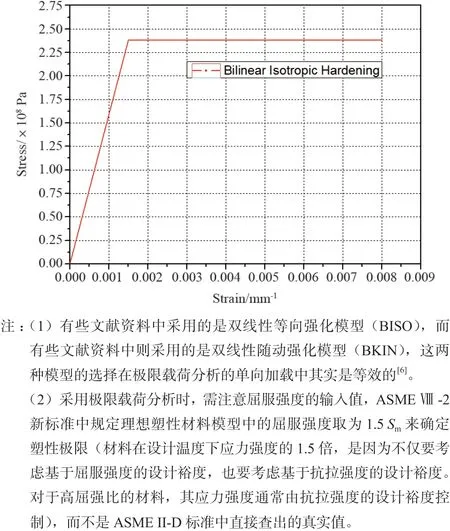
图2 理想弹塑性数值模型Fig.2 Ideal elastic-plastic numerical model

2 极限载荷分析评定方法和结果讨论

2.1 载荷系数法

根据ASME Ⅷ-2 新标准和JB 4732 标准征求意见稿中关于载荷工况的规定，本模型需要按工况1.5 P = 27 MPa（P 为设计压力）的总体准则进行极限载荷分析和评定，以防止结构发生塑性垮塌。合格的评定标准是：若载荷加载到27 MPa 时，有限元计算能够收敛则评定通过，相反则不通过[9]。本文为直观地从应力和应变的角度比较说明和分析，分别进行了4 种载荷工况的计算（0.5P = 9 MPa、1.0 P = 18 MPa、1.5 P = 27 MPa、2.0 P = 36 MPa）。等效应力/应变云图和载荷-位移曲线如图3 所示。

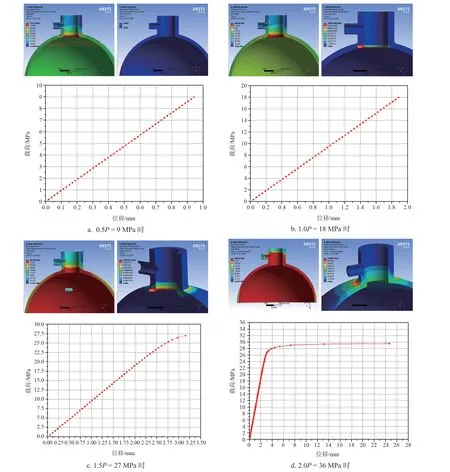
图3 等效应力/应变云图和载荷-位移曲线Fig.3 Curve of equivalent stress-strain and load-displacement

由图3a～d 分析可知：当施加内压为9 MPa 时，结构最大等效应力出现在法向接管根部内表面且值为133.33 MPa，远小于材料屈服强度235.8 MPa，等效塑性应变为0，表明结构此时仍处于弹性变形阶段，并未发生塑性变形。由载荷-位移曲线可明显看出，曲线斜率未发生改变，呈线性增长趋势。当内压增大到18 MPa 时，结构最大等效应力值为240.64 MPa，稍大于材料屈服强度，等效塑性应变为0.000 156 92 mm，表明结构此时已开始进入塑性变形阶段，且接管根部内表面局部微小区域最先屈服，但塑性变形很小。虽然从载荷-位移曲线中看不出明显的斜率变化，但实际上斜率已经开始出现变化，只是变化极其微小，近似与弹性阶段斜率相同。当内压增大到27 MPa 时，结构最大等效应力值为243.89 MPa，等效塑性应变为0.001 617 4 mm，较内压为18 MPa 时增大了近10 倍，此时结构塑性变形由接管根部内表面已经扩展到外表面，整个接管根部较大区域内均已达到屈服极限并进入塑性变形阶段，载荷-位移曲线斜率也已明显出现减小趋势，球形封头内表面应力虽然也比较大，但还未达到屈服强度，因而并未发生塑性变形。在内压为18 MPa 和27 MPa时，最大等效应力值均略超过屈服强度235.8 MPa，理论上计算值是不应该超过屈服强度的，原因在于有限元软件中计算的应力精确值是在高斯积分点上，而云图中显示的则是单元节点上的应力值，该值是由高斯积分点上的应力值通过插值外推到节点上的，因而云图上应力值与屈服强度值会有略微差别。当内压继续增大到36 MPa 时，结构最大等效应力值为252.64 MPa，等效塑性应变为0.903 21 mm，但有限元计算在经过累计120 次迭代后计算结果并不收敛（如图4）。因而，此时计算得到的等效应力和应变值已不具备任何物理意义，且不具备任何参考价值（理论上，达到极限载荷后塑性变形是不可限制的，应力和应变都是不确定 的）。

图4 内压为36 MPa 时有限元计算收敛曲线Fig.4 Convergence curve by finite element calculated at pressure of 36 MPa

图3c 有限元计算结果表明，在内压加载到1.5P=27 MPa 时计算结果是收敛的，因而按载荷系数法对极限载荷分析的评定标准是合格的，即该结构不会发生塑性垮塌。基于计算结果理论分析认为：虽然此时整个接管根部均已达到屈服强度进入塑性变形阶段，但塑性变形仍较小，不足以使接管根部形成塑性铰，故该结构仍具备一定的承载能力而不会发生塑性垮塌。

2.2 塑性垮塌载荷法

塑性垮塌载荷法是基于ASME Ⅷ-2 新标准中关于极限载荷分析的定义而确定的：极限载荷是导致总体结构不稳定的载荷，表现为对小的载荷增量不能求得平衡解（即解不收敛），前文已指出在进入塑性阶段的有限元计算过程中载荷增量需逐步减小，若载荷增量设置得过大，则可能会直接导致计算不收敛，此时不收敛的原因是因为数值发散，并非达到极限载荷值，切勿将数值发散误认为已达到了极限载荷。文献 [8]中介绍了一种判断是否达到极限载荷的数值处理方法，即根据载荷-位移曲线进行判定：若该曲线在趋于水平阶段的斜率小于弹性斜率的1/100，则可判定已达到极限载荷；若该曲线在斜率较大时不能收敛，则属于数值发散。本模型在计算内压2.0P = 36 MPa时设置分析步为1 步，分析步时间为1 s，初始载荷增量步为1×10-2s，最小载荷增量步为5×10-3s，根据上述判定方法并结合图3d 的载荷-位移曲线可判定此时不收敛是因为载荷值已超过极限载荷导致结构发生塑性垮塌而并非数值发散，且计算结果表明在载荷增量步时间为0.822 5 s 时有限元计算结果收敛，但达到0.827 5 s 时计算已不收敛（即发生塑性垮塌），因而可初步判定在上述载荷增量步设置条件的计算精度下极限载荷值介于0.822 5 ～ 0.827 5 s 之间所施加的载荷值（29.61 ～29.79 MPa）。但载荷增量步设置的不同对计算收敛精度有一定的影响，为进一步确定极限载荷值，将初始载荷增量步减小为5×10-3s，最小载荷增量步为2.5×10-3s，有限元计算在经过累计207 次迭代后不收敛（如图5 所示），此时计算结果表明极限载荷值大致介于0.823 75 ～ 0.826 25 s 之间所施加的载荷值（29.655 ～29.745 MPa），结合两个区间范围值，取二者共有的最大值29.745 MPa 确定为极限载荷值。

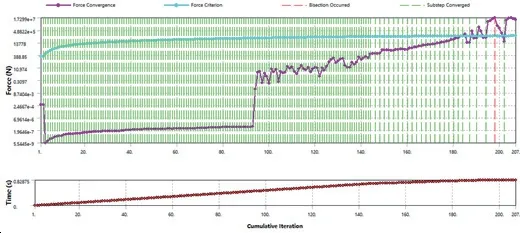
图5 减小载荷增量步后的有限元计算收敛曲线Fig.5 Convergence curve by finite element calculated after the reduced load increment

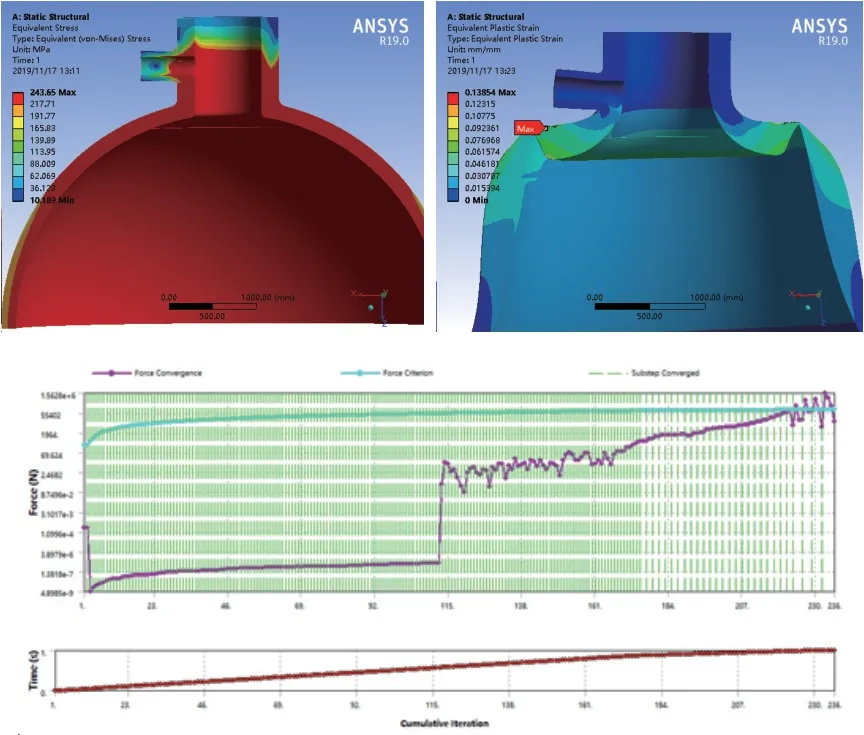
图6 内压为29.745 MPa 等效应力/应变云图和收敛曲线Fig.6 Equivalent stress-strain and convergence curve at pressure of 29.745 MPa

为进一步验证，内压为29.745 MPa 有限元计算结果显示（如图6 所示）：在内压为29.745 MPa 时经过236 次迭代有限元计算结果收敛，最大等效应力值为243.65 MPa，最大等效塑性应变为0.138 54 mm，较内压为27 MPa 时增大了约85 倍，且已从接管根部内表面转移到外表面，充分表明整个接管根部已完全屈服并形成一个塑性铰，进而导致结构发生塑性垮塌（如图6 放大倍数后的应变图）。同时也表明取此值作为极限载荷值是合适的，但此值也并非十分精确的极限载荷值点，真正的极限载荷值可能仍大于29.745 MPa，只是可判断出误差已经极小了。综合上述分析也不难发现，通过有限元数值算法只能判定极限载荷值所在的大致区间，可通过多次减小载荷增量步时间（即增加载荷增量步数）来进一步缩小极限载荷值所在的区间范围，得到更为精确的极限载荷值，进一步缩小误差，只能一步步逼近精确值，而无法十分精确地得出确切的极限载荷值点。但是，减小载荷增量步时间所带来的一个问题是导致求解时间会大大增加，因而在工程应用中需在求解精度和计算效率上做适当平衡。基于本文计算结果，将此结构的极限载荷值确定为29.745 MPa 是偏保守的，且可判断误差已极小，完全满足工程精度要求。

2.3 两倍弹性斜率法

两倍弹性斜率法是ASME Ⅷ-2 老版本标准中确定极限载荷的方法，该法以载荷-位移曲线原点为起始点，作出弹性阶段的弹性斜率直线，然后作另一条直线满足其斜率等于两倍的弹性斜率，该直线与载荷-位移曲线的交点投射到纵坐标上的载荷值即为极限载荷值[10]（如图7 所示）。

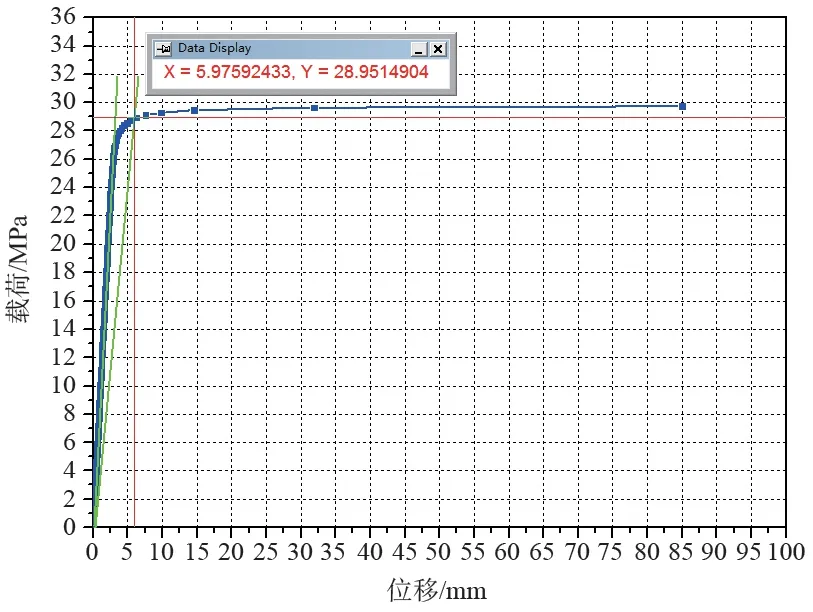
图7 两倍弹性斜率法确定极限载荷值Fig.7 Limit load value confirmed by double elastic slope method

由图7 可知：本模型基于减小载荷增量步后较为精确的载荷-位移曲线并采用两倍弹性斜率法确定的极限载荷值约为28.951 MPa，此方法是一种人为的规定且受人为因素影响较大，所确定的极限载荷值分散性和误差可能会比较大，是真实极限载荷一个保守程度较大的下限近似值。

2.4 双切线相交法

双切线相交法是欧盟标准EN 13445 中确定极限载荷的方法，该法同样基于载荷-位移曲线，分别作出弹性阶段和塑性阶段的切线，两切线相交点投射到纵坐标上的载荷值即为极限载荷值[11]，如图8 所示。

由图8 可知：本模型基于减小载荷增量步后较为精确的载荷-位移曲线并采用双切线相交法确定的极限载荷值约为29.372 MPa，此方法完全由曲线本身决定，相较于两倍弹性斜率法受人为因素影响较小，但问题在于塑性阶段切线斜率不易定准（弹性阶段较为精确），稍有变化便会影响到极限载荷值，同样精度难以保证。

2.5 零曲率法

零曲率法最先由我国清华大学提出，但并未列于我国相关标准中，该法同样基于载荷-位移曲线并考虑材料硬化效应与大变形的影响，提出用载荷-位移曲线的零曲率点来进行极限载荷的确定，指出此点是形成塑性铰并开始显著塑性变形的特征点，能反映出进入显著塑性变形的现象且与该点处的局部性质无关。

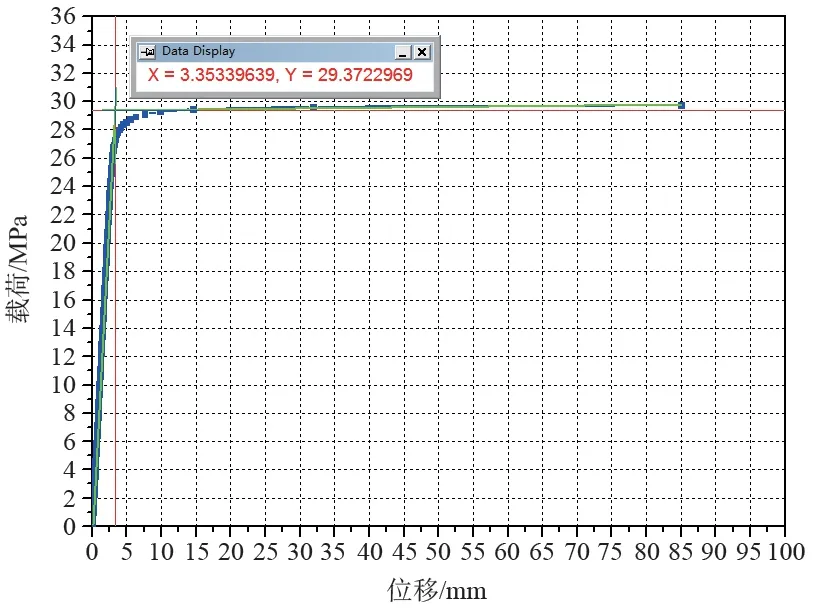
图8 双切线相交法确定极限载荷值Fig.8 Limit load value confirmed by double tangent intersection method

由图9 可知：根据文献 [12]中关于零曲率点的定义，本模型基于减小载荷增量步后较为精确的载荷-位移曲线并采用零曲率法确定的极限载荷值约为29.456 MPa，此方法同样由曲线本身决定且受人为因素影响较小，相较于两倍弹性斜率法和双切线相交法更具有优越性。

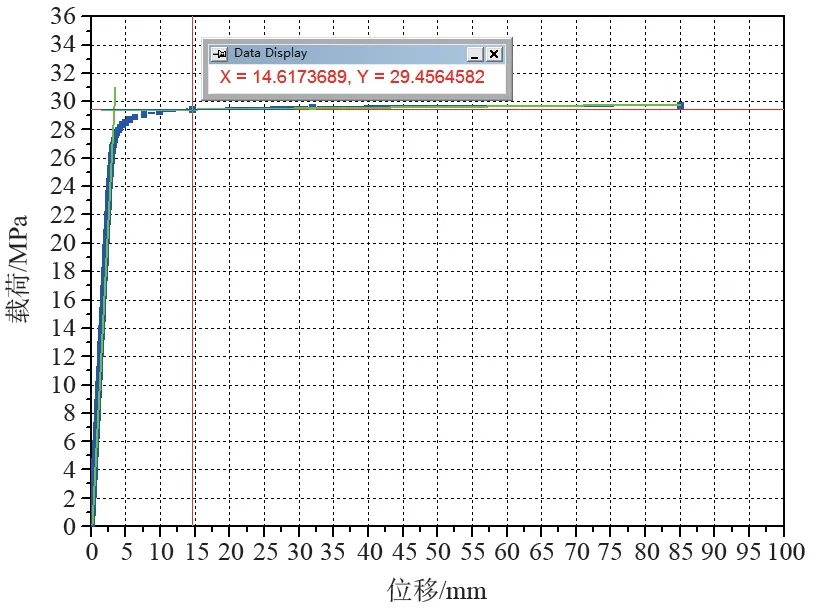
图9 零曲率法确定极限载荷值Fig.9 Limit load value confirmed by zero curvature method

2.6 评定方法的比较和讨论

基于本模型对极限载荷有限元分析进行极限载荷值确认和评定方法的论述可知，各种方法均有其理论基础、评定准则以及优缺点，将其汇总进行对比讨论，如表3 所示。

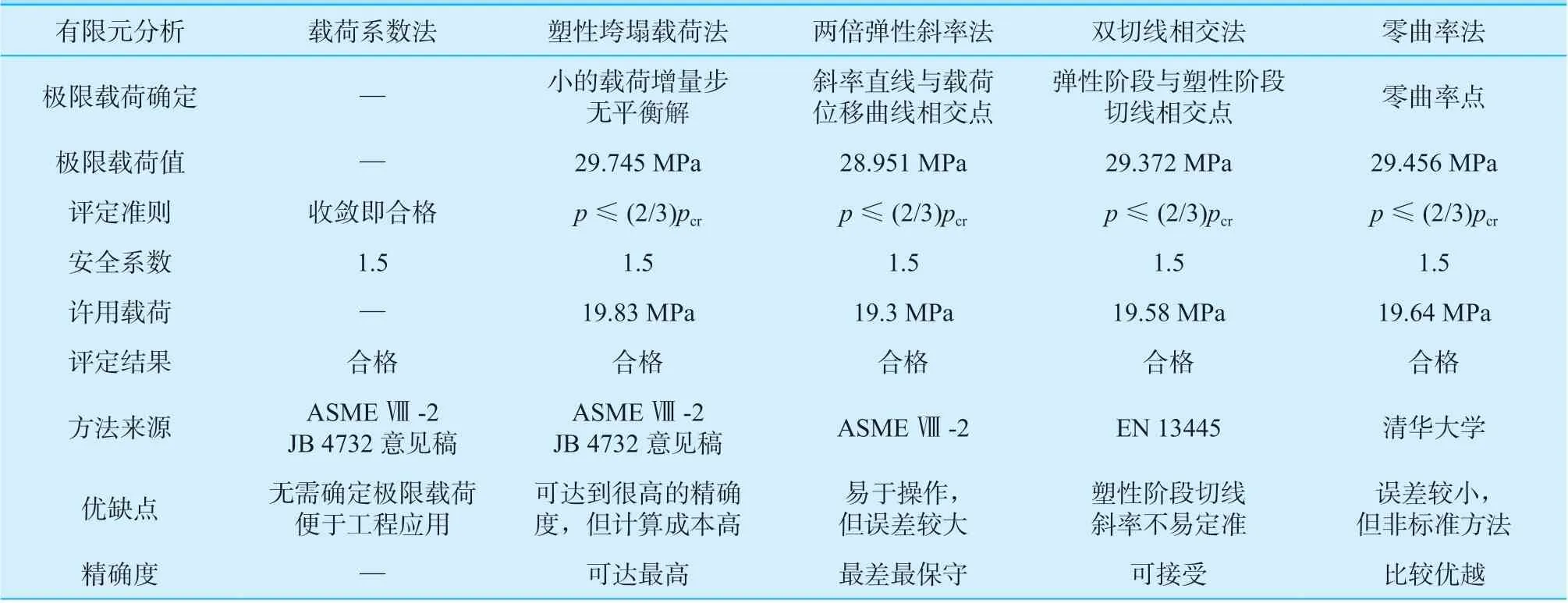
表3 极限载荷分析评定方法对比讨论Table 3 Comparative discussion on the different method of limit load analysis

3 结论

本文基于某一工程实例局部模型，探讨了极限载荷分析在有限元软件ANSYS 中的实现方法，并针对极限载荷值的确定和评定方法进行了对比和讨论，最终得出结论如下[10]：

（1）载荷系数法不需要确定极限载荷值，乘以载荷系数后有限元计算结果收敛即为合格，在工程应用中最易于操作和实现，其余四种方法均需首先确定极限载荷值，然后除以1.5 倍的安全系数确定许用载荷，设计载荷小于等于许用载荷则评定合格。

（2）基于极限载荷定义的塑性垮塌载荷法需直接确定极限载荷值，两倍弹性斜率法、双切线相交法和零曲率法则基于载荷-位移曲线。因而需通过有限元软件进行较为精确的计算，并可直观地通过计算得到的应力、应变云图和载荷-位移曲线对极限载荷进行判断和确定。

（3）有限元非线性计算中，载荷增量步的设置至关重要，若载荷增量步设置得过大，则计算收敛精确很低甚至会数值发散导致不收敛；若设置得过小，则计算时间大大增加。本模型中设置了不同的载荷步求解得到两个极限载荷区间，取两区间内共有值作为极限载荷值，精度可以得到一定的保证，若想确定更为精确的载荷值，则需减小载荷增量步，缩小误差步步逼近精确值，但要耗费很大的计算成本。工程应用中，需平衡求解精度和计算效率，控制误差在工程许可范围内即可。

（4）在极限载荷值确定精度方面，塑性垮塌载荷法精确度可达到最高，零曲率法次之，双切线相交法受塑性阶段切线不易定准的影响在可接受范围内，两倍弹性斜率法易受人为因素影响，精度最差而最为保守。

（5）极限载荷分析在评定准则方面的优越性，弥补了应力分类法无法区分一次弯曲弯曲应力的缺陷，可代替应力分类法中一次应力极限的校核（即Pm≤Sm，PL≤1.5Sm和PL+Pb≤1.5Sm三 个 评定准则），但不能替代一次+二次应力的校核（即PL+Q ≤3Sm），因为极限载荷分析只考虑一次加载的方式，而无法考虑循环加载的安定性失效模式。

（6）随着JB 4732 新标准的修订和正式实施，极限载荷分析的操作和评定方法将在国内标准规范内有据可循，载荷系数法和塑性垮塌载荷法在行业内必定得到进一步的认可和新一轮的广泛应用，但同时对分析设计工程师的理论知识、标准规范的应用和软件操作水平方面提出了更高的要求。