旋转齿筒式水力空化器内空化过程

袁惠新，王赟冰，付双成，周发戚，周龙远，陆健

常州大学机械工程学院江苏省绿色过程装备重点实验室（常州 213164）

在一定温度下，液体中由于局部低压（低于相应温度下该液体的饱和蒸汽压）使液体蒸发而引起的微汽泡爆发性生长的现象被称为空化初生[1]，当液体压力回复时，汽泡群溃灭。这种汽泡群在液体中生长、发展、溃灭及由此发生的一系列物理、化学反应被称为空化。空化泡在溃灭时瞬间产生巨大能量并在流体中形成强射流，泡面射流速度可达100 m/s[2]，可使大分子主链上的碳键断裂，同时破坏微生物细胞壁，使得高分子有机物降解并且使微生物失活。水力空化可以用于强化许多工艺过程及污水处理和生物化工等方面[3-6]，空化技术在食品工业处理方面也有了迅速和更为广泛的发展[7]。空化技术可应用于液态食品的杀菌、混合、均质和乳化等加工过程，朱孟府等[8]研究发现利用水力空化设备可有效去除水中的有机物和微生物，其中大肠杆菌的去除率达99.99%。

常用的水力空化装置主要有孔板和文丘里管两种[9]，此类空化器结构简单，空化强度低，无法满足工业上大规模、高效的处理要求。除此之外，射流管、液哨及齿盘式空化器等新一代水力空化装置尚处于实验室研究阶段且空化强度仍不理想[10-11]。与空化形式单一的静设备相比，旋转齿筒式水力空化器产生空化的机理是由复杂流场中各种力复合而成（以剪切力和离心力为主），摆脱了传统的产生空化方式，可在空化器内产生群空化，空化强度大、空化效率高，因此对空化器空化性能的研究具有重要意义。

采用计算流体力学软件Fluent 19.0模拟齿筒式水力空化器的基本空化性能，以及齿结构参数对空化性能的影响。分析空化器内空化发生机理、流体空化特性，从而对齿筒空化器的进一步探索、优化和应用做出贡献。

1 计算模型、计算方法及边界条件

1.1 计算模型

以在前人基础上改进的旋转齿筒式水力空化器为例研究，并对其结构做了优化[12]。齿筒式空化器主要由静筒和转筒组成，转筒直径160 mm。如图1所示，静筒与转筒同轴，静筒上具有凸出的齿，转筒上具有盲孔，齿孔间形成的空间为物料流动通道，空化则发生在转筒的盲孔内。静筒上的齿和转筒上的盲孔在轴向等距分布有9圈，齿孔轴向对齐，周向等角度分布有20个。静筒上的齿（定齿）与转筒表面有一定间隙（2 mm），形成剪切空间。图1中（a）（b）分别为圆齿静转筒，（c）（d）分别为正方形齿静转筒。其中，方齿横截面与圆齿横截面积相同，圆齿横截面半径为6 mm。

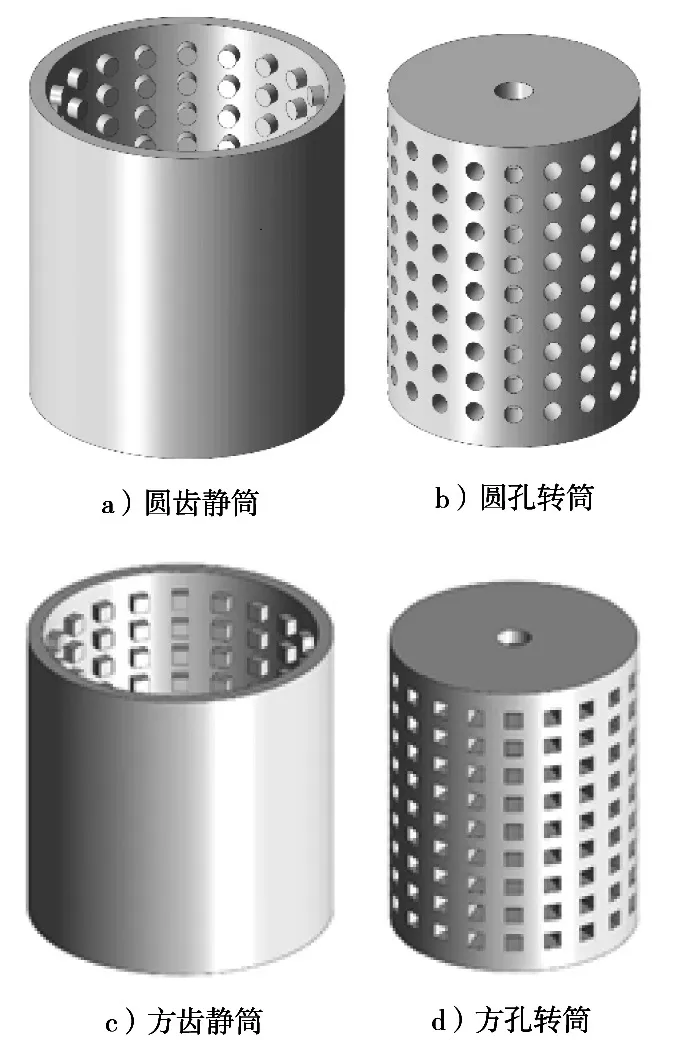
图1 物理模型

采用ANSYS ICEM软件进行网格划分，将流体模型分为4个部分：入口区域、转筒盲孔区域、定齿间区域和出口区域，以interface面进行连接。其中入口区域与出口区域采用结构化网格，转筒盲孔和定间区域采用非结构化网格，网格总数分别为2 416 738（圆齿）和2 439 727（方齿）。生成的流体区域网格如图2所示。

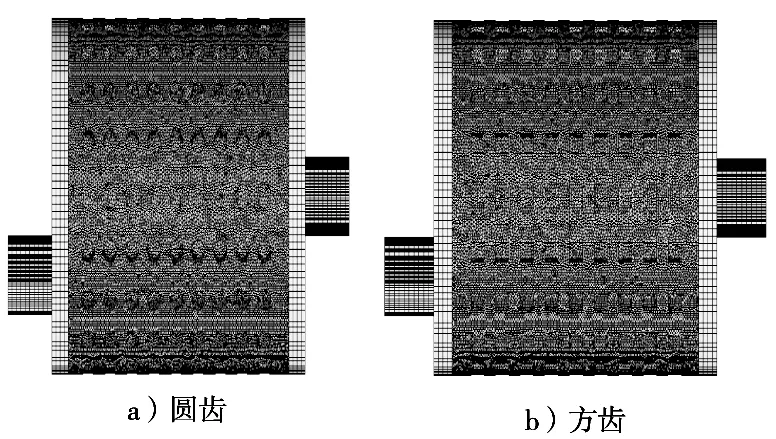
图2 网格划分结果

1.2 计算方法及边界条件

利用计算流体软件ANSYS Fluent进行运算，选用压力基瞬态求解器；选用Mixture多相流模型，不考虑气液两相间的相对运动；采用Realizable k-ε湍流模型，模型可更好地模拟圆孔射流问题；壁面处理采用增强壁面函数；选用Zwart-Gerber-Belamri空化模型，刘厚林等[13]研究表明，在大流量系数下，该空化模型的预测精度更高；压力速度耦合采用PISO算法，其他项均选用具有绝对稳定特性的一阶迎风格式。

Realizable k-ε湍流模型中湍动能及耗散率输运方程为：

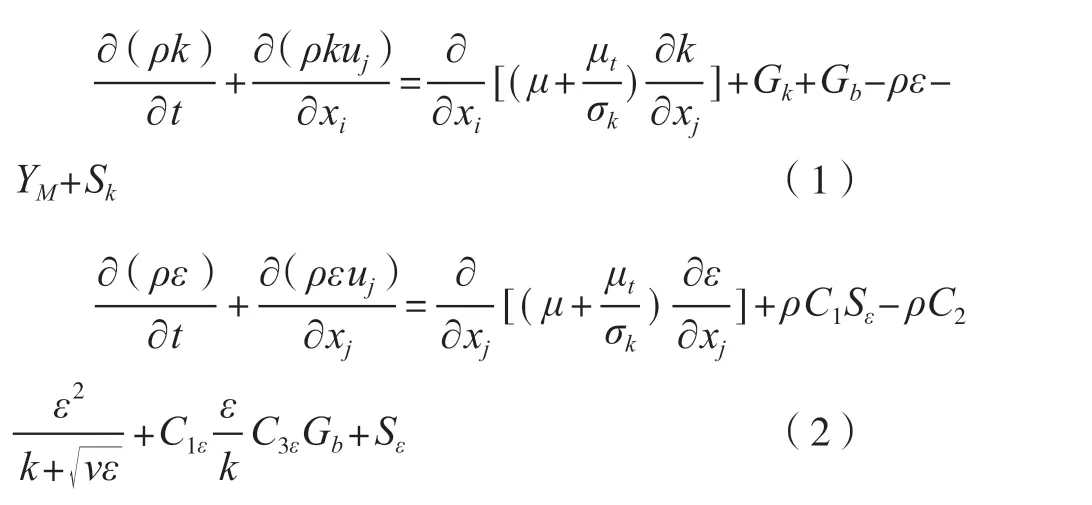
式中：C1=max[0.43η/（η+5）]，η=S×k/ε，Gk由平均速度梯度引起的湍动能产生；Gb由浮力影响引起的湍动能产生；YM为可压缩湍流脉动膨胀对总的耗散率的影响；C1ε、C2ε、C3ε、C2为经验常数，FLUENT中默认值为C1ε=1.44、C2ε=1.92、C3ε=0.09、C2=1.9；σk、σε分别为湍动能和湍动耗散率对应的普朗特数，FLUENT中默认值为σk=1.0、σε=1.3；k和Sε是用户定义的湍动能项和湍流耗散源项。

模拟采用速度入口、压力出口以及无滑移标准壁面函数边界条件。处理量为0.2 m3/h，操作压力为1个大气压。流体介质设置为常温下的水。设置动齿间区域网格为动网格，计算收敛精度为10-5，进行数值模拟。

2 齿筒式空化器的空化机理

齿筒式空化器的空化初生机理主要分为以下两部分。基于伯努利方程的机械剪切力造成的涡空化，流体流经限流区域时，流速增大，压力下降，从而产生空化。定齿与转筒盲孔相对处为限流区域，由于定齿的存在，使得流体流动面积突然变小，从而起到限流作用。经节流后的流体流入转筒盲孔，流体得到释放，压力回复，空泡溃灭。Bernoulli方程：

式中：ρ为液体密度，kg/m3；p为压力，Pa；v为流动速度，m/s。由此可得，液体中的压力p与流速v的关系是流速越大，压力越小，反之亦然。

另一个是由离心力造成的空化。盲孔内液体的受力分析如图3所示（重力在高转速下忽略不计），由于转筒高速旋转，流体受到惯性离心力Fc的作用，液体产生向盲孔外运动的趋势，则在盲孔底部会产生压力损失，使压力降低至低于大气压值，压差随流体向外运动速度的增加而增加，此压差会作用给液体一个压差力Fp方向向内。筒内空化反应稳定时，两力平衡，此时流体不再向外运动，Fc=Fp，即：

即：

式中：ρ为液体密度，kg/m3；V为盲孔内液体体积，m3；r为半径，取盲孔深度的一半到转筒轴线的长度，m；ω为转速，rad/s；p1为盲孔内负压压力，Pa；p2为盲孔外压力，Pa；A为盲孔的横截面积。由式（4）可根据转速计算出盲孔内负压力的值。

图3 盲孔内液体受力分析

3 计算结果与分析

3.1 速度分布

图4是定齿分别为方齿和圆齿的情况下，转速3 000 r/min空化器中流体的相对速度分布图。流体流经限流区域时流体中的气核进入剪切层后被具有较低涡心压力的相干涡结构“吸入”，并生长形成空泡。从图5局部放大图中可看出，液体流入转筒盲孔后在底部形成一个漩涡，这是由于液体进入盲孔后，盲孔内的液体径向速度大，周向速度小，而盲孔外液体由于转筒旋转带有较大的周向速度，因此在盲孔内局部区域形成一个周向速度梯度，进而形成漩涡。随着旋转速度的增加，漩涡中的湍流强度也会增加，这将可能造成瞬态空化的产生，以空化为基础的化学转变只能在瞬态空化条件下才能形成，因此，此漩涡的存在直接影响空化产量及空化器的应用层面。

3.2 压力分布

图6分别为圆齿和方齿时空化器内的压力云图。由伯努利方程可知，在定齿间存在低压区域。由图7可看出定齿间的低压区域主要分布在齿前缘，这是由于转筒转动过程中，转筒盲孔与定齿前缘先接触，此时盲孔内低压流体对定齿间流体会有一个“抽吸”作用，因此对定齿前缘区域造成负压，同时这也使得盲孔内的低压区域向节流点偏移。由于方齿齿间区域较圆齿齿间区域“封闭性”更好，即齿间流体在受到“抽吸”作用而流出后不易有其他区域的流体流入补充其所损失的压力，因此，方形定齿间会有局部负压区域存在，而圆形定齿间则没有。

由离心液压理论公式可知速度与压力呈正比，在盲孔内最外侧会有一个高速液压现象，而低压区域只在靠近旋转中心的盲孔内产生，从图中可以看出，盲孔底部压力值已达到饱和蒸汽压。由于在方孔和圆孔横截面积相同的情况下，方孔周长大于圆孔周长，即剪切长度更长，因此方齿盲孔内的负压区域较圆齿空化器面积更大，空化泡也更容易得到充分发展。

图4 圆齿和方齿z轴截面相对速度云图

图5 圆齿和方齿z轴截面局部放大相对速度云图

图6 圆齿和方齿z轴截面压力云图

图7 圆齿和方齿z轴截面压力云图

3.3 汽相体积分数分布

图8 给出圆齿和方齿时空化器内的汽相分布云图。低压是空化初生的要素之一，结合图5可知，汽相产生区域大致与负压区相对应，方齿空化器内的空化区域略大于圆齿空化器。在流体刚进入空化区时，汽含率（产生的空泡体积占负压区体积的百分比）为20%～30%，流体在负压区内充分发展以后空化率达到95%，甚至100%，由此可知流场中足够的低压段（合适的转子盲孔深度）是确保空化泡集聚能量时间，即空化泡发展时间的重要因素。

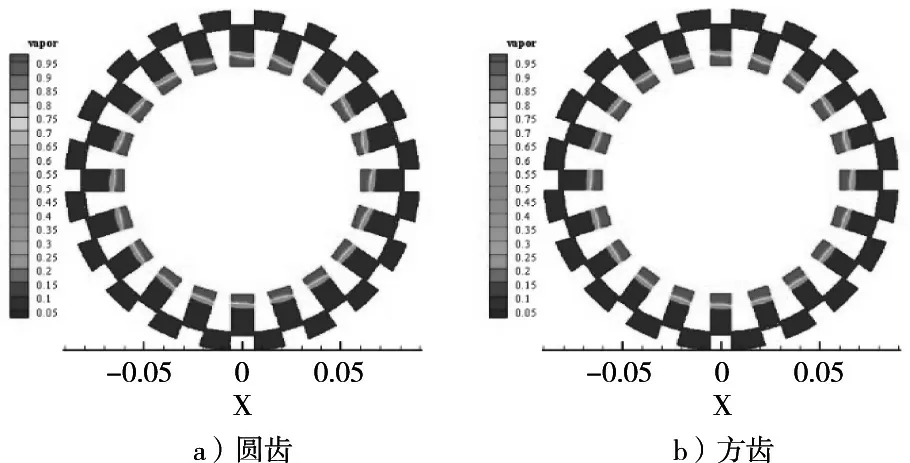
图8 圆齿和方齿z轴截面汽相分布云图

如图9所示，对比2种齿型空化器内的空化泡体积分数占比（空泡相体积分数占流体总体积分数的比值），结果表明，转速为3 000 r/min时，方齿空化器比圆齿空化器空化泡体积分数占比高出14.3%。同时，空化器内初期的空化过程尚未达到稳定，因此在前0.5 s内，会出现空化泡体积分数占比波动较大的情况，此后空化器内空泡产生总量随旋转时间的增加而平稳发展，这说明在齿筒式空化器内的空化过程是一个连续且稳定的过程。在此基础上，分析不同转速下方齿空化器内空化泡体积分数占比随旋转时间的变化规律。如图10所示，随着转速的提高，空化器内局部压力逐渐降低，负压区域占比也随之增大，空化区域面积随转速增大而增大，区域内空化泡体积分数亦随之增大。这说明，适当提高转速更有利于空泡初生，从而可以提高空化效率。基于这一规律，后续可继续考虑增大剪切面积对该齿筒式空化器进行优化研究。

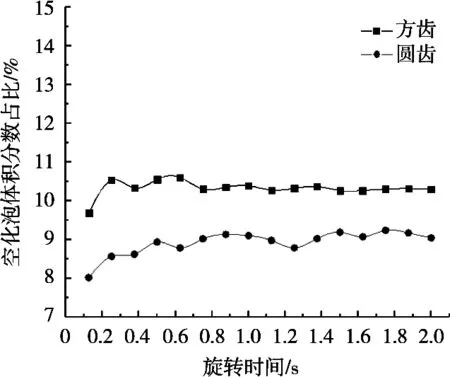
图9 3 000 r/min时方齿和圆齿空化器中空化泡体积分数占比随旋转时间变化曲线

图10 不同转速下方齿空化器中空化泡体积分数占比随旋转时间变化曲线

4 结论

采用数值模拟的方法分析齿筒式水力空化器内的流场，从而研究空化机理。

结果表明：（1）空化器内的空化由离心力和剪切力复合形成。一方面流体经过静齿筒时受到剪切力作用，另一方面，转筒高速旋转，盲孔内液体受到强烈的惯性离心力作用，两种作用力复合，使得空化现象在盲孔内产生。（2）随着转速增大，负压区域随之增大，空化效率更高。（3）改变静、动齿筒上面齿的形状，将圆齿改为方齿，可以增大剪切面积，有利于提高空化率。（4）齿筒式空化器在运行过程中，空化过程连续稳定，与其他现有空化器相比，具有空化区域大、空化率高的优点，并且可以根据需要，增减齿筒长度，达到增减剪切空化次数的目的，在工业应用上更为灵活方便。