Sm原子奇宇称Rydberg态光谱

许照锦张小虎张文纳黄朝宏沈 礼

(天津理工大学理学院，天津 300384)

1 引 言

原子的高激发态研究不仅对原子物理学和天体物理学的发展具有十分重要的意义，而且也有许多实用价值，如激光分离同位素、新型激光器机理的探索以及受控核聚变反应中高温等离子体的诊断等[1-3]。近几十年来，随着激光器及相关技术的进步，碱土金属原子高激发态的研究已取得了十分丰硕的成果[4-9]。

近年来，这方面的研究已转移到能级结构更为复杂的稀土原子上，但研究多集中于Yb、Tm、Eu等稀土原子[10-11]。对于镧系稀土原子这类重元素而言，大多具有未填满的4f次壳层，因可能同时包含最外层电子和4f次壳层电子的跃迁，导致其光谱非常复杂[12-18]。尤其对于Sm原子而言，由于 Sm原子基态4f66s27F0上方存在着4f66s27FJ(J=1～6)这6个亚稳态，当加热Sm金属制备原子样品时，这些亚稳态上也会有布居，从而导致Sm原子的跃迁初态有多种可能。并且Sm原子具有8个价电子，这一特点使得在同一电子组态下会存在非常多的原子状态，所以Sm原子的能级结构极其复杂。总之，Sm原子的这些特点会导致其原子光谱相比于其他稀土原子而言更具有挑战性[19-22]。

目前，Sm原子的高激发态的研究主要集中在偶宇称高激发态[21，23-31]，仅有少量关于奇宇称高激发态的研究[32-33]。这主要是因为Sm原子的基态为偶宇称，对于Sm原子偶宇称高激发态而言，只需要两步共振跃迁；然而奇宇称高激发态需要三步共振跃迁，不确定因素更多，信号探测更加复杂。尤其对于电离阈附近的Sm原子高激发Rydberg态光谱，目前只有偶宇称[23]和同位素154Sm奇宇称[32]的少量研究。

在高激发态光谱的研究中，所采用的电离探测技术一般有光电离[34-35]、场电离[36-37]和自电离[38]。由于光电离属于非共振电离，一般而言，电离光子的能量越接近于高激发态的电离能时电离截面越大。对于电离能只有十几到几百cm-1的高激发Rydberg态而言，若想获得较高的光电离效率，所需电离光的波长远超出染料激光器的波长范围。另外，虽然自电离属于共振电离，但是对于具有复杂能级结构的Sm原子而言，引入自电离光会产生其他不必要的跃迁，而且也会使得实验相当复杂，带来更多的不确定性。当高激发Rydberg态的有效量子数越高时，所需的电离电场强度越弱。特别是对于电离能只有十几到几百cm-1的高激发 Rydberg态原子而言，3 000 V·cm-1的电离电场足以将其电离。所以在接近电离阈的束缚Rydberg态原子更多地采用场电离探测方式。然而，目前尚没有利用场电离探测技术研究Sm原子高激发Rydberg态的报道。

为此，本文结合共振激发和场电离探测技术，对Sm原子在45 200～45 500 cm-1范围内的奇宇称高激发Rydberg态4f66snp(J=1)进行了系统的研究。给出了大量从未报道过的高激发态的光谱数据信息，通过量子亏损分析，得到了3个束缚Rydberg系列，并利用Rydberg-Ritz公式拟合得到了Sm原子第一电离阈的位置。另外，通过不同偏振组合激发，进一步确认了这些Rydberg态的总角动量量子数。

2 实 验

2.1 实验装置

本文所采用的实验装置由激光系统、原子束制备系统和信号采集与分析系统组成，如图1所示。激光系统包括Quanta System公司生产的一台Nd∶YAG固体激光器(型号GNT 0021-0805/L)和3台波长可调谐的染料激光器。其中YAG激光器输出激光的脉冲宽度为6～8 ns，频率为20 Hz，基频光波长为1 064 nm，经过倍频后输出532 nm的脉冲激光，用于泵浦3台染料激光器。通过调谐，3台染料激光器分别输出672.773 nm、684.662 nm和623.500～636.000 nm的激光，线宽为0.1 cm-1。三步激光λ1、λ2和λ3分别通过偏振片和半波片或四分之一波片，确保达到实验所需的偏振状态。因为Sm原子的能级密度非常高，通过改变光程使得三步激光依次延时8 ns进入真空腔，保证Sm原子依次被三步激光激发至选定的Rydberg态从而避免不必要的激发。

图1中虚线圆部分处于真空腔中，包括原子束产生装置、激光与原子相互作用区、离子探测装置(微通道板)。利用机械泵-分子泵组合，真空腔中的压强维持在2.0×10-5Pa以下。通过钽加热丝和温控装置保证原子炉温度在837 K，产生的Sm原子蒸气从原子炉的小孔喷出。喷射出的Sm原子束经过准直后基本与激光束正交，这样可以尽量地避免谱线的Doppler展宽效应。作用区的电场通过在两个距离为1 cm的平行金属板上施加电压实现，金属板中间的栅网既保证了作用区的电场为均匀电场又保证了电离后的Sm+离子可以飞出作用区。在远离微通道板的金属板上通过Avtech公司生产的型号为AVRH-3-B-PN的脉冲电源施加脉冲电压，产生幅值为3 000 V·cm-1的脉冲电场，通过使用AMETEK公司9650型脉冲延时发生器控制脉冲电场与激光λ3之间的延时为0.5 μs，以避免在光与原子作用时由于电场的存在而产生Stark效应。脉冲电场起到电离低于第一电离阈的Rydberg态Sm原子和收集产生的Sm+离子的作用。

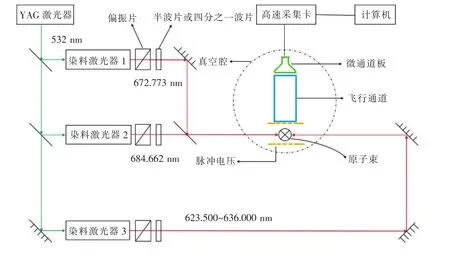
图1 实验装置图Fig.1 Experimental setup diagram

飞出作用区的Sm+离子通过飞行管道自由飞行至高增益(增益约为108)、快响应的微通道板，再利用Agilent Technologies公司生产的高速采集卡(型号U1071A)对经过微通道板放大的信号进行模拟-数字转换，转换后的信号输入计算机，以便进一步分析和处理。

Rydberg态能级位置由文献[39]中4f66s7s7F0态的能量与λ3的光子能量之和确定。其中激光波长使用相干公司的WaveMaster波长计测量得到，精度可以达到0.01 cm-1。另外，我们也对同一光谱进行了多次测量，以便把波长的随机误差减到最小。所以，本实验获得的Rydberg能级不确定度为±0.1 cm-1，这主要是由激光线宽决定的。

2.2 实验原理

在多步共振跃迁中，从基态到高激发态的总的跃迁几率取决于每步光的偏振状态和所有参与跃迁的原子态。在电偶极跃迁中，跃迁几率W1正比于与跃迁有关的Wigner 3J符号模的平方[40]：

其中J1、M1为跃迁初态的总角动量量子数和磁量子数；J2、M2为跃迁末态的总角动量量子数和磁量子数；φ表示光子的磁量子数，激光为线偏振光(π)时，φ =0，为圆偏振(σ±)时 φ = ±1。 对于两步及以上跃迁，总的跃迁几率W等于每步跃迁几率之积。需要注意的是，对于垂直线偏振光(πσ组合)，由于两步光量子化轴的不同，需要将第二步线偏振光分解为右旋和左旋圆偏振光两部分(σ+和σ-)，此时φ1=0而 φ2= ±1。 在零场下，对于总角动量量子数为J的原子态而言能级简并度为2J+1，磁量子数M的取值范围为-J～J。所以总的跃迁几率

其中k表示跃迁的步数，q表示考虑到所有参与到跃迁的能级的简并度以后可能跃迁的数目。如文中所采用的0→1→0→1激发路径，那么两个总角动量为0的能级的简并度为1，两个总角动量量子数为1的能级的简并度为3，所以q的取值为9。对于k=3的三步跃迁而言，存在8种可能的线偏振组合：πππ、ππσ、πσπ、σππ、πσσ、σπσ、σσπ 和 σσσ，考虑到对称性，仅有3种组合πππ、ππσ和πσπ是独立的。同理，圆偏振组合中也仅有σ+σ+σ+、σ+σ+σ-和σ+σ-σ+这3种组合是独立的。当J0=0、J1=1和J2=0时，根据电偶极跃迁选择定则，ΔJ=0，±1(0→0除外)，Rydberg态总角动量量子数J3只能为1。对于这6种偏振组合，三步跃迁总的跃迁几率列在表1中，其中a表示与约化跃迁矩阵元成比例的常数。可以看到，πσπ、σ+σ+σ+和σ+σ+σ-这3种偏振组合下总的跃迁几率为0，即最终不会将原子布局到Rydberg态。而另3种组合下总的跃迁几率相等。

表1 不同偏振组合下的总跃迁几率Tab.1 Total transition probability at different polarization combinations

本文采用三色三光子将Sm原子依次激发至第一电离阈附近的4f66snp Rydberg态。激发路径如图2所示。因为Sm原子基态4f66s27F0与其上方的6个亚稳态4f66s27FJ(J=1～6)的最大能量差仅为4 020.66 cm-1[39]，由于热布居使得基态和这6个亚稳态均有原子布居。为了最大比例地激发Sm原子和保证Rydberg态的总角动量量子数为1，我们选择总角动量量子数0→1→0→1的激发路径。首先，波长为λ1=672.773 nm的激光将处于基态4f66s27F0的Sm原子其中一个6s态电子共振激发到6p态，此时Sm原子处于4f66s6p9F1中间态。然后，波长为λ2=684.662 nm的激光进一步激发该价电子到7s态，此时Sm原子处于4f66s7s7F0态。最后，λ3在623.500～636.000 nm范围内扫描，将 Sm原子激发到4f66snp(J=1)Rydberg态。由于Sm原子能级结构非常复杂，因此上述激光中的两束激光也可能使Sm原子光电离，如λ1和λ3使得Sm原子跃迁到某一束缚态，再通过吸收一个λ3光子电离。在本文中，为了避免这些干扰峰的影响，通过挡住λ1或λ2再扫描λ3从而将其识别出来，以确保所分析的能级都是三步光共同作用下得到的Rydberg态。

图2 激发路径示意图Fig.2 Schematic diagram of excitation

3 结果与讨论

3.1 Rydberg态光谱

πππ偏振组合下得到的Sm原子奇宇称Rydberg态光谱如图3(a)所示，图3(b)为挡住λ2扫描λ3获得的光谱图。在图3(b)中发现的能级只依赖于λ1和λ3，而与λ2无关。这些能级在图3(a)中用*号表示，在分析Rydberg态时需要剔除。另外，挡住λ1扫描λ3没有发现能级。可以看到，整个光谱范围存在有大量的能级，并且随着能量的升高，能级密度逐渐增加，特别是在第一电离阈附近，由于能级间隔小于激光线宽，导致这些能级无法分辨。然而，由于Sm原子能级结构的复杂性，导致光谱中Rydberg能级并不像Eu原子一样可以非常清楚地确定主量子数[37]，这需要进一步地分析量子亏损和能级的演化规律来确定。

图3 Sm原子Rydberg态光谱Fig.3 Spectra of Rydberg states of the Sm atom

3.2 量子亏损和Rydberg系列

根据Rydberg-Ritz公式，有效量子数

其中，RSm=109 736.92 cm-1是Sm原子 Rydberg常数，ERyd是 Rydberg态 Sm原子的能量，I0=45 519.64 cm-1[23]是零场下Sm原子的第一电离阈。

为了进一步确认图3中获得的Rydberg态所归属的系列，将图3中的Rydberg态光谱划分为3个能域分析：45 325～45 400 cm-1、45 428～45 472 cm-1和45 472 ～45 507 cm-1，如图 4(a)～(c)所示。可以看到，在两个较低能域范围内观察到明显的双峰结构，并且两个光谱峰的能量差随着能量的升高而逐渐减小，由于其他干扰能级的影响，导致在有些能域，甚至出现了双峰结构消失的现象。当能量升高至45 472 cm-1以上时，由于两个光谱峰的能量差小于激光线宽，双峰基本上观察不到。随着能量的进一步升高，这些Rydberg能级间隔越来越小，直至45 496.63 cm-1以上，相邻Rydberg能级间隔小于激光线宽，导致它们无法分辨。通过公式(3)可以计算出这些Rydberg能级的有效量子数。由于文献[39]中所报道的奇宇称能级主量子数均小于7，以及文献[32]中奇宇称能级Rydberg电子是f电子，所以本文中得到的Rydberg p电子的主量子数并没有办法完全确定。不过，根据量子亏损δ=n-n*不为负的特点，我们所得到的n与真实的Rydberg能级主量子数会相差1或2。通过双峰结构随着能量升高的演变规律以及同一系列不同主量子数的能级量子亏损近似为常数的特点，可以将这些Rydberg能级分为3个系列，能域范围分别为：45 252.00 ～45 444.24 cm-1、45 243.53 ～45 467.75 cm-1和45 459.54～45 495.62 cm-1。 这3个Rydberg系列所对应的能级位置、主量子数和有效量子数如表2所示。

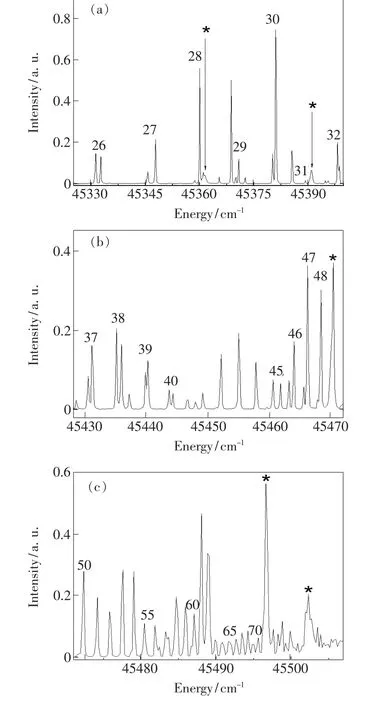
图4 不同能域范围内的Sm原子Rydberg态光谱。(a)45 325 ～45 400 cm-1；(b)45 428 ～45 472 cm-1；(c)45 472 ～45 507 cm-1。Fig.4 Spectra of Rydberg states of the Sm atom in different energy regions.(a)45 325-45 400 cm-1.(b)45 428-45 472 cm-1.(c)45 472-45 507 cm-1.

表2 不同Rydberg系列的能级位置和有效量子数Tab.2 Energy levels and effective quantum numbers of different Rydberg series

表2 (续)

从表2中可以看到，每个Rydberg系列中都有一些Rydberg能级没有出现在光谱中。这主要有以下三点原因：(1)随着能量的升高，双峰间隔逐渐减小以至于小于激光线宽导致无法分辨。这些无法分辨的双峰能级的系列归属，由该能级与哪个Rydberg系列的有效量子数小数部分更接近来确定，如系列1中n=33～35能级没有归属到系列2中。(2)由于其他干扰能级的影响导致Rydberg能级的跃迁强度非常小以至于无法观察到，如系列2中n=42能级。(3)由于挡住λ2扫描λ3仍然存在的能级与Rydberg能级重叠使得Rydberg能级位置无法准确给出，如系列3中n=49能级。

除了这些可以确定Rydberg系列的能级以外，还有一些能级难以归属到其中任何一个系列，这主要是因为Sm原子能级结构非常复杂，这些能级(J=1)的能量位置如表3所示。

表3 不归属于3个Rydberg系列的奇宇称能级Tab.3 Even-parity energy levels that do not belong to any of the three Rydberg series

3.3 跃迁强度

每个Rydberg系列中从4f66s7s7F0中间态跃迁到4f66snp(J=1)Rydberg态的强度随n的变化如图5所示。可以看到，系列1，2中低n值的能级跃迁强度较弱，这主要是因为n值越低，Rydberg能级寿命越短，电离电场相对于光激发延时了0.5 μs，在电离电场作用时，这些低n值的Rydberg态Sm原子大部分已经衰减到其他能级而没有被探测到。当n足够大时，Rydberg能级在没有受到其他能级干扰时，随着n的增加，跃迁强度应该逐渐减小，在3个系列中都观察到这个现象。但是，需要注意的是，有些能级相对于周围的能级，跃迁强度存在突变。这主要是因为基态Sm原子2个或以上的价电子激发后有可能使Sm原子的能量低于第一电离阈，如4f65d6p态，那么这些能级如果处于本文所研究的能域会对束缚Rydberg态产生干扰，甚至出现能级消失的现象。

图5 Rydberg系列跃迁强度的变化Fig.5 Variation in transition intensity of different Rydberg series

3.4 第一电离阈

为了通过Rydberg系列获得Sm原子的第一电离阈，我们利用公式[23]：

其中a、b和c为拟合常数。结合公式(3)和(4)，对3个Rydberg系列拟合结果如图6所示。

图6 不同系列Rydberg能级与n的关系Fig.6 Rydberg levels versus n of different series

各拟合常数和每个Rydberg系列拟合得到的第一电离阈如表4所示。可以看到，每个Rydberg系列拟合得到的第一电离阈基本接近，取平均值45 519.61 cm-1，综合误差为 ±0.79 cm-1，该值与文献[23]中的值(45 519.64±1.39)cm-1非常接近，说明了实验数据的可靠性。

表4 不同Rydberg系列的能级位置和有效量子数Tab.4 Energy levels and effective quantum numbers of different Rydberg series

3.5 偏振光谱

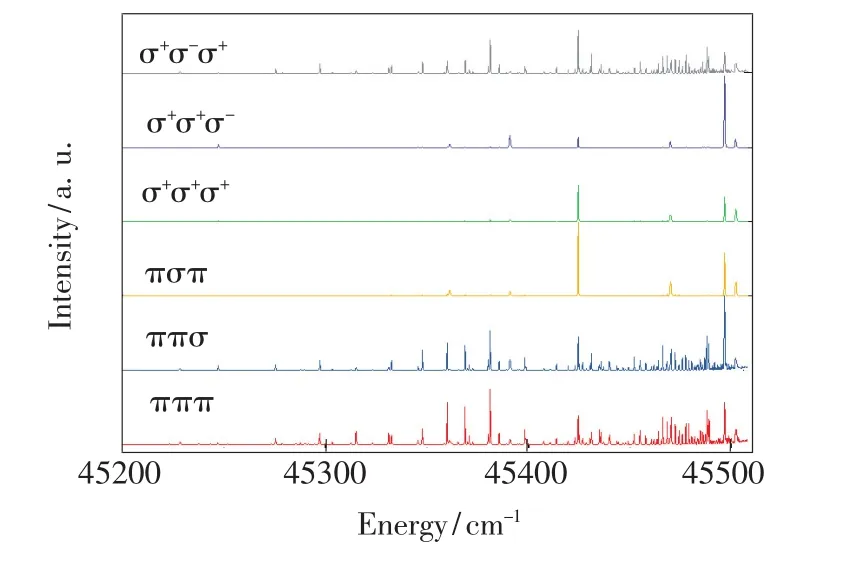
图7 不同偏振组合下的Sm原子Rydberg态光谱Fig.7 Spectra of Rydberg states of the Sm atom with different polarization combinations

如图7所示为在不同偏振组合下的奇宇称Rydberg态 Sm原子光谱。可以看到，在 πσπ、σ+σ+σ+和σ+σ+σ-这3种偏振组合下，光谱图中只存在λ1+λ3所对应的能级，这说明此时总角动量量子数为1的奇宇称Rydberg态是禁戒跃迁。而在另3种组合下，忽略由于激光强度、原子束强度等造成的信号波动，每个能级的跃迁强度基本一致。这些规律都和表1中所列的一致。

4 结 论

本文结合共振激发和场电离探测技术，获得了在45 200～45 500 cm-1能量范围内的Sm原子奇宇称高激发Rydberg态4f66snp(J=1)态光谱，共发现了94个奇宇称Rydberg能级。通过有效量子数和能级的变化规律，确定了3个束缚Rydberg系列，也给出了难以归属到某个Rydberg系列的26个Rydberg态的能级位置。分析了组态相互作用对Rydberg态跃迁的影响，并通过对3个Rydberg系列拟合，获得了Sm原子的电离阈为(45 519.61±0.79)cm-1。除此之外，采用6种偏振组合激发，由偏振选择定则，进一步验证了这些奇宇称Rydberg态总角动量为1。这些结果首次证实了场电离探测技术对Sm原子高激发Rydberg态的适用性，并且通过对奇宇称Rydberg系列拟合得到的Sm原子电离阈与文献中通过偶宇称Rydberg系列获得的值(45 519.64±1.39)cm-1基本一致。