电场和温度对施主中心量子点中束缚极化子基态寿命的影响

乌云其木格连永强李红敏额尔敦朝鲁

(1.内蒙古民族大学数理学院，内蒙古通辽 028043； 2.北京航天万鸿高科技有限公司秦皇岛分公司，河北秦皇岛 066004；3.河北科技师范学院凝聚态物理研究所，河北秦皇岛 066004)

1 引 言

固态量子计算被国内外公认为未来量子信息的发展方向。量子信息的载体可以是任意两态的微观体系，在可选择的多种固态量子计算方案中，以半导体量子点为基本载体的方案最为诱人[1]。不过，要真正实现用半导体量子点载体对量子信息进行存储和处理还有漫长的路要走，许多基本的物理问题尚待解决，譬如本文所关注的半导体量子点信息载体中的消相干问题。这是因为在量子信息中无论是量子的并行运算还是量子模拟，都基于量子态的相干性。然而，半导体量子点信息载体的相干性是不稳定的，极容易受到声子效应的影响，其结果将导致量子相干性的衰减，称为量子比特的退相干。失去了相干性，量子计算的优越性就消失殆尽[2-4]。因此，声子效应导致的退相干问题已经成为半导体量子点载体信息发展中的一个重大障碍。于是，近年来，学术界关于半导体量子点中极化子态衰变的研究日趋活跃。Sun等[5]研究了磁场对抛物势量子点中磁极化子态的跃迁速率的影响。Fotue等[6]研究了氢化杂质束缚极化子态的跃迁速率。Xiao等[7]研究了温度和电场对RbCl抛物势量子点中极化子态的跃迁速率的影响。在考虑存在外磁场时，Sun等[8]研究了温度对RbCl抛物势量子点中极化子态的跃迁速率的影响。Bai等[9]研究了非对称高斯势量子点中LO声子自发辐射率。然而，不难看出，上述关于声子效应对半导体量子点量子比特相干性的影响的研究，仍存在不够充分的方面，亟待完善。首先，上述工作都着眼于用两态极化子激发态的跃迁速率(其倒数被定义为激发态的衰变时间或寿命)来量化量子比特的退相干时间。然而，迄今为止，人们对两态极化子基态的衰变时间或寿命如何影响量子比特的相干性的问题研究甚少。毋庸置疑，这是一个具有同等重要意义的研究课题。因为，对于极化子量子态的相干性而言，无论是其激发态的衰变，还是其基态的衰变，同样都将破坏或衰减量子比特的相干性。其次，上述工作都采用抛物势描述量子点中电子的限定势。其实，抛物势是一种过于简化的模型。一些实验结果证实真实的限定势应是非抛物形的阱状势[10]，如密度矩阵势或非对称三角势、高斯函数限定势等，其中高斯函数限定势阱是一个很好的近似[11]。再次，近年来，引入高斯限定势阱研究低维结构电子态的性质在量子阱结构中已有不少出色的工作报道[12-15]，但是，相关研究在量子点结构领域甚少，尤其是研究电场下施主中心量子点中束缚极化子态衰变的工作尚未报道。本工作将填补该领域的某些研究空白。

迄今为止，已有一些研究极化子基态寿命方面的实验工作[16-17]和理论工作[18-20]报道，结果表明，研究极化子态的衰变不仅具有基础理论意义，也具有重要的应用前景。本文通过对非对称高斯势施主中心量子点中束缚极化子基态寿命的研究，进一步完善了声子及其关联效应导致量子点量子比特退相干的内涵。

2 理论模型与方法

施主中心量子点体系由一个电子和位于量子点中心的一个带正电的施主杂质构成。这里我们考虑电子同时受到量子点局域限定势和施主杂质库伦势作用，并与介质中体纵光学(LO)声子场相互作用。用非对称高斯限定势VG(z)和抛物限定势VP(x，y)分别描写电子在沿量子点生长方向(z轴方向)及其垂直方向(O-xy平面)的受限。施加沿z轴方向的电场F，则电场-施主杂质-电子-LO声子场四体相互作用体系的哈密顿量可以写成[9]：

其中

VC(r)=-e2/(ε∞r)表示电子与施主杂质间的库伦作用能。mb是电子的带质量，r和p分别表示电子的空间位矢和动量，ω0为抛物势受限强度，V0表示非对称高斯限定势阱的阱深且V0＞0，L表示其阱宽，亦称量子点的有效厚度。公式(1)中其他物理量的意义与文献[9]相同。

其中

是Lee-Low-Pines幺正变换[21]，其中fk(f*k)为变分参数。依据Pekar类型的变分法[22]，体系的基态和激发态试探波函数分别选为

其中，λ0和λ1为变分参数，是LO声子的真空态，由=0确定。 将公式(1)、(3)～(5)分别代入公式(2)中，可确定变分参数 fk、λ0和λ1。利用这些变分参数并经冗长计算，可分别得到束缚极化子基态的声子平均数N0及激发态与基态能隙ΔE=E1-E0：

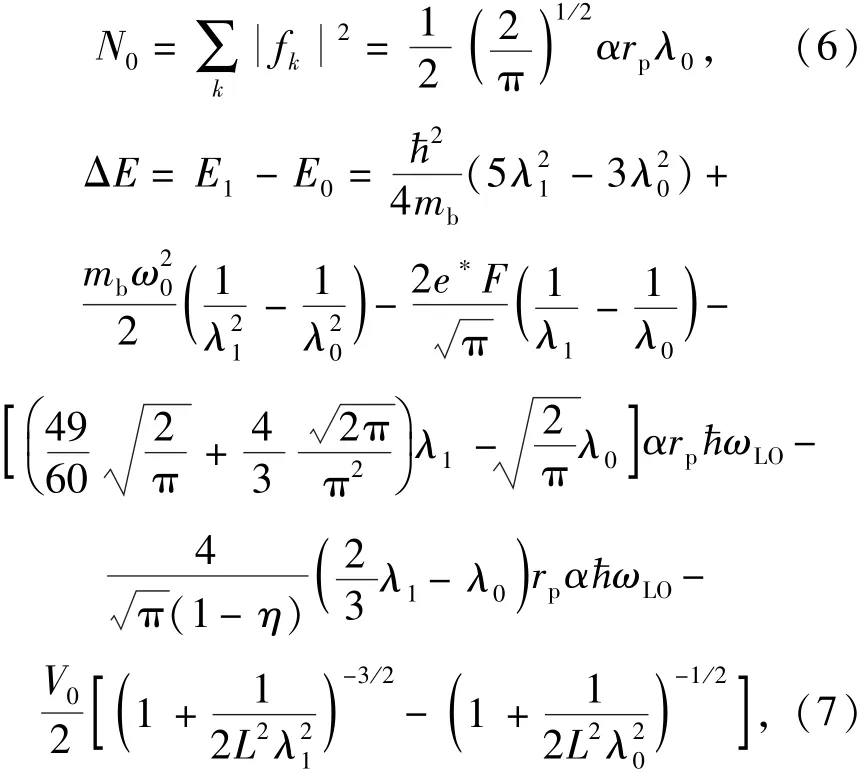
其中，α为介质的电声耦合常数，η=ε∞/ε0为介质的介电常数比称为极化子的有效半径。由于电子-声子相互作用和温度的影响，量子系统中会发生量子跃迁。根据费米金定律，可以得到电子吸收一个LO声子后从基态到激发态的跃迁几率，跃迁速率为[19-20]：

其中，τ0为极化子基态寿命，N0为基态LO声子数。在有限温度下，电子-声子体系不完全处于基态，晶格热振动不但激发实声子，同时也使电子受到激发，极化子的性质是由电子-声子体系对各种可能状态的统计平均值描述[23]。根据量子统计理论，公式(8)中N0可由LO声子数统计平均值代替：

其中，T为绝对温度，γ=ħωLO/(kBT)称为温度参数，kB为玻尔兹曼常数。

3 结果与讨论

图1～11分别给出了非对称高斯势量子点中施主中心束缚极化子基态LO声子平均数N0、基态与激发态的能隙ΔE=E1-E0和吸收一个LO声子后从基态到激发态的跃迁速率的数据曲线。

图1描绘了束缚极化子基态LO声子平均数N0在不同温度系数γ下随电声耦合常数α的变化。由图1可以看出，声子平均数N0随电声耦合常数α的增加而增多，这是因为随着α的增加，电声相互作用增强，导致电子周围聚集更多的声子。由图1还可以看出，当α取定值时，N0随γ的增加而减少，换言之，基态LO声子平均数N0随温度T的升高而增多。这是因为晶格热振动随温度的升高而增大，致使电子周围声子数量随温度的升高而增多。

图1 声子平均数N0在不同温度参数γ下随电声耦合常数α的变化Fig.1 Mean number N0of phonons as a function of the electron-phonon coupling(EPC)constant α at different temperature parameter γ

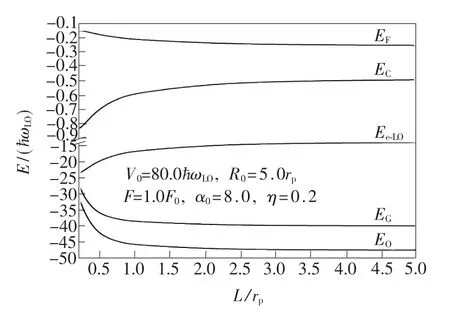
图2 束缚极化子基态能量E0及其各组成部分随高斯势阱宽L的变化Fig.2 Ground state energy E0of the bound polaron and its components versus the well width L of the asymmetric Gaussian(AG)potential

图2 表示了束缚极化子基态能量E0及其组成部分随高斯势阱宽L的变化。由图2可以看出，E0＜0，即极化子处于束缚态，这是因为E0的组成部分对E0的贡献都为负。由图2还可以看出，能量随L的减小而减小。但是E0的各组成部分随阱宽L的变化有所不同，分别解释如下：电子-LO声子耦合能的绝对值随L的减小而增大，是因为量子点中电子-声子耦合能由于粒子纵向(z轴方向)运动空间L被压缩而增大；电子在施主杂质电场中的库伦能的绝对值随L的减小而增大，这是因为随L的减小，电子与施主中心的距离缩短，致使库伦能的绝对值变大；电场引起的附加能量的绝对值随L的减小而减小，这主要是随L的减小，施主中心对电场的屏蔽作用增大，致使随L的减小而减小；高斯势能的绝对值随L的减小而减小，这是因为随L的减小而减小。

图3表示束缚极化子基态与激发态的能隙ΔE在高斯势不同阱深V0下随其阱宽L的变化。由图3可以看出，ΔE随L的变化规律在L的不同取值区间有所不同，呈现出一非对称“高斯分布”的特点。这是由量子点的厚度变化引起的声子效应的具体表现。首先，当L较大时，ΔE随L的减小而增大至(在L0点)一最大值。这是因为，束缚极化子的基态能量E0和激发态能量E1都是负的，且另外，量子点中电子的动能和电子-LO声子耦合能由于粒子纵向(z轴方向)运动空间L被压缩而增大，导致极化子能量的绝对值增大，其中，基态能量随L的减小而增大的幅度大于激发态能量增大的幅度，致使能隙ΔE=E1-E0随L的减小而增大。其次，当L=L0时，ΔE的取值达到最大值，这意味着由量子点厚度的变化引起的LO声子效应达到峰值。再次，当L＜L0时，ΔE从峰值开始随L的减小而迅速减小。这是因为当量子点的有效厚度L非常薄时，因其内LO声子数迅速减少，致使电子-LO声子耦合能的贡献迅速减小。从图3还可以看出，当L取一定值时，能隙ΔE随高斯势阱深V0的增加而增大。这是因为高斯势能VG(z)=-V0exp(z2/2L2)＜0且随V0的增加而增大，致使束缚极化子能量的绝对值随V0增加而增大。而且，基态能量随V0的增加而增大的幅度大于激发态能量增大的幅度，导致能隙ΔE随V0的增加而增大。

图4描绘了能隙ΔE在不同介电常数比η下随高斯势阱宽L的变化。由图4可以看出，ΔE随η的增加而增大。这是因为施主中心杂质电场中电子的库伦势VC∝-1/(1-η)随η的增加而减小，使得对极化子能量的贡献随η的增加而增大。而且，体系基态能量随η的增加而增大的幅度大于激发态能量增大的幅度，致使能隙ΔE随η的增加而增大。

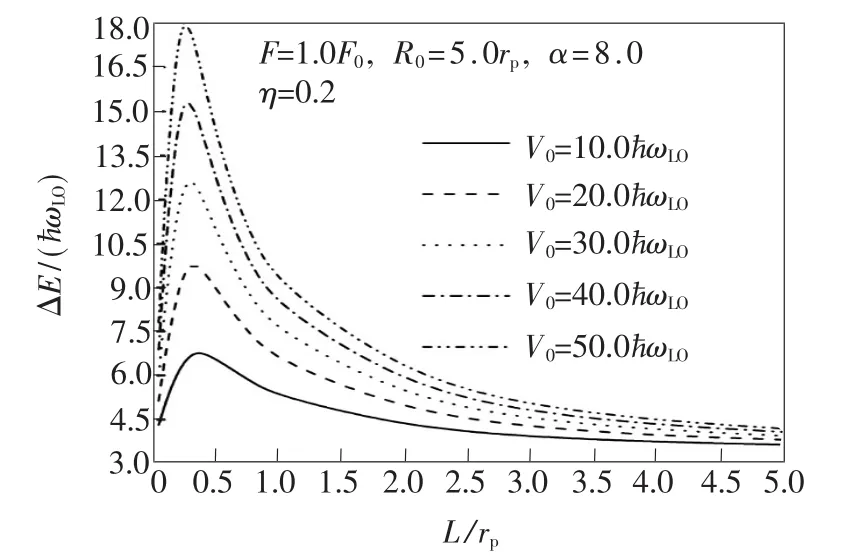
图3 能隙ΔE在非对称高斯势不同阱深V0下随其阱宽的变化Fig.3 Energy gap ΔE versus the well width L under different well depth V0of the AG potential

图4 能隙ΔE在不同介电常数比η下随高斯势阱宽L的变化Fig.4 Energy gap ΔE versus the well width L of the AG potential under different dielectric constant(DC)ratio η

图5 表示能隙ΔE在不同电声耦合常数α下随非对称高斯势阱深V0的变化。由图5可以看出，在阱深V0给定时，能隙ΔE随α的增加而增大。这是因为电声耦合常数α越大，意味着电声耦合越强。其中，激发态电声耦合比基态电声耦合强度弱，所以能隙ΔE随耦合强度α的增大而增大。

图5 能隙ΔE在不同电声耦合常数α下随非对称高斯势阱深V0的变化Fig.5 Energy gap ΔE versus the well depth V0of the AG potential under different EPC constant α

图6 能隙ΔE在不同电场强度F下随抛物势范围R0的变化Fig.6 Energy gap ΔE as a function of the range R0of the parabolic potential under different electric field F

图7 束缚极化子基态跃迁速率在高斯势不同阱深V0下随其阱宽L的变化Fig.7 Ground-state transition rateof the bound polaron as a function of the well width L at different well depth V0of the AG potential

图8 基态跃迁速率在不同电声耦合常数α下随高斯势阱宽L的变化Fig.8 Ground-state transition rateas a function of the well width L of the AG potential at different EPC constant α

图9 基态跃迁速率在不同电声耦合常数α下随温度参数γ的变化Fig.9 Ground-state transition rate as a function of the temperature parameter γ at different EPC constant α

图10 基态跃迁速率在不同介电常数比η下随高斯势阱宽L的变化Fig.10 Ground-state transition rateas a function of the well width L of the AG potential at different DC ratio η

图11 基态跃迁速率在不同电场强度F下随抛物势范围R0的变化Fig.11 Ground-state transition rate as a function of the range R0of the parabolic potential at different electric field F

图11 表示基态跃迁速率τ-10在不同电场强度F下随抛物势范围R0的变化。由图11可以看出，随R0的减小而减小，即基态寿命τ0随抛物势范围R0的减小而增大。这一结果与文献[19]的抛物势结论一致。根据图6，这是因为能隙ΔE随R0的减小而增大，致使寿命τ0随R0的减小而增大。比较图11和图7可以看出，抛物势和非对称高斯势对量子点中极化子基态寿命的影响明显不同，这种不同既反映了电子在量子点生长方向及其垂直方向的不同受限对寿命τ0的不同影响，也反映了量子点厚度对寿命τ0的特殊影响。由图11还可以看出，随F的增加而增大，即基态寿命τ0随电场强度F的增加而缩短，这一结果与文献[20]的结论一致。这是因为能隙ΔE随F的增大而减小，导致寿命τ0随电场F的增大而缩短。这意味着施加电场将对量子点量子比特相干性造成干扰。

4 结 论

研究了外电场、温度、材料的介电常数比和电声耦合常数等对非对称高斯势施主中心量子点中束缚极化子基态寿命的影响。数值结果表明：(1)量子点约束势的高度和宽度对极化子基态寿命的影响较大，即束缚极化子基态寿命随非对称高斯势阱深的增加而增大，随非对称高斯势阱宽的变化呈非对称“高斯分布”特点。(2)束缚极化子基态寿命随材料的介电常数比的增加而增大、随电声耦合常数的增加而缩短、随环境温度的升高而减小、随电场强度的增加而缩短。(3)环境温度、施加电场和声子效应都将干扰量子点量子比特的相干性。