一类甘油生物歧化为1,3-丙二醇过程的最优控制

赵宇佳, 徐恭贤

(渤海大学 数理学院, 辽宁 锦州 121013)

1,3-丙二醇是一种十分重要的化工原料,它可用于合成各种药物,例如,新型聚酯PTT和新型抗氧化剂.此外,在合成洗涤剂、增塑剂、防腐剂、乳化剂等领域也有广泛应用[1-2].近些年来,微生物发酵法生产1,3-丙二醇的研究受到了国内外众多学者的广泛关注[3-19].例如,Frazão[4]等构造了葡萄糖发酵生产1,3-丙二醇的生物合成路径.Yuan等[5]研究了甘油间歇发酵过程的鲁棒参数辨识.Xu等[6]研究了甘油连续发酵过程的多目标优化.谭雯心[7]建立了参数辨识动态优化模型,基于B样条法和吉洪诺夫正则化法估计出多种代谢物浓度的实验值导数,使得误差值降低,从而得出原参数辨识问题的最优解.孙亚琴[8]通过对微生物转化等过程进行模拟分析,建立了酶催化与基因调控非线性动力学方程.王丹等[9-10]研究了一类甘油流加过量动力学系统的动态优化,但是论文作者没有考虑甘油生物歧化过程中的还原途径酶催化作用.因此,本文结合甘油生物歧化为1,3-丙二醇过程的非线性动力系统,建立了其还原途径酶催化过程的最优控制模型,并通过有限元配置法求其最优解,为将来的生物过程优化研究提供指导.

1 数学模型

考虑如下甘油流加生物歧化为1,3-丙二醇过程的还原途径酶催化非线性动力系统:

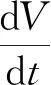
(9)

(pi=1,3-PD,HAc);

(i=GDHt,PDOR);t∈[0,tf].

其中:ρX是代谢物质量浓度,g·L-1;cs是底物浓度,mmol·L-1;cse,csi分别是反应器中胞外与胞内甘油浓度,mmol·L-1;c3-HPA为胞内3-羟基丙醛浓度,mmol·L-1;cPDi为胞内1,3-丙二醇浓度,mmol·L-1;μ,μm分别是比生长速率及其最大值,h-1;qPD,qHAc,qEtOH是产物比生成速率,mmol·g-1·h-1;qs是底物比消耗速率,mmol·g-1·h-1;cPD,cHAc,cEtOH是产物浓度,mmol·L-1;Vs为单位生物量细胞内体积,L·g-1;F为甘油流加速率,L·h-1;V为反应器中液体体积,L;r为碱的流加速率与甘油流加速率之比;t为发酵时间,h;tf是t的终端时刻,h;其余参数意义及取值参见文献[18].

2 最优控制模型

针对甘油生物流加发酵过程,建立了如下优化目标为终端时刻1,3-丙二醇浓度的最优控制模型:

3 求解方法

设

则可将式(10)表示为下列最优控制问题:

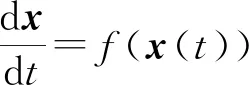
其中,Kx、Ku为有限元[ζi,ζi+1]上配置点的个数.上述多项式中的xKx(t)满足xKx(tij)=xij,uKu(t)满足uKu(tij)=uij.为确定多项式xKx(t)、uKu(t)的系数,将其代入状态方程中,可得如下方程:

令tik=ζi+Δζiτk,Δζi=ζi+1-ζi,τk∈[0,1],则可将式(12)、式(13)写为:

此外,为保证状态在有限元终端具有连续性,相邻有限元的初始状态与终端状态需符合以下条件:

因此可将最优控制式(11)转化为如下NLP问题:

4 结果与分析

图1为tf取20 h时,各变量随时间t的变化曲线.表1为不同终端时刻下,r取值为0.75时最优控制问题的最优解.随着终端时刻tf逐渐增大,ρX先逐渐增大,在20～28 h内逐渐减小,然后增大,在20 h达到最大值2.87 g·L-1;cs先减小后增大再减小,在32 h减小至977.36 mmol·L-1;cPD达到最大值939.50 mmol·L-1后不发生变化;cHAc的值先增大后减小再增大;cEtOH和c3-HPA变化趋势相似,都是先增大,然后在28～32 h内逐渐减小,两者最大值分别可达到68.01和551.80 mmol·L-1;csi的值先减小,在20～25 h内逐渐增大,然后减小;csi最大可达到1 168.71 mmol·L-1;cPDi的值先增大后减小再增大,在32 h升到最大938.61 mmol·L-1;V的值先增大,然后减小,最大可达到7.99 mmol·L-1;F的值先逐渐增大,在20～28 h内逐渐减小,然后再增大.

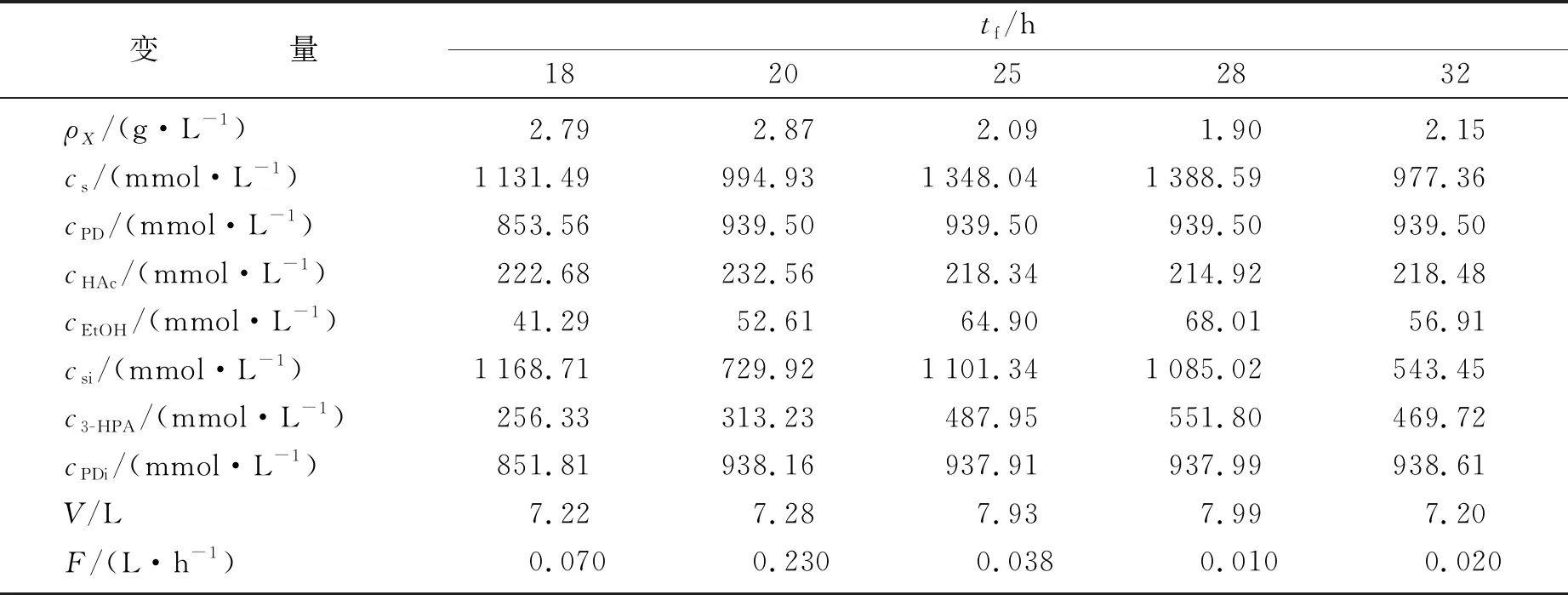
表1 不同终端时刻下最优控制问题的最优解Table 1 Optimal values of optimal control problem under different terminal moments

(a) ρX的变化曲线(b) cs的变化曲线(c) cPD的变化曲线(d) cHAc的变化曲线(e) cEtOH的变化曲线(f) csi的变化曲线(g) c3-HPA的变化曲线(h) cPDi变化曲线

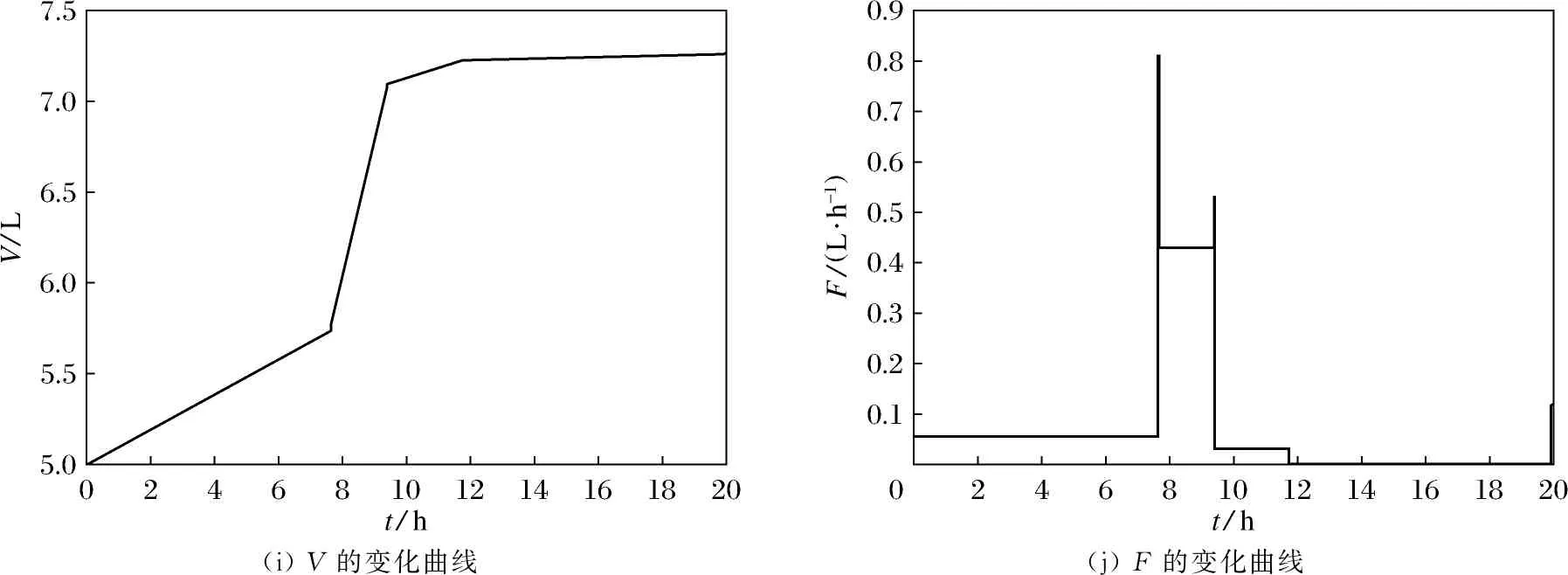
(i) V的变化曲线(j) F的变化曲线

5 结 语

本文以甘油生物歧化生产1,3-丙二醇过程的最优控制为研究背景,建立了固定终端时刻条件下,使1,3-丙二醇的最终浓度达到最大值的最优控制模型.基于有限元配置法求解了所建立的最优控制问题,得出了模型的最优数值.为实现甘油生物歧化过程的生产优化提供了指导与方法.