基于正则相关矩阵的信源数快速估计方法

郑巧珍, 成思文, 薛心竹, 周 栋

(上海无线电设备研究所,上海201109)

0 引言

现代战争的电磁作战环境日益复杂,目标及干扰的类型与数目越来越多,对雷达的空间分辨能力及抗干扰能力提出了新的挑战。因此,要求雷达天线必须有足够大的口径、辐射功率以及空间自由度,这些都促使阵列天线朝着大型化发展。对于大型阵列天线,若采用阵元级信号处理系统,一方面,需要架构复杂且体积庞大的硬件设施;另一方面,阵列处理技术的时间复杂度高,在体积、重量、处理能力受限的弹载平台难以实现。因此采用基于子阵的阵列雷达技术,在降低系统复杂度和成本的同时,保留了目标空域维信息,降低了阵列信号数据的维数,为阵列信号处理技术的应用提供了基础。

在阵列信号处理技术中,空间谱估计技术作为其中一个重要研究方向,在雷达、通信、声呐等众多领域皆有广阔的应用前景。空间谱估计技术的重要分支——波达方向估计(即目标入射角估计)日趋成熟。最初的波达方向估计是基于假设检验的[1-3],即需事先主观设定目标个数才可完成目标波达方向估计。为了避免这种主观性,在噪声统计特性已知的前提下,提出了基于信息论的方法,其典型代表是Akaike提出的赤池信息量准则(Akaike’s Information Criterion,AIC)方法[4]和Wax等提出的最小描述长度(Minimum Description Length,MDL)方法[5]。信息论方法虽解决了门限值选定的主观性问题,但一方面,带来了噪声统计特性的先验问题,噪声统计特性假设失配将带来判决失效[6];另一方面,信息论方法涉及相关矩阵的特征值分解,运算量较大。针对这一问题,Wu和Chen提出了一种不需要知道具体特征值的信号源数估计方法——盖氏圆(Gerschgorin Disks Estimator,GDE)方法[7-8]。但盖氏圆方法需要对分块矩阵进行特征值分解,而分块矩阵的维度仅比全维矩阵的维度少1,对信息论方法复杂度的改善并不明显。近年来,学者针对各应用条件,相继提出了基于以上方法的改进方法。如侯云山等提出了一种低信噪比下的信号源数检测新方法[9],但该方法需要利用波束形成器在空间做预扫描,在弹载平台难以满足实时性要求。综上所述,亟需研究一种实时性高、环境适应性强的信源数估计方法,以满足阵列雷达的波达方向估计要求。

1 信号模型

假设空间有S个窄带目标信号,对于N元面阵,t时刻阵列接收信号矢量

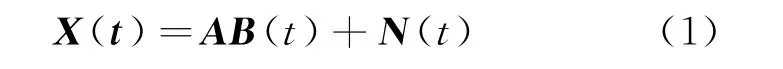
其中

式中:X(t)为N×1维接收信号矢量;A为阵列导向矢量矩阵,其维数是N×S;a(θi,φi)为第i个目标的阵元级导向矢量,θi,φi分别为第i个目标的入射方位角和俯仰角;δx,δy分别为方位维和俯仰维阵元间距;λ为波长;B(t)为目标信号的复包络矢量,其维数是S×1;bi(t)为第i个目标信号的复包络,i∈[1,S];N(t)为N×1维阵列接收的噪声矢量。阵面接收信号自相关矩阵为

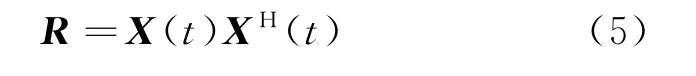
式中:H表示共轭转置。将N元面阵划分为M个子阵,则子阵级接收信号矢量可表示为

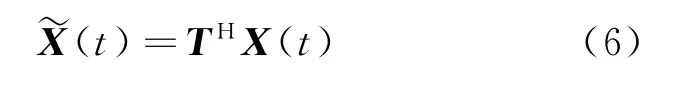
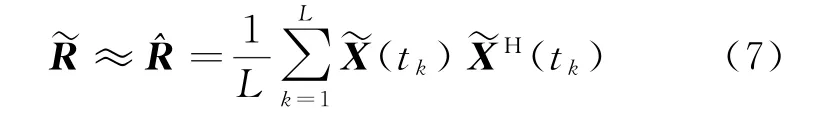
式中:L为快拍数;在tk时刻的取值。

2 信源数快速估计

多重信号分类(Multiple Signal Classification Algorithm,MUSIC)算法是Schmidtz在1979年提出的。该算法的基本思想是将空间分为信号子空间和噪声子空间,通过构造阵列协方差矩阵并进行特征值分解,得到特征值及特征矢量矩阵。其中大特征值及对应的特征矢量为信号因子和信号子空间,反之为噪声因子及噪声子空间。在窄带信号系统中,当信噪比趋于无穷大且快拍数远大于入射信源个数时,信号因子趋于1,噪声因子趋于0[10]。因此,统计特征值中趋于1的因子个数,即可得到信源数。实际应用中,信噪比及快拍数受限,因此信号因子与噪声因子无法明显区分,可根据虚警概率选定合适的门限值,采用MUSIC算法,可以得到信源数的估计值。

本文提出的基于正则相关矩阵的信源数快速估计方法,对雷达天线面阵进行二级子阵划分:第一级采用无重叠子阵划分方法,通过模拟功率合成,形成多个子阵级接收通道,降低系统硬件复杂度的同时降低阵列信号数据的维数;第二级采用正则子阵划分方法,对第一级子阵进行二次划分,按照轴对称等分为两个非重叠二级子阵。利用两个二级子阵接收的信号构建正则相关矩阵,并对正则相关矩阵进行特征值分解,得到该矩阵的特征值,该特征值也称作正则相关因子。

假设含M个接收通道的阵列雷达,两个二级子阵为子阵A和子阵B。子阵划分方式如图1所示。图中,r=(M/2)。

图1 子阵划分示意图

第一级子阵的接收信号矢量为

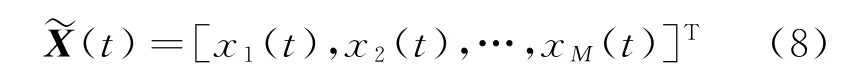
式中:“T”表示转置;xi(t)为第i个接收机通道输出的信号。

第二级子阵的接收信号矢量为

则第一级子阵的自相关矩阵可表示为

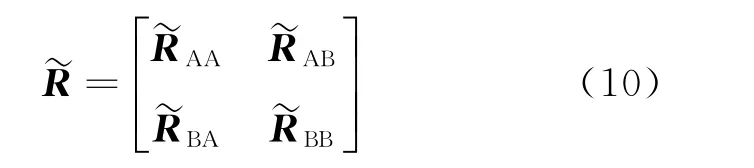
式中:为r×r维方阵。对进行特征值分解,得到该矩阵的r个特征值满足

特征值λi(i=1,2,…,r)为子阵A与子阵B接收信号的正则相关因子。当噪声满足高斯分布时,特征值λi满足Bartlett近似,定义序列

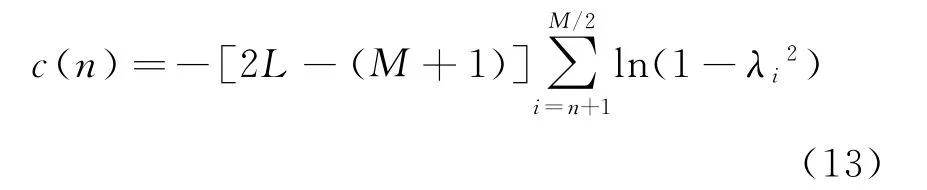
式中:n为序列变量,n∈[1,r-1]。c(n)近似服从自由度为m(n)的卡方(χ2)分布,m(n)=2(r-n)2。

对于χ2分布,设T(n)为相关因子门限,虚警概率Pf与积分区间[T(n),∞)的对应关系为

其中

对于任意一个n,可得到对应的m(n)和c(n);根据m(n)和设定的Pf,可得到T(n);对比c(n)和T(n),当c(n)≥T(n)时,信源估计个数满足设定的虚警概率,此时的n即为所估计的信源数。

本文假设噪声服从高斯分布,高斯随机变量的平方服从卡方分布。若噪声不服从高斯分布,可根据实际分布特性得到概率密度函数。文中方法对噪声功率密度函数不做要求,因此适用于白噪声和色噪声,具有更强的环境适应性。

本文方法对进行特征值分解的时间复杂度为o(M3/8);AIC方法、MDL方法的时间复杂度为o(M3);GDE方法的时间复杂度为o((M-1)3)。因此,本文方法有效缩短了信源数估计时间。从式(11)可以看出,信源数的取值范围在0和(r-1)之间,这是由于本文方法将子阵做了二级划分,自由度减小,可分辨目标个数随之减少。

3 仿真结果

通过仿真比较本文方法、AIC法、MDL法、GDE法的性能。假设某相控阵雷达导引头天线阵采用方形面阵,阵元数为12×12,行间距和列间距均为半波长。阵面划分为16个一级子阵,每个子阵均为阵元数为9的方阵。阵面按水平轴对称划分为上下2个二级子阵,每个二级子阵内含8个一级子阵。二级子阵划分后,俯仰维自由度由4降为2,俯仰维可分辨目标数降为1。仿真中3个目标俯仰角都设为0°,主波束指向(0°,0°),信号源数为3,入射信号俯仰角均为0°,方位角分别为-4°,1°,5°,虚警概率为0.001,独立试验次数100次。高斯白噪声协方差矩阵为单位矩阵。高斯色噪声协方差矩阵为三对角矩阵,其中主对角线值为1,高低对角线值为0.2。

图2为高斯白噪声背景下,各方法检测成功概率随信噪比变化曲线图。从图中可以看出,在白噪声情况下,本文方法与AIC法性能相当,优于MDL法和GDE法。

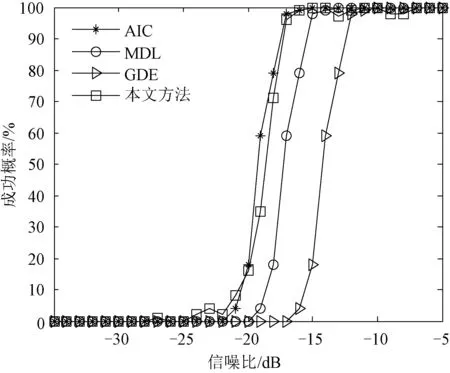
图2 高斯白噪声下,检测成功概率随信噪比变化曲线图

图3为高斯色噪声背景下,各方法检测成功概率随信噪比变化曲线图。从图中可以看出:在色噪声背景下,由于噪声统计特性与信息论方法的先验信息——白噪声不匹配,AIC法和MDL法失效;在低信噪比情况下,本文方法估计性能优于GDE方法。综上所述,本文方法具有较好的估计性能及环境适应性。

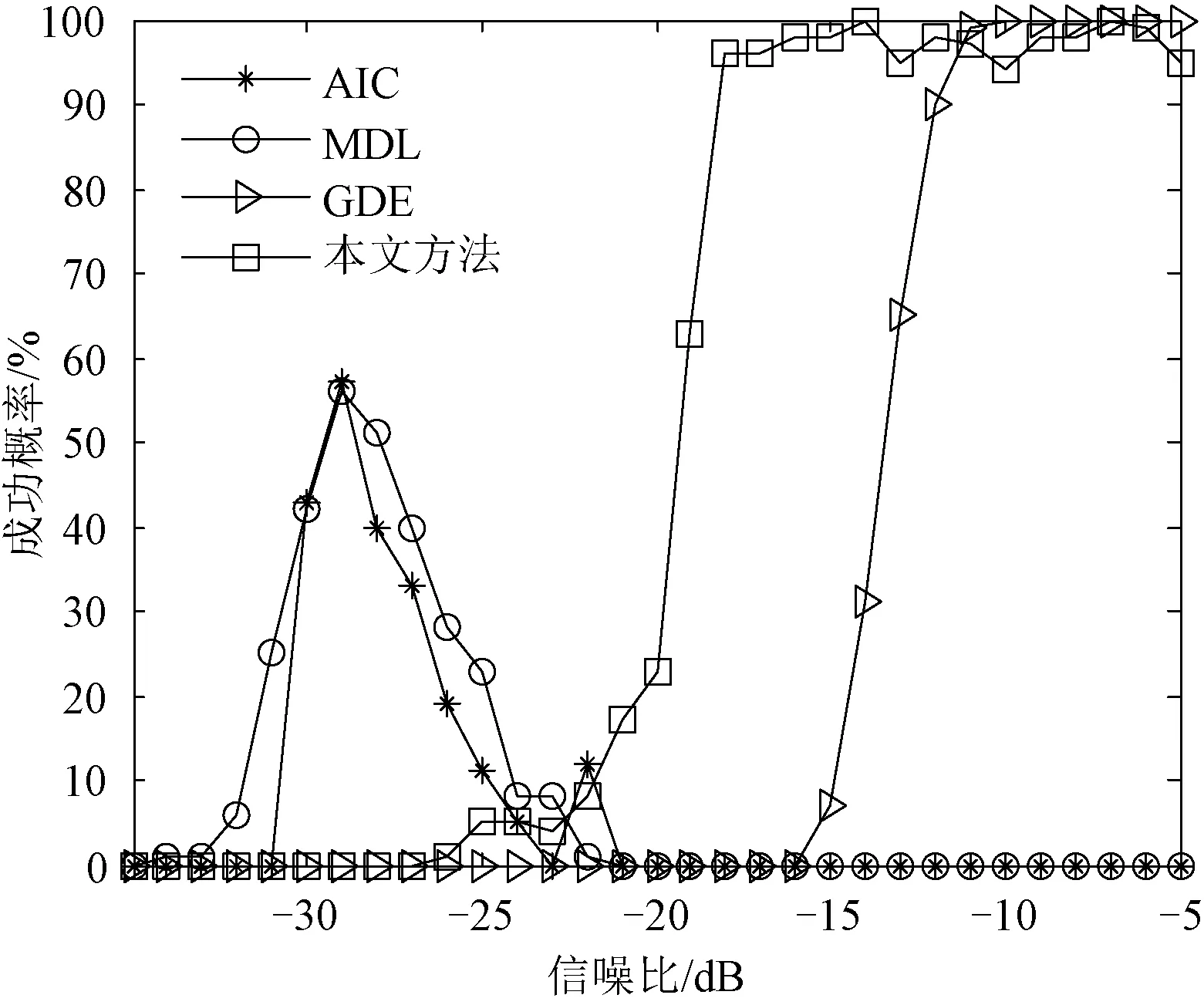
图3 高斯色噪声下,检测成功概率随信噪比变化曲线图

4 结束语

本文提出一种基于正则相关矩阵的信源数快速估计方法。该方法将阵列雷达的接收通道划分为子阵数相等的两个二级子阵,利用这两个二级子阵的接收信号构建正则相关矩阵,并得到两个二级子阵接收信号的正则相关因子。正则相关因子由信号因子和噪声因子两部分组成,大相关因子个数为信源数。利用这一特性,选定相关因子门限,即可得到信源个数。仿真试验验证了方法的有效性。该方法易于工程实现,时间复杂度仅为基于信息论的AIC方法和MDL方法的八分之一。但由于本文方法将子阵做了二级划分,降低了可分辨目标个数。