运用向量简证三角形内心坐标公式
2020-08-24 04:42:54武增明
数理化解题研究 2020年22期
武增明
(云南省玉溪第一中学 653100)
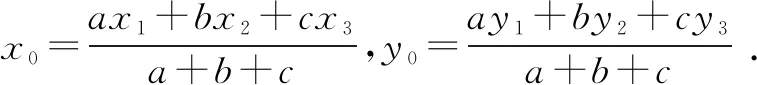
为了便于广泛交流,把此结论称之为三角形内切圆圆心坐标公式,即三角形内心坐标公式.
三角形内心坐标公式,文字表述简洁,符号表述漂亮,结构优美,十分有趣,让人赏心悦目,享受到数学之美,感受到数学的魅力,且有着广泛的用途.由此引起笔者极大的探究兴趣与热情,笔者查阅了大量的资料,没有找到三角形内心坐标公式的证明记录.笔者反复思考,反复推算,调整思维,受文[2]的启示,笔者想到运用向量探究三角形内心坐标公式的简证,获得成功,形成此文,与大家分享、共赏.
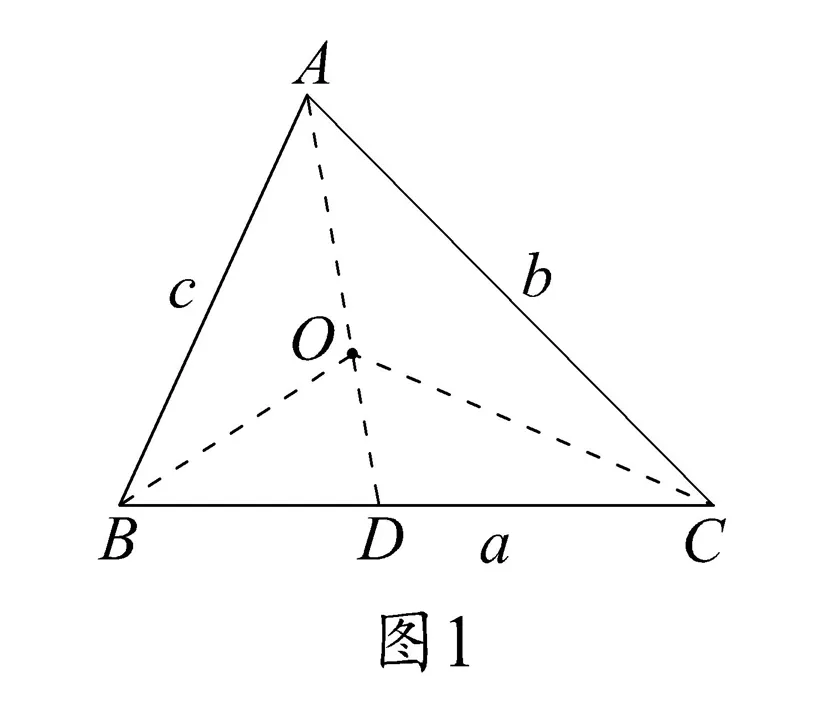
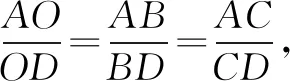
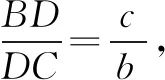

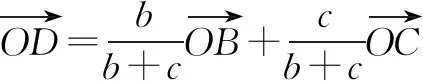
因为A(x1,y1),B(x2,y2),C(x3,y3),O(x0,y0),
所以由③,得a(x1-x0,y1-y0)+b(x2-x0,y2-y0)+c(x3-x0,y3-y0)=0,即(ax1-ax0+bx2-bx0+cx3-cx0,ay1-ay0+by2-by0+cy3-cy0)=0,
所以ax1+bx2+cx3-(a+b+c)x0=0,ay1+by2+cy3-(a+b+c)y0=0,
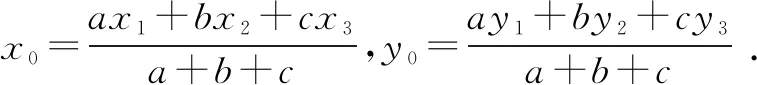
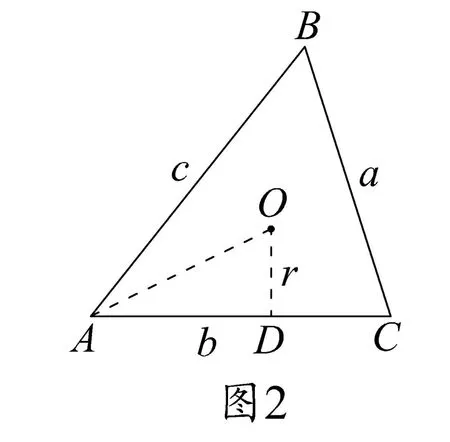
简证2 连接AO,作OD⊥AC交边AC于点D,如图2.设△ABC的内切圆半径为r,则OD=r.
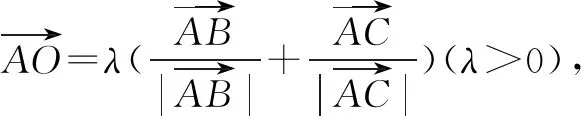
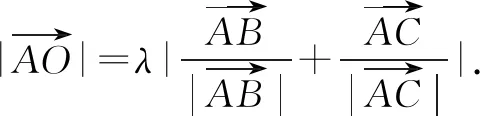

=2+2cosA

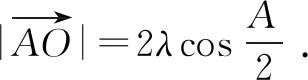
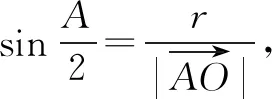
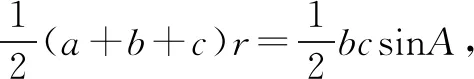
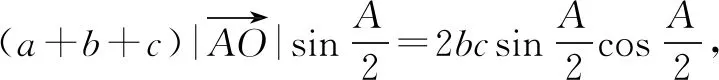
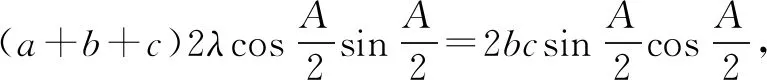
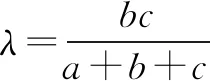
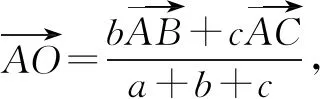
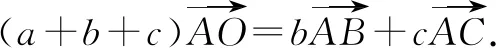
因为A(x1,y1),B(x2,y2),C(x3,y3),O(x0,y0),所以(a+b+c)(x0-x1,y0-y1)=b(x2-x1,y2-y1)+c(x3-x1,y3-y1),
故而(a+b+c)(x0-x1)=b(x2-x1)+c(x3-x1),
(a+b+c)(y0-y1)=b(y2-y1)+c(y3-y1),
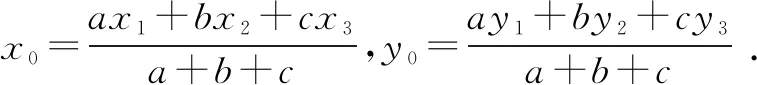
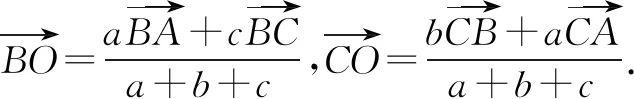
猜你喜欢
新高考·高一数学(2022年3期)2022-04-28 07:02:46
中等数学(2021年2期)2021-07-22 06:21:52
中学生数理化(高中版.高考数学)(2021年1期)2021-03-19 08:28:36
中等数学(2020年9期)2020-11-26 08:07:28
中等数学(2018年7期)2018-11-10 03:29:04
文理导航·科普童话(2017年7期)2018-02-10 19:42:29
中学数学杂志(高中版)(2018年1期)2018-01-27 18:49:49
小天使·四年级语数英综合(2017年6期)2017-06-07 10:45:55
小天使·二年级语数英综合(2017年3期)2017-04-01 20:49:17
小学生导刊(低年级)(2016年6期)2016-07-02 22:16:01

