考虑多目标件的异步并行选择性拆卸序列
邓明星,陈方颖,唐秋华,陈 刚
(1.武汉科技大学 汽车与交通工程学院,湖北 武汉 430081;2.武汉科技大学 机械自动化学院,湖北 武汉 430081;3.武汉东风鸿泰汽车资源循环利用有限公司,湖北 武汉 430081)
0 引言
拆卸指将零部件从产品上分离的过程。根据零部件拆卸的逻辑次序,拆卸可以分为并行拆卸和串行拆卸,串行拆卸是指将零部件依次顺序拆卸,且一次仅拆卸一个零部件;并行拆卸则是指多个零部件可同时被拆卸。进一步而言,根据任务的执行方式,并行拆卸可分为同步并行和异步并行,两者区别在于任务开始时间,同步并行是同时开始执行并行的拆卸操作,而异步并行是各自即时开始执行并行的拆卸操作,节省了等待其他任务完成的时间。在对复杂产品进行拆卸时,异步并行能减少整体拆卸时间,更具有实际指导意义。产品拆卸按拆卸程度可分为完全拆卸和选择性拆卸。选择性拆卸多用于产品维护,或是在报废后具有较大再利用价值的产品回收。本文针对多目标件异步并行选择性拆卸问题,通过对其序列规划确定需拆卸的零部件及其拆卸步骤,达到降低成本、提高效率与环境效益的目的。
目前,国内外学者对于选择性拆卸序列规划问题已有丰硕的研究成果。Kara等[1]采用图论方法枚举所有可行序列,并选取所需选择性拆卸序列;丁勇等[2]采用基于规则消除不可行的序列,并通过递归方法求解拆卸序列;Wang等[3]和Luo等[4]均构建了多层约束矩阵,以减少选择性拆卸规划的搜索范围,后者进一步用蚁群算法求解了复杂产品拆卸问题;蔡凯骏等[5]在分析零部件可拆卸性的基础上,通过分层图方法定位目标零件,去除多余拆卸步骤并将选择性拆卸转化为完全拆卸序列规划。针对多目标件问题,Smith等[6]通过规则生成多个独立的单目标件拆卸序列结构图,依据其特征点融合形成一个最小规模的多目标件结构模型;文献[7-8]考虑了多个目标件的情况,并通过递归推理得到最小零部件集合或是直接在递归过程中生成序列。选择性拆卸逐渐受到重视并得到深入的研究,通过递归方法处理选择性拆卸序列规划这类问题较为常见且有效,但目前针对多目标件问题的研究仍较少。
并行拆卸的序列规划问题在近年来也受到了普遍关注与深入研究,很多学者就并行拆卸序列规划问题展开了研究。Zhang等[9]构造了并行拆卸的模糊粗糙集映射模型并寻优;田永廷等[10]和张秀芬等[11]采用遗传算法,以拆卸单元序列和拆卸步长作为编码的前段和后段,确定了每一步所需拆卸的零部件,以表示并行序列的初始种群个体;蔡凯骏等[12]运用蚁群算法,以多只蚂蚁表示相同数目维修人员共同参与拆卸,以此研究一条并行拆卸序列。上述文献在考虑并行拆卸时,通常要求在完成当前任务时,等待同步执行的其他所有任务完成后,才能同时执行下一步并行任务。但在实际拆卸过程中,不违背各种约束关系的情况下可以直接进入下一步操作。Ren等[13-14]提出协同拆卸的概念,进一步提出了同步和异步并行拆卸的概念及区别,并用双向量列表结构进行编码与解码求取可行序列,但需对列表依次更新,以生成可行序列,且在保证约束的前提下进行交叉操作的过程较为复杂。
本文基于异步并行拆卸概念,提出了考虑多目标件的异步并行选择性拆卸序列规划方法。针对多目标件选择性拆卸,确定了拆卸零部件集合;构建了异步并行拆卸序列规划数学模型,并基于改进遗传算法,以拆卸完工时间为目标,获取了满足需要的近优甚至最优拆卸序列规划方案。
1 拆卸信息模型构建
1.1 拆卸基本信息表达
有向图由有向边和节点组成,常被用于简洁有效地表达产品拆卸优先关系。优先关系示意图如图1所示,可表示为EG={V,E},其中:V为最小拆卸单元集合,E为有向边集合。节点i表示产品中的最小拆卸单元,有向边连接各个节点,ei,i′∈E,表示零件i优先于零件i′拆卸。拆卸优先级较节点i高,且与之相邻的所有节点构成i的直接前序集合Γ。图1中有向边e4,9和e5,9即表示零件4和5需优先于9拆卸;节点9的直接前序集合则为{4,5}。
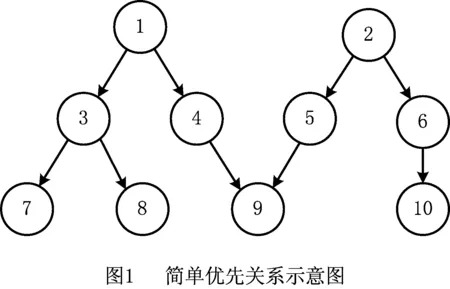
其邻接矩阵可表示为P={pi,i′},当ei,i′∈E时,pi,i′=1,否则pi,i′=0。以图1为例,e4,9∈E,故p4,9=1。干涉矩阵表示为CD(D=x,y,z)={ci,i′},则D方向上的干涉矩阵中,若零件i在沿+D方向拆卸时与i′发生干涉,即零件i′在沿-D方向拆卸时与i发生干涉,则ci,i′(ci′,i)=1,否则取0。
拆卸时间包括基本拆卸时间和辅助拆卸时间,其中前者为拆卸零部件所耗费的时间,后者本文只考虑拆卸方向改变所需的时间。拆卸方向在±x,±y,±z这6个方向上移动,则辅助时间可表达为Dir={di,i′},其中:di,i′=0(单位:s),表示拆卸方向不改变;di,i′=1时,表示拆卸方向转变90°;di,i′=2时,表示拆卸方向转变180°。
1.2 待拆零部件集合及其相关拆卸信息获取
零部件间的优先关系具有传递特性,而选择性拆卸是针对目标件的一种定向操作,需拆卸所有对目标件有阻碍关系的零部件,直至目标件被拆卸。基于优先关系的传递特性,以目标零件为起始点,回溯前序零件,以获取阻碍目标件拆卸的所有零部件。设O为多目标件集合,S为待拆零部件集合,A用于缓存,具体步骤如下:
步骤1初始化,S=∅,A=∅,将目标件置于集合O中。
步骤2判断O是否为空集,如果O不为空,从集合O中选取目标件o,置于集合S中,并从O中删除;如果为空集,则转步骤7。
步骤3判断o是否可拆,如果是,则转步骤2;否则,将其直接前序Γ置入集合A。
步骤4判断A是否为空集,如果是,转步骤2;否则,转步骤5。
步骤5判断A中元素a是否已存在集合S中,如果存在,则转步骤4;否则,转步骤6。
步骤6判断A中元素a是否可拆,将其从A中删除并置入S中,如果可拆,转步骤4;否则,将其直接前序Γ置入A中,转步骤5。
步骤7输出集合S。
2 考虑多目标件的异步并行拆卸序列规划问题建模
2.1 问题描述
考虑多目标件的异步并行选择性拆卸序列规划问题可描述如下:设待拆装配体含有K个待拆卸单元。为高效拆卸某个或某些目标件,以总体拆卸时间最小为目标,并行序列总数为R,要求确定目标函数最小的拆卸序列,且满足约束条件:①优先关系约束;②所有的目标组件均被拆卸;③所有最小拆卸单元只被拆卸一次。
根据所描述问题,可给出如下假设与说明:①每个拆卸任务不可中断;②在同一时刻只能拆卸一个零件;③拆卸过程无破坏。
2.2 考虑多目标件的异步并行拆卸序列规划数学模型构建
根据上述问题描述可建立数学模型如下:
minmakespan。
(1)
(2)
(3)
(4)
(5)
(6)
∀pi,i′=1,pi,i′∈P,ci,i′=1,
ci,i′∈C,∀r,r′,n,n′,i,i′;
(7)
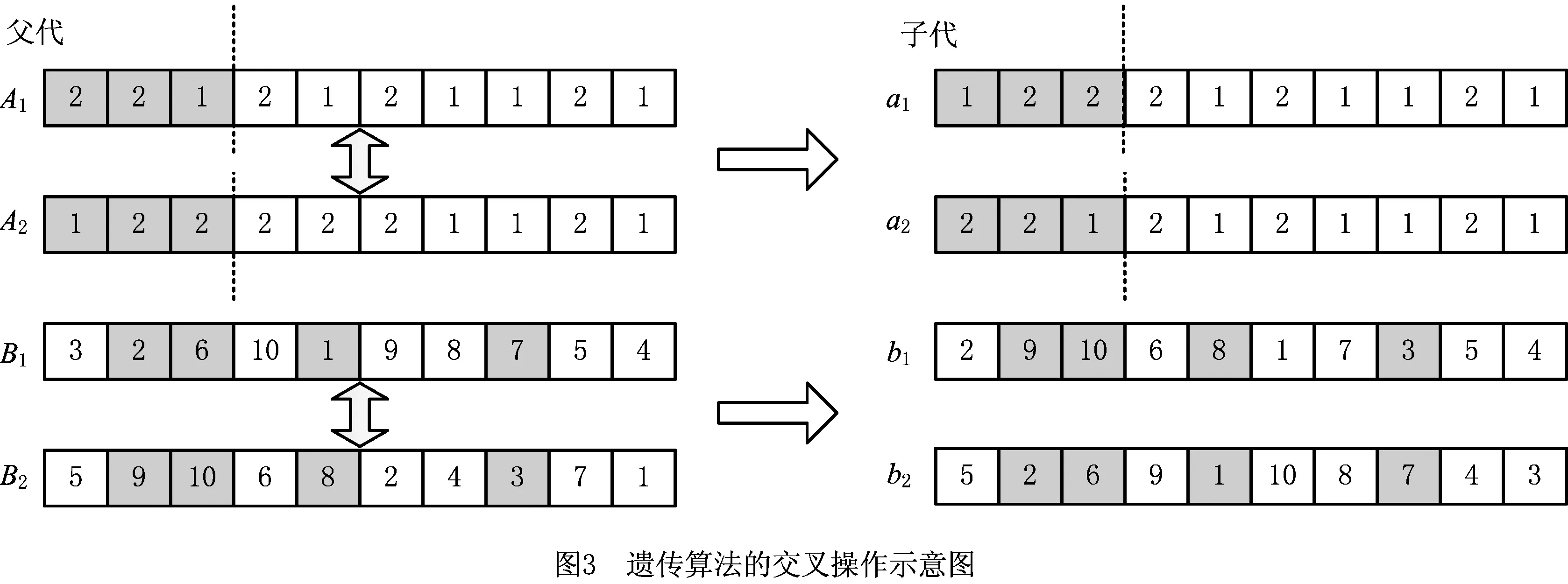
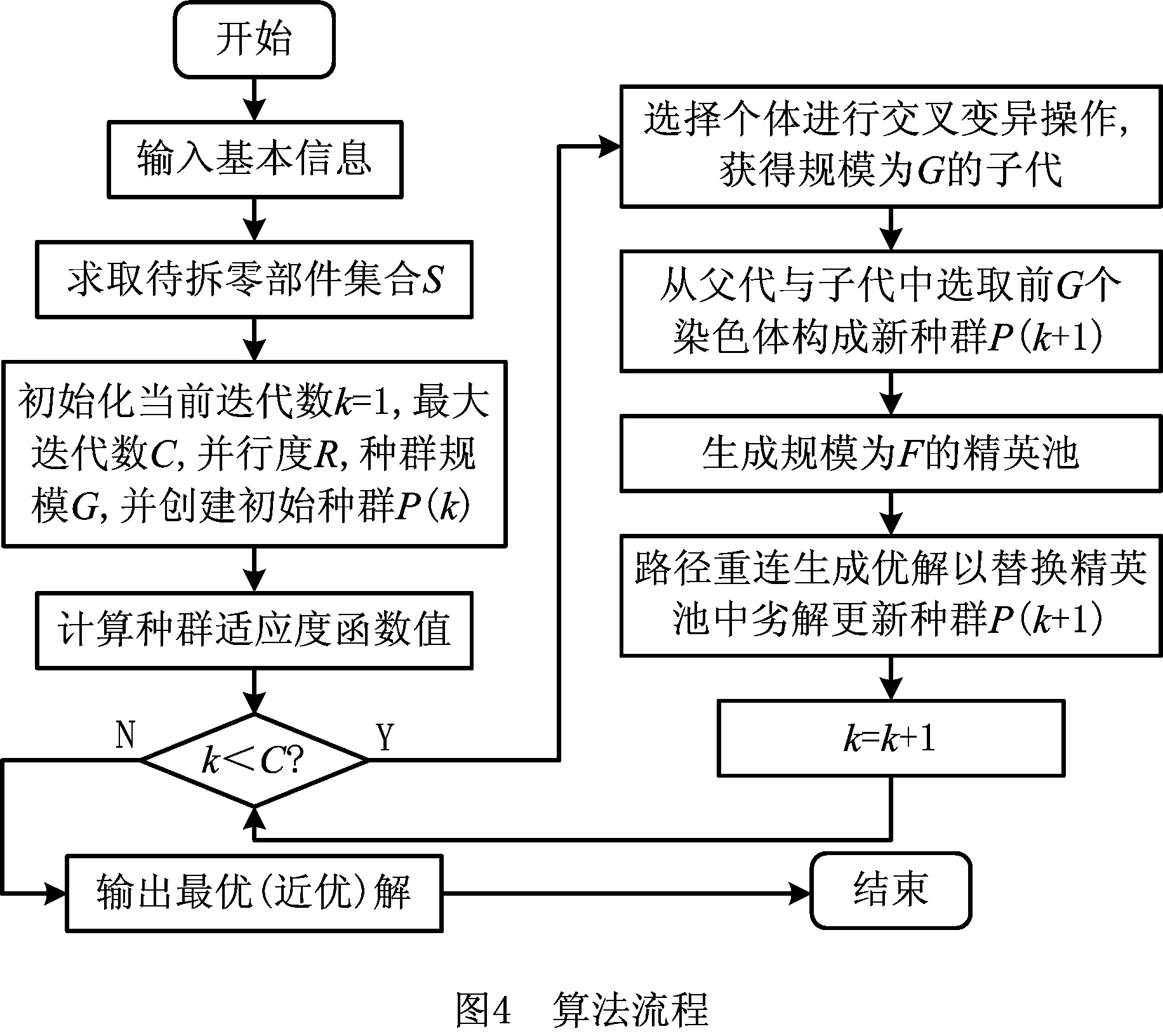
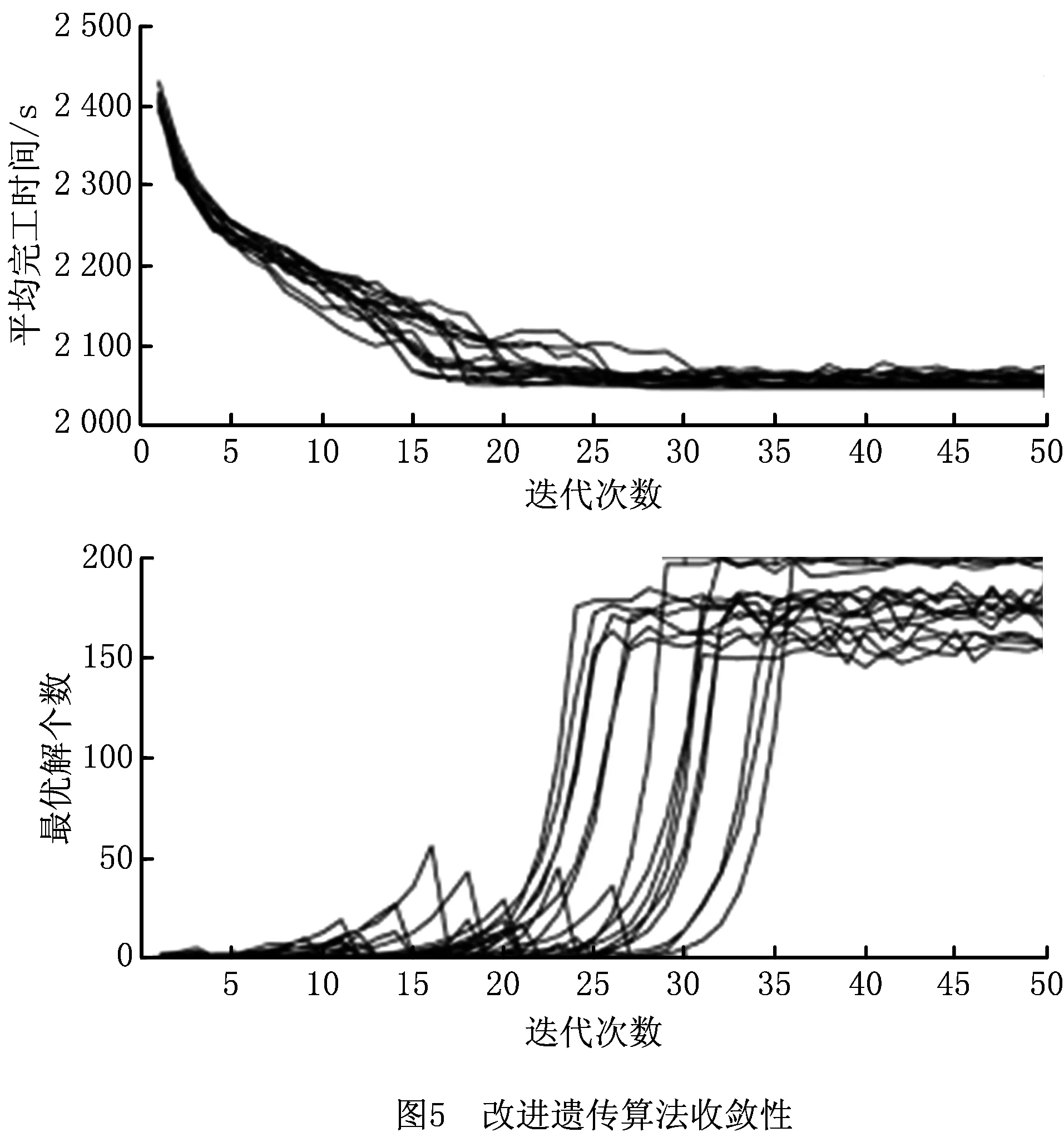
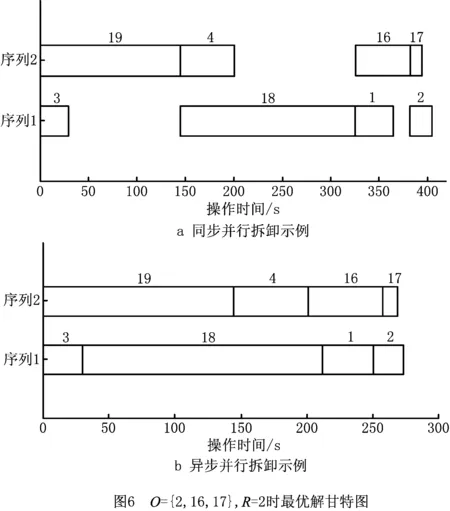
∀i,i′,r,n (8) 式(1)表示目标函数,为最小化拆卸完工时间;式(2)保证每个拆卸任务都必须被执行;式(3)表示对于每个并行序列的每个拆卸任务最多仅能进行一次拆卸;式(4)保证每个并行序列必须执行至少一次拆卸操作;式(5)保证在前一个任务执行了以后才能执行下一个拆卸任务;式(6)表示每个任务的拆卸开始时间和拆卸结束时间之间的关系;式(7)表示仅在两个任务i和i′存在优先关系并考虑干涉时,任务i的结束时间必须在i′的开始时间之前;式(8)保证并行序列下只有在前一个任务及辅助操作执行完毕之后,才能继续执行下一个任务。 启发式算法因能高效求解大规模问题的近优解,近年来被广泛应用于拆卸序列规划研究中。本文融入路径重连策略,采用改进遗传算法进行多目标件的异步并行选择性拆卸序列规划。 染色体采用两段式编码,包括并行序列的序列分配段和任务排序段,分别简称为v1和v2,且长度均为K,其编码如图2所示。v1中每个基因均由随机生成的操作人员序号组成;v2由K个任务执行序号随机排列生成,生成新的v2则对任务的执行顺序进行了重新分配,且任务的人员分配与v1中同一位置的元素是一一对应的。 解码需首先取v2中序号为1的任务,判断其对应零件是否可拆。若可拆,将任务分配给对应v1段的并行序号,获取被分配任务的开始与结束时间,并将该任务赋零值;否则顺次对下一序号为2的任务进行判断。当对v2分配到最末任务时,返回至序号最小且不为零的任务,并重复上述操作,直至所有任务均被分配。最后读取相应数据,将v2任务对应于被拆卸零件,可得到所求序列。 目前常见交叉算子主要包括单点交叉、两点交叉、多点交叉和均匀交叉,依据两段编码的各自特点,需分别对两段编码执行不同的交叉操作。在v1段主要采用单点交叉的方法,随机选取一个交叉点,将两个父代的基因段从交叉点断开并交换前段,即可获得两个子代。在v2段依据编码特点选择均匀交叉方法,使每一位基因都能够以相同的概率进行交换。因序列长度不定,均匀交叉相对于选择单点交叉表现效果更优。具体交叉方法为:将第一个父代交叉点的基因同第二个父代交换,得到子代的一部分;寻找父代未被交换的基因,并依次放入子代空白部分,将子代剩余部分填充完整。编码与解码方法使得无论以怎样的顺序组成染色体,都可解码获取可行序列,因此上述变异过程生成的仍为由1-K组成的可行解。 如图3所示为v1和v2两段编码对应的两种交叉操作示意图。图中,以A和a指代序列分配段,B及b指代任务排序段。首先在父代A1和A2上选取交叉点,以交叉点为分界线将A1与A2进行分割,并将前段灰色基因{2,2,1}与{1,2,2}进行交换,虚线后段白色部分不变,则可得到子代a1,a2。随后在父代B1上随机产生4个交叉点,将B2灰色交叉点的基因{9,10,8,3}置于b1相同位置,再在B1中找到除{9,10,8,3}以外的基因,将其顺次放入b1白色位置上,则生成完整子代b1,生成b2方法类似。此处须知,对于所生成的b1和b2,仅需保证其为1~10的数字随机打乱组成的序列,即可依据3.1节所提的解码规则获取可行的拆卸序列。 在v1段选取一个变异点,并将变异点处元素变换为其他并行序列;随机交换v2段两个变异点处的元素,完成变异操作。 如前所述,所提编码与解码方法生成初始解过程简单且可行,生成的解具有多样性,且对其进行交叉变异后可直接生成可行解,具有易操作性。 基于所获取的待拆零部件集合及上述编码规则,即可初步生成初始种群。初始种群需要通过优胜劣汰法则选取其中精英解,在种群更新与淘汰过程中优化整个种群,直至达到所设定的迭代次数。适应度函数用于评判种群中个体的优劣,从而保护较好的染色体不被淘汰。此处,以chro表示染色体编号,拆卸序列规划中的第i项任务结束时间为fti,考虑拆卸方向更换的时间,则可将相应适应度函数定义为f(chro)=max{fti}。解码后可得各个拆卸任务结束时间,并求取适应度函数值,该数值越小,其对应染色体的质量越优。 设种群规模为G,从父代种群中选择个体进行交叉与变异操作,产生与父代种群规模相同的子代。通过适应度函数值衡量种群内染色体优劣,并选择前G个高质量染色体作为父代进入下一轮循环。 路径重连策略是一种通过在初始解和引导解之间建立路径,获取路径生成过程中可能产生的更优解,以加速收敛的种群强化策略。文献[15-17]对于路径重连均有较好的实现。 进行交叉变异的操作产生新种群后,依据目标函数值对解进行排序,从排序高的解中获取规模为F的精英池,并从精英池中任取两个染色体作为初始解Si与引导解Sg。针对两段式编码,需对v1段和v2段分别引入元素。首先在v1段,以引导解中的一个元素替换v1段相同位置的元素,计算目标值后再对v2元素进行替换。直接替换v2元素后必然会产生重复元素,故以缺失元素替代重复元素。随着对v1与v2段的元素引入,初始解与引导解将达到一致,则重连结束。最后,比较新生成一系列解的目标函数值,用生成的最优解替代初始解。 每次从精英池中选取一对解,路径重连结束后将其从精英池中剔除,当精英池为空时结束重连。路径重连会有目的地将较优解中的元素重新组合,以期在该过程中获取更好的解来优化种群,具有一定的导向性。引入路径重连策略后,使所提方法能在较短的迭代次数内寻获较好的解,提高了求解效率。 本中所述方法的基本流程如图4所示。 本文以文献[18]中的发动机为研究案例进行分析对比,并结合所提出的改进遗传算法,于MATLAB中实现了考虑多目标件的异步并行拆卸序列规划。最大迭代次数C=50,种群规模Pop=100,交叉概率Pc=0.7,变异概率Pm=0.2。针对本文所考虑的异步并行选择性拆卸问题,假设目标件O={2,16,17},R=2,用GAMS软件求解所建数学模型,运行模型后获得序列(19,4,16,17)和(3,1,18,2),完工时间为273,结果表明所求得解与GAMS计算所得结果一致,从而验证了所提方法的可行性。当目标件和并行度取不同值时,计算结果如表1所示。 表1 目标件及并行度不同时所得最优解 以目标件为{2,26,33},并行序列R=3为例进行计算,运行15次,分别记录其每次迭代所得解的平均值和最优解的个数。如图5所示,算法在迭代25次左右可获取近优或最优解,且能较快收敛,表明了所提方法的高效性。 与文献[18]结果进行对比,在考虑异步并行拆卸后可获取的最短完工时间为2 048 s,最终完工时间缩短到了原文献的55.56%,极大地提高了拆卸的效率。由表1还可看出,R增大时完工时间有明显下降,但当R达到某临界值时,拆卸完工时间收敛。因此R值并非越大越好,可依据实际需要选择R数目。 当目标件为O={2,16,17}且R=2时,针对所求解绘制甘特图进行分析,如图6所示。图6中横坐标表示时间(单位:s),纵坐标为并行序列,矩形框上方数字表示待拆卸零件的序号,其中零部件之间所存在的间隙为辅助拆卸时间。图6a中同步并行拆卸总耗费时间为405 s,而图6b中异步并行在完成当前拆卸后立即执行下一可执行任务,总耗费时间为273 s。可以看出,异步并行时间得到了有效利用,操作也更为紧凑,提高了拆卸效率。 目前研究主要侧重于同步并行拆卸序列规划方面,但是实际拆卸过程往往是异步并行拆卸,因此,对于异步并行拆卸的研究更具有实际参考意义与工程价值。为提高并行拆卸序列规划效率,本文提出一种基于遗传算法的异步并行选择性拆卸序列规划方法,该方法具有以下特点: (1)采用有向图来描述产品零部件之间的拆卸优先关系,结合邻接矩阵、干涉矩阵与前序集合等,便于在计算机中通过递归方法求取包含多个目标件的待拆卸零部件集合。 (2)以所获取的待拆零部件集合为基础,总体拆卸时间最小为目标,确定目标函数最小的拆卸序列,并考虑异步并行拆卸序列规划问题的特点,构建了相应的数学模型。 (3)针对异步并行拆卸所具有的特点,采用包含序列分配段及任务排序段两部分的编码方法,并融入路径重连思想以改进遗传算法,最后通过案例验证了所提方法的可行性与有效性。 后续在对拆卸序列规划领域的研究中,需寻求更优的信息模型,通过具体实验验证,使其具有更强的实践性;针对多目标优化问题,文中考虑因素较少,且求解方式简单,需完善并优化求解方法;可考虑拆卸工具并行性及高效专用拆卸工具的使用对拆卸序列规划问题的影响。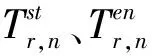
3 考虑多目标件的异步并行选择性拆卸序列规划算法研究
3.1 编码和解码方法
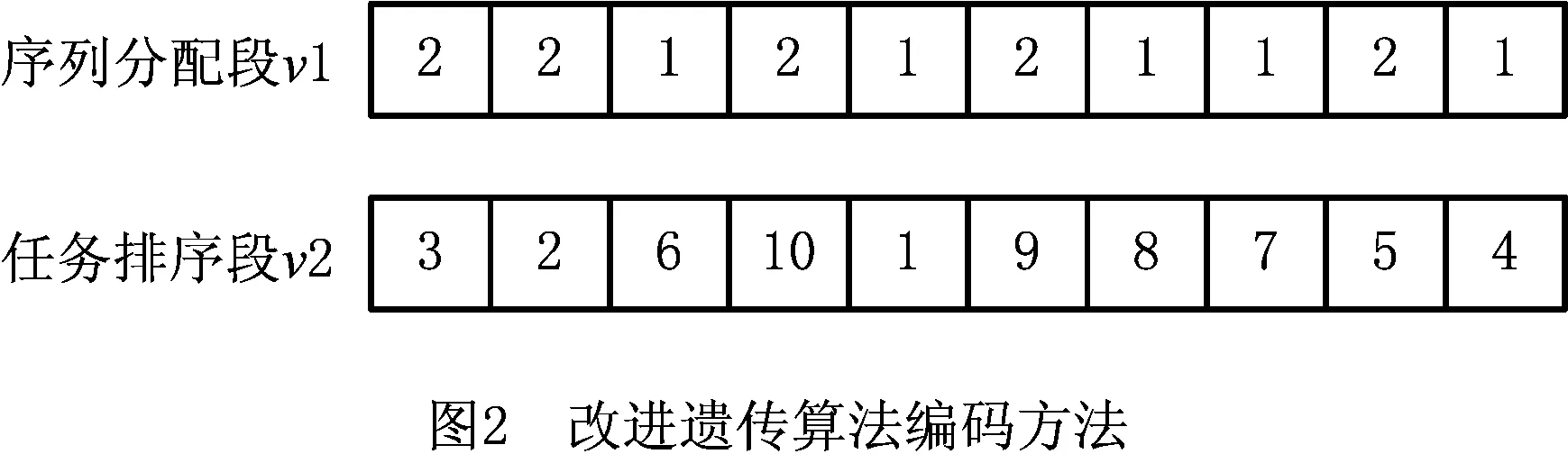
3.2 交叉与变异
3.3 适应度函数
3.4 路径重连策略
4 案例分析

5 结束语
——基于人力资本传递机制
——基于反向社会化理论的实证研究
——基于子女数量基本确定的情形

