基于核密度估计的实时剩余寿命预测
张卫贞,曾建潮,石 慧,董增寿
(1.太原科技大学 工业与系统工程研究所,山西 太原 030024;2.中北大学 大数据学院,山西 太原 030051)
0 引言
随着机械设备朝着大型化、自动化、精密化方向的不断发展,故障发生的可能性和故障类型的复杂性也随之增加,设备的突然故障可能导致整个生产流程中断,产生重大经济损失,甚至危及人身安全。因此,对机械设备的关键部件进行实时监测及剩余寿命的预测具有非常重要的现实意义。现有剩余寿命预测方法主要包括:物理模型、基于专家知识的模型和基于数据驱动的预测模型等。对于复杂的机械设备,建立物理模型往往十分困难,所获得的专家知识也不完备,因此,基于数据驱动的寿命预测方法逐渐受到重视[1-8]。
Huang等[9]利用支持向量机建立退化模型,用于预测剩余寿命;Chryssaphinou等[10]将部件的退化状态建模为离散的半马尔科夫过程;Si等[11]对关于数据驱动方面的回归模型、比例风险模型、随机滤波模型和隐马尔科夫等剩余寿命预测模型进行了综述。许多表征系统磨损或裂纹发展的单调退化过程被建模为Gamma过程[12-14],但这些数据驱动的实时剩余寿命预测方法,往往都需要进行退化模型的假设与参数估计。假设的退化模型与实际模型之间往往存在较大差距,且参数估计的最优化有可能收敛到局部最小却不能保证全局最优,因此预测模型并不能保证最终渐近收敛于真实的样本模型。
核密度估计方法是一种数据驱动的方法,但该方法对数据分布的形式不作任何假定,是从数据本身出发研究数据分布特征的非参数估计方法[15-16]。核密度估计方法常用于分类中,Zhang等[17]提出一种对旋转机械的故障类型进行区分的方法,对表征类型故障的特征,通过加入测试样本前后概率密度相对熵之间的比较,来判断属于哪种类型的故障,其中利用核密度估计的方法求概率密度;李存华等[18]提出一种基于核密度估计的数据聚类分析方法,对基于网格数据重心分箱后的数据点进行核估计,来构造高效的聚类算法。也有研究将核密度估计用于动态模型,文献[19-20]利用核密度估计对风速模型进行构建,有效降低了传统研究需要假设风速服从某种已知分布导致的误差。目前,关于核密度估计用于寿命预测的研究相对较少,Xu等[21]在基于Bayes的实时寿命预测中,采用实时退化特征信息的核密度估计来估计参数的先验分布;王洁[22]提出了基于核密度估计的气缸疲劳寿命预测,在已知N个气缸样本失效循环次数的前提下,利用核密度估计求任意第i个气缸失效时循环次数服从的概率密度,再利用循环次数的可靠度和平均剩余寿命结果对核密度估计方法和Weibull分布两种方法进行了比较。该方法是针对有多个同类设备历史数据的情形,然而实时寿命预测中,越来越多的现代设备并没有大量同类设备的历史退化数据。
本文针对实时监测系统,利用当前时刻的状态监测信息和历史信息,提出一种基于核密度估计的实时剩余寿命预测方法。首先,针对基于固定窗宽的核估计求样本概率密度时,容易造成样本数据少的地方拟合不足,而样本数据多的地方拟合过度的问题,改进为根据样本数据的密度自适应地选择窗宽值进行核密度估计,即高密度区域采用较大的核窗宽,而低密度区域采用较小的核窗宽,以提高核密度估计的准确性;其次,随着实时监测的进行,监测到的样本数据不断增多,样本的核密度估计也随之不断更新,采用传统的核密度估计模型时,每新增一个样本数据,基于这些样本的核密度估计都要重新计算,这样会造成历史样本不断重复计算,计算量也越来越大,为避免实时监测系统中样本核密度估计不断重复计算的问题,本文提出了核密度估计模型实时更新 递推算法,进而实现对特征退化分布和实时剩余寿命的不断实时更新;最后,采用IEEE PHM 2012的轴承全寿命数据对本文方法进行了验证,并与基于Gamma分布[23]的剩余寿命预测方法进行了比较,验证了本文预测方法的正确性和有效性。
1 核密度估计模型的构建
在实际应用中,随着现代传感技术的发展,越来越多的设备劣化状态可以直接或间接获得,研究者往往可以通过传感器监测到历史状态数据,选择能表征部件连续退化的特征量,以更好地揭示退化部件的真实状态,满足建模的需要。
设tk为当前监测时刻,[0,tk]的监测数据为当前接收到的设备退化数据,则相应设备特征可以随监测时间的退化趋势得到,如图1所示。设每单位时间采集一次随机退化特征增量的样本,ΔX1,ΔX2,…,ΔXk为k个抽样于[0,tk]的独立同分布的随机退化特征增量样本,将其服从的概率密度函数记为fk(Δx),则未知密度函数fk(Δx)的核密度估计可表示为
(1)
式中:k为已知的随机退化特征增量的样本数;hk为决定每个样本贡献度的平滑窗宽;K为核函数。样本ΔXi对密度估计的贡献度取决于核函数和所选择的窗宽,即在给定样本之后,核密度估计性能的好坏,取决于核函数K及窗宽hk的选取是否适当。

对于核密度估计与真实密度之间误差的测量方法有许多,积分均方误差(MISE)作为一种最易处理的全局测量方法被广泛使用。
(2)
Silverman[24]基于积分均方误差最小的思想,通过对不同核函数(Epanechnikov、高斯(Gauss)、三角(Triangle)等)的效率进行比较,认为不同核函数对积分均方误差的偏差影响非常小。这里选择实际中应用最为广泛的高斯核函数(Gaussian Kernel),用于核密度估计的模型。
(3)

(4)
将高斯核函数K(Δx)代入式(4),初始最优窗宽
(5)
式中σk为k个已知的初始随机退化特征增量样本的方差,
(6)

(7)
2 核密度估计模型的实时更新
2.1 自适应窗宽的确定及自适应窗宽下的核密度估计
由上述建模过程可以发现,假设初始窗宽hk为整个区间的固定窗宽,则随着动态监测系统时间的推移,当tk+1时刻获得新的退化特征增量数据ΔXk+1时,k+1个样本数据的固定窗宽核密度估计可表示为
(8)
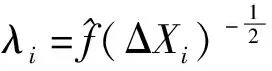
(9)
对于动态实时监测系统,当监测到第k+1个样本时,第k+1个样本数据点处的自适应窗宽可表示为
(10)

设ΔX1,ΔX2,…,ΔXk是来自未知密度函数f(Δx)的初始样本,当新增一个样本数据ΔXk+1时,未知密度函数f(Δx)基于自适应窗宽的核密度估计表示为:
(11)
式中h(ΔXi)(i=1,2,…,k+1)表示不同样本点处的自适应窗宽。
2.2 自适应核密度估计的实时更新
由于研究对象是实时监测系统,每监测到新的样本数据,进行核密度估计时都要重新计算,这就造成每新增一个样本数据,求新增样本后的核密度估计时,其所有历史样本的核密度估计也需要重复计算。随着样本数据的不断增多,计算量也会变得越来越大。为提高核密度估计模型的实效性,减少不必要的重复计算,通过ΔX1,ΔX2,…,ΔXk这k个初始历史样本的核密度估计递推得到k+1个样本,即监测到ΔX1,ΔX2,…,ΔXk,ΔXk+1时的核密度估计,从而实现核密度估计的实时更新。具体利用式(11)可得:
(12)
式中h(ΔXk+1)为样本点ΔXk+1处的的自适应窗宽值,由式(10)计算得出。
因此,当任意tk+j时刻新增j(j=1,2,3,…)个样本时,k+j个样本数据的核密度估计可通过递推得到:
j=1,2,3,…。
(13)
这样,实时监测过程中每新增一个退化特征增量样本,核密度估计都可以由其历史退化特征增量的样本自适应递推得到,从而可有效避免实时监测系统中的重复计算问题,提高核密度估计过程的效率。
3 特征退化分布的计算

(14)
当tk+1时刻新增一个样本时,[0,tk+1]特征退化量的概率密度函数可表示为:
(15)
当tk+j时刻新增j个样本时,[0,tk+j]时间累积退化量xk+j的概率密度函数可表示为:
j=1,2,3,…。
(16)
4 剩余寿命预测模型的建立
对于给定的失效阈值xth(设tk+t时刻累积退化量为xth时,系统失效),如图2所示。要实现剩余寿命的预测,首先要基于初始时刻到当前tk时刻的特征退化量X1:k(记Xk=X(tk),X1:k={X1,…,Xk}),预测tk+t时刻的特征退化量Xk+t。设每单位时间监测一次,增加一个新的样本数据,则tk+t时刻有k+t个样本数据。设T为设备在tk时刻的剩余寿命,则预测的剩余寿命的概率分布函数为
FT(t)=p(T≤t)=p(Xk+t≥xth)

(17)
式中g(xk+t)为[0,tk+t]特征退化量的概率密度,
(18)

将式(18)代入式(17),可将预测的剩余寿命的概率分布FT(t)通过换元积分法化为
(19)
根据不断更新的样本,将来tk+t时刻k+t个随机特征退化增量样本的自适应核密度估计可表示为
(20)
因此,[0,tk+t]特征累积退化量的概率密度为
(21)
将式(21)代入式(19),则tk时刻预测的设备剩余寿命T的概率密度函数为
(22)
在获得新的退化特征增量数据后,可以根据剩余寿命预测的概率分布函数FT(t),重新计算下一时刻的概率分布函数FT(t+1),从而实现对预测的剩余寿命分布的更新。
5 实例计算与分析
本文利用IEEE PHM2012提供的轴承全寿命数据对模型进行验证。该数据来源于FEMTO-ST研究中心PRONOSTIA试验台对滚动轴承的加速寿命试验,其中振动信号的采样频率为25.6 kHz,每次采样时长为0.1 s,采样间隔为10 s,即每次采样可得到2 560个样本数据。本文以转速为1 800 rpm,载荷为4 000 N工况下的Bearing 1-1的全寿命振动数据为例进行分析。
轴承故障诊断中,由于均方根(RMS)可以较好地反映轴承的磨损退化,在实际中得到了广泛应用。本文以Bearing 1-1的均方根特征随监测时间的退化趋势为例进行分析(如图3)。由图3可以看出,均方根随时间基本呈现单调增加的趋势,能较好地反映其退化趋势,该轴承在t=2.749×104s时磨损开始加剧,且在t=2.803×104s时失效,均方根的失效阈值为5.607 mm/s2。

5.1 基于固定窗宽与自适应窗宽剩余寿命预测准确性的比较
窗宽选择的好坏直接影响核密度估计的准确性。在实时剩余寿命预测中,退化特征增量样本随时间随机变化,如果窗宽在整个区间上取固定值,核密度估计时易造成样本数据少的地方拟合不足,而样本数据多的地方拟合过度;若根据样本数据的密度自适应地选择窗宽值,则高密度区域采用较大的核窗宽,低密度区域采用较小的核窗宽,可以更符合实际样本数据的需要,提高核密度估计的准确性,进而提高剩余寿命预测的准确性。
图4和图5所示为第2个监测点处(tk=1.7×104s)和第6个监测点处(tk=2.5×104s)基于固定窗宽与基于自适应窗宽剩余寿命(RUL)的概率密度(PDF)比较。

通过比较可以看出,基于自适应窗宽的剩余寿命预测结果相比较于基于固定窗宽的剩余寿命预测结果更接近实际的剩余寿命,且随着监测时间的增加、监测数据的增多,两种预测方法与实际剩余寿命之间的误差进一步减小,基于自适应窗宽的剩余寿命预测结果的误差相对更小,说明基于自适应的窗宽能够对概率密度进行更好地估计,从而能更准确地对剩余寿命进行预测。
5.2 基于核密度估计的实时剩余寿命预测
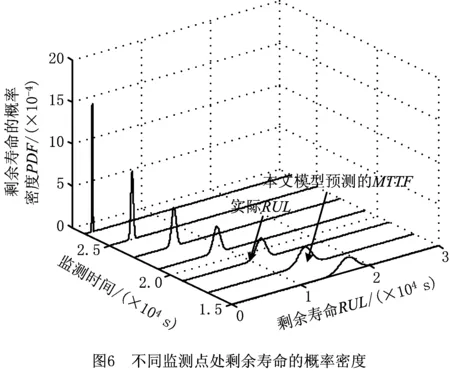
设以监测时间t∈[0,1.5]×104s单位时间随机退化特征(RMS)的增量作为初始样本,随着系统运行时间的增加,接收到的监测样本不断增多,基于核密度估计的剩余寿命的概率密度实时更新,剩余寿命的概率密度变窄变高,方差越来越小,说明预测的不确定性不断减小,如图6所示。此外,预测的剩余寿命值RUL越来越接近实际的剩余寿命值,其中,剩余寿命预测值通过平均剩余寿命(MTTF)[28]得到:

(23)
轴承的磨损过程是一个连续累积退化的过程,Gamma分布由于具有非负、增长、独立增量的属性,被广泛用于磨损和裂纹扩展等逐渐累积损伤过程的退化建模中。为进一步验证本文模型预测的有效性,对相同初始样本下相同监测点处的剩余寿命,采用基于Gamma分布的剩余寿命预测方法进行比较。图7和图8所示为在第1个监测点(tk=1.5×104s)和第7个监测点处(tk=2.7×104s)两种模型得到的预测剩余寿命的概率密度。由图7和图8的比较可以看出,本文模型预测的剩余寿命概率密度的方差相对于基于Gamma分布的预测模型有所变小,对退化数据拟合的程度更高,且到第7个监测点处时,本文方法预测的剩余寿命期望值已经很接近实际的剩余寿命值。


为进一步对本文所提方法的预测效果进行评估,对不同监测时间、实际剩余寿命、本文模型预测的平均剩余寿命以及基于Gamma分布预测的平均剩余寿命之间的比较,如表1所示。对比表中数据可以发现,随着监测时间的增加,监测信息不断增多,本文方法预测的剩余寿命值与基于Gamma分布的剩余寿命预测值相比,进一步减小,当监测到足够多的信息时,预测的剩余寿命逐渐变得很接近真实寿命,从而验证了本文基于核密度估计的实时剩余寿命预测模型用于剩余寿命预测的有效性。另外,通过两种模型预测所得剩余寿命与实际剩余寿命均方根误差(RMSE1,RMSE2)的比较也可以看出,随着监测时间的增加,RMSE1,RMSE2均呈现逐渐减小的趋势,且随着监测数据的增多,本文模型预测的结果与实际剩余寿命的误差更小,说明本文模型预测的剩余寿命值更接近实际的剩余寿命值。

表1 两种模型平均剩余寿命预测值(RUL)对比
6 结束语
在对许多机械设备剩余寿命预测时,很难得到大量破坏性试验样本数据,使得预测时采用传统的退化模型假设、参数估计方法结果往往不够准确的问题,本文提出一种基于核密度估计的实时剩余寿命预测方法,该方法不需要对数据分布的形式做任何假定,从数据本身出发研究数据分布特征。对于样本的核密度估计,针对传统的固定窗宽核密度估计会因样本的疏密程度不同导致拟合不足的问题,改进为自适应窗宽核密度估计,以提高拟合优度。此外,实时监测过程中,随着监测信息不断增加,针对核密度估计不断重复计算的问题,建立了核密度估计的实时更新模型。实例分析结果表明:随着实时监测信息的不断增多,预测剩余寿命的方差越来越小,预测准确度不断提高,并通过与基于Gamma分布的剩余寿命预测模型的结果比较,进一步验证了本文模型的有效性。可见,在不对退化数据分布做任何假设的前提下,该模型利用实时监测信息可以较准确地预测被监测设备的实时剩余寿命,从而可以为设备的实时预测维护提供有力的支撑,有效预防设备突然异常故障的发生,提高系统运行的安全性和可靠性。下一步,将在传统核密度估计用于实时剩余寿命预测的基础上,考虑随机变量的有界性对核密度估计的影响,并将改进的方法用于实时剩余寿命预测中。

