一种点接触粗糙表面摩擦行为的预估方法研究*
曹海龙,师俊平
(1.延安大学 建筑工程学院,陕西 延安 716000;2.西安理工大学 土木建筑工程学院,陕西 西安 710048)
0 引 言
随着机械零件的精密化发展,对于加工设备可靠性的要求越来越严格。其中,接触界面的接触特性是影响设备可靠性的关键因素之一。
目前,通过在接触界面间添加润滑剂,是提高接触界面接触特性的有效方式。而关于该类界面的研究主要包括粗糙表面和弹性流体动力润滑(EHL)两个方面:
一方面,国内外学者关于粗糙表面进行了大量的研究[1-2],其中,应用最多的是GREENWOOD和WILLIAMSON[3-4]提出的GW模型。GW模型是基于Hertz接触理论,将单个微凸体与弹性半空间的接触扩展到整个粗糙表面,获得了接触区域上的真实压力分布;李小彭等[5-6]基于分形理论将微凸体的变形分为弹性、弹塑性以及塑性变形,同时考虑了摩擦系数对连接界面接触刚度的影响。
另一方面,关于弹流动力润滑的研究主要包括线接触和点接触两方面。CHENG[7]首先针对连接界面间的弹性流体动力润滑开发了一种模型,该模型适用于分析微凸体为椭圆的Hertz接触;HAMROCK和DOWSON[8]对球轴承的EHL分析进行了全面的研究,结果显示,通过理论模型获得的结果与试验数据具有一致性;肖慧芳等[9]通过建立不同润滑状态下的滑动粗糙界面模型,研究了线接触滑动粗糙界面的动摩擦特性,获得了润滑状态下线接触粗糙表面的摩擦系数。为了精确预测接触中心的压力和油膜厚度,部分学者提出了采用多级求解器的方法计算接触中心油膜厚度。
上述关于弹性流体动力润滑的研究仅限于“平滑”的表面,忽略了表面粗糙度的影响。实际上,基于Hertz接触理论的两个球体之间的弹性接触,仅适用于光滑表面,而实际工程表面是粗糙的。ZHU和AI[10]给出了点接触EHL分析的数值解,同时研究了表面粗糙度对平均油膜厚度和接触压力峰值的影响;HU和ZHU[11]提出了一种简化的数值方法,用于点接触的EHL分析,该方法覆盖了所有润滑区域,包括全膜、混合和边界润滑;WANG等人[12-13]提出了一项考虑热效应的综合研究模型,该模型通过求解控制点接触润滑、弹性变形和热行为的方程组,来确定性地计算接触压力和表面温度,并在此基础上进行了点接触中粗糙表面之间滑动摩擦系数的模拟和测量;KRUPKA等[14]从光学干涉的角度出发,测量到了点接触粗糙表面的形状和压力分布。
需要指出的是,上述关于预测润滑状态下点接触的摩擦行为,一方面需要同时求解雷诺方程和流变方程,计算过程复杂且耗时;另一方面粗糙表面的微凸体高度分布均假设为高斯分布,没有对比分析微凸体高度分布为指数分布和三角分布的情况。
为了弥补以上的这些缺陷,笔者将基于JOHNSON等人提出的载荷分配思想,建立一种预测润滑点接触摩擦行为的模型,该模型不仅能够有效地降低模型的求解时间,还可以研究微凸体高度分布服从高斯分布、指数分布以及三角分布时,对连接界面摩擦行为的影响规律。
1 数值模型
1.1 摩擦模型
JOHNSON[15]认为润滑状态下,施加在连接界面处的总载荷由油膜压力和粗糙表面微凸体接触力组成,因此有:
FT=FH+FC
(1)
式中:FT—总载荷;FH—油膜压力;FC—粗糙表面微凸体接触力。
利用比例因子将式(1)替换如下:
(2)
式中:γ1—润滑油膜;γ2—微凸体的比例因子。
类似地,总摩擦力是两个分量的总和,即:
Ff=Ff,H+Ff,C
(3)
式中:Ff—总摩擦力;Ff,H—润滑油膜产生的摩擦力;Ff,C—微凸体接触摩擦力。
润滑油膜摩擦力可以表示为
Ff,H=τHdAH
(4)
式中:τH—流体剪切应力;AH—流体的接触面积。
微凸体接触摩擦力为:
(5)
式中:τCi—单个微凸体接触的剪切应力;ACi—单个微凸体的接触区域;N—接触的微凸体个数。
为简化计算,笔者将粗糙表面微凸体的摩擦力写为平均微凸体摩擦系数与微凸体接触力的乘积。因此,式(5)可以转化为:
Ff,C=fcFC
(6)
式中:fc—平均微凸体摩擦系数,为常数;FC—微凸体接触力。
为了确定润滑油膜的剪切应力,笔者采用BAIR和WINER[16]提出的有效粘度的定义,即:
(7)
其中:
(8)

τL通常被认为是压力的函数,因此可以表示为:
τL=τL0+β0pm
(9)
式中:τL0—极限剪切应力;β0—极限剪切应力-压力曲线的斜率;pm—Hertz接触的平均接触压力。
因此,单位面积的流体牵引力可以通过对剪切应力进行积分来确定,即:
(10)
假设两个粗糙表面的间隙是恒定的,且等于中心膜厚度,那么润滑油膜摩擦力可以写为:
(11)
式中:hc—中心膜厚;u—有效速度;a—点接触的半径。
根据Roelands[17]的公式,润滑剂粘度可表示为:
(12)
式中:η0—常温常压下入口区润滑剂的粘度;η∞=6.315×10-5Pa·s;cp=1.962×108Pa。
文献[18]中的参数Z为:
(13)
式中:α—压力-粘度指数。
联立式(3,6,11),可得总摩擦系数为:
(14)
1.2 弹流润滑模型
由式(12)可知,求解润滑油膜摩擦力需要先求解中心油膜厚度。NIJENBANNING等[19]基于雷诺方程、变形方程以及载荷平衡,对点接触粗糙表面的中心油膜厚度进行了估算,并获得了光滑表面点接触区的中心油膜厚度方程,即:
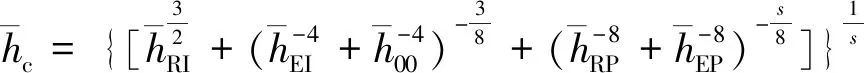
(15)
其中:
(16)
各无量纲参数分别为:
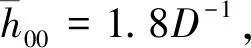
(17)
式中:RI—刚性-等粘性;RP—刚性-压电粘性;EI—弹性-等粘性;EP—弹性-压电粘性。
其他无量纲参数定义如下:
(18)
油膜厚度方程可以根据式(2,3)获得。
令pT=γ1pH,E′=E′/γ1,FT=FT/γ1,则通过式(15)可得混合润滑时点接触的中心膜厚度为:
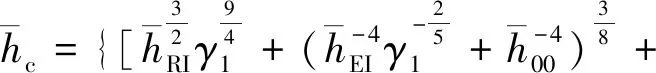
(19)
其中:
(20)
1.3 粗糙表面接触模型
粗糙表面的接触特性可由GREENWOOD和TRIPP提出的点接触模型来表征。
该模型将两粗糙表面间的接触简化为光滑球体与微凸体高度服从统计学分布的粗糙表面间的接触,且两个粗糙表面间的间距d可以表示为:
(21)
式中:R—球体的曲率半径;wb—基体位移;y(r)—球体的纵坐标;y0—接触中心的值。
基体位移wb可以写成:
(22)
式中:K(k)—第一类的完全椭圆积分,参数k=2(rs)1/2/(r+s)。
假设微凸体只发生弹性变形,则距离接触中心r处的有效压力为:
(23)
式中:zs—微凸体的高度;n—微凸体的个数;β—微凸体的曲率半径。
为了将粗糙表面的接触压力与点接触的最大Hertz压力值相关联,通过一系列的曲线拟合,可以获得如下表达式:
(24)
式(24)中的无量纲参数可以表示为:
(25)
(26)
式中:a=0.234 2;b=0.818 9;c=-0.272 0;p0—点接触的最大Hertz接触压力。
p0的表达式为:
(27)
同理,根据GREENWOOD和WILLIAMSON建立的GW模型可知,粗糙表面的接触压力pc为:
(28)
其中:
(29)
通常情况下,微凸体的高度分布可以假设为以下3种情况,分别为:
(1)高斯分布:
(30)
(2)指数分布:
φ(s)=e-s
(31)
(3)三角分布:
(32)
微凸体高度服从不同分布时的概率密度函数如图1所示。
由图1可知,三角分布与高斯分布关于s=0对称,而指数分布为单调递减函数。
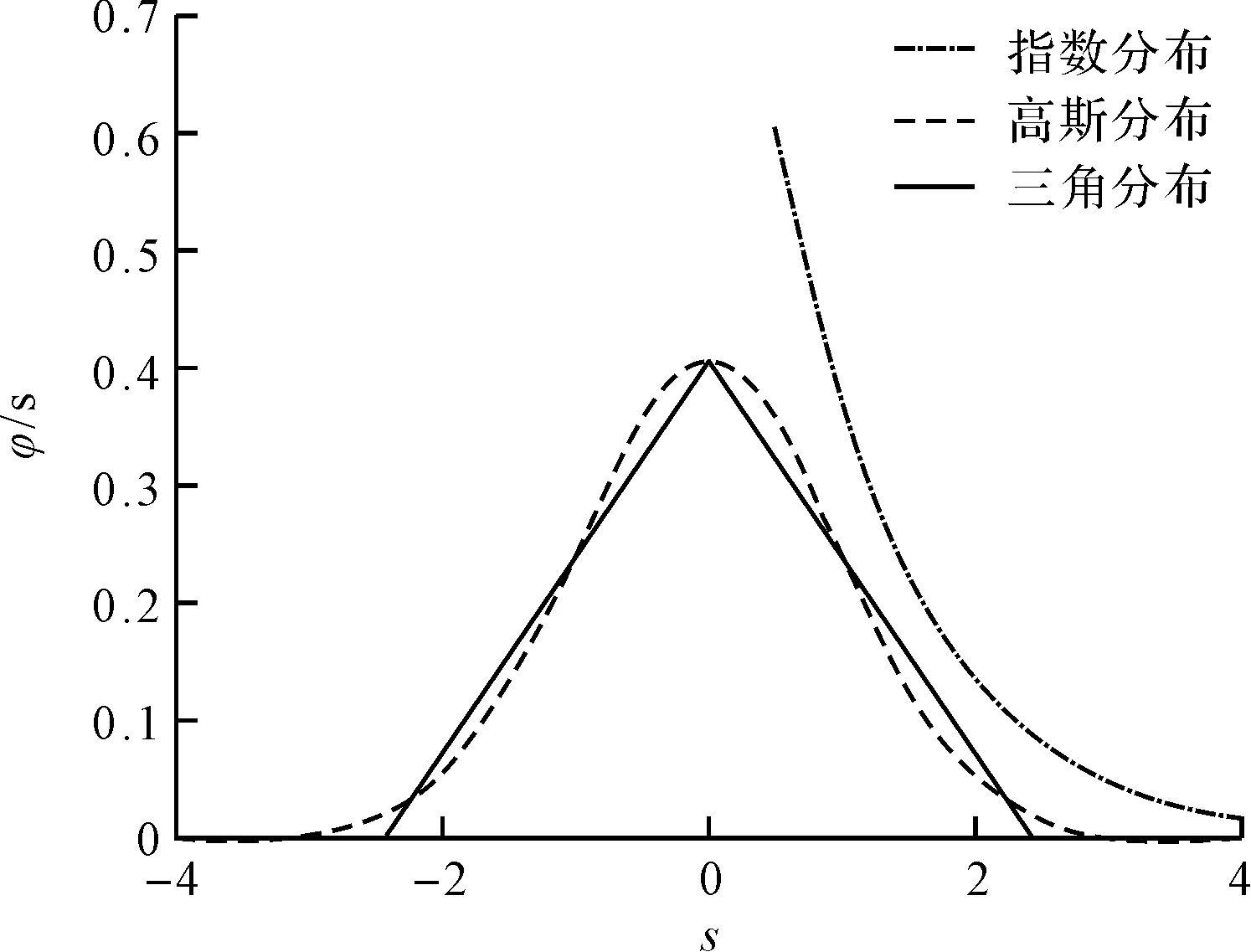
图1 三种分布函数曲线
为简化计算,令pT=γ2pC,E′=E′/γ2,FT=FT/γ2,n=nγ2,则联立式(24,27,28),可得:
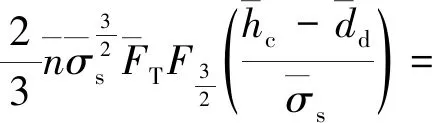
(33)
其中,无量纲参数为:

(34)
1.4 求解过程
本文采用迭代法联合求解非线性方程(2,19,33),求解流程图如图2所示。
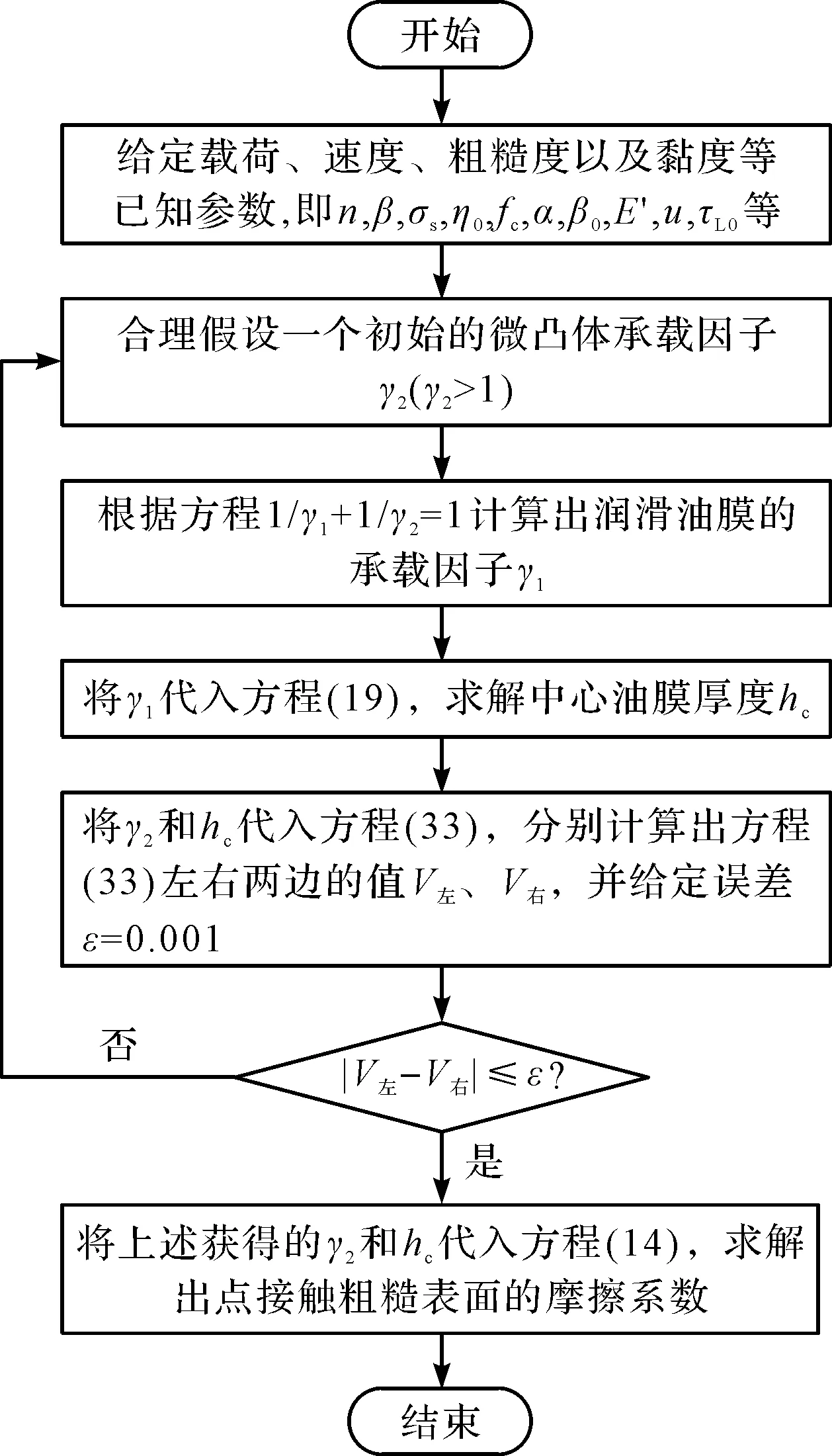
图2 数值求解流程图
假设D=1,并且Rx=Ry=R,则k=1,具体求解步骤如下:
(1)给定初始速度、法向载荷以及γ2,γ2>1;
(2)将给定的γ2代入方程1/γ1+1/γ2=1,即可求得润滑油膜的承载因子γ1;
(3)通过式(19)求解中心油膜厚度;
(4)将获得的中心油膜厚度代入方程(33)判断等式是否成立。若不成立,则继续迭代,直到两次连续迭代之间的误差低于指定的公差值εT=0.001;
(5)对下一个速度执行过程(1~4),直至获得所有速度对应的摩擦系数。
2 实验及结果分析
2.1 模型验证
为了验证新模型对摩擦系数预测的正确性,笔者使用WANG等人公布的试验结果。
文献中利用一个钢球与旋转的扁平样品进行了流体润滑试验,测试从低速开始,然后逐步增加,直到达到最大速度。在每个速度下,测试持续2 min以确保达到稳态条件。
模型中的输入参数如表1所示。
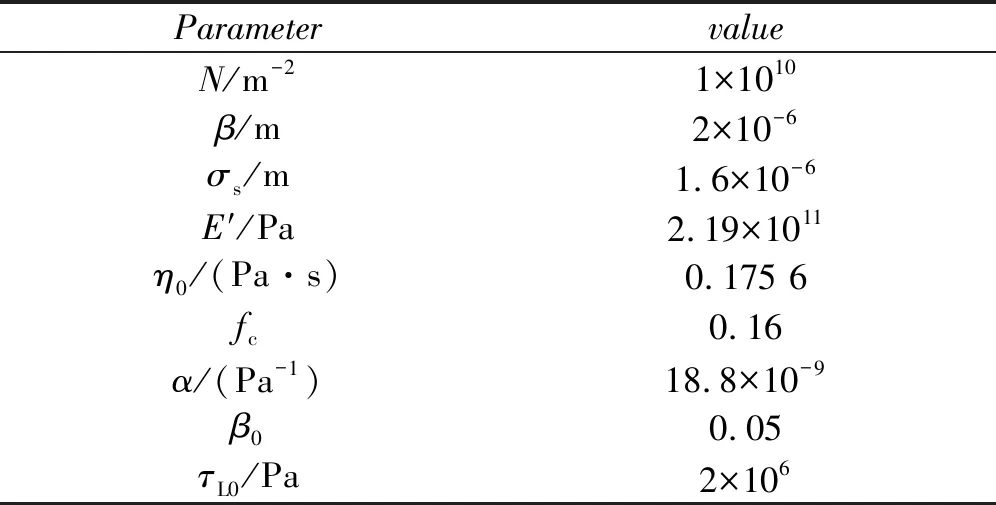
表1 模型输入参数
利用表1参数获得的仿真结果与试验结果的比较如图3所示。

图3 仿真结果与试验结果的比较
由图3可知:
仿真结果与文献中的试验结果具有一致性。该模型预测摩擦系数在边界润滑过程中基本保持不变,混合润滑状态下下降,从混合润滑状态转变为全膜润滑状态后略有增加。
但仿真结果与实验结果之间依然存在差异,而且当假设的微凸体高度分布为高斯分布和三角分布时,仿真的结果与试验结果间的误差较小;当假设的微凸体高度分布为指数分布时,模型预测的摩擦系数明显偏离试验结果。
2.2 载荷的影响
不同法向载荷下总摩擦系数随滑动速度的变化规律如图4所示。
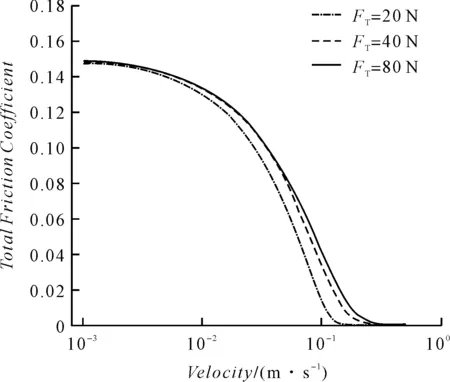
图4 不同载荷下总摩擦系数与滑动速度的关系
点接触情况通常发生在低载荷情况下,因此选取法向载荷分别为FT=20 N,FT=40 N,FT=80 N的3种载荷模拟表面的低载荷工况,其他参数与表1一致。
由图4可知:
在边界润滑状态时,载荷对摩擦系数的影响可以忽略不计,这主要是因为微凸体与微凸体的接触占主导地位,随着滑动速度的增加,润滑状态从边界润滑向混合润滑过渡,更多的流体参与到接触中,膜厚度增加,总摩擦系数逐渐降低;
此外,当滑动速度不变时,摩擦系数随着载荷的增加而增加;当滑动速度增加到临界值时,润滑状态从混合润滑过渡到全膜润滑,此时微凸体摩擦力减小,总摩擦力由流体动力摩擦主导。
2.3 粘度的影响
不同粘度对摩擦系数的影响规律如图5所示。

图5 不同黏度下总摩擦系数与滑动速度的关系
常见的润滑油粘度范围为1×10-3Pa·s~1 Pa·s。为便于分析,笔者选取润滑油粘度η0=0.001 Pa·s,η0=0.004 Pa·s,η0=0.008 Pa·s,分别表示粗糙表面间添加3种不同的润滑剂,其中,法向载荷FT=20 N,其他参数如表1所示。
显然,粘度的变化不会明显影响边界润滑状态下的总摩擦系数,因为摩擦系数在很大程度上受润滑剂化学成分的影响。混合润滑状态下,摩擦系数随着粘度的减小而增加,这是因为粘度越低,微凸体与微凸体接触的可能性越大;全润滑状态下,摩擦系数与粘度直接相关,粘度直接影响着润滑剂剪切应力的大小。
此外,当润滑剂的粘度较低时从混合润滑到全膜润滑的转变推迟了,即所需的滑动速度增加了。
2.4 表面粗糙度的影响
表面粗糙度有3个不同的参数:微凸体密度n,微凸体峰顶平均半径β,以及微凸体高度的标准差σs。可以通过研究不同的表面粗糙度,来预测总摩擦系数的行为。通过对不同粗糙度参数的研究表明,微凸体高度标准差σs的变化对摩擦系数的预测有显著影响。
不同表面粗糙度对摩擦系数的影响规律如图6所示。
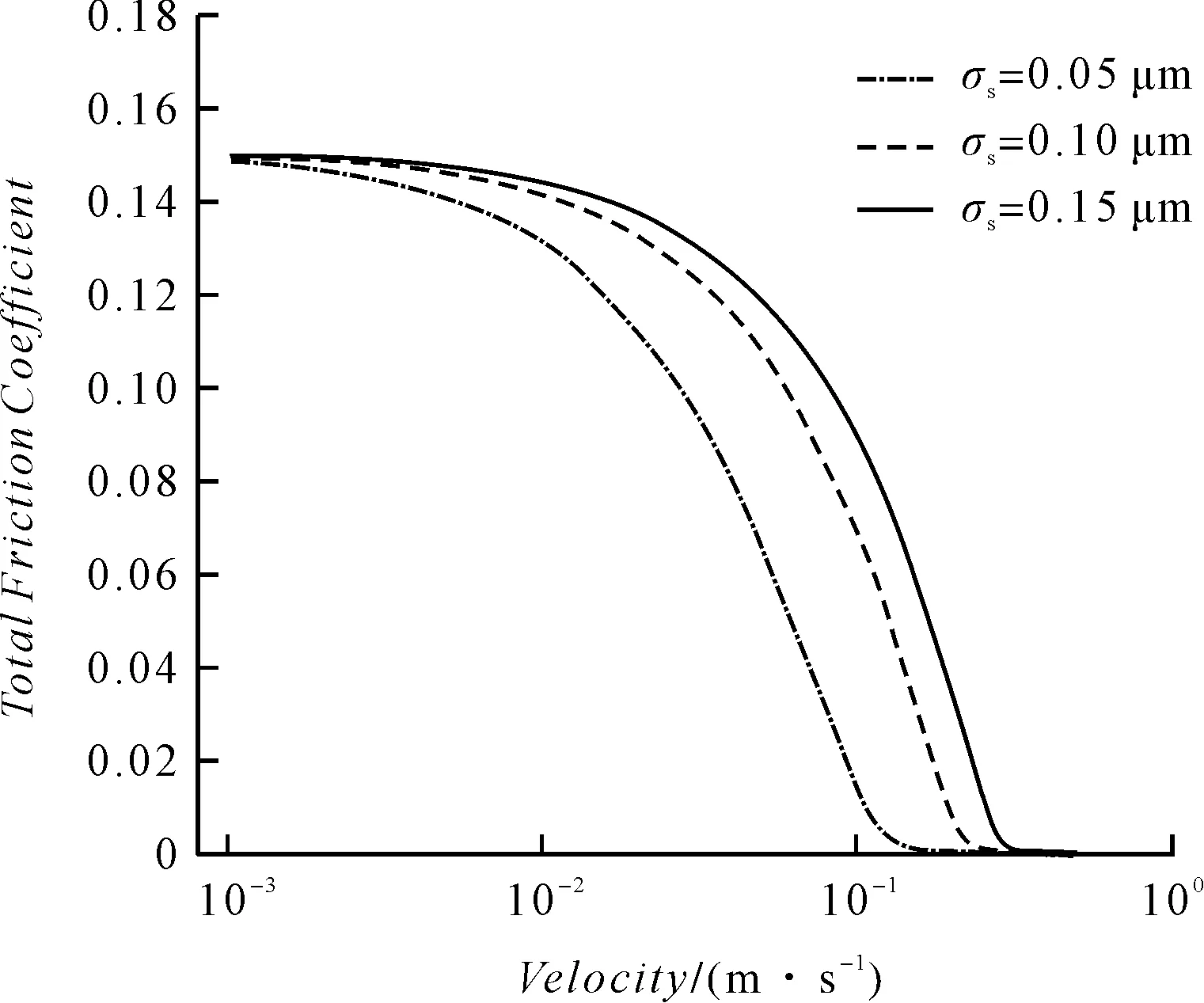
图6 不同表面粗糙度下总摩擦系数与滑动速度的关系
与图(4,5)类似,法向载荷FT=20 N,σs=0.5×10-7m,σs=1×10-7m,σs=1.5×10-7m分别表示3种不同的粗糙表面,其他参数如表1所示。
由图6可知:
当滑动速度一定时,随着表面粗糙度的增加,总摩擦系数增加,从混合润滑状态到全润滑状态所需的滑动速度增加。这是因为表面越粗糙,填充微凸体间的间隙所需的膜厚度越大,导致越多的微凸体间的接触。
3 结束语
基于JOHNSON等人的载荷分配思想,笔者提出了一种点接触粗糙表面摩擦行为的预估方法;润滑状态下连接界面的法向载荷和摩擦力由粗糙表面和流体动力油膜共同承担,利用Hertz理论中的最大接触压力确定了粗糙表面的接触载荷,通过弹性流体动力润滑膜厚公式求解了流体动力油膜承担的载荷。
研究结果表明:仿真结果与试验结果具有一致性,表明该方法是有效的;且法向载荷、润滑剂粘度、表面粗糙度以及假设的微凸体高度分布是影响摩擦系数的关键因素。
在实际工程中,可以通过增加载荷和降低粘度的方式提高摩擦系数,同时也可以通过改善工件表面粗糙度的方式来降低其摩擦系数。

