气浮轴承均压腔内圆角结构对振动特性影响的实验研究*
武 静,钱俊兵,袁锐波*
(1.昆明理工大学 机电工程学院,云南 昆明 650500;2.昆明理工大学 民航与航空学院,云南 昆明 650500)
0 引 言
因具有低摩擦、低功耗、高精密、无污染等优点,气浮轴承被广泛应用于半导体、超精密测试设备和高精密加工机床设备等领域[1-2]。然而随着设备精度的要求不断提高,气浮轴承的微振动制约着其运动定位精度的进一步提升,使制造加工精度无法更高。
为研究自激振动的起因和抑制方法,国内外学者做了大量研究。KAWAI等[3]认为是由于结构中微观粗糙表面诱发气体湍流而引起的自激微振动;SAWADA等[4]对气浮导轨的性能进行了分析,发现了导轨结构对振动的影响;AL-BENDER等[5]总结了描述气浮轴承压力气膜的各种方法,提出了主动补偿措施提高轴承稳定性;CHEN等[6]提出了有腔小孔节流气浮轴承在节流孔出口处存在气旋,并提出了气旋会引起气膜振动的观点,对比了多种气腔内的气体流动特性,提出了球形腔结构能有效抑制气浮轴承的微振动的观点;李运堂等[7]运用了LES方法分析了小孔节流气浮轴承内的气体流动特性,研究证实了气浮轴承发生自激振动主要是气旋的产生和破裂;陈琦等[8]提出了在气浮轴承工作表面增加均压槽的方法来抑制轴承的微振动;杜建军等[9]以圆周方向有均压槽的气浮轴承为研究对象,分析得到了气锤振动稳定的判别方程;龙威等[10-11]分析了轴承内部气膜波动形成机理,发现了气膜流场内气旋分布规律与轴承微振动有着密切关系,并通过实验得到了沿气膜高度方向的振动是导致气浮轴承微振动的主要因素的结论;薛义璇等[12]通过仿真分析发现了气浮轴承气腔带倒角的结构能提高轴承的稳定性。
综上所述,虽然对于气浮轴承微振动特性的研究一直是关注热点,很多学者也分析了它的形成机理,但目前还没有关于均压腔内圆角结构对气膜振动特性影响的实验研究。
本文将通过设计实验方案,采集气浮轴承气膜的振动数据,分析均压腔内圆角结构对气膜振动特性的影响,为超精密静压气浮轴承的设计提供一定的参考。
1 气浮轴承实验
气浮轴承的工作原理示意图如图1所示。
图1中,高压空气经进气道进入节流孔小孔节流后,进入均压腔环面二次节流,再进入轴承底部与支承平台形成的微小间隙(即气膜间隙)向周边扩散,最后经过轴承边缘排出大气。
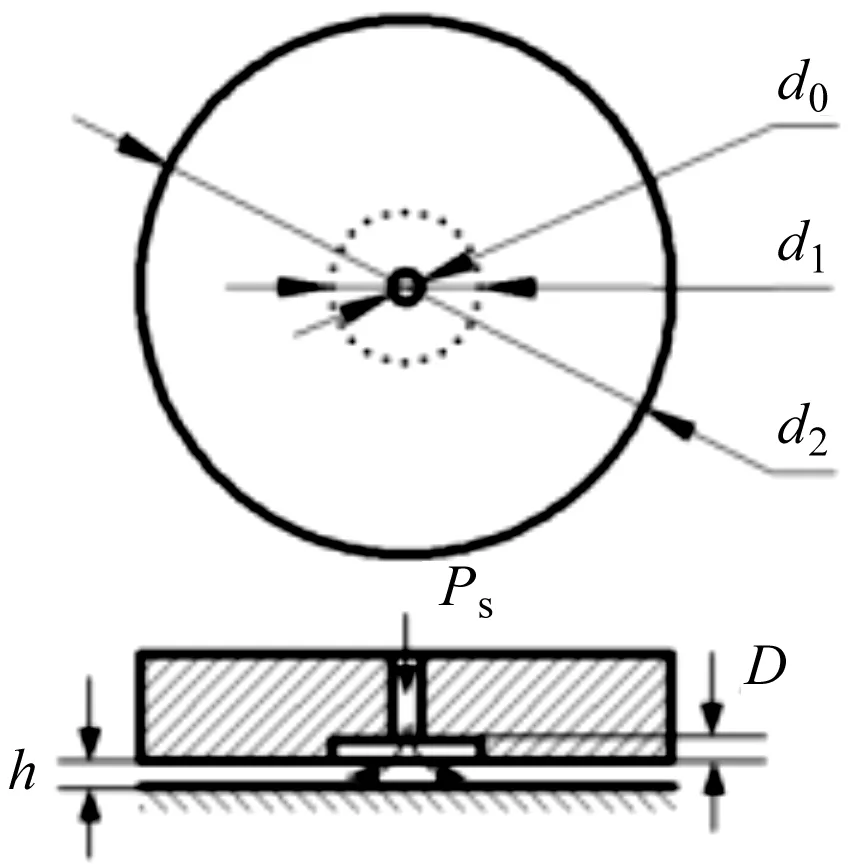
图1 气浮轴承工作原理示意图
由于气膜间隙十分微小,间隙内的压力始终大于大气压力,气膜具有一定承载能力。
1.1 实验原理和装置
为了实现对气浮轴承微振动信号的测量,笔者研究其振动特性。
具体是将气浮轴承作为测试对象,供气孔与轴承气道连通,通过电感测微仪实时测量气膜厚度,加载气缸压力改变气膜厚度,将气膜间隙控制在10 μm,再通过LMS动态检测仪将加速度传感器采集到的振动型号传输到PC端。
气膜微振动实验原理图如图2所示。
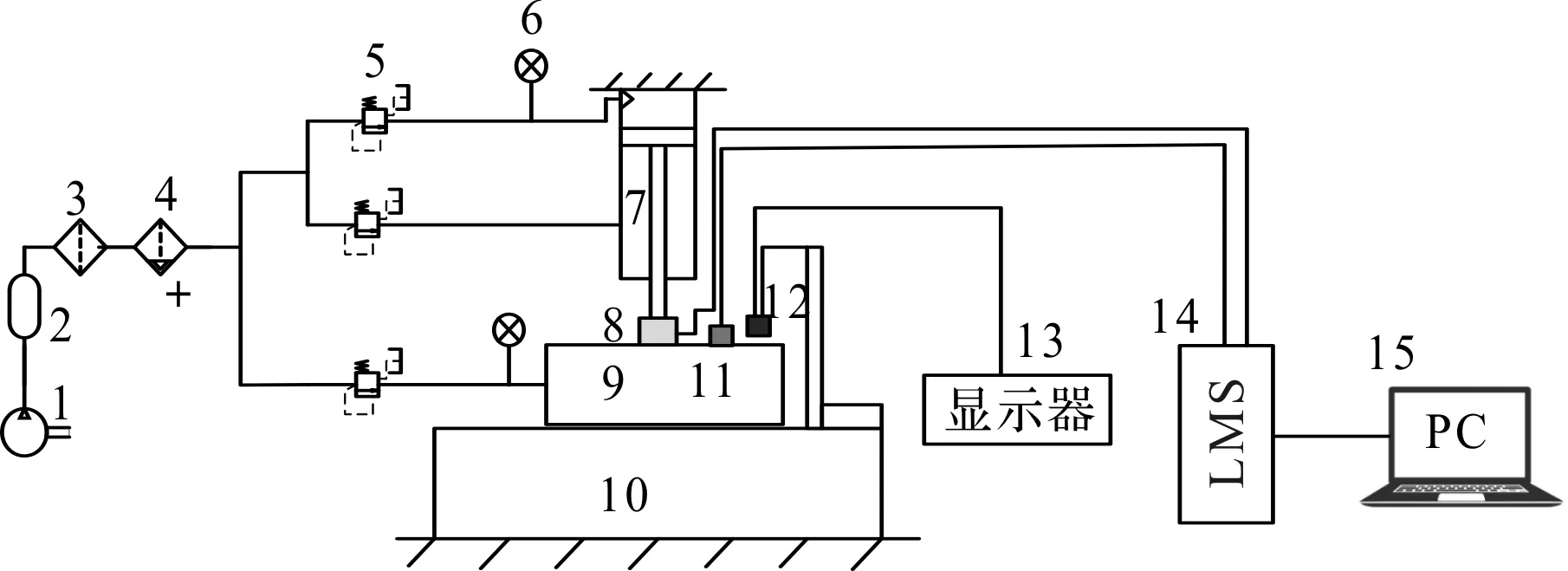
图2 气膜振动测试实验原理图1—空压机;2—气罐;3—过滤装置;4—油雾分离器;5—减压阀;6—压力表;7—气缸;8—动态力传感器;9—气浮轴承;10—大理石隔振平台;11—加速度传感器;12—电感测微仪;13—电感微位移显示器;14—LMS动态监测仪;15—计算机
在整个实验中,由空压机提供气源。其中:
过滤调压阀的型号为SMC AW30-03D-A,油雾分离器的型号为SMC AFM30-03D-A;
减压阀的型号为SMC IR2020-02,其设定压力范围为0.01 MPa~0.8 MPa;
气缸的型号为SC63X,满足使用压力范围(0.1 MPa~1.0 MPa);
动态力传感器的型号为BSHS-1(量程0~150 kg);
PCB加速度传感器型号为352A24 SN LW195334;
LMS动态监测仪进行振动数据的实时采集和记录,频率采集范围为0~40 MHz,扫描精度±2%。
电感测微仪为DGC-8ZG/D型微位移传感器,其分辨率为0.01 μm,显示误差在±0.05 μm;电感微位移显示器的型号为DGS-6C。
微振动测试装置实物图如图3所示。

图3 微振动测试装置实物图
1.2 实验条件与方法
为了研究均压腔内圆角结构对轴承振动特性的影响,笔者设计了不同节流结构的气浮轴承。
节流方案局部图如表1所示。
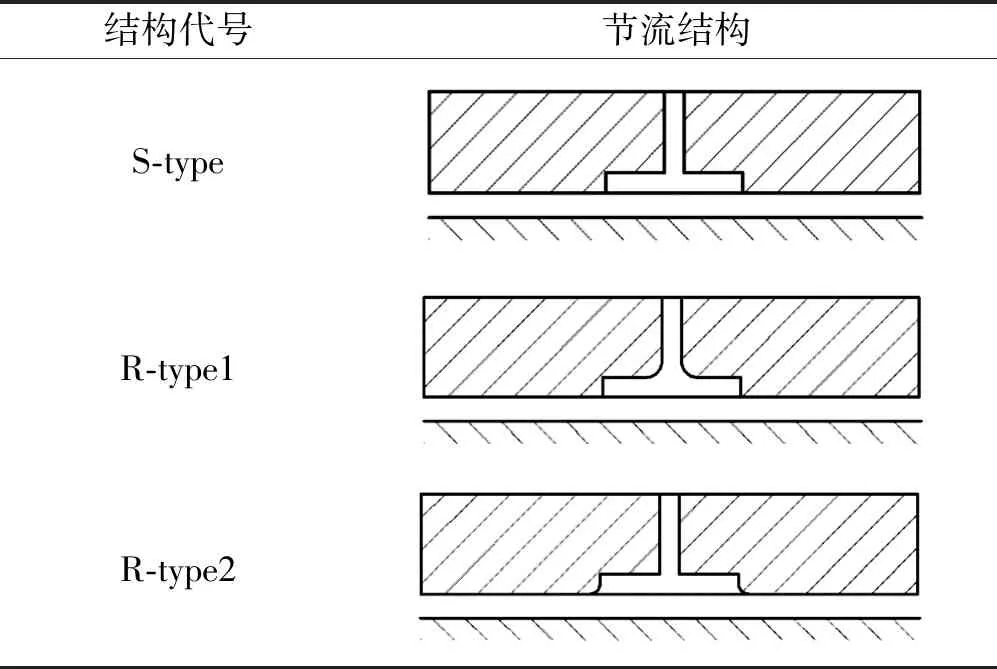
表1 节流结构方案局部图
表1中,笔者以均压腔无圆角连接的小孔节流气浮轴承(S-type结构)、节流孔出口(即均压腔入口)处圆角连接的气浮轴承(R-type1结构)和均压腔出口圆角连接的气浮轴承(R-type2结构)3种结构的气浮轴承为实验对象。
其中,节流孔直径d0=0.15 mm,均压腔直径d1=6 mm,轴承直径d2=60 mm,均压腔深度D=0.1 mm。
其中,R-type1和R-type2结构中圆角结构为半径R=0.05 mm的圆弧。
实验环境温度为25 ℃;轴承供气压力Ps为0.2 MPa~0.6 MPa。适当加载气缸压力,使气膜间隙厚度保持在h=10 μm。
本文对保持气膜间隙稳定后的S-type结构、R-type1结构和R-type2结构的气浮轴承进行振动测试,使用LMS动态检测仪采集其振动数据,经过多次测量比较,保证数据的准确性。
2 数学模型
气浮轴承节流孔和均压腔内气体是复杂的湍流运动,均压腔内的气旋导致气膜内气体流速的改变,由于壁面剪切作用与气体流速的变化,使得节流孔出口处产生气旋涡,而在远离节流孔出口处会产生气旋涡的破裂或分解。
由气体静压润滑理论可知,气浮轴承内气体流场的连续性方程可以用Navier-Stokes(N-S)方程[13]表示,即:
(1)
式中:p—气体压强;μ—气体动力粘度;u—x方向上的速度分;v—y方向上的速度分量;w—z方向上的速度分量;ρ—气体密度。
根据气体为定常流动,以及气膜区域内部沿气膜厚度方向压力p与z坐标无关等条件,可以得到气体在气膜间隙内流动的简化气体的动量方程式[14],即:
(2)
当模型结构发生改变时,轴承内部的边界也随之改变,此时常用的N-S方程将不能很好地表达出轴承边界气体滑移流动特性和内部压力分布特征;根据广义Maxwell速度滑移边界理论,此时需要添加速度滑移边界条件[15-16],即为:

(3)
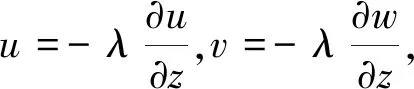
(4)
式中:λ—边界滑移长度;h—为气膜高度;U—轴承气膜的表面速度。
当轴承结构改变时,边界滑移长度λ也随之改变,直接影响速度分量u、v、w的大小。且由式(4)可知,λ对竖直方向的速度分量w影响最大。
在有腔小孔节流气浮轴承中,均压腔内气旋的变化是引起轴承微振动的主要因素,而气旋的变化是由腔内流体的速度变化而引起的,即可以通过改变边界条件来削减轴承的振动强度。
所以笔者通过改变边界条件,即改变轴承结构的方法来探究削减轴承微振动的措施。
3 实验结果及分析
在静态稳定工作条件下,为研究S-type、R-type1和R-type2结构的气浮轴承内部气膜的振动特性,笔者设计了实验方案,采集了3种不同结构气浮轴承的振动信号,分析了3种结构在不同供气压力的微振动幅值及频域特性的变化规律,对比分析了均压腔内圆角结构及圆角位置对振动特性的影响。
由于相比沿气膜平面竖直方向,沿气膜平面半径方向的微振动的影响较小,笔者主要研究沿竖直方向的微振动幅值及频域变化。
3.1 时域分析
通过实验可以读取10 s内轴承的振动幅值变化的平均值,在供气压力0.2 MPa~0.6 MPa时,笔者分别记录3种结构的气浮轴承的振动幅值,绘制出的不同供气压力下的振动幅值变化,如图4所示。

图4 不同供气压力下的振动幅值变化曲线
从图4可以看出:
(1)当供气压力由0.2 MPa增加至0.6 MPa时,S-type结构的振动幅值A从3×10-3g增加至12×10-3g;R-type1结构的振动幅值A从3.5×10-3g增加至9×10-3g;R-type2结构的振动幅值A从4.0×10-3g增加至9×10-3g;
(2)随着供气压力增大,3种结构的气浮轴承沿气膜平面竖直方向的微振动幅值也随之增大,即气浮轴承的微振动强度随着供气压力的增大而增大;
(3)当供气压力小于0.3 MPa时,S-type结构的微振动强度(3×10-3g~4.5×10-3g)小于R-type1结构(3.5×10-3g~4.5×10-3g)和R-type2结构(4×10-3g~6×10-3g)的微振动强度;
(4)当供气压力大于0.3 MPa后,S-type结构的微振动强度随着供气压力的增大,大幅增加由4.5×10-3g增加至12×10-3g,R-type1结构和R-type2结构的微振动强度分别由4.5×10-3g和6×10-3g增加至9×10-3g。
由此可以明显看出:R-type1结构和R-type2结构能减缓由于供气压力增大而导致轴承微振动的增强。
这是由于:
(1)当供气压力低(Ps≤0.3 MPa)时,气膜间隙内的气流速度较低,产生的气旋强度较弱,此时的振动大部分是由气浮轴承结构和实验平台共振所引起的;
(2)当采用较高供气压力(Ps≥0.4 MPa)时,轴承气膜间隙内气流所携带的能量也较大,此时由气膜内气旋运动而引起的振动也不容忽视,但是R-type1结构和R-type2结构均压腔内存在圆角连接,可以起到过渡引流的作用,在一定程度缓解了节流孔出口处或均压腔出口处由于气体流动横截面积的扩大,而导致气体急剧变化引起的轴承振动。
综上所述,均压腔内圆角结构的存在能减缓因供气压力过大而引起的轴承微振动,即在高压环境下,均压腔内采用圆角连接结构的气浮轴承的稳定性优于没有采用圆角连接结构的轴承。
3.2 频域分析
实验完成后,提取轴承振动的频域信号。
在不同供气压力下,笔者研究的3种结构的气浮轴承的频域信号如图5所示。

图5 不同供气压力下的频域信号
其峰值频率如表2所示。

表2 3种结构峰的值频率对比表
从图5和表2可以看出:在相同气膜厚度(h=10 μm)时,同一结构的气浮轴承的微振动有着相似的频率特征,随着供气压力的增大,微振动强度也在增大,但产生峰值的几个频率点基本是重合的。
对于不同结构的气浮轴承,虽然产生的峰值的频率点不一致,但产生最大峰值的主频段基本都在4 kHz附近,具体情况为:
(1)对于S-type结构,峰值频率主要集中在0.98 kHz、3.8 kHz、5.3 kHz、19.8 kHz等一系列频段内,振动幅值最大处即主频段在3.8 kHz频段处;
(2)对于R-type1结构,峰值频率主要集中在0.63 kHz、2.0 kHz、4.1 kHz、19.3 kHz等一系列频段内,主频段在4.1 kHz频段处;
(3)对于R-type2结构,峰值频率主要集中在0.75 kHz、1.8 kHz、3.5 kHz、19.9 kHz等一系列频段内,主频段在3.5 kHz频段处。
虽然对于R-type1结构和R-type2结构,在20 kHz频段内振动幅值有一定增长,但其增长幅值较小,也不易产生共振。
上述实验结果表明:随着供气压力的增大,会使轴承内部的微振动强度增强,而均压腔内圆角连接的结构能减缓气流与轴承壁面的冲击,虽会使高频段的振幅有些许增大,但抑制了主频段内的幅值增长,从而降低了气膜内的振动强度。
4 结束语
通过搭建相关实验平台,笔者采集了传统有腔小孔节流气浮轴承(S-type结构)和均压腔内圆角连接结构的气浮轴承(R-type1结构和R-type2结构)的振动信号,对比分析了其时域信号和频域信号,并得到了以下主要结论:
(1)分别对比均压腔内无圆角结构、节流孔出口圆角连接结构和均压腔出口圆角连接结构的时域信号可知,随着供气压力的增大,三者的振动强度都增大,但节流孔出口圆角连接结构和均压腔出口圆角连接结构的振幅增长较小,且当供气压力超过某定值时其振动幅值趋于平稳,即均压腔内圆角连接结构能有效削减因供气压力增大而导致的振动;
(2)对比均压腔内无圆角结构、节流孔出口圆角连接结构和均压腔出口圆角连接结构的频域信号可知,虽然三者结构产生峰值的频率点不一致但产生最大峰值的主频段都在4 kHz附近,即均压腔内圆角连接结构对振动的共振频率影响较小,对振动幅值的影响更大;
(3)对比节流孔出口处圆角连接结构和均压腔出口圆角连接结构可知,当供气压力超过0.5 MPa时,两种结构的振幅基本一致,即当高压工作时均压腔内圆角位置对振动的影响很弱;当供气压力低于0.5 MPa时,节流孔出口处圆角连接结构的振动强度较低,即节流孔出口圆角连接结构削减振动的效果更佳。

