含齿根裂纹故障的平行轴齿轮箱动力学特性研究*
任学平,武海锋
(内蒙古科技大学 机械工程学院,内蒙古 包头 014010)
0 引 言
当齿轮出现齿根裂纹时,其轮齿刚度会减小,在齿轮啮合过程中会引起异常振动,同时也会导致整个系统的动力学响应发生变化。齿轮作为传递速度和扭矩的重要零部件,其健康与否对齿轮箱的正常运行有着重要的影响。因此,通过动力学研究分析其力学的变化特性,从而提前预防裂纹扩展致使齿轮箱内部严重受损具有十分重要的研究意义。
建立良好的齿轮刚度及齿轮传动结构的数学模型可以精确地模拟实际工况下齿轮箱的运行状态。在以往计算齿轮啮合刚度时对不同齿数时齿根圆与基圆大小的关系考虑较少,导致计算结果有一定误差[1-2];且将齿轮的变形部分简化为轮齿部分,但未充分考虑轮体的变形。目前国内外的研究大多是基于刚体动力学仿真的基础上对其进行刚性动力学分析,但在对不同程度裂纹仿真的动力学响应研究中,并不能满足现有研究需要。
本文基于动力学仿真软件对带有齿根裂纹的故障进行分析研究,通过建立齿轮传动系统的扭转振动模型,利用ADAMS仿真得到的结果数据进行联合分析,最终得到结论,以期能够为平行轴齿轮箱故障诊断提供有力的理论依据和技术支持。
1 基于能量法的齿轮副啮合综合刚度算法
在最初的齿轮刚度能量算法中,考虑了对应的剪切刚度,但仍将轮齿部分视为非均匀悬臂梁;后来在此基础上充分考虑了轮体形变,即将非均匀悬臂梁的长度扩大到整个齿轮尺寸的二分之一,但未对轮体基圆与齿根圆的关系进行充分思考,导致对轮体均按基圆尺寸计算时,对于大齿数齿轮刚度计算结果误差较大。
根据机械设计手册可知,标准齿轮基圆半径与齿根圆半径计算公式分别为:
(1)
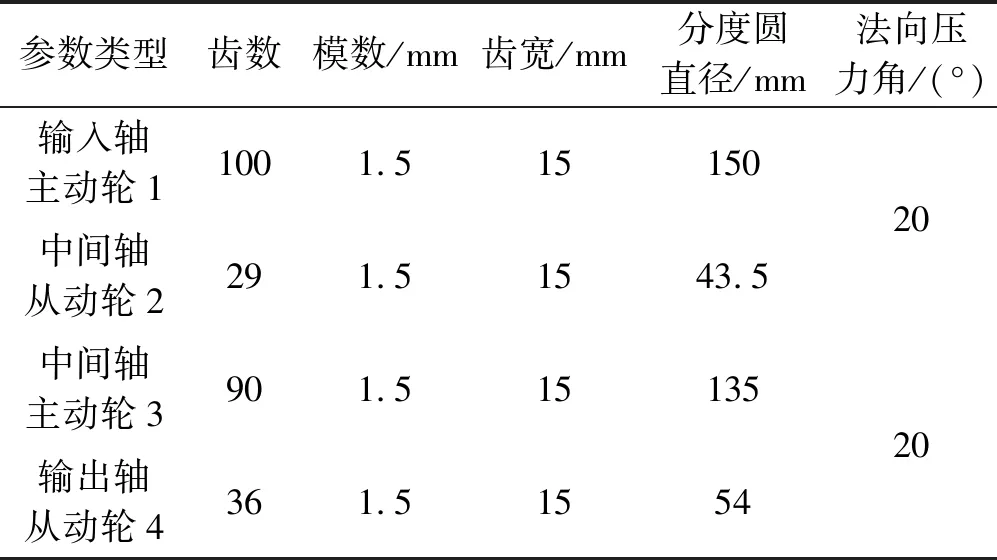
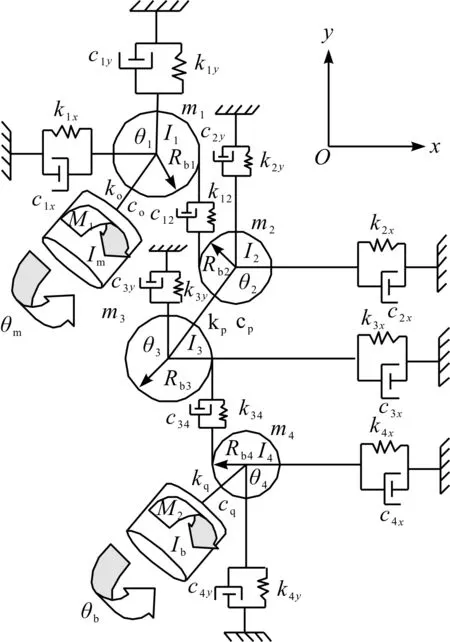
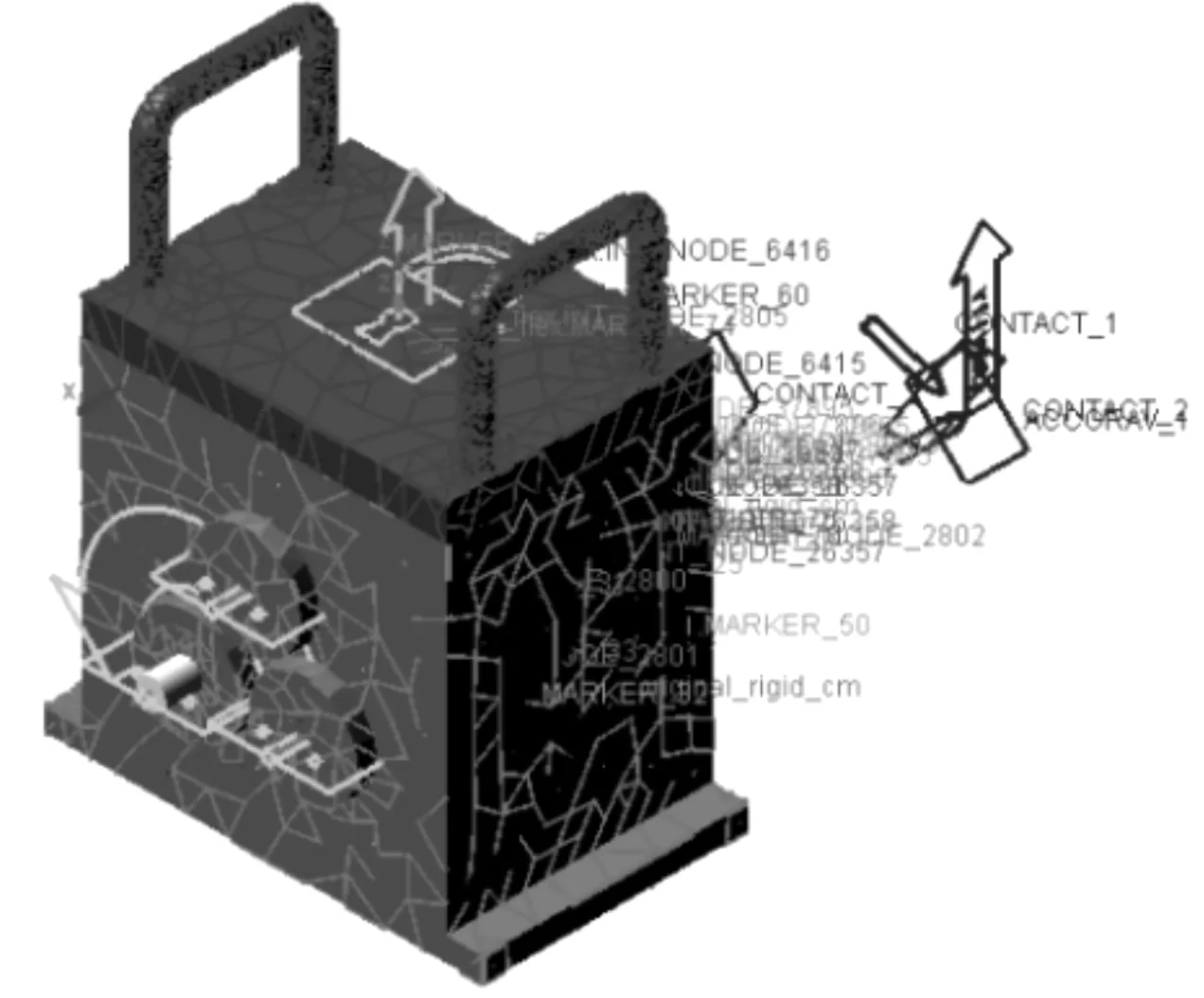
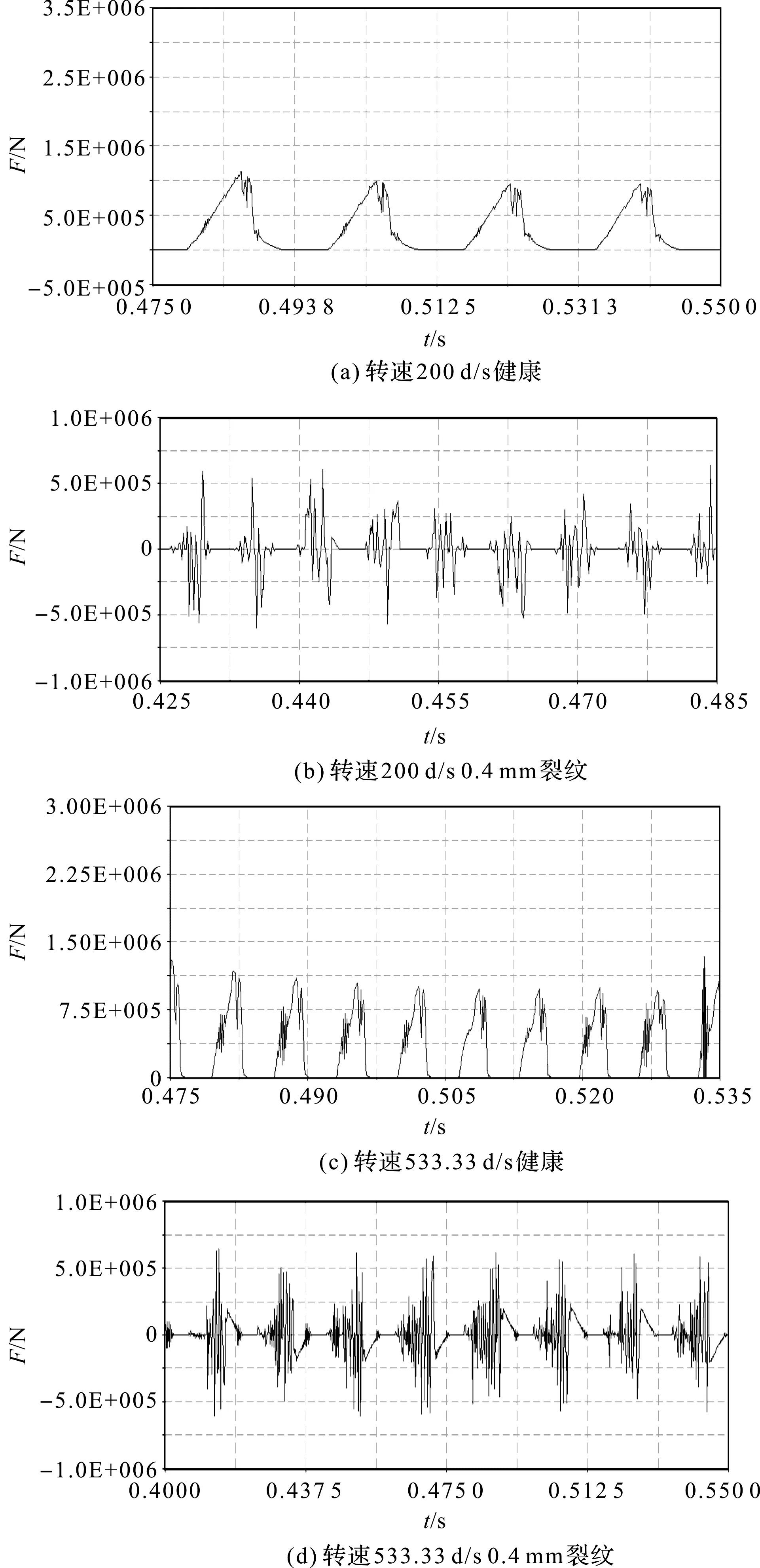
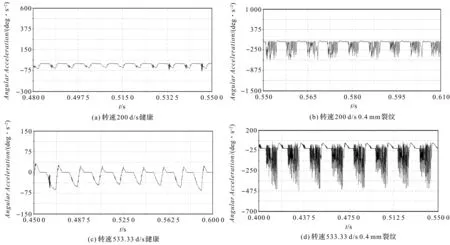
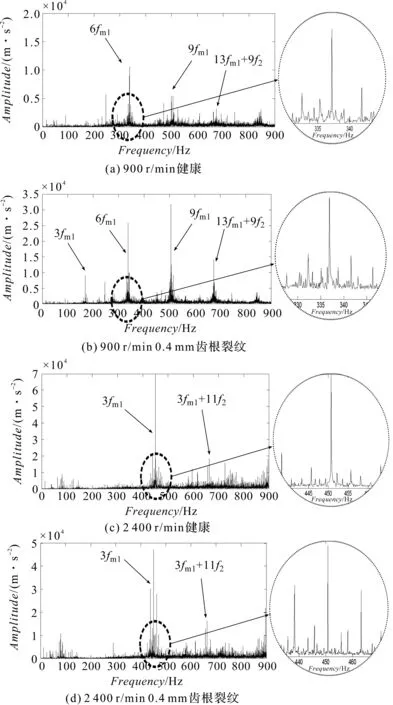
当Rb=Rf,z=41.45,对z取整为42。当z<42时,Rb>Rf;当z>42时,Rb 笔者以圆柱直齿轮为研究对象,根据材料力学法将齿轮简化成悬臂梁,如图1所示。 图1 齿轮简化悬臂梁示意图 根据图1可得,齿轮啮合过程的弯曲刚度、轴向压缩刚度、剪切刚度、赫兹接触刚度[3-5]分别为: (2) (3) (4) (5) (6) 式中:E—弹性模量;W—齿宽;ν—泊松比。 根据实际的齿轮箱齿轮材料信息可知:弹性模量E=2.06 E+11 N/m2;泊松比ν=0.3;齿轮材料密度ρ=7 800 kg/m3。 由图1的齿轮简化悬臂梁示意图可知,在齿轮健康状态下,距离齿根距离为x的断面横截面积Ax和面惯性矩Ix为: (7) (8) 对于含齿根裂纹的齿轮,断面横截面积Ax和面惯性矩Ix为: (9) (10) 最后,综合考虑轮齿的弯曲刚度、剪切刚度、径向压缩刚度以及轮齿的接触刚度,可得单双齿啮合刚度计算公式为: (11) 本文以DDS动力传动故障诊断综合实验台中的平行轴齿轮箱为分析对象,将健康齿轮和有齿根裂纹故障齿轮的啮合刚度MATLAB算法作为子程序,添加到DDS平行轴齿轮箱传动系统动力学程序中,进行下一步分析。 DDS平行轴齿轮箱齿轮传动系统相关参数,如表1所示。 表1 平行轴齿轮箱齿轮相关参数 笔者参照Bartelmus的扭转振动模型,建立了DDS平行轴齿轮箱的双参数(刚度和阻尼)扭转振动模型[6-10];将模型简化成为一个六自由度系统,通过建立传动系统的扭转和纵向振动系统方程(且包含驱动力矩M1和负载力矩M2),来分析齿根裂纹对系统振动的影响。 所建立的DDS平行轴齿轮箱传动系统数学模型如图2所示。 图2 DDS平行轴齿轮箱传动系统 传动系统扭转方程为: (12) 传动系统振动方程为: (13) 式中:Im—电机输入轴转动惯量,kg·m2(28.7 kg·m2);Ib—负载输出轴转动惯量,kg·m2(16.2 kg·m2);k12—1、2齿轮综合啮合刚度,N/m;k34—3、4齿轮综合啮合刚度,N/m;ko—输入轴扭转刚度(1.0×102N·m/(゜)),N·m/rad;kp—中间轴扭转刚度,N·m/rad(1.0×102N·mm/(゜));kq—输出轴扭转刚度,N·m/rad(1.0×102N·m/(゜));c12—1、2齿轮综合啮合阻尼,N·s/m(0.12k12);c34—3、4齿轮综合啮合阻尼,N·s/m(0.15k34);co—输入轴扭转阻尼,N·s/m(4.4×104N·s/m);cp—中间轴扭转阻尼,N·s/m(4.4×104N·s/m);cq—输出轴扭转阻尼,N·s/m(4.4×104N·s/m);M1—输入轴转矩,N·mm;M2—输出轴转矩,N·mm(10 N·mm)。 传统的建模处理方式是将齿轮箱中的齿轮和箱体当作刚性体来分析,但需要考虑齿轮啮合以及箱体端盖处振动过程中弹性变形,必须将齿轮及箱体模型进行柔性化处理,这样才能确保模型动力学分析的准确性与实用性。 本文采用SolidWorks建立齿轮箱的三维结构模型,并导入到ADAMS中;将齿轮2及箱体在ANSYS中柔性化导入到ADAMS中。 具体步骤如下: (1)在ADAMS中导入通过SoildWorks创建的平行轴齿轮箱Parasoild.x_t格式的刚性模型; (2)在ADAMS中将齿轮2及箱体导入到ANSYS进行柔性化处理,生成对应的mnf文件; (3)在ADAMS中通过柔性体替换完成平行轴齿轮箱的刚柔耦合模型的建立[11-13]; (4)在建立好的刚柔耦合模型中添加相应的约束:各个轴端施加旋转副,刚体齿轮和轴通过质心施加固定副,柔性体齿轮通过输出节点与轴间施加固定副,齿轮之间施加碰撞力接触,各轴与对应箱体轴孔输出节点施加转动副,输入轴端施加转速驱动,输出轴端施加负载转矩。 最后得到平行轴齿轮箱刚柔耦合模型,如图3所示。 图3 齿轮箱刚柔耦合模型 在ADAMS中,齿轮传动是通过齿轮的碰撞接触实现的,须采用impact函数进行齿轮碰撞接触定义。其中,等效刚度系数的取值参考赫兹(Hertz)接触理论[14-16]。仿真时间为1 s,仿真步长为5 000,积分器选择S12。 本文在仿真时转速采用低速900 r/min和高速2 400 r/min两种转速,分别对健康齿轮箱和带有0.4 mm齿根裂纹的齿轮箱进行仿真分析。其中,DDS齿轮箱故障实验台的平行轴齿轮箱如图3所示。 行星轴齿轮箱的减速比为i′=27:1,则仿真时两种输入轴转速设置为: (14) (15) 仿真电机驱动选择step函数形式,具体用step函数表示为: STEP(time,t1,0d*time,t2,nd*time)+STEP(time,t2,0d*time,t3,nd*time)+STEP(time,t3, 0d*time,t4,-nd*time) 上述step函数的意义为: t1时刻到t2时刻,转速值由0匀加速到n;t2到t3时刻保持电机转速不变t3到t4时刻,转速值由n匀速减为0。 笔者对模型施加驱动转速200 deg/s,设置仿真时间为1 s,仿真步长为5 000步。根据以上参数设置,通过仿真获得齿轮1、2的啮合力以及齿轮2的Y方向角加速度时域信号。 为了对比响应差异,笔者取仿真匀速段的6~7个响应周期为研究对象,得到仿真结果如图(4,5)所示。 图4 不同转速下健康和有0.4 mm齿根 裂纹的齿轮1、2的啮合力 图5 健康和有0.4 mm齿根裂纹的齿轮2在Y方向的角加速度 通过图(4,5)可以看出: (1)同一转速下齿根裂纹不会造成齿轮啮合力突变。有齿根裂纹时啮合力会出现周期性的高频“冲击”的现象,且随着转速的提高周期性的高频“冲击”现象更加明显; (2)同一转速下齿根裂纹会造成齿轮角加速度突变。有齿根裂纹时角加速度会出现周期性的高频“冲击”的现象,且随着转速的提高周期性的高频“冲击”现象更加明显。 将后处理结果中输出轴与箱体轴孔处连接节点34258的1 s内时变角加速度,通过FEA load以Excel数据表格导入到本文第2部分的MATLAB传动系统动力学模型程序中,运行程序得到齿轮箱输入轴Y方向加速度频谱,如图6所示。 图6 健康和带有0.4 mm齿根裂纹的齿轮传动系统在两种转速下的仿真频域图 由图6可以看出:健康状态下在齿轮啮合频率及其倍频附近处出现明显的幅值; 含齿根裂纹故障时,齿轮啮合频率及其倍频处的幅值明显增大,同时在啮合频率及其倍频两侧出现较为丰富的边频带,且边频幅值随转速的增大而增大。 该现象表明,齿轮出现裂纹故障时,在轮齿啮合过程会产生较大的振动冲击,且冲击对时域信号幅值进行了调制。 为验证上述仿真结果的准确性和可靠性,笔者在DDS齿轮故障模拟实验台上进行实验验证。 实验时数据采集频率设置为12 000 Hz,采样时间取实验启动稳定运行以后10 s。为了与仿真结果一致,实验采用线切割的方式在齿轮2的某个轮齿上沿轮齿中心线夹角60°的位置加工长度为0.4 mm的裂纹;分别在900 r/min和2 400 r/min转速下采集正常和带有齿根裂纹故障的齿轮箱振动信号。 齿轮故障模拟实验台及传感器置点如图7所示。 图7 齿轮故障模拟实验台及加速度传感器置点 通过计算得到不同转速下齿轮箱中各旋转轴转频及齿轮啮合频率,如表2所示。 表2 不同转速下各轴转频及齿轮啮合频率 健康状态和齿根裂纹故障时的测取得的齿轮箱振动信号频谱,如图8所示。 图8 健康和刻有0.4 mm齿根裂纹的齿轮箱在两种 转速下Y方向振动加速度实验频域信号图 从图8可以看出: 健康状态下在齿轮啮合频率的倍频处出现明显的幅值;含齿根裂纹故障时,齿轮啮合频率及其倍频处的幅值明显增大;同时,在啮合频率及其倍频两侧出现丰富的边频带,且边频幅值随转速的增大而增大,这与仿真结果一致。 本文通过MATLAB对平行轴齿轮箱传动系统建立了扭转振动模型,通过ANSYS、ADAMS对平行轴齿轮箱进行了刚柔耦合建模;综合考虑齿轮基体形变、齿轮啮合刚度计算时基圆和齿根圆的选取、齿轮及箱体柔性化处理3个方面,将刚柔耦合模型的输入端节点角加速度信号数据导入扭转振动模型中,通过计算得到了齿轮2在Y向加速度频谱;最后通过仿真与实验,证明两者结果一致。 笔者通过研究,得到如下结论: (1)同一转速下齿根裂纹不会造成齿轮啮合力突变。有齿根裂纹时啮合力会出现周期性的高频“跳跃”的现象,且随着转速的提高周期性的高频“跳跃”现象更加明显;同一转速下齿根裂纹会造成齿轮角加速度突变。有齿根裂纹时角加速度会出现周期性的高频“跳跃”的现象,且随着转速的提高周期性的高频“跳跃”现象更加明显; (2)健康状态下在齿轮啮合频率及其倍频附近处出现明显的幅值;含齿根裂纹故障时,齿轮啮合频率及其倍频处的幅值明显增大,同时在啮合频率及其倍频两侧出现较为丰富的边频带,且边频幅值随转速的增大而增大。该现象表明齿轮出现裂纹故障时,在轮齿啮合过程会产生较大的振动冲击,且冲击对时域信号幅值进行了调制。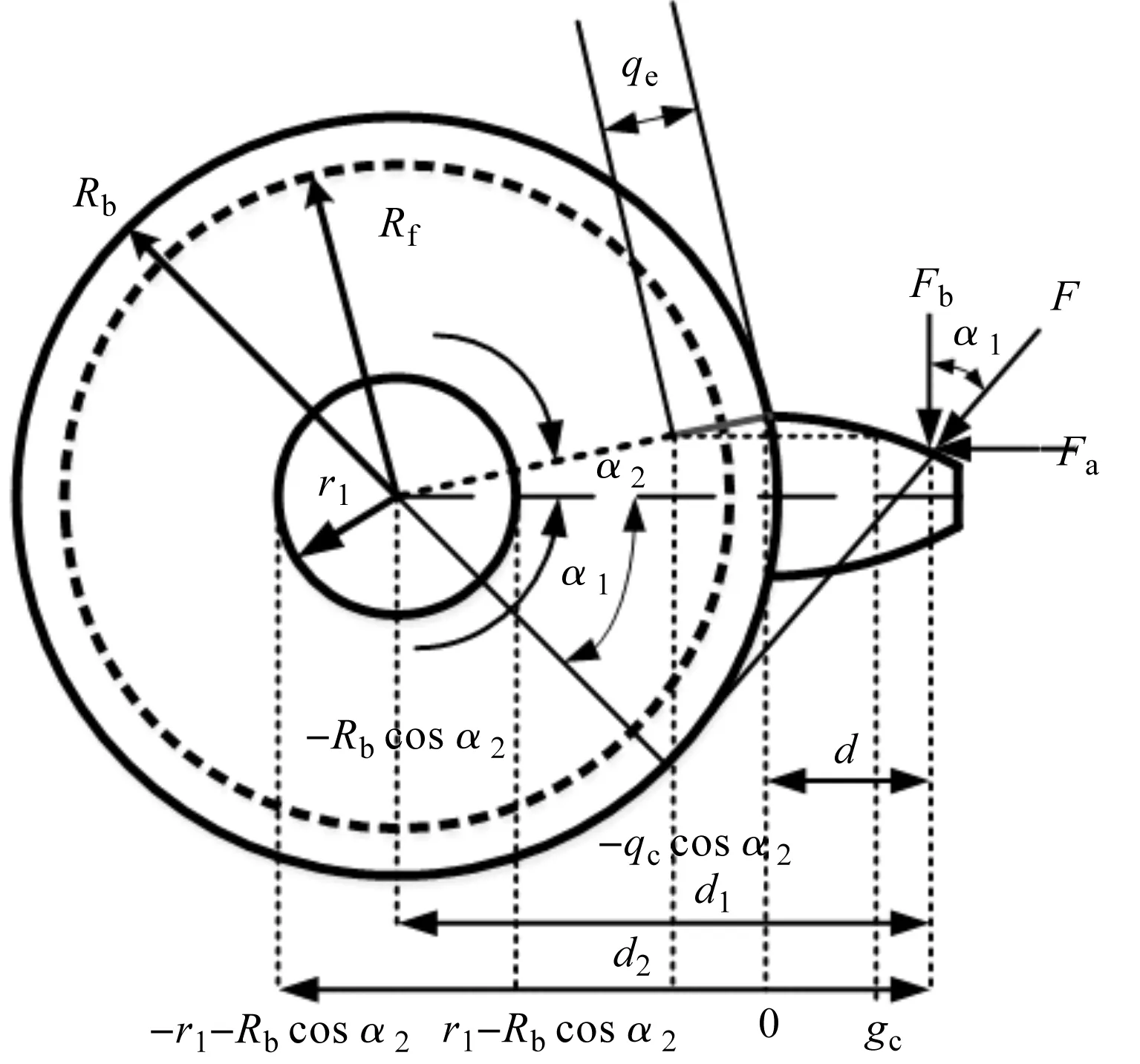
2 平行轴齿轮箱传动系统动力学模型
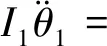
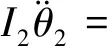
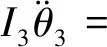

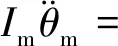
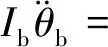
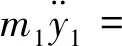
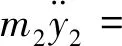
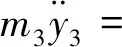
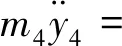
3 平行轴齿轮箱刚柔耦合动力学仿真

4 实验验证


5 结束语

