基于系统动力学的农产品两阶段定价仿真研究

陈见标，钟结枝 CHEN Jianbiao, ZHONG Jiezhi

（1. 广州工商学院，广东 广州510850；2. 广州科技职业技术大学，广东 广州510550）

0 引 言

中国是世界上最大的农产品消费国，合理的农产品价格对城市居民的生活质量意义重大，目前我国农产品市场的供求环境具有消费半径较小的特点[1]。零售商的零售价格是消费者购买农产品数量的重要影响因素之一，合理的定价有利于零售商获取最大的利润，同时维持一个良好、稳定的供需市场。

这些年来，关于农产品零售定价的研究逐渐得到学者们的关注。部分学者从零售商的角度出发，研究农产品定价的合理机制问题。李琳、范体军考虑了农产品实时价值损耗，分别对固定定价、动态定价以及带有降价时点三种不同的定价模式构建单周期零售商决策模型，通过分析最优策略与关键参数之间的关系，发现价值衰减系数越大，库存成本参数越大，三种模式下的总体零售价格越小，价格的下调幅度越大，而两个参数对降价折扣时间点的影响却截然相反[2]。结果还表明，灵活定价策略有助于零售商获取更大的市场需求量及更大的收益[3]。与上述学者不同，钱大胜从零售业态方面考虑，结合经济学、营销学等理论对集贸市场和超市的定价机制进行对比，发现两者在经营目的、税负、经营成本和品牌效应等方面都存在较大差异，研究结果显示，为了实现销量和利润的增长，超市应该在控制经营成本下下调农产品价格，而集贸市场需要充分利用新鲜、便利、灵活的优势，进一步提升农产品的品牌形象及个体工商户的诚信度[4]。

农产品的销售最终还是以提高城市居民的生活水平为目标。另一部分学者从消费者的角度出发对农产品的定价进行研究。王磊、但斌考虑了消费者偏好的多样性，构建了消费者时变选择模型，分析了零售商的最优定价和保鲜投入，研究了不同市场容量对零售商的利润增加值、最优定价及最优保鲜投入的影响方向[5]。王婧、金鑫、杜佳杉研究了顾客导向下网络销售模式的农产品定价影响因素，研究结果显示，价格是影响销量最敏感的因素，零售商应当给顾客让渡价值从而提高顾客满意度，以及密切注意顾客的消费能力、消费偏好以及消费行为[6]。唐跃武、范体军、刘莎考虑了消费者的策略性行为基础上，对零售商的单阶段和两阶段定价及库存决策模型进行构建，分析了农产品价值剩余率对消费者行为、零售商最优定价、最优库存水平以及零售商利润的影响机理，研究结果显示，单阶段模型与两阶段模型存在较大差异，前者是零售商最优价格和最优库存水平与农产品价值剩余率变化方向相同；后者在第二阶段最优价格随价值剩余率的变化趋势可能存在阈值[7]。

上述学者大多从数学建模的方法进行研究，只能分析最终的结果，不能显示出对过程的变化。农产品零售系统十分复杂，影响因素较多。系统动力学是一门结合系统论、控制论、信息论、模拟技术等发展起来的、擅长分析高阶、非线性时变、复杂系统的定性与定量分析相结合的工具，特别适合用于农产品零售过程的动态复杂系统。本文应用系统动力学理论对农产品零售过程进行建模研究。通过分析农产品零售系统的影响，构建农产品零售过程的两阶段定价系统因果关系图和流图，建立运算方程进行仿真研究，对相关参数进行敏感性分析。

1 农产品零售过程的系统动力学模型构建

1.1 农产品零售过程的系统动力学因果关系图构建

对农产品零售过程进行分析，以累计收益为研究目标，确定了农产品零售系统的边界，系统涉及的要素包括：零售商订货率、零售商库存、订货成本、库存成本、总成本、需求率、零售价格、销售收入、降价幅度、累计收益。各要素间的因果关系如图1 所示。

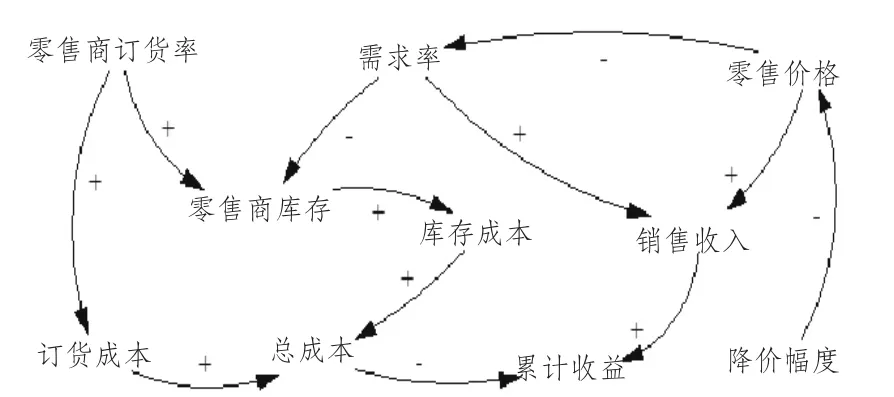
图1 农产品零售系统各要素的因果关系图

图1 中带箭头的线段表示两个要素之间的因果关系，若干要素连成的链条就是因果关系链。箭尾的要素影响箭头的要素，但箭头的要素不影响箭尾的要素。线段上的符号表示两者之间相互影响性质，带“+”的线段表示箭尾的要素对箭头的要素有正向作用，带“-”的线段表示箭尾的要素对箭头的要素有负向作用。

由图1 可知，零售商订货率对零售库存的订货成本均有正向作用；需求率对零售商库存有负向作用，对销售收入有正向作用；零售商库存对库存成本有正向作用；库存成本和订货成本对总成本都有正向作用；零售价格对需求率有负向作用，对销售收入有正向作用；降价幅度对零售价格有负向作用；销售收入对累计收益有正向作用；总成本对累计收益有负向作用。

1.2 农产品零售过程的系统动力学流图构建

根据农产品零售系统各要素的因果关系图，绘制出农产品零售系统动力学流图，具休如图2 所示：

图2 农产品零售系统动力学流图

由图2 可知，农产品零售系统动力学流图包括五个状态变量、六个速率变量、七个辅助变量和四个常量，具体如表1 所示：

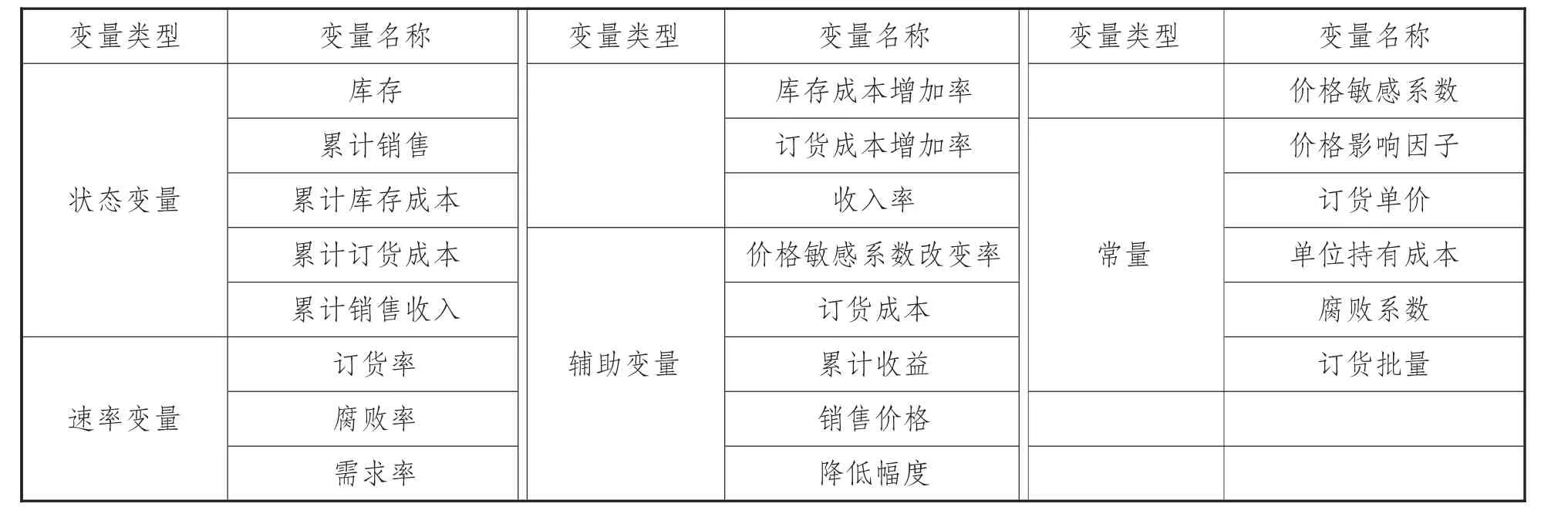
表1 农产品零售系统动力学流图变量表

1.3 农产品零售过程的系统动力学运算方程建立

利用Vensim 仿真软件提供的公式编辑器，建立农产品零售系统动力学模型的运算方程，具体如下：

库存=INTEG (订货率-需求率，初始值)

累计销售=INTEG (需求率，0)

累计库存成本=INTEG (库存成本增加率，0)

累计订货成本=INTEG (订货成本增加率，0)

累计销售收入=INTEG (收入率，0)

订货率=订货批量*PULSE TRAIN()

腐败率=库存*腐败系数

需求率=IF THEN ELSE (库存＞价格影响因子- (销售价格*价格敏感系数 )，价格影响因子- (销售价格*价格敏感系数)，库存)

库存成本增加率=库存*单位持有成本

订货成本增加率=单位时间订货成本

收入率=订货价格*需求率

价格敏感系数改变率=PULSE TRAIN()

订货成本=订货率*订货单价

累计收益=累计销售收入-累计订货成本-累计库存成本

销售价格=初始价格-初始价格*降价幅度*PULSE TRAIN()

降价幅度=1-STEP()

价格敏感系数=a+STEP (敏感系数改变率，t )

常量的赋值和辅助变量的部分赋值需要根据实际案例设定。

2 实例分析

2.1 实例仿真结果

本文对广州市某连锁超市的农产品零售现状进行调查，得到相关数据，具体如表2 所示：

表2 广州市某连锁超市的农产品零售数据

把表2 中的数据作为农产品零售系统动力学模型的参数代入模型进行仿真运算，得到结果如图3 所示。

由图3 可知，农产品零售系统的累计收益是齿轮状上升，这是由于定期订货而支付订货成本所导致的。累计收益在降价时点处的增长率提高，说明合理的降价空间会提升销售量，从而增加零售商的利润。

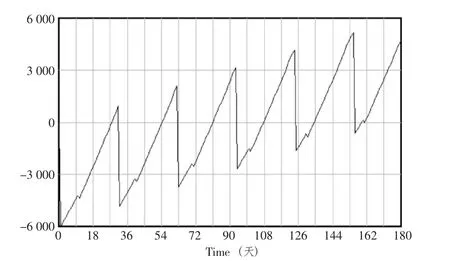
图3 实例仿真结果

2.2 敏感性分析

对订货批量和降价幅度进行敏感性分析，把订货批量设定为600 箱、900 箱和1200 箱进行仿真对比，得到到结果如图4 所示；把降价幅度设定为20%、30%和40%，得到结果如图5 所示。

由图4 可知，订货量为900 箱比订货量为600 箱和1200 箱所获得的利润更高，说明订货量不能太高，也不能太低，存在一个合理的订货量，使得零售系统获得最大化利润。

由图5 可知，降价幅度为30%比降价幅度为20%和40%时零售系统获得的利润更多，说明零售商需要一定程度的降价让利，但不能盲目降价，存在一个合理的降价幅度使得零售商获得最大利润。

3 结 论

本文基于系统动力学理论，对农产品零售系统进行仿真研究。分析了农产品零售系统的系统边界并确定各要素的相互影响关系；绘制了农产品零售系统动力学因果关系图；构建了农产品零售系统动力学流图并进行仿真运算方程的建立。通过广州市某连锁超市的数据进行实例分析，仿真结果显示：累计收益在降价时点处的增长率提高，说明合理的降价空间会提升销售量，从而增加零售商的利润。最后对订货批量和降价幅度进行敏感性分析，结果表明：订货量不能太高，也不能太低，存在一个合理的订货量，使得零售系统获得最大化利润；零售商需要一定程度的降价让利，但不能盲目降价，存在一个合理的降价幅度使得零售商获得最大利润。

图4 多种订货量仿真对比

图5 多种降价幅度仿真对比