基于均值回归价格过程重构隐含波动率

赵小银， 杨 柳

(兰州交通大学 数理学院，甘肃 兰州 730070)

金融衍生品定价理论是金融工程领域的重要组成部分，它促进了金融市场的发展。波动率是对原生资产回报率变化程度的度量指标。就某种程度而言，波动率是决定资产价格的重要因素，市场变化程度越剧烈，其波动率也就越高。通常，人们把由单个期权价格推导出的原生资产的波动率称为隐含波动率。许多研究表明隐含波动率是由资产价格与交割日期共同决定的函数。

衍生产品的定价始于对其原生资产价格过程的合理建模。假设在风险中性测度下，原生资产遵循均值回归过程(Schwartz模型[1])

dS=β(κ-lnS)Sdt+σSdW,

令C(S,t;K,T)表示原生资产S在t时的欧式看涨期权价格，W是标准布朗运动，参数σ被称为原生资产的局部波动率，K为敲定价格，T为到期日。对于上式，运用It-Doeblin公式，可以得到期权价格C(S,t;K,T)满足以下偏微分方程：

其中，r为无风险利率。利用基本解的已知性质，对局部波动率σ仅为S函数的情况，令G(S,t;K,T)=CKK(S,t;K,T)，将原问题转化为带终端观测值的标准反抛物问题：

这里，δ(S-K)为Diracδ函数。G(S,t;K,T)是上式的基本解，则G作为(K,T)的函数，它是上式共轭问题的基本解，即

接下来，令τ=T-t，则u(S,t;K,τ)=CK的函数满足

这里，H是Heviside函数。

作变换

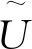
问题P1以下为二阶抛物型方程的初边值问题：

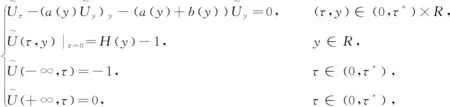
(1)

其中，|b|b1，|b|b2(b1和b2是两个已知的常数是期权价格，a(y)是(1)中的一个未知系数，即隐含波动率。附加条件为

在上述问题中，y∈R，因此该问题是一个无界区域问题，不利于数值计算。考虑到这一点，我们将问题转化为有界区域y∈[-L,L]的近似问题，其中L是一个较大的正数。又因为H(y)-1∈L1(-L,L)，所以其一阶导数是一个Diracδ函数，在之后的证明中较难处理。而C∞(-L,L)在L1(-L,L)中是稠密的，因此，选择ψ(y)∈C∞(-L,L)，使‖ψ(y)-(H(y)-1)‖L1<ε，ε>0是一个充分小的正数。继而又将问题进一步转化，其可以表示成以下形式：

问题P考虑二阶抛物型方程的初边值问题：

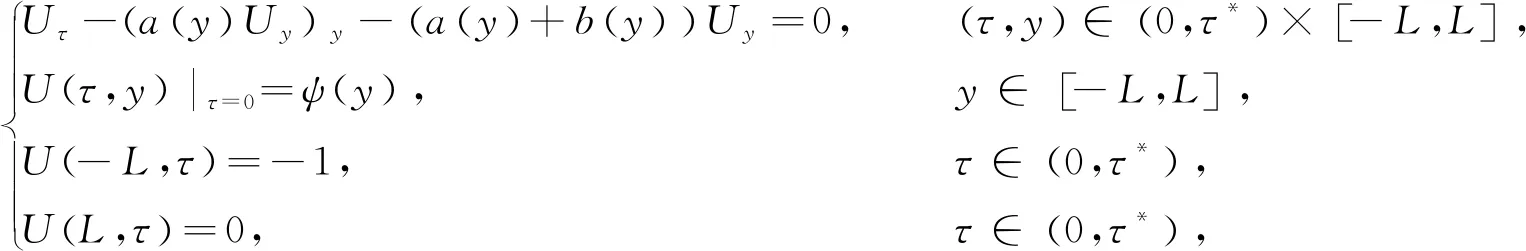
(2)

其中，U是期权价格，a(y)是(2)中的一个未知系数，即隐含波动率。附加条件为

U(τ*,y)=U*(y),y∈[-L,L]。

如何根据以上内容确定函数U和a(y)使其满足(2)？

在工业、物理、金融和一些其它应用领域中，抛物型方程的反问题得到了广泛关注。金融衍生物是一种风险管理的工具，它的价值依赖于原生资产的价格变化。1964年，P.Samuelson提出了与时间相关的原生资产的随机微分方程：

dSt=μ(t,St)Stdt+σ(t,St)StdWt,

其中，Wt是布朗运动，参数μ(t,S)和σ(t,S)被称为漂移率和原生资产的局部波动率。

Fischer Black和Myron Scholes[2]首先发现了如何构造衍生证券和原生资产的动态投资组合∏t。通过Ito引理，衍生证券u(t,S)的随机行为满足以下随机微分方程：

在没有套利机会的情况下，该投资组合的即时收益必须等于利率，即风险较低的资产(如银行存款)收益。因此，此等式采用以下偏微分方程的形式：

其中，无风险利率r和红利率δ是已知的常数。

正问题与反问题有着根本的区别。在一般情况下，逆问题在Hadamard意义下都是不适定的，而正问题则是适定的。如果一个物理问题的数学模型被称为适定的，则它具有以下三个性质：问题的解存在；问题的解只有一个；解持续依赖于数据即稳定性(见参考文献[3，4，5])。关于求解不适定问题，可以从最优控制理论的角度出发进行处理。Lions和Magenes[6]对描述分布参数系统的偏微分方程(椭圆型、抛物型和双曲型)的定解理论作了深入研究，通过引入变分不等式等工具，探讨了各类典型二阶性能指标的最优控制问题。杨晓清[7]研究了Fitzhugh-Nagumo方程的最优非线性边界和分布控制问题：

首先利用Schauder不动点定理证明上述控制系统的状态方程初边值问题的适定性，然后运用变分思想证明最优解的存在性，最后利用映射的可微性证明得到必要最优条件。

在文献[8]和[9]中，利用最优控制原理，从当前期权市场中，确定了方程

uτ-a(y)(uyy-uy)+(r-q)uy=0,y∈R,τ∈(0,τ*)

的波动率a(y)，并得到了一个稳定算法。

在文献[10]中，基于最优控制原理，研究了与黄金价格相关联的金融产品隐含波动率的反问题

并给出了一些数值实验。数值结果表明，算法是稳定有效的。

在文献[11]中，基于Black-Scholes模型推导出了一个新的模型

V(τ*,y)=V*(y),y∈ω⊆R,

该模型是一种套利模型，应用微局部分析法，证明了在金融市场上其解f(y)的唯一性。最后，重构了漂移率，提出并测试了该模型的数值算法。

本文利用最优控制框架(参见[12])讨论问题P。在第1节和第2节中，我们将问题P转化为最优控制问题P2，并证明了控制泛函极小元的存在性。在此期间，为了理论证明简单化，我们将非齐次问题P转化为齐次问题。在第3节中，我们得到了极小元必须满足的必要条件。在最后一节中，我们证明了极小元是局部唯一的。

1 最优控制问题

考虑以下最优控制问题P2：

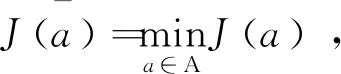
(3)

这里，

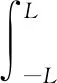
(4)

对于给定的a∈A，U(y,τ)是问题(2)的解，N是正则化参数。考虑隐含波动率的“微笑”或“偏斜”效应(见参考文献[13-14])，假设0<α0a(y)α1(α0和α1是两个已知的常数)是合理的。

对于给定的a∈A，我们从Sobolev嵌入定理知道，a∈C1/2(-L,L)和‖a‖C1/2(-L,L)C(这里C为一个常数)。抛物型方程的已知理论(见[15])保证了初边值问题(2)的唯一解U(y,τ)∈Cα,α/2((-L,L)×[0,τ*])∩C2+α,1+α/2(((-L,L){0}×[0,τ*])。

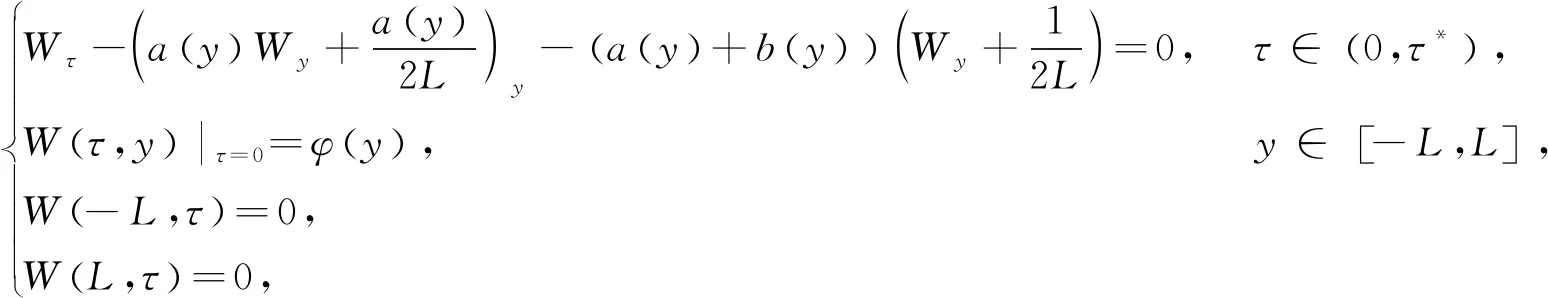
(5)

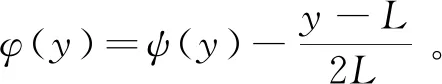
引理1.1如果W(y,τ)是初边值问题(5)的解。那么

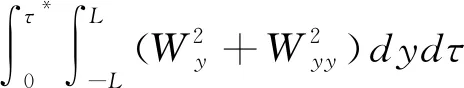
(6)

该引理的证明是标准的。

引理1.2如果U(y,τ)是初边值问题(2)的解，那么

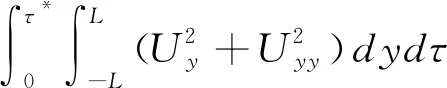
(7)

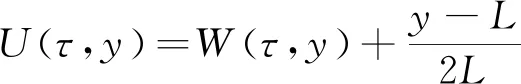
2 存在性

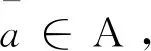
证明设(Un,an)是极小化序列。因为J(an)C，推断

‖an‖L2(-L,L)C(常数C与n无关)。

利用soblev嵌入定理，我们得到了‖an‖C1/2(-L,L)C。

所以，

‖Un(y,τ)‖C2+1/2,1+1/4(ω)C, ∀ω⊂⊂Q,

其中，Q=(-L,L)×[0,τ*]。

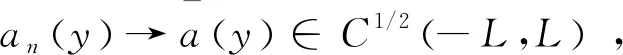
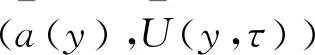
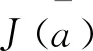
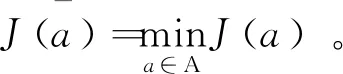
3 必要条件

定理3.1设a为最优控制问题(3)的解。则存在满足以下系统的三元组(U,V;a)

(8)

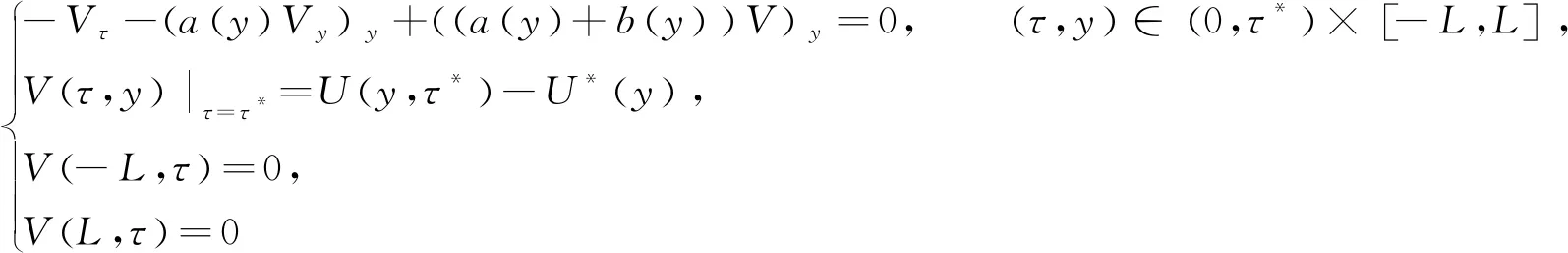
(9)

和

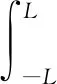
(10)

对任意h∈A都成立。

证明对于任给h∈A，0δ1，有aδ≡(1-δ)a+δh∈A。

设Uδ是初边值问题(2)当a=aδ的解。因为a是最优解，因此根据(4)式可以得到

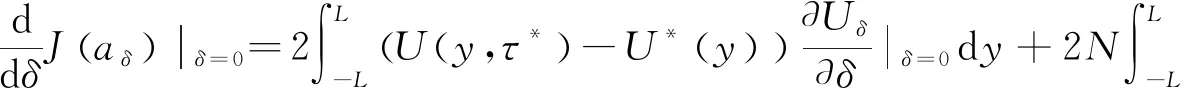
(11)

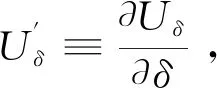
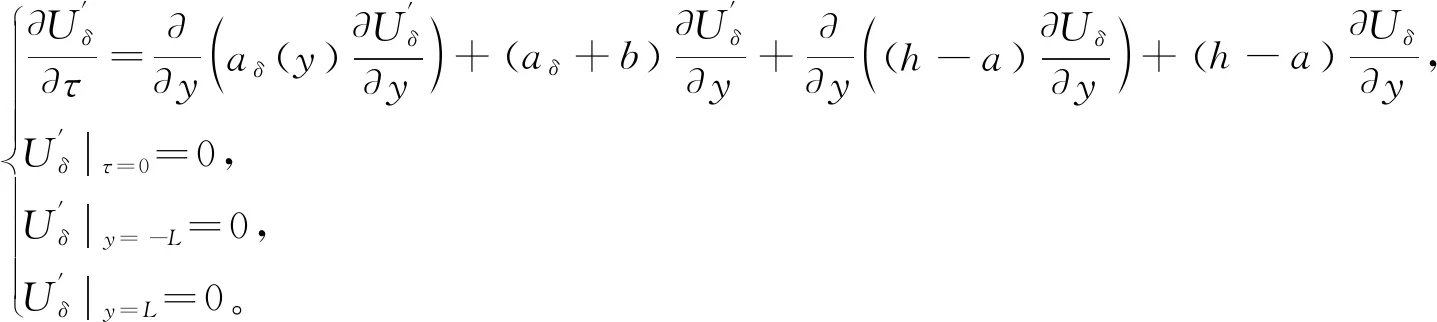
(12)

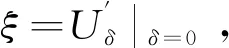
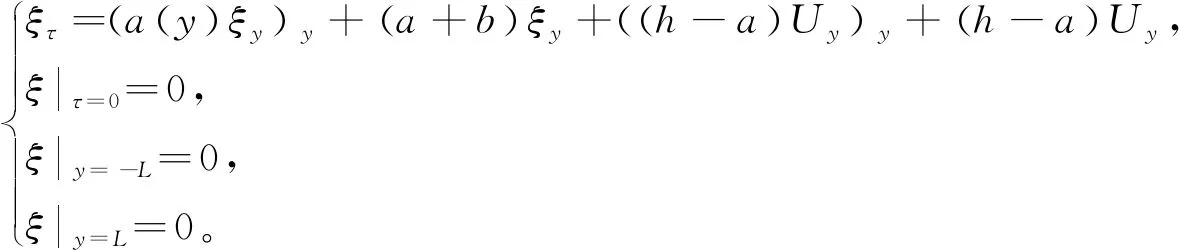
(13)

从(11)式中，我们可以推得

。

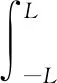
(14)

假设V是下列方程组的解：

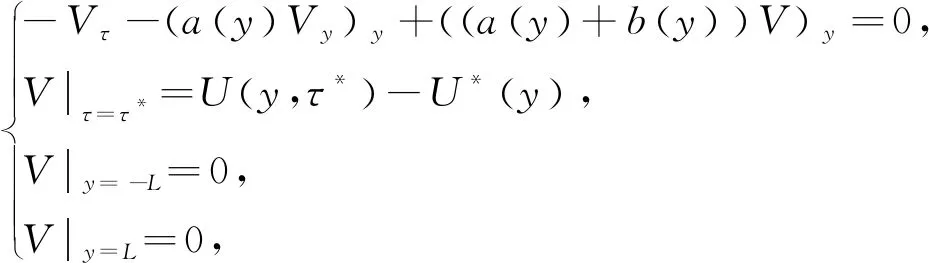
(15)

由(13)式和(15)式，得

(16)

又由于

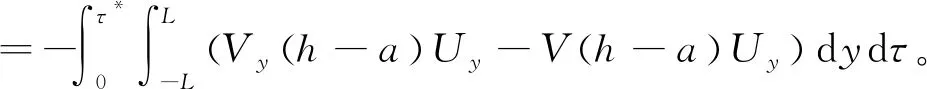
(17)

结合(14)式、(16)式和(17)式，可以容易地获得

。

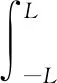
(18)

定理3.1证明完毕。

4 唯一性结果

引理4.1对于任何有界连续函数f(y)∈C[-L,L]，我们有

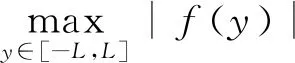
其中y0是一个固定点。

证明|f(y)|

引理4.1证明完毕。

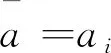
a1-a2=A,U1-U2=U,V1-V2=V,

那么U和V满足

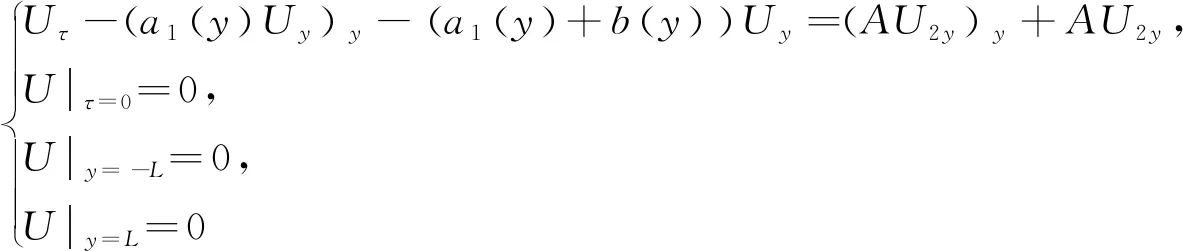
(19)

和

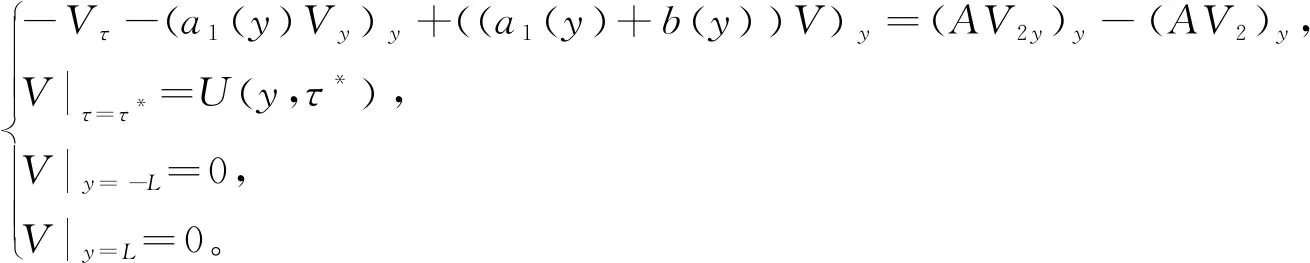
(20)

引理4.2如果Vi(y,τ),(i=1,2)是初边值问题(9)的解，那么

,

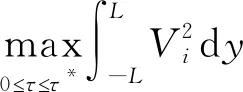
(21)

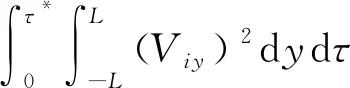
(22)

和

。

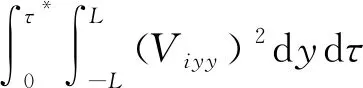
(23)

该引理的证明是标准的。

引理4.3对于方程(19)，有估计

,

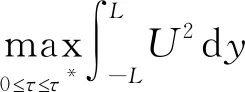
(24)

,

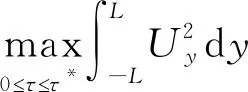
(25)

这里C是一个常数。

证明(24)式的证明是标准的。根据方程式(19)，对于0<ττ*，我们有

接下来，我们得到以下不等式：

利用Gronwall不等式，可知

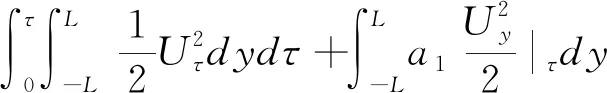
引理4.3证明完毕。

引理4.4对于方程(20)，有估计

,

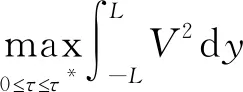
(26)

和

,

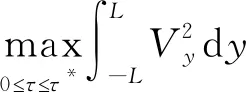
(27)

其中C是一个常数。

证明(26)式的证明是标准的，(27)式的证明与引理4.3的证明类似。

定理4.5假设a1(y)，a2(y)是最优控制问题P2的两个极小元。如果存在点y0使得

a1(y0)=a2(y0),

则当τ*≪1时，可以得到

a1(y)≡a2(y),对于任意的y∈[-L,L]。

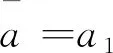
(28)

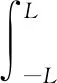
(29)

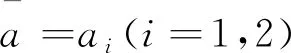
从(28)式和(29)式中得

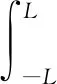
(30)

根据引理4.3，引理4.4和(30)式得到

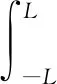
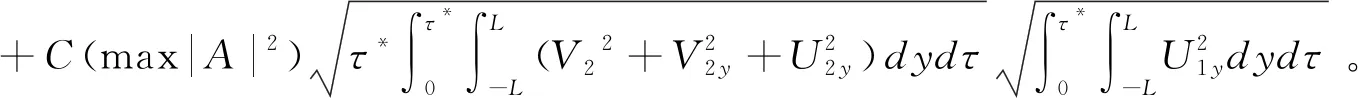
(31)

由于引理1.2，我们有

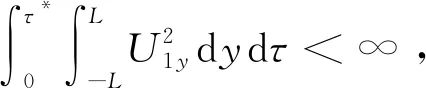
(32)

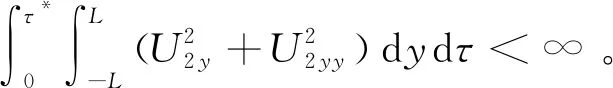
(33)

由于引理4.2，我们有

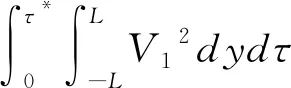
(34)

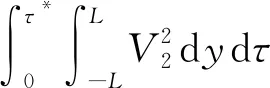
(35)

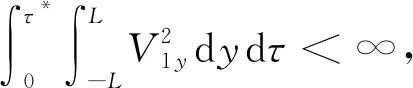
(36)

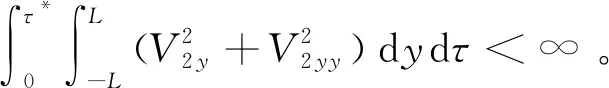
(37)

从定理4.5的假设出发，存在一点y0∈[-L,L]使得

A(y0)=a1(y0)-a2(y0)=0

。

(38)

通过引理4.1，可知

。

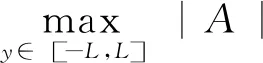
(39)

从(30)式到(39)式，得到以下结论

。

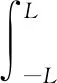
(40)

当τ*≪1，使得

C2τ*

(41)

那么，我们可以得到

。

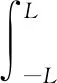
(42)

因此，

A=0

。

(43)

从假设A(y0)=0出发，可以得到

A(y)=a1(y)-a2(y)≡0

。

(44)

定理4.5证明完毕。

本文主要关注了基于均值回归价格过程重构隐含波动率的反问题。运用偏微分方程的最优控制理论，讨论了隐含波动率系数的存在性，并且证明了最优解的局部唯一性。这些结果为数值仿真提供了强有力的理论基础。在接下来的工作中，我们将利用金融市场上的一些具体观测数据，结合计算机编程得到隐含波动率的数值解。这些结果可以用来预测未来金融衍生品的价格走势，还可以为相关金融行业的从业者做出恰当的投资策略提供一些参考。