浅谈思维导图在高中数学审题中的应用

卢晓涵

【摘 要】思维导图作为一种表达发散性思维的有效图形思维工具，被很多研究人员和一线教师用于科学研究和实践教学中。它作为一种可视化的思维工具，在高中数学审题过程中发挥了其独特的作用，它使学生有了更严密的审题过程和解题思路，同时，也让学生正确的找到已知条件和隐藏条件，即达到解题的目的又培养了学生的创新思维、探究思维、发散思维等能力。

【关键词】思维导图;高中数学;审题

在高中数学的解题过程中，很多学生为了加快解题速度，只注重做各种试题很少注重回归知识理解基础上的问题理解结构梳理分析，也就是说并沒有对题目进行详细的审阅。这就造成学生在做题过程中出现错解和漏接现象。面对这样的问题，很多研究人员和一线数学教师也不断地对自己的教学方法和教学研究内容做出调整，以及时的帮助学生在解决数学问题时，能全方位、多层次的考虑问题;能使所学的知识进行正确迁移应用，独立深思并挖掘出问题的本质，已达到顺利正确解题的效果。

思维导图的出现无疑给研究人员和数学学习者带来一道独特的亮光，笔者结合自己的实践经验，浅谈一下思维导图在高中数学审题中的应用，从根本上找到正确的审题方法。

一、思维导图的定义和用途

思维导图是由英国的心理学家、教育学家托尼·博赞（Tony Buzan）提出研发的。是一种直观可视的发散思维工具。

通常由一个中心概念或主题向外发散出成一系列的关节点，每一个关节点代表与中心主题的一个连结，而每一个连结又可以成为另一个中心主题，再向外发散出成众多的关节点，呈现出放射性立体结构，就如同大脑中的神经元一样互相连接，形成您的个人数据库。

思维导图充分运用左右脑的机能，利用记忆、阅读、思维的规律，协助人们在科学与艺术、逻辑与想象之间平衡发展，从而开启人类大脑的无限潜能。思维导图因此具有人类思维的强大功能。

二、思维导图在数学审题中的应用

（一）利用思维导图整合出知识框架是审题的前提条件

高中数学教材模块多知识点琐碎，很多学生来说，学过的知识过段时间遗忘或发生混淆记错，知识散乱无联系，缺少对知识的来龙去脉的认识。因此，大脑中没有知识体系，构建不出知识结构，在处理数学题目时也很困难。另外，就教师而言，按照传统的教学模式，只是用数学语言和数学符号传授知识，相当抽象，而且学生不易接受。因此，复杂、混乱、抽象不易记忆的数学知识对不同层次的学生造成了不同的学习障碍，而教师在教学过程中也感到极其吃力。因此，教师在教学过程中利用思维导图引导学生理清知识之间的逻辑关系、使学生自主构建有机的知识体系，培养学生的审题能力和运用知识的能力，使各个层次的学生都能利用思维导图来提升自己的思维能力和自我反思能力。

比如，学习导数这一部分知识时，教师要适当放慢脚步引领学生进行审题，首先借助于思维导图让学生理解导数的概念，然后让学生充分理解函数的和差积商的导数以及符合函数的求导法则，最后让学生明白利用导数可以做什么，利用数形结合思想让学生明白函数单调递增、单调递减以及极值最值等概念。

因此，教师可以设定一下导数知识的思维导图，展开自上而下的学习探究。

（二）利用思维导图展开解题思路提高审题的严谨度

在数学学习过程中，很多学生尽管掌握了很多知识、方法、技巧，但是自己独立面对问题时想不起用，但一经提示就会了;而有的面对陌生的或者没做过的题目时往往没有解题思路;更有一部分学生是在解题时，一般能建立起大致思路，但在具体操作中就进行不下去或者出现错误。这些学生大都是以“模仿+记忆”为主，缺少解题思维活动的经验和策略，缺少必要的数学技能。

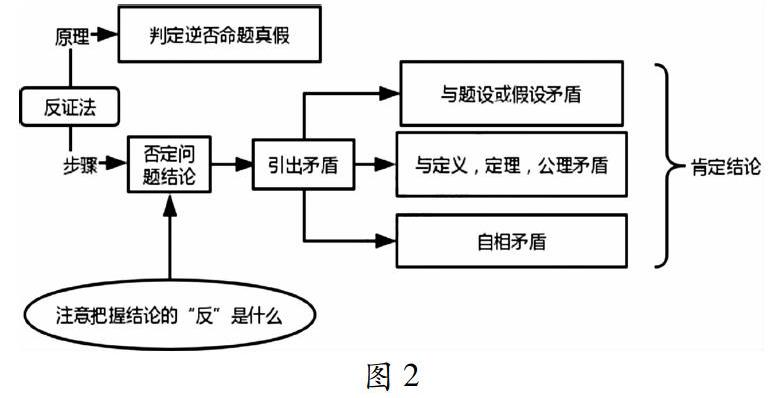
例1：已知a+b+c>0，ab+bc+ca>0，abc>0.求证a>0，b>0，c>0.证明题方法有两种，直接证明和间接证明。如果利用直接证明思路并不明显，所以采用间接证明的反证法证明，这就要求对“反证法”解题步骤和使用条件回顾一遍，思维导图如下图：

通过以上审题过程，就有了如下证明——反证法：假设a，b，c不全是正数，即至少有一个小于或者等于0.又abc>0，则设a<0，则bc<0.∵b+c<-a>0，∴-a（b+c）>0，∴a（b+c）<0，又bc<0，∴bc+a（b+c）<0.即ab+bc+ca<0，与ab+bc+ca>0矛盾，所以假设不成立，故a>0，b>0，c>0.

因此，在做题过程中，面对这种情况，学生可以采用思维导图将知识、方法体系化，借助直观的图形进行形象的记忆，可以加强对数学概念、公理、定理以及数学思想方法等的理解记忆。通过思维导图审题分析检索所学解题方法技巧，逐渐打开思路，促使思路更严谨、清晰。

（三）利用思维导图充分找已知挖隐藏条件

每一道题的切入点都是已知条件，已知条件是解题的基础，充分审视题目中的已知条件及潜在条件，是顺利解题的重要保障。在审题时，教师一方面要引导学生认真分析每一句话，积极思考，反复审读题，挖出题目中的核心词语，关键条件，并展开探索性的联想——由每个条件可以转化出哪些新的条件;另外有些题目的条件比较隐含，隐含条件只要挖掘出来，就为解题提供新的条件和依据，解题思路便会浮上水面。

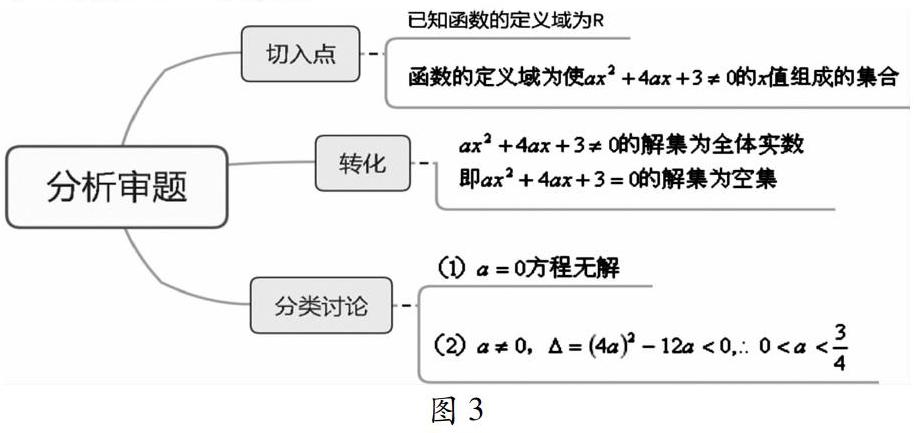
本题的切入点是已知函数的定义域为R，由于出现分式，进一步挖掘隐含条件方程的解集是空集。另一个隐含陷阱是方程式一次方程还是二次方程，每种情况都对应一个参数a的取值范围。审题过程非常严谨，思路明了。最后的取值范围是0，34。因此，在审题时利用思维导图让看不见的思维形象化，使整个解题思路更清晰明了。所以，思维导图在审题过程中发挥着重要的作用。

总之，在整个的数学学习过程中，思维导图作为一种可视化的工具，可以整合知识构建知识框架，让模糊不清的数学概念公式定理定义更清晰，加强学生的创新思维、探究思维、发散思维，增强学生的知识运用能力。使学生在审题时，有了更严谨的思维模式和正确的解题思路，提高了学生数学解题过程中审题分析能力和解决问题的能力。同时，也提高了教师的数学课堂效率和教学理论素养，提高其专业化素质和专业化水平，实现数学教师的专业发展。

参考文献：

[1]白雪松.浅谈高中数学解题过程中的审题策略[J].数理化解题研，2015（12）.

[2]於巧云.思维导图在高三数学复习中的应用[J].数学学习与研究，2011（7）.

[3]严加明.如何在高中数学习题课中培养学生审题能力[J].数理化解题研究，2013（5）.