电力机车永磁同步电机自适应模糊终端滑模控制

谢程程,王桂荣

(1.西安铁路职业技术学院,陕西 西安 710026;2.中国计量大学机电工程学院,浙江 杭州 310018)

电力机车运行经过道岔及轨缝处易受突变载荷冲击并以时变负载转矩的形式通过轮对、轴箱和联轴节传至机车永磁同步电动机(PMSM,permanent magnetic synchronous motor)转轴,影响电机的转速控制精度[1-2]。因此,在提升局部结构强度,增强连接件稳定性的同时应通过合理设计超扭转转矩观测器(STO,super twisting observer)削弱时变转矩对电机运行的不利影响。

研究旨在设计机车PMSM转速控制器及针对踏面复合时变转矩的超扭转观测器。采用自适应模糊逻辑系统逼近观测器误差导数以改善滑模面抖振;结合类势能函数的相关性质,构造复合非奇异终端滑模面设计自适应模糊终端滑模控制器,使得系统快速精确跟踪参考转速,抑制轴电流及滑模面抖振,兼顾动态响应快速性和时变负载鲁棒性。

1 自适应模糊终端滑模控制器设计

机车PMSM在d-q坐标系下的数学模型[3-4]为

(1)

其中:ud、uq、id、iq分别为定子电压及电流d轴和q轴分量;ω为转子角速度;R、L分别为定子电阻及电感;ψf为磁链;p0为极对数;J为转动惯量;B为粘滞阻尼;TL为转矩。

1.1 超扭转转矩观测器设计

(2)

(3)

设计STO输出至控制器部分的控制量为

(4)

1.2 基于类势能的自适应模糊终端滑模控制器设计

构建类势能函数如下:

(5)

其中:0<α<1,β>0。

对其求导得

再次求导得

引理1函数P(x)和p(x)满足如下性质[6]:

(1) 若x=0,P(x)=p(x)=0;若x≠0,P(x)>0。

(2)P(x)连续可微,p(x)单调递增且p(x)≤βα。

假设参考转速ω*各阶导数存在,定义跟踪误差为

e(i)=ω*(i)-ω(i),i=0,1,2

(6)

根据引理1中类势能函数性质构造复合非奇异终端滑模面为

(7)

对式(7)求导得

注意控制器内部关系:

(8)

将式(8)代入滑模面导函数,并整理得

(9)

针对式(9)中观测器误差导数即未知变量Δ,根据模糊逼近理论[7-8],采用径向基神经网络对其估计。

定义

Δ=φ*Tξ(S)+ζ,

(10)

设计未知变量Δ的估计值为

(11)

则Δ的估计误差满足:

与滑模面S相乘后得

设计自适应模糊终端滑模控制器为

(12)

(13)

(14)

2 仿真结果及分析

构建SIMULINK仿真环境对机车PMSM转速控制系统采用自适应模糊终端滑模控制器(AFTSMC,adaptive fuzzy terminal sliding mode control)进行仿真研究。设定参考转速(rad/s)的复合信号为

考虑轮对静载荷为定常负载转矩,踏面冲击载荷为时变负载转矩,二者合成后的转矩(kN·m)为

TL=30+20sin (2·t)。

机车PMSM转速控制系统参数见表1。

图1、图2分别为角速度参考跟踪及负载转矩估计跟踪曲线,跟踪误差以对数形式呈现于图3。分析图1中子图1可知,采用AFTSMC的PMSM转速控制系统,其实际转速输出能够迅速(约0.2 s)跟踪参考转速;参考图3中子图1、子图2,可知转速误差维持在10-1～100内,误差对数数量级稳定说明系统输出跟随性能较为理想。分析图1中子图2、子图3可知,在取样窗口内,波谷处误差维持在0.7 rad/s;波峰处误差维持在0.7 rad/s,说明参考转速与实际转速之间的误差稳定在0.7 rad/s,与相应误差对数值曲线表征一致。图2中分别考察波谷及波峰采样窗口(见图2中子图1及子图2),可知STO估计输出可对负载转矩实现较为准确的估计,参照图3可知,估计误差数量级稳定在波峰10-1至波谷10-13范围内,说明STO估计输出稳定且精确。图3中对滑模面求取对数,子图2中滑模面在±0.1范围内波动,经0.3 s(0.15～0.45 s)小幅颤振后收敛于0的小邻域范围内;图3中子图1表明滑模面收敛于0,光滑且无剧烈抖振。

表1 机车PMSM参数标称值

图1 角速度参考量跟踪曲线Fig.1 Angular speed reference tracking curve

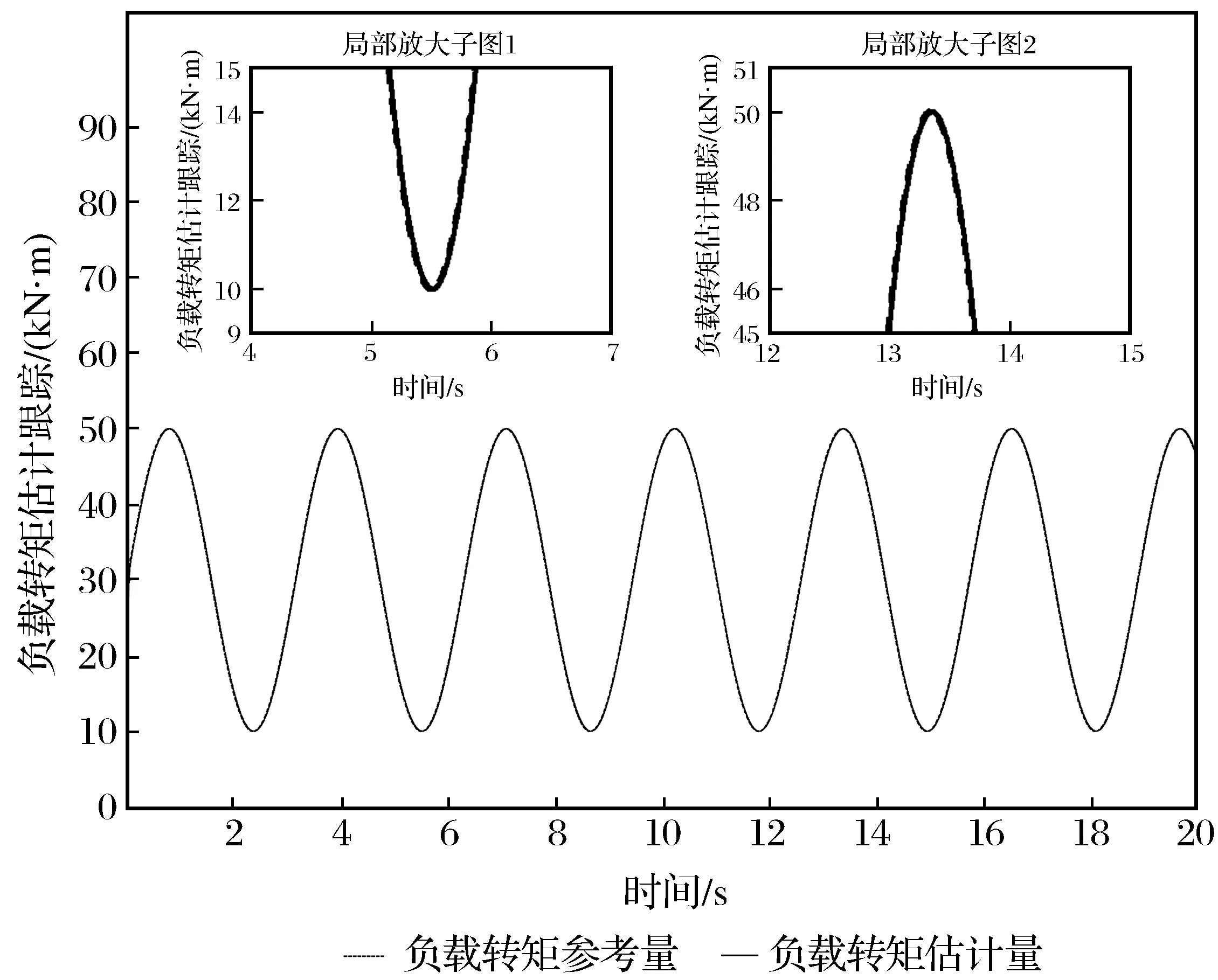
图2 负载转矩估计跟踪曲线Fig.2 Load torque estimation tracking curve

图3 负载转矩、输入转速跟踪及滑模面误差对数曲线Fig.3 Load torque,input speed tracking and sliding mode surface error logarithm curve

3 结论

研究针对机车PMSM转速控制系统中存在的时变负载扰动,结合类势能函数的相关性质,构造了复合非奇异终端滑模趋近律,设计了基于STO的自适应模糊终端滑模控制器,其具有如下优点:

(1) 通过对非奇异终端滑模幂次因子的设计,避免了普通终端滑模控制器设计中存在的奇异问题。

(2) 在非奇异终端滑模面中引入类势能函数,并根据误差面导数的阈值选取不同的滑模趋近律形式,使得系统在有限时间内快速收敛。

(3) STO不受被观测信号缓慢变化的限制,可用于观测时变负载的变化情况,对其观测误差的导数采用模糊逼近,可实现对负载转矩的有效跟踪。