模糊需求下绿色同时取送货问题与算法研究

马艳芳，应 斌，康 凯，栾新凤

河北工业大学 经济管理学院，天津 300401

1 引言

目前，全球气候变暖问题日益突出，温室气体排放问题受到广泛关注。在1992 年制定的《联合国气候变化框架公约》中建立了应对未来数十年气候变化的长效机制。于2005年正式生效的《京都议定书》使得减少温室气体的排放量成为了发达国家的法律义务。同时，我国政府承诺到2020 年，我国二氧化碳排放量同比2005年减少50%～60%。十八届五中全会提出了“创新、协调、绿色、开放、共享”的发展理念，其中绿色是永续发展的必要条件。而交通运输业是温室气体的主要来源之一，其中物流运输占交通运输业碳排放量的比重最大，面临着巨大的减排压力。因此，减少物流运输作业中的碳排放量，实现绿色物流具有极强的现实意义。

近几年，车辆调度问题的低碳化研究已经引起了学者们的广泛关注。Sbihi 等[1]认为对传统车辆调度问题的研究目标不应局限于经济效益，还应考虑环境和社会因素，以有效减少碳排放。Palmer[2]研究速度与二氧化碳排放的关系，建立运输车辆的集成路径调度和碳排放模型。Demir等[3]认为运输车辆的油耗量与车速、加速度和载重等多个参数有关，进而影响碳排放量。Bektas等[4]综合研究多目标车辆调度问题，包括负载、油耗、温室气体、旅行时间、距离、成本，并权衡了各目标之间的关系，提出车辆调度问题有很大的减排空间。张春苗[5]建立低碳-定位车辆调度模型，并证明该模型能有效减少运输中的碳排放，但会使总成本增加。李顺勇等[6]基于多通路时变网络研究低碳车辆调度优化。史春阳[7]研究公路运输中油耗与CO2排放量的计算体系，并在此基础上重点研究同时取送货车辆调度问题（Vehicle Routing Problem with Simultaneous Pickup and Delivery，VRPSPD）中CO2减排因素对调度规划的影响。李进等[8]研究低碳环境下的车辆调度问题，提出使用中低的车辆速度有利于减少碳排放量。唐金环等[9]在时变网络下对含旅行时间和碳排放的多目标车辆调度优化问题进行研究。赵燕伟等[10]对多车型VRPSPD 问题进行了低碳路径研究。葛显龙等[11]研究开放式污染路径问题，提出碳排放计算方法，并建立了优化模型。以上文献研究了低碳条件下的车辆调度问题，促进了绿色物流的发展。然而，目前对绿色物流的研究往往只考虑了传统车辆调度问题下的碳排放问题，缺乏对顾客需求不确定性和同时取送货情况的考虑。

车辆调度问题是典型的NP 难题，通常采用启发式算法求解。符卓等[12]针对需求可离散拆分的车辆调度问题，提出具有特殊操作的禁忌搜索算法，增强算法搜索性能。谢九勇等[13]设计自适应禁忌搜索算法以求解带多软时间窗的车辆调度问题。潘雯雯[14]基于路径优化和路径改进，提出两阶段算法。张涛等[15]对蚁群算法进行改进，引入最大最小蚂蚁系统和基于排序的蚂蚁系统，并改进启发因子和初始化，以研究带车辆行程约束的VRPSPD。陈希琼等[16]针对多目标VRPSPD 问题，构造嵌入禁忌表的多目标蚁群算法求解。郭海湘等[17]基于单车场多车型提出三种混合算法，通过比较发现混合蚁群算法性能更优。葛显龙等[11]设计并改进自适应遗传算法，以求解开放式污染车辆调度问题。李进等[8]对低碳环境下的车辆调度问题，设计基于路径划分的禁忌搜索算法，采用三种邻域搜索方法。然而，单一算法一般都具有一定的局限性，如遗传算法易陷入早熟早收敛，禁忌算法对初始解依赖性较强，模拟退火算法对初始参数设置较敏感，蚁群算法收敛效率较低。近年来，学者对混合算法的研究逐渐深入，以克服单一算法的局限性。李陶深等[18]提出遗传算法与禁忌搜索算法的混合策略，并应用于VRPTW（Vehicle Routing Problem with Time Windows）问题。余丽等[19]将遗传算法与禁忌搜索算法相结合，以优化旅行商路径问题。混合算法策略相对于单一算法具有明显的优势，取得了不错的效果。

笔者梳理相关文献，选取近五年相关文献，选择与车辆调度主题完全契合文献，剔除同一作者相近题目，表1总结了车辆调度问题中与不确定环境、同时取送货和低碳相关研究。从表1 中可以发现有较多关于低碳与同时取送货的单一研究，关于模糊需求的研究较少，仅极少的文献研究了低碳取送货问题或模糊环境下的同时取送货问题。同时取送货车辆调度问题在传统的VRP（Vehicle Routing Problem）中考虑了顾客的取货需求，同时安排了送货与取货，从而降低了车辆的空载行驶里程，以追求成本最小。模糊需求车辆调度问题（Vehicle Routing Problem with Fuzzy Demand，VRPFD）考虑了客户需求的模糊性，把客户的需求量设置为三角模糊数，使该问题更符合实际情况。考虑碳排放的车辆调度问题（Low-Carbon Routing Problem，LCRP）在传统的VRP中考虑了社会经济效益，从经济车速、交通条件、道路条件、天气状况等因素考虑，降低配送过程中油耗和碳排放，实现低碳运输。本文在同时取送货问题研究中，考虑了低碳运输和顾客模糊需求，提出了以碳排放、油耗、服务总成本最低为目标的同时取送货车辆调度问题。随后，提出改进的混合算法策略，即遗传禁忌搜索算法（Genetic Algorithm with Tabu Search，GA-TS）求解该问题，以避免单一算法局限性。算法中，将惩罚因子引入适应度函数，处理违反约束的染色体；采用结合精英策略的选择算子，加速向最优解收敛；提出结合禁忌搜索算法的变异算子，提高算法的局部搜索能力。

表1 相关文献简明综述

2 问题描述及模型构建

模糊需求下绿色同时取送货车辆调度问题描述如下：配送中心使用单一类型的车辆给客户服务，同时满足顾客的取送货需求，且客户需求具有一定的模糊性。每辆车必须从配送中心出发，完成任务后返回配送中心不再服务，且每个客户只能访问一次。目标函数不仅考虑了与时间相关的服务成本，还考虑了油耗、碳排放成本，以此进行合理的路径规划，使总成本最小。另外，为了便于建模和求解，进行以下条件限制：只有一个配送中心；客户的具体信息已知，包括客户位置、服务时间等；车辆最大装载量能同时满足任意客户的两种需求；货车总数量能满足所有顾客的总需求；每个顾客有且仅有一次被服务。

2.1 期望模糊需求

现实生活中，客户往往很难给出一个十分精确的需求量及取货量。相反，客户往往会依据经验给出一个大致的范围，在范围中取一个最可能的值，这带有很大的模糊性。比如：本月的需求量在1.0 吨到1.5 吨之间，最可能的值是1.3吨。因此，本文引入了模糊变量，把需求设置为三角模糊数，将模糊不确定的需求转化为确定的数值。设需求最小值为三角模糊数的下界a，需求的最大值为三角模糊数的上界b，最可能需求量c为三角模糊数的中间值。因此，可以将客户i的需求通过三角模糊数表示为(ai,ci,bi)。

不确定变量的处理是一个较为复杂的问题，本文采用期望值处理模糊需求，相关理论见下文。不妨设A为三角模糊数，A=(a,c,b)，其中0 ＜a≤c≤b，其隶属度函数如下：

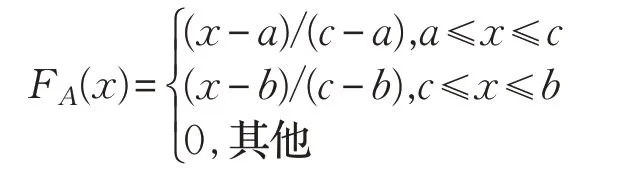
其中，a、b分别为三角模糊数的下限和上限，c为三角模糊数最有可能的取值，隶属函数图见图1。

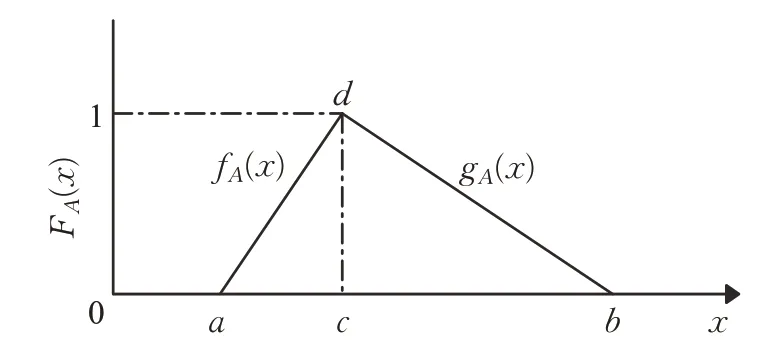
图1 隶属函数图

定义1[26]模糊数A的期望区间的中心称为这个数的期望值EV(A)，即：

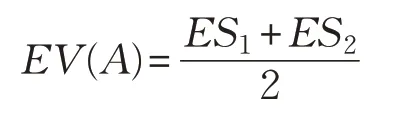
引理1[26]设A是边为fA和gA的三角模糊数A=(a,c,b)，区间随机集S∈RI(A)，那么：

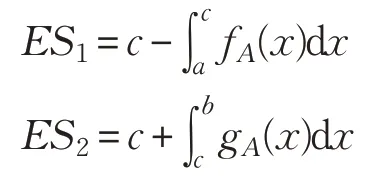
由定义1及引理1，本文得出如下推论。

推论 设A是边为fA和gA的三角模糊数A=(a,c,b)，则其期望值表示如下：

证明 由定积分的几何意义可知，ES1和ES2中的定积分部分分别为三角形Δacd和三角形Δdcb的面积，因此：

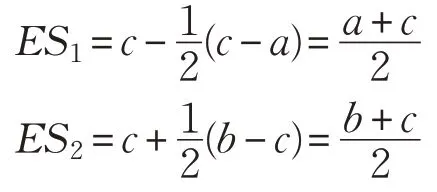
进而推得：

从而，将模糊需求量转化为期望值。

2.2 碳排放计算方法

直接测量碳排放量不太现实，通常人们根据油耗量估计碳排放量。根据Esteves-Booth等[27]研究表明，油耗量与碳排放成正比关系。假设CE为碳排放量，FC为油耗量，ε为燃油排放因子（单位油耗的CO2排放量），则可用公式表示为：

其中，不同燃料的燃油排放因子也不相同。本文参考欧洲碳排放计算标准，取ε=2.62 kg/L。

而车辆的油耗不仅与行驶距离有关，还与车辆的载重、速度、车型、路况、燃油类型、空气密度等有关。对此，考虑不同的影响因素也产生了多种不同的油耗计算模型。常见的油耗计算模型有：

（1）瞬时油耗模型[28]。该模型考虑了车辆的质量、性能、牵引力、空气阻力等因素，适用于车辆行驶距离较短、配送规模较小时的油耗计算。

（2）四阶段模型[29]。该模型根据车辆不同的行驶状态，分别建立了四种模式下的油耗计算模型——加速模式、减速模式、空转模式、漫游模式，将四阶段的油耗分别积分后求和即为总油耗。该模型计算较为精确，但依然只适用短途运输的油耗计算。

（3）综合模型[30]。该种模型对车辆参数进行了更为明确的考虑，如发动机转速、排量、摩擦系数，空气阻力系数等。因此，该油耗模型的计算结果精确度相对较高，具体模型如下：

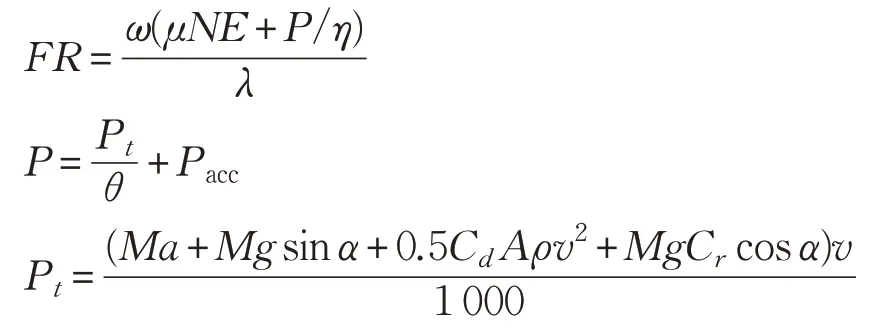
其中，FR为燃油消耗率；P为发动机总牵引功率；Pt为有效功率；ω是燃料与空气的质量比；μ为汽车发动机摩擦系数；η为柴油发动机的效率参数；λ为柴油热量值；N为发动机转速；E为发动机排量；θ为货车的传动效率；M为货车的总质量（空车质量+装载货物质量）；a为货车加速度；g为重力加速度；α为道路坡度；Cd为空气阻力系数；ρ为空气密度；A为货车迎风面积；v为车辆行驶速度；Cr为货车转动阻力系数；Pacc是货车其他功率需求，一般取0。各参数一般取值见表2。

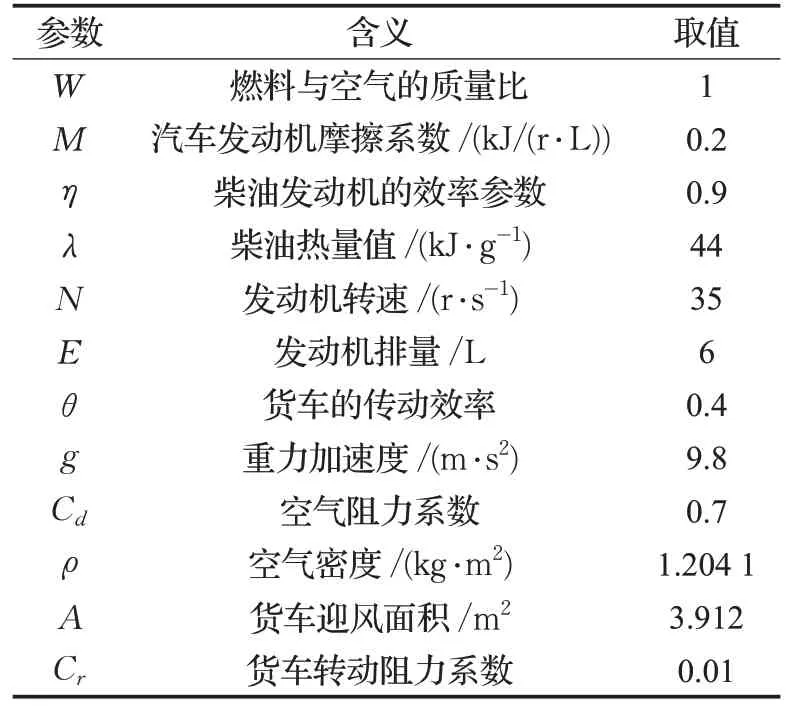
表2 模型参数值

综合上述三种模型，进行对比分析，综合模型的应用范围更广，计算结果也更为精确。故本文采用综合模型计算油耗量，进而计算碳排放量。

假设车辆从顾客点i行驶到顾客点j耗时tij，则油耗量计算公式为：

碳排放量计算公式为：

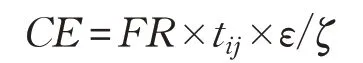
其中，ζ为单位转换系数（将g/s 转换为L/s），通常取值737。

2.3 数学模型

模型所需符号如下：

A：顾客和仓库集合，A={0,1,…,n}，其中0 表示仓库；

C：顾客集合，C={1,2,…,n}；

V：车辆集合，V={1,2,…,K}；

n：顾客数量；

Q：车辆最大负载能力；

Cs：单位时间的服务成本；

Cf：单位油耗费用；

qijk：车辆k访问完i后在访问j之前的载货量；

dij：顾客i与顾客j之间的距离；

ti：车辆对顾客i的开始服务时间；

si：车辆在顾客i的服务时间；

tij：从顾客i到顾客j的运输时间；

xkj：0-1变量，若顾客j由车辆k提供服务，则为1，否则为0；

xijk：0-1变量，若从顾客i到顾客j由车辆k提供服务，则为1，否则为0。

基于综合碳排放计算模型，考虑同时取送货问题相关约束，构建数学模型如下：

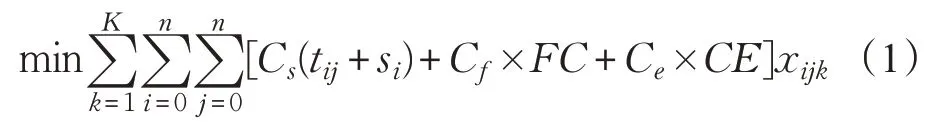
约束条件：

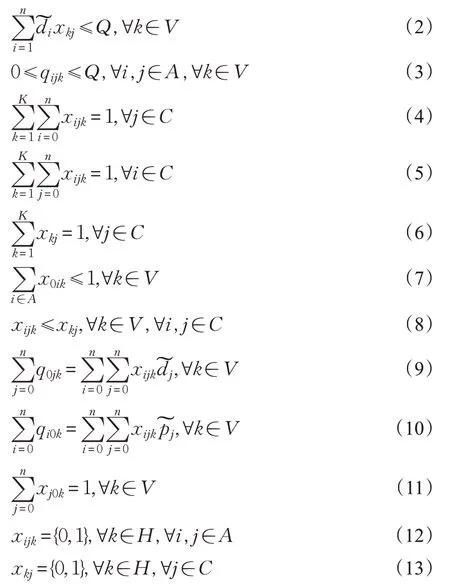
目标函数式（1）为总成本最低，包括服务成本（车辆租用费用、司机薪资）、油耗费用和碳排放费用。约束条件式（2）为车辆最大负载限制；式（3）为取货服务过程约束，保证每辆车在任何路段上的负载都不得超过车辆的最大负载限制，且非负；式（4）和（5）表示每个顾客有且仅有一次被服务；式（6）表示顾客j只能被同一辆车服务；式（7）表示每辆车最多只能使用一次；式（8）表示一辆车可以服务多个顾客，而一个顾客只能被一辆车服务；式（9）表示车辆从仓库出发时的载货量等于所服务的客户的送货需求量之和；式（10）表示保证车辆回到仓库的载货量为已服务的客户的取货需求量之和；式（11）表示车辆在完成任务后须回到配送中心；式（12）和（13）表示xkj和xijk为0-1变量。

3 算法设计

遗传算法是一种全局搜索机制，全局搜索能力强，但局部搜索能力较弱，一般只能求得次优解，而非最优解。而禁忌搜索算法为局部搜索机制，局部搜索能力强，具有极强的爬山能力，但对初始解依赖性较强。通过两种算法的融合，可以取长补短，优势互补。

3.1 解的表示与初始解

初始解的生成方式有两种——随机生成和启发式生成。启发式生成的初始解相对随机生成个体更为优良，但个体较为集中，易使算法陷入局部极值点。为保证个体多样性，使初始解尽可能地分布在整个解空间，本文采用随机生成的方式产生初始解。

本文采用自然数编码机制，具体编码方式如下：

假设有9 位顾客，3 辆配送车辆。首先生成一个客户的随机向量853762149，然后生成一个车辆的随机向量121312233，将两组向量相互对应，客户向量所对应位置的车辆向量值即服务该客户的车辆。即：第一辆车服务客户8、客户3、客户6，第二辆车服务客户5、客户2、客户1，第三辆车服务客户7、客户4、客户9，服务顺序依据随机客户向量中的先后位置进行。因此，解码后得到3条线路，车辆1为8→3→6，车辆2为5→2→1，车辆3为7→4→9。该编码方式保证了每辆车可服务多个客户，且只被安排一次，每个客户只由一辆车服务一次。

3.2 适应度函数

适应度函数的好坏关系到算法性能的优劣，一般通过求解适应度值来判别解的优劣，进而进行选择操作。鉴于VRPSPD 的特点，考虑到车辆的装载容量限制，为保证各路线总送货需求以及在各客户点取货后的负载不会超过车辆最大负载限制，避免产生不可行的路径，本文在适应度函数上增加了较高的惩罚代价。当车辆的载重量超过车辆容量时，每次都会有罚款。因此适应度函数如下所示：

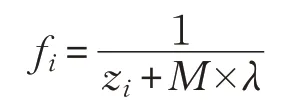
其中，zi为第i条染色体所对应的目标函数值，M是当车辆超载时所产生的足够大的惩罚成本，λ为超出的载重（当未超载时λ=0），fi为该染色体所对应的适应度值。计算目标值时考虑从配送中心出发及返回配送中心的旅途时间，并保证返回载货量与发车载货量分别与客户取送货总需求相等，以满足算法约束条件。根据适应度值来判断个体的优劣，进而使适应度值较高的个体存活下来，适应度值较低的个体死亡，即成本更高的解决方案将从种群中移除，而其他方案将保留下来。

3.3 选择算子

选择算子根据适应度值以一定的概率从旧个体中选择优良个体组成新种群。通常，该概率是由个体的适应度值与种群所有个体的适应度值之和的比例所确定的，适应度越高，被选中的概率也就越大。但是这种方法容易导致适应度高的个体大量繁殖，从而使算法的搜索范围过于局限。因此，本文采用改进的轮盘赌法[31]结合最佳保留策略进行选择操作。具体步骤如下：

步骤1 根据适应度值大小对种群进行排序，使适应度值最大的个体直接进入下一代。

步骤2 计算个体选择概率Pi=z(1-z)i-1，其中z=为种群中的个体数目。

步骤3 随机生成一个[0，1]之间的选择数x，计算个体i的累积概率：

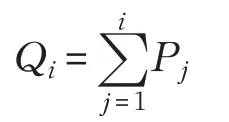
当累积概率为1 时，停止运算。此时，若Qi-1＜x≤Qi，则选择个体i。

步骤4 找出当前种群中适应度最优的个体与迄今最好个体的适应度值做比较，若当前最优个体适应度更优，则取代原最好个体。而被替换的原最好个体则取代当前种群最差个体。

步骤5 重复步骤3 和步骤4 共n次，选出新的种群为止。

3.4 交叉算子

交叉算子与算法的全局搜索能力密切相关，是遗传算法的主要算子，也是种群得以进化的基础。它模拟生物自然进化过程，使两条染色体互换部分基因，从而形成新个体。

本文采用两点交叉法。同时，为避免两个父代染色体相同的情况，采用了一种改进的交叉策略，以增加种群的多样性，如图2所示。具体步骤如下：

步骤1 根据交叉概率随机选出父代1 和父代2，并随机选取两个分界点c1和c2，两分界点之间即为交叉的基因片段。

步骤2 将第一个父代染色体的基因片段移到第二个父代染色体尾部，将第二个父代染色体移到第一个父代首部。

步骤3 对有误部分进行修正处理，删除染色体中重复冲突的基因。

3.5 变异算子

变异算子与算法的局部搜索能力密切相关，通过改变染色体上的部分基因位，形成新的染色体，从而维持种群的多样性，防止早熟早收敛的状况，进而提高算法的局部搜索能力。通常的变异操作有交换变异、倒位变异、插入变异等，但这些基本的变异操作对提高算法的局部搜索能力有限。而禁忌搜索算法有着独特的记忆能力，局部搜索能力强。故本文将禁忌思想引入遗传算法，采用禁忌搜索算法作为变异算子，进一步提高算法的爬山能力。本文采用λ-交换法[32]构造邻域函数，确定藐视准则为当某个基因移动产生的解优于当前最好解时，则不论该基因移动是否处于禁忌状态，都接受该移动，并将其作为新的当前解。具体步骤如下：

图2 交叉流程图

步骤1 确定禁忌算法的初始解，选择交叉操作后生成的较优解作为初始解X。

步骤2 邻域结构设计：用邻域函数为X产生若干邻域解，并从中确定候选解集。

步骤3 判断候选解集是否为空？若否，则选出候选解集中的最优解S，转步骤4；若是，则进入下一轮迭代。

步骤4 判断S是否满足藐视准则？若满足，则令X=S，并将S加入禁忌表；若不满足，则转步骤5。

步骤5 判断S的禁忌属性。若S属于禁忌表，则删除S，回到步骤3；若不属于，则令X=S，并将S加入禁忌表。

步骤6 令迭代次数gen=gen+1，并进入下一轮迭代。

本文将禁忌搜索的思想融入遗传算法，从而提高遗传算法的局部搜索能力，遗传禁忌搜索算法具体实现流程如图3所示。

4 案例分析

图3 算法流程图

案例分析部分，引入了三角模糊数来描述客户的需求，使其更符合实际，并对计算结果进行了分析。然后，通过不同算法进行比较，验证了模型的合理性和算法的有效性。所有启发式算法都是在华硕W518 计算机上使用MatlabR2012a执行的，具体配置为1.70 GHz Inter®CoreTMi5-4210U处理器，4 GB内存，64位Windows 8操作系统。本案通过Matlab 随机生成了30 个客户点，客户的需求量基于三角模糊数确定。表3 给出了顾客位置坐标、服务时间、取货量及其送货需求。根据实际情况，决策者确定6 辆车重为2.5 吨，载重量为6 吨的卡车，行驶速度设为60 km/h。成本部分包括了服务成本（车辆租用费用、司机薪资）与运输成本（油耗费用、碳排放费用）。一般情况下，服务成本为90 元/h。查询最新柴油价格为6.5 元/L，碳排放价格为0.6 元/kg。

4.1 田口法参数设置

算法对于参数的设置非常敏感，不同的参数值能决定算法的有效性，因此需要在运行算法之前确定合理的参数值。遗传算法作为一种元启发式算法，参数设置包含迭代次数、种群大小、交叉概率、变异概率等。依据以往遗传禁忌参数设置经验[18-19]，本文交叉概率设置为0.85，变异概率设置为0.15。算法的最优迭代次数与种群大小，本文采用田口设计的实验方法进行参数调优，以确定其值。田口法是一种优秀的参数校准方法，近年来被许多研究人员所采用。Taguchi 定义了信噪比(S/N)作为变化的度量，这种转换方法也使该参数设计具有很好的鲁棒性。此外，田口法的目标值分为“越小越好”“越大越好”“名义上最好”三组。由于决策者的目标函数是成本最小化，因此本文选择“越小越好”的类型，所对应的信噪比由Mousavi和Niaki[33]给出，如下：

式中，n为各参数水平上算法的执行次数，Ft为响应值，即第t次实验的目标函数值。

设置种群大小分别为10、20、30、40、50，迭代次数为100、200、300、400、500，每种类别分别进行10 次实验，共进行250 次测试。随后，创建田口设计，并将产生的250个总成本实验值作为响应值进行田口设计分析。分析结果如表4所示，相应的信噪比和均值如图4、图5所示。从图4 中可以看出，当种群大小为40，迭代次数为500时，信噪比最大。同样，在图5中，当种群大小为40，迭代次数为500 时，总成本均值最小。因此，根据田口实验分析所得，参数种群大小设置为40，迭代次数为500次。

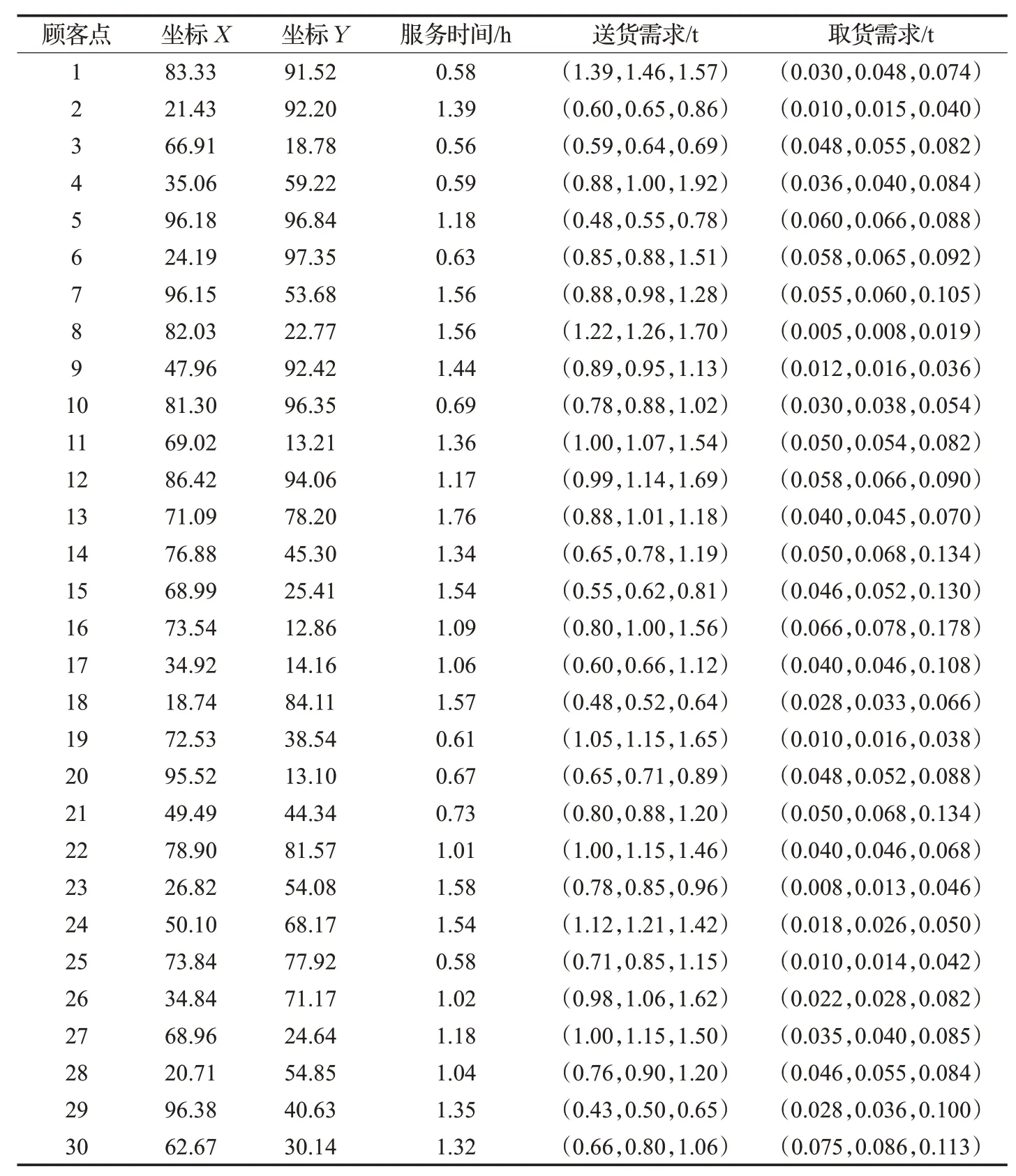
表3 顾客信息表

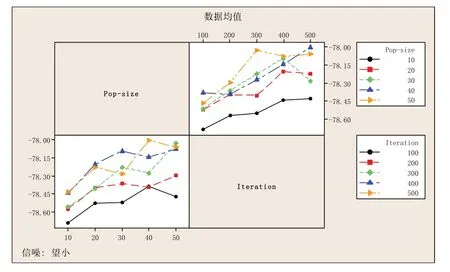
图4 信噪比交互作用图

4.2 计算结果分析

基于上述数据，运行算法30次，得到求解结果中最好的一次路径优化结果。总成本最小为7 525.3 元、油耗量为254.74 L、碳排放量为667.41 kg，具体求解结果如表5所示，最优路径如下：

图5 均值交互作用图

车辆1：22→9→26

车辆2：3→11→17→30

车辆3：4→23→6→2→18→28

车辆4：21→16→27→19→8

车辆5：29→13→24→5→12→14

车辆6：1→10→25→7→20→15

一般情况下，旅行时间越长，总成本越高。然而，对比车辆1 与车辆2 却发现，车辆1 的旅行时间少于车辆2，而总成本却高于车辆2。不仅如此，车辆1 服务的客户数最少，旅行时间最短，但油耗量与碳排放量却相较于车辆2、3、4都要高。这是由于车辆1在客户点的总服务时间相对较短（占总旅行时间45.42%），而车辆2、3、4 的总服务时长分别占总旅行时间54.99%、64.52%、56.75%。因此，车辆1 在路上的行驶时间就相对较长，为4.17 h，车辆2 的行驶时长为3.52 h，车辆3 的行驶时长为3.74 h，车辆4的行驶时长为3.94 h，这就导致车辆1的油耗量与碳排放量反而高于车辆2、3、4。因此得出，车辆的总旅行时间与油耗量并非单纯的线性关系。在解决带碳排放的车辆调度问题时，不仅要考虑车辆的租用时间，也要考虑车辆在各客户点的服务时间（卸货、取货等）所带来的影响。

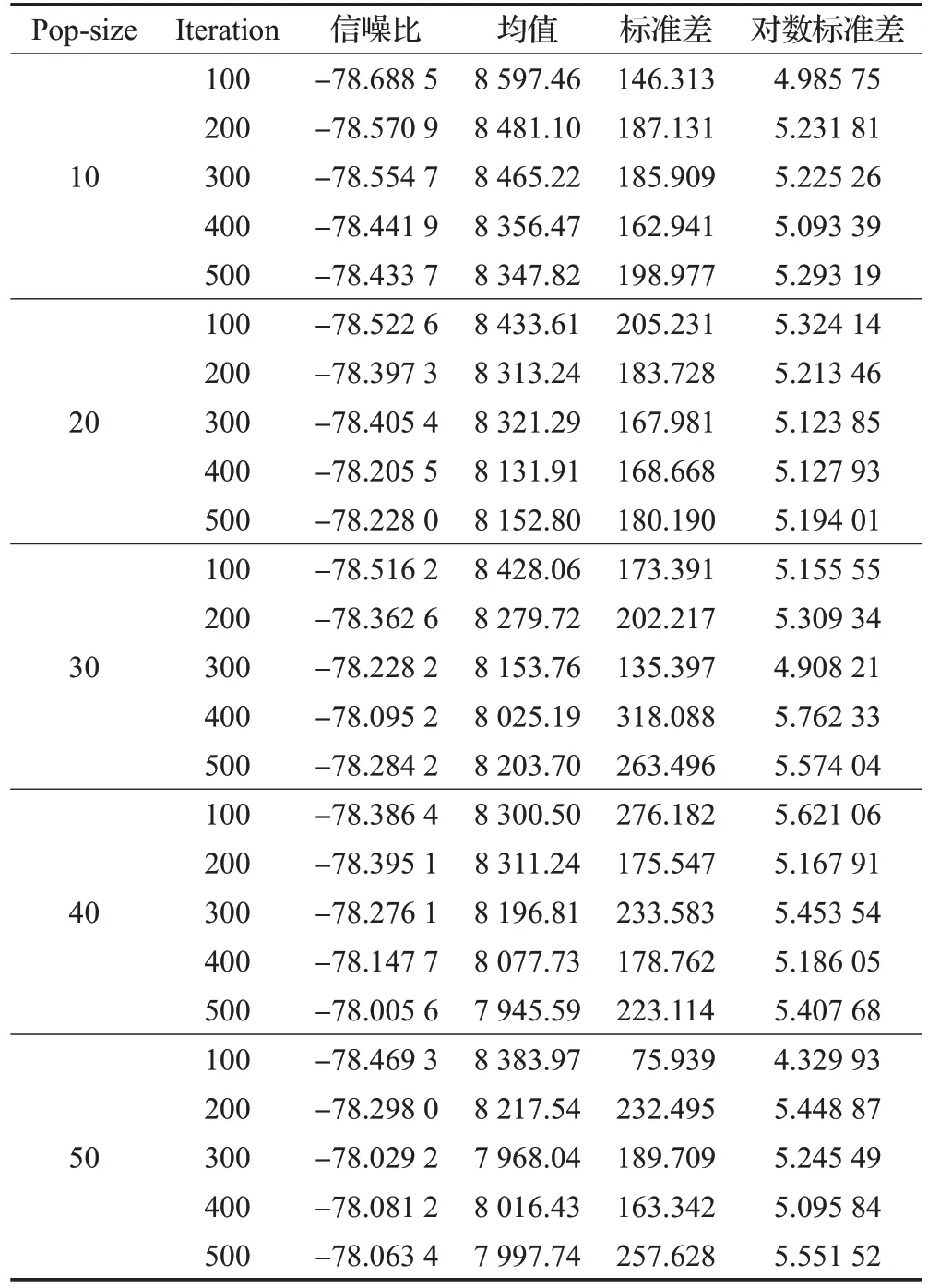
表4 田口设计分析结果

最后，从服务各客户的载重变化情况来看，出库载重均未超过车辆的允许载重，且车辆3、4、5、6的出库荷载都充分使用了车辆的装载能力，体现了该算法的有效性。

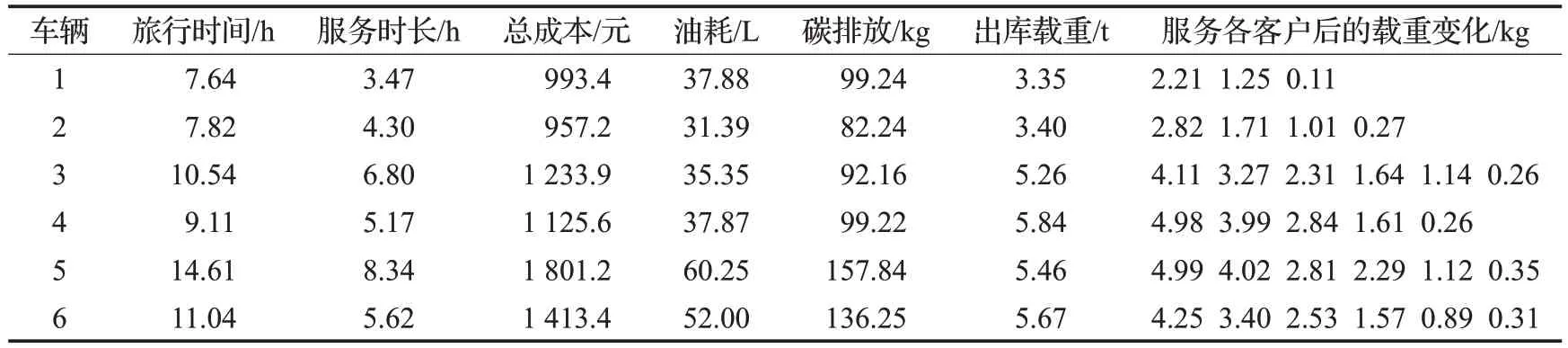
表5 最优解结果

4.3 算法对比分析

为验证改进的遗传禁忌算法对于求解模糊需求下绿色同时取送货车辆调度问题的性能，本文针对三种不同的案例规模，分别利用遗传算法、粒子群算法对本模型再次进行求解，对比分析算法的求解效果。各算法参数设置如表6 所示，其中P为种群大小，G为迭代次数，CP为交叉率，MP为变异率，TG为禁忌代数，CS为候选集，TL为禁忌长度，W为惯性权重，C为加速因子。每种算法运行30次，分别取各算法所求最优解，并给出三种算法迭代效果图。

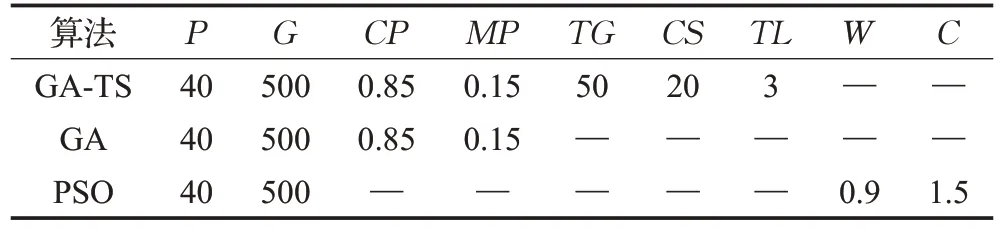
表6 算法参数设置

不同案例规模下算法计算结果对比如表7、表8、表9所示，算法迭代效果对比如图6所示。

表7 30个客户算法计算结果对比

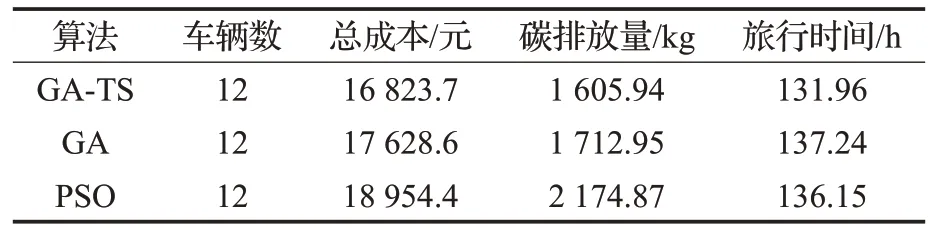
表8 60个客户算法计算结果对比

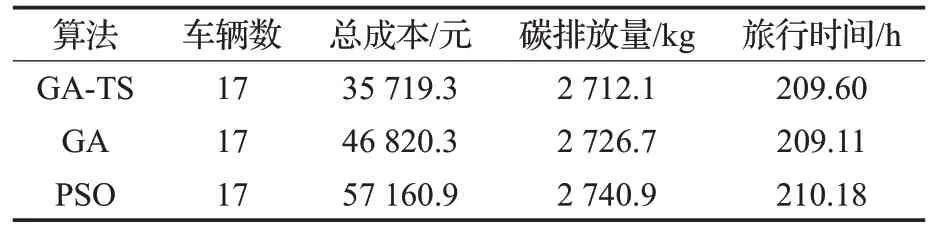
表9 90个客户算法计算结果对比

当客户数量为30 时，从表7 中可以看出，本文算法的最优解相较于传统遗传算法而言，可使总成本降低1.6%，碳排放量降低2.2%，总旅行时间减少0.82 h；相较于例子群算法而言，可使总成本降低3.4%，碳排放量降低5.0%，减少总旅行时间1.71 h。

图6 算法迭代对比图

当客户数量为60 时，从表8 中可以看出，本文算法的最优解相较于传统遗传算法而言，可使总成本降低4.8%，碳排放降低6.7%，总旅行时间减少5.28 h；相较于粒子群算法可使总成本降低12.7%，碳排放量降低35.4%，总旅行时间减少4.19 h。

当客户数量为90 时，从表9 中可以看出，本文算法的最优解相较于传统遗传算法而言，可使总成本降低31.1%；相较于粒子群算法而言，可使总成本降低60.03%。对比碳排放与旅行时间，三种算法的差别不大。另外，经过验算发现，当客户数量为90 时，总成本高于正常水平，这是由于车辆的载重超过车辆容量限制，从而产生了较高的惩罚成本，此种情况下可考虑用不同的车型安排取送货，这将是下一步的研究方向。

综上，当客户为小规模及中等规模时，本文算法求解模糊需求下绿色同时取送货问题的求解效果均优于GA 和PSO。当客户规模较大时，本文算法的求解效果仍远优于GA 和PSO。且从图6 可以看出，粒子群算法的收敛速度最快，但结果最差；遗传算法的求解结果优于粒子群算法，但是收敛速度较慢；改进的遗传禁忌算法的求解效果最好，收敛速度仅略低于粒子群算法。故而，认为改进的遗传禁忌算法对于求解该问题是实用且有效的。

5 结束语

本文以VRPSPD为基本模型，考虑了客户需求的不确定性以及客户服务时间，引入了综合碳排放计算方法，建立了模糊需求下的绿色同时取送货模型，并提出了一种求解该问题的遗传禁忌搜索算法。通过案例分析验证了模型和算法对于处理模糊需求下的绿色同时取送货车辆调度问题的可行性和有效性。结果表明，车辆的总旅行时间与油耗量并非单纯的线性关系，需要考虑车辆在各客户点的服务时间。同时，改进的遗传禁忌搜索算法在求解小规模及中等规模客户量时，求解效果及收敛性均优于传统的遗传算法和粒子群算法。当客户规模较大时，改进的遗传禁忌搜索算法对于总成本的求解效果仍远优于传统的遗传算法和粒子群算法。本文以低碳作为研究目标，建立的模型及求解算法对于物流企业在绿色可持续发展的背景下进行物流配送提供了优化支持，也为政府相关部门制定节能减排政策提供了一些参考和借鉴。

当然本研究还存在许多不足之处，比如没有考虑客户的时间窗要求，以及根据客户规模和客户需求选用不同的车型，这些将是下一步研究的方向。