从车牌识别数据中提取有效旅行时间算法研究

王 晰，袁绍欣

长安大学 信息工程学院，西安 710064

1 引言

车牌识别系统目前在城市交通中得到了广泛应用，已经成为获取车辆交通旅行时间的一个重要数据源[1]。系统利用设置在城市道路上的卡口摄像机，对经过车辆进行车牌号码识别、车牌颜色识别、位置记录、时间戳记录和速度计算，从而实现对超速和闯红灯等交通违法行为的监控。此外，根据车辆依次经过的两个卡口的时间戳可计算得到车辆在两个卡口间路段的旅行时间观测点[2]，以下简称ANPR（Automatic Number Plate Recognition）数据。相对于具有路网覆盖能力但采样精度低的车辆GPS 数据而言，ANPR 数据可形成采样精度高、数据量大的研究样本，并可通过车牌颜色区分车型，这对于城市管理者评价道路通行能力以及出行者的出行决策都非常重要[3]。

ANPR 数据中的少量数据往往因明显偏离大多数数据而被视为噪音数据，相应地大多数的数据被视为有效数据。与由设备产生的异常数据不同，这些噪音数据都是真实的车辆旅行时间数据。实时采集的ANPR 数据中的噪音数据通常由不能代表特定时空下交通状况的数据组成。例如，少数私家车会因不熟悉道路路况而缓行；空载出租车因寻客而缓行；少数车辆在两个卡口间因各种原因存在临时停车行为而导致其旅行时间过长；少数公交车在个别站点停留时间过长；因偶发的恶劣天气、交通事故或红绿灯故障等造成特定路段个别时段车辆的整体缓行。此外，当采集的ANPR数据存档形成历史数据后，其中的噪音数据还要包括不能代表特定时空下通常交通状况的观测点，例如在某一时间段通常拥堵的路段在个别天非常通畅，从而使车辆旅行时间较通常短，反之亦然。识别和滤除ANPR历史数据中的噪音数据后，得到的有效数据可以表征特定时空下大概率可重复发生的通常交通状况，因而进行这方面的研究很有意义。

2 相关研究工作

对ANPR 数据中的噪音数据进行识别并提取有效数据的相关研究，因ANPR 数据应用环境和场景的不同，研究方法也有所不同。

实时的交通控制系统，如Transguide[4]、TranStar[5]等，需要识别并滤除不代表交通状况的ANPR 噪音数据，从而根据有效数据准确评估路段的交通状态并给出控制措施。这些系统中的算法针对交通状态在时间上具有连续性变化以及ANPR 观测点通常具有的正态分布的特点，将系统控制时间划分为连续时间窗口，利用前一个时间窗口中的旅行时间数据或指标计算得到当前时间窗口用均值和标准差表示的有效数据范围，范围外的过大和过小的数据将被视为噪音数据，如此循环往复就可实现噪音数据的连续识别和清除。但当交通状态产生突变时，上述方法对噪音数据的识别不理想，为此Dion 等[6]将突变交通状态下的ANPR 观测点设定为遵从对数正态分布来确定有效数据范围，取得对噪音数据的良好识别效果的同时也增强了算法处理这类数据的鲁棒性。

将ANPR 历史数据中的噪音数据和有效数据区分开来，往往需要将有效数据和噪音数据视为不同种群。这是因为比例较少的噪音数据在ANPR 历史数据中通常呈现出稳定的右向尾部分布特点，而比例较大的有效数据则由于旅行时间的可变性呈现出单峰、偏斜乃至多峰形态。因而基于它们在分布上的各自特征进行分布拟合和相应的数据聚类来加以区分是常用的研究方法。Kieu等人[7]研究比较了高斯分布、对数正态分布、伽马分布、韦伯分布和布尔分布，认为对数正态分布对旅行时间具有很好的分布拟合效果。Rakha 等人[8]和Emam等人[9]的研究也得到了类似结论。Kazagli等人[10]通过使用两个对数正态分布的混合模型分析了近10个月ANPR数据样本，对其中无停车行为和有停车行为的两类数据进行分布拟合，同时实现相应的数据聚类加以区分。但该研究关注的有停车行为观测点仅是噪音数据中具有较大值的一类，因此研究者用10 个月的数据叠加在一起来增强右向长尾特征，同时这也导致了有效数据的可变性变得不突出——更多地呈现单峰形态，这也是该研究用两个对数正态分布的混合模型进行分析的合理之处。但是如果以月或星期为规模进行数据叠加（不同规模的数据从不同层次反映通常交通状况特征），数据样本量的降低可导致有效数据的形态不一定能保证单峰形态，即有效数据也存在多种群，同时也会导致噪音数据尾部分布的长度缩短或不明显，这为二类数据的区分带来了困难，因而有必要提出算法，提升对ANPR 历史数据中噪音数据识别的鲁棒性和有效数据可变性的处理能力。

3 问题陈述

（1）旅行时间可变性导致有效数据和噪音数据的区分阈值和种群数量难以界定。一天不同时间段因交通状态的多样性（通畅、拥堵和堵塞）导致不同时间段的旅行时间（为有效数据）可变，因而有效数据和噪音数据之间很难用固定的阈值加以区分[11]。此外，不同天的同一时间段的旅行时间也会因为交通状态的不同而具有可变性，即多种群特点，从分布上表现为偏斜或多峰形态。因而用两个分布的混合模型来区分带有多种群特点的有效数据与噪音数据两类数据并不合适。

（2）ANPR数据样本质量欠佳情况下有效数据提取的鲁棒性问题。噪音数据具有分布上的右向尾部以及比例少的特点，这是区分两类数据的主要参考依据，但ANPR数据样本在数据量比较少时，噪音数据的这个特点可能并不突出。因此如何设计算法可以同时很好地识别噪音数据特点明显和不明显的数据样本是需要解决的问题。

4 ANPR样本有效数据提取算法

4.1 数据样本的选取和噪音数据的初步过滤

将一天时间以30 分钟为间隔分为48 个时间段，根据起始卡口通过车辆的时间戳，将ANPR数据划分为48组数据样本。估计一个旅行时间经验阈值π（一般为高峰期间车辆平均旅行时间的2～3 倍），其值将确保各组样本都能包含所有的有效数据和一定量的噪音数据。大于π的观测点数据将从所有样本中作为噪音数据被滤除。

4.2 具有K 个密度分支的对数正态分布混合模型

式（1）是对数正态分布混合模型，它用K个对数正态分布的密度分支所组成混合密度f(yi|θ)来拟合形状通常不规则的数据样本概率密度曲线。

K最小值为2 意味着至少用两个密度分支来对数据样本的分布进行拟合，以体现大部分数据样本中都至少包含有效数据和噪音数据两个种群；K大于2意味着同一时间段不同天可能存在多个交通状态，从而导致有效数据也具有多种群。yi为数量为N的数据样本中的第i个观测点。ηk(η1+η2+…+ηk=1,0＜ηk ＜1)是密度分支混合比例。需要评估的参数θ=(η1,η2,…,ηk,为分布参数。

模型参数θ需要通过EM（Expectation Maximization）算法[12]来估计。算法包含E 和M 两个步骤。通过E 步骤评估得到的后验概率（样本中第i个数据在t次迭代隶属于第k个分布的概率），如式（2）所示：

M步骤利用评估θ参数：

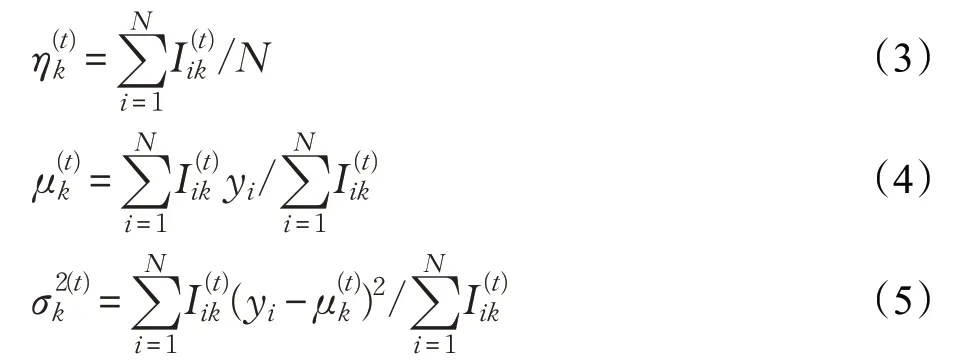
EM 两个步骤交替进行直到θ参数收敛。再根据式（2）中的Iik可以判断出yi所属的密度分支。因而对K个密度分支进行参数估计的同时，也将数据样本聚类为K组，即K个种群。

4.3 有效数据分布模型与噪音数据的分布模型

式（1）可转为式（6）的形式，表示对数据样本分布的拟合可表示为有效数据分布的拟合和噪音数据分布的拟合。

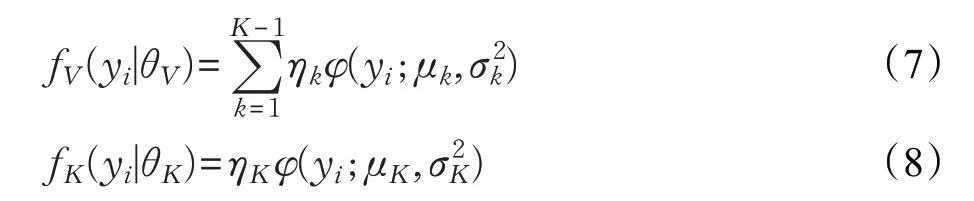
其中，fV(yi|θV)表示由一个或多个密度分支组成的有效数据密度。fK(yi|θK)用一个密度分支表示具有稳定的右向尾部特点的噪音密度。fV(yi|θV) 和fK(yi|θK) 在(0,π)内可能存在一个交叉点或多个交叉点，设x为具有最大横坐标交叉点的横坐标值，则(0,π)区间被分为(0,x)和 (x,π)两部分。

4.4 噪音数据密度分支的三个特征

K个密度分支中代表噪音数据密度的分支具有如下三个有异于有效数据密度分支的特征。

（1）噪音数据在分布上呈现右向尾部特点决定了噪音密度分支fK(yi|θK)的分布参数σK应是所有密度分支中最大的，如式（9）所示：

（2）fK(yi|θK)的比例需要遵循式（10）以体现噪音数据比例少于有效数据的特点。

（3）噪音数据在分布上呈现的右向尾部特点也决定了在 (x,π)区间f(yi|θ)的右向尾部主要由fK(yi|θK)拟合而成，它们的拟合优度用R2指标度量，见式（11），该值介于0 和1 之间，越接近1 表示拟合效果越好。应好于任一有效数据密度分支与f(yi|θ)的拟合优度(k ＜K)，如式（12）所示：

其中，表示在 (x,π)区间内fK(yi|θK)和f(yi|θ)直方图中各对应直方条值差的平方和，而表示在(x,π)区间与f(yi|θ)各直方条值与它们平均值差的平方和。

上述三个分布特征也是判断数据样本质量欠佳的依据，即数据样本较为稀疏时，噪音数据在分布上的右向尾部特点不明显，从而导致式（9）、式（10）、式（12）不能同时成立。此时可将数据样本小于第10 百分位（过快观察点）和大于第90 百分位（过慢观察点）的数据视作噪音数据[13]。

4.5 使有效数据和噪音数据取得最佳分离效果的密度分支数量K 值判据

判据1 在(0,x)内，寻找K=O，使fV(yi|θV)与f(yi|θ)拟合优度R2K取得最大值，即fK(yi|θK)与fV(yi|θV)重叠部分最小——fK(yi|θK)对f(yi|θ)影响最小，如式（13）所示：

其中,为在 (0,x)区间fV(yi|θV)和f(yi|θ)直方图中对应直方条值差的平方和，而表示在(0,x) 区间f(yi|θ)各直方条值与它们平均值差的平方和。

判据2 在(0,x)内，当与1 的差值达到一个可接受的ε时，相应的K值可认定为最佳值。

4.6 算法实现

步骤1 设置K=2,ε=0.03,π=4 200 s。

步骤2 将ANPR数据分成48个数据样本并进行噪音数据的初步过滤。

步骤3 用EM算法将样本数据分为K个具有对数正态分布的聚类组，将满足式（9）、式（10）、式（12）的密度分支标识为噪音密度分支，否则转到步骤6。

步骤5 得到K=O个密度分支以及相应数目的聚类组，根据Iik识别噪音数据并滤除，剩下的数据则为有效数据，转到步骤7。

步骤6 提取数据样本中介于第10百分位和第90百分位之间的数据为有效数据。

步骤7 计算有效数据平均值和标准差等统计指标。

算法在带Mixmod软件包[14]的Matlab平台上实现。

5 案例研究

5.1 数据源描述

案例选取西安市咸宁路和友谊路自西向东方向两组卡口之间的路段（如图1所示），长度分别为3.8 km和1.8 km。这两个路段是西安市流量较大的主干道，各包含三个信号交叉口，沿线有居民区和商业区，在两个卡口间车辆出现临时停车以及缓行等现象较为常见。所用数据采集于2014年3月，车型为车牌为黄色拥有专用车道的公交车以及车牌为蓝色的非公交车（主要为私家车和出租车）两种。

图1 研究选用的两个路段

5.2 数据实验及分析

图2展示了咸宁路公交车和非公交车6：00至22：00期间的旅行时间观测点，横坐标为车辆经过起始卡口的时刻点，纵坐标为车辆经过两个卡口所在路段的旅行时间。观测点可分为密集区域以及分散区域两部分，分散区域观测点可视作噪音数据。从图2（a）和图2（c）可以看出，公交车噪音数据比较稀疏且个别时段甚至缺乏噪音数据，而图2（b）和图2（d）各时间段的噪音数据都比较丰富。

图2 选用路段公交车和非公交车旅行时间观测点

图3 以咸宁路非公交车18：30—19：00 数据样本为例，展示了算法提取有效数据的过程。图3（a）中，用K=2 个对数正态分布对数据样本进行分布拟合和数据聚类，在旅行时间(0,x)范围内，有效数据的密度曲线与混合密度曲线的拟合优度0.946＜0.970，即两个密度曲线拟合程度没有达到设定水平，噪音密度分支影响依然很大。因此在图3（b）中用K=3 个对数正态分布对数据样本进行分布拟合和数据聚类。在旅行时间(0,x) 范围内，有效数据密度曲线和混合密度曲线的0.997＞0.970，即有效数据密度曲线和混合密度曲线拟合程度比较好，噪音数据密度分支影响已经很小，有效数据和噪音数据在K=3 时取得了较好分离效果。图3（c）展示了噪音数据被滤除后的有效数据直方图，隶属于噪音密度分支的数据可近似看作旅行时间大于x的观测点，实际区分方法依据式（2）进行。上述过程中，在(x,4 200)范围内，被认定的噪音密度分支曲线（相比任一个有效数据密度分支曲线）与混合密度曲线始终保持了最好拟合效果。

图3 咸宁路非公交车18：30—19：00有效数据提取

图4 展示了研究的算法对咸宁路公交车18：30—19：00数据样本提取有效数据的过程，当K=2 时，0.989＞0.970。有效数据密度曲线和混合密度存在两个交点并取得了较好的拟合效果。此时提取的有效数据可近似地看作介于这两个交点间的观测点，实际区分方法依据式（2）进行，噪音数据相应地也被分为过快和过慢两种类型。

图5 展示了算法对两个路段公交车稀疏噪音数据和非公交车密集噪音数据都具有良好的识别效果，此外还判别出咸宁路公交车在12：30—13：30、14：00—14：30、15：30—16：00 以及 20：30—21：00 时间段，友谊路公交车在07：30—08：00、19：00—19：30、21：00—22：00 时间段内的数据样本缺少噪音右向尾部特点，提取数据样本中介于第10 百分位和第90 百分位之间的数据为有效数据。

图4 咸宁路公交车18：30—19：00包含过快和过慢两种噪音数据

图5 旅行时间噪音数据的识别及对均值的影响

从图5还可以看出：非公交车各时间段有效数据平均值明显小于滤除噪音数据前的所有数据平均值，这意味着数量较少的噪音数据具有很强的干扰作用。相比之下，公交车噪音数据对数据平均值影响并不明显，这不仅因为公交车样本数据中噪音数据量较少，而且多个时间段过快和过慢的噪音数据对平均值的影响具有相互抵消的效果。

图6 对比了研究路段有效数据提取前后公交车与非公交车旅行时间的均值和标准差（图中公交车有效数据均值可近似看作滤除噪音前的数据均值）。

在图6（a）中的大部分时间段内，咸宁路公交车滤除噪音数据前的平均旅行时间都小于非公交车，友谊路在8：30—18：00 时间段内的大部分时段也是如此，这明显有违常识，因为公交车在站点上下客停留时间通常会使其旅行时间高于非公交车。而去除噪音数据后，咸宁路在大部分时间段内非公交车的平均旅行时间要小于公交车（晚高峰17：30—19：00期间除外，该时间段公交车因具有专用车道而使其旅行时间小于处于拥堵中的非公交车）。友谊路公交车和非公交车平均旅行时间也有类似关系。另外滤除噪音数据前，非公交车的旅行时间标准差明显比公交车旅行时间标准差偏高，而滤除噪音数据后，差距则没有那么明显。由于旅行时间平均值代表了出行的平均成本[15]，标准差代表了出行者到达目的地的旅行时间可靠程度。如果对ANPR 数据不经过有效数据提取就直接进行平均值以及标准差的计算，得到结论对于出行方式决策必然产生误判。

图6 公交车和非公交车有效数据提取前后的统计值

5.3 实验对比

图7 是用K-Means 算法对每半小时观测点数据聚为两类的效果图，从图中可见，不仅很多稀疏观测点没有被识别为噪音数据，而且提取的有效数据也没能体现出在一天不同时间段应有的可变特征。而在图5（b）中，应用“ANPR样本有效数据提取算法”，除了08：00—08：30和18：30—19：00 时间段的数据被聚为三类外，其他时间段的数据也聚为两类，但却取得了对噪音数据的良好识别效果以及使有效数据呈现出在一天不同时间段应有的可变特征。这种对比效果意味着欧式距离不是对这两类数据进行聚类的有效依据。“ANPR 样本有效数据提取算法”从“比例较少的噪音数据在分布上通常呈现出稳定的右向尾部特点”直观感知出发，用对数正态分布混合模型对噪音数据右向尾部特征和有效数据多种群可变性进行建模，并用提出的两个判据确保两类数据具有最佳的分离效果。这种将观察特点和定量分析紧密结合的方法确保了算法在提取有效旅行时间数据方面的合理性和有效性。

图7 K-Means算法识别咸宁路非公交车噪音数据

6 结束语

ANPR 系统中的有效数据代表特定时空下的通常交通状况，为排除样本中不代表通常状况的噪音数据，本文研究工作的主要贡献为：

（1）提出了ANPR样本有效数据提取算法。该算法用K个对数正态分布混合模型针对噪音数据的右向尾部分布以及比例少的特点进行建模，依据噪音数据的三个分布特征从K个密度分支中识别噪音密度分支并对数据质量进行判断。对于噪音数据特征明显的样本给出了使有效数据和噪音数据具有最佳聚类效果的分布数量K值判据；对于质量欠佳的样本，则将第10百分位和第90 百分位之间的数据视为有效数据，不仅解决了因旅行时间可变引起的有效数据和噪音数据的区分阈值和种群数量难以界定的问题，同时增强了算法提取有效数据时的鲁棒性。

（2）针对西安市咸宁路和友谊路选用路段上收集的公交车和非公交车ANPR数据，算法实验取得了良好的噪音数据识别效果，同时也说明了ANPR数据中的噪音数据会影响旅行时间统计结果的精确度，不滤除噪音数据会对两类车通常交通状况下的运行状态产生误判。