结合深度学习的短时车流量预测优化方法

王 钰，郭兰英，程 鑫

长安大学 信息工程学院，西安 710064

1 引言

在智能交通的发展历程中交通流量预测起着重要的作用。精确和实时的交通流预测能够用来分析道路规划，减少交通事故伤亡，提供合理的出行意见[1]。对不同的重要交通路口的车流量短时间段进行预测，得到尽可能准确的预测结果，可以为相关部门的交通管制和广大居民的出行提供及时有效的参考，缓解不同时刻交通压力，在极大限度下充分利用道路资源。

目前为止，已经有大量的方法被应用到短时交通流的预测之中。短时交通流量的预测分为参数模型和非参数模型。参数模型包括自回归移动平均模型（Autoregressive Integrated Moving Average，ARIMA）[2]和卡尔曼滤波[3]等。非参数模型包括KNN（K-Nearest Neighbors）[4]、SVR（Support Vector Regression）[5]、人工神经网络[6]等。

由于短时车流量的变化呈现出一定的非线性特征，且随着时间变化这种非线性模型也十分灵活，为了能够更好地拟合较为复杂的数据，近年来更加关注于各种非线性预测模型。Oh 等[7]提出了基于KNN 的新的序列搜索算法来预测交通状态，该方法和传统方法相比，显著提高了预测的准确性、效率和稳定性。丁栋等[8]基于影响模型，将交通网络中每个节点当作一个马尔科夫过程，整个网络看成是多个马尔科夫交互过程，再用EM算法训练得出模型参数，从而预测短时交通流。文献[9]首次提到了用回归树和随机森林模型预测城市工作区域的车流量，并与神经网络和KNN 预测模型进行比较，结果显示随机森林具有更高的预测准确度。但文献中只分析了一个大的区域的车流量预测问题，并未具体分析各路段的车流量预测问题，且没有对随机森林的超参调节和优化进行讨论。支持向量机（Support Vector Machine，SVM）是一种通过寻求结构化风险最小来提高泛化能力的模型，解决了一般算法难以解决的非线性、高维识别、过学习的问题，但是SVM 模型在对大规模训练样本求解二次规划时会涉及到高阶矩阵的计算，此时矩阵的存储和求解会占用计算机的大量内存，对硬件的要求比较高，而且传统的支持向量机只能作二分类法，而无法处理实际应用中遇到的多分类问题。孟飞等[10]通过定义粒子群聚拢度使其服从随机分布，使得粒子群算法避免了陷入局部最优解，并使用被该算法优化过参数的小波神经网络对车流量进行预测，证明了这种组合优化算法的预测精度高于两种单一算法。王洪德等[11]通过总结灰色系统不需要大规模原始数据的优点和支持向量机良好的泛化能力，将灰色系统与支持向量机进行了组合，将其应用于地铁客流量的预测上，取得了相对误差仅3.61%的实验结果。但灰色系统经过累加合成之后就会失去有用的规律，而且在建模过程中没有结合数据背后真正反映的特征与规律。文献[12]首次在车流量预测中使用了深度学习模型，并结合多任务学习的方法预测整条道路的车流量，取得了较常见模型更好的预测准确度，但该文献中使用的是较早的基于受限玻尔兹曼机（Restricted Boltzmann Machines，RBM）的深度置信网络（Deep Belief Network，DBN）。深度网络结构由具有关联关系的多个隐含层组成，使用神经网络的隐层参数作为深度网络新顶层预训练初始化参数，映射上一个图层的输出得到抽象的输入表示[13]。杨志勇[14]通过改进神经网络的权值修正函数与学习率的调整方式，将其应用在交通流量预测上。实验结果表明，在交通流量预测上使用由灰色系统与神经网络组合的模型的预测精确度在一定程度上要高于两种单一模型预测的精确度。

深度学习模型如深信度网络[15]、堆叠自动编码器[16]、LSTM（Long Short-Term Memory）递归神经网络[17]已经用于车流量预测。但用LSTM 进行车流量预测时并未考虑到多种因素的影响及处理方法。为了能够更加准确地预测短时交通车流量，本文提出了一种对车流量多种因素处理的Classify 方法，结合深度学习的LSTM递归神经网络对短时车流量进行预测，然后对结果进行误差分析，提高了预测的精度。

2 结合深度学习的短时车流量预测优化方法

为了提高短时车流量预测的准确度，本文考虑了多种因素，如天气、节假日等的影响，提出了一种对车流量多因素处理的Classify 方法，然后通过Long Short-term Memory 神经网络对车流量数据进行训练预测，取得了更佳的效果，能够更好地应用到城市路口、收费站等重要交通要道的车流量预测。

2.1 数据描述

本文依据陕西省高速公路收费站现场调查和历史真实数据，如表1所示2018年6月的收费站出口部分数据，根据陕西省收费公路计重收费技术要求（数据字典）进行查询。主要包括如下数据：StartTime 表示开机时间；SerialNum 表示序列号；CardNetwork 表示卡网络标号；ExitTime表示出口日期及时间；ExitDate表示统计日期等。通过数据字典知ExitTime 是操作发生时的自然时间（只增加），其数据是可用数据，每条数据代表一辆车，然后通过Oracel数据库按时间排序并导出ExitTime数据，保存为.CSV文件。

根据上步提取到数据，通过降采样的方式，每隔15 min进行一次车流量统计。因为预测的准确度取决于数据粒度，更细的粒度可以提高模型的性能[18]。每隔15 min同时也符合短时交通流要求。

2.2 数据预处理

本文采用2018年6月份的出口数据进行实验，通过上步的降采样已经统计出了每隔15 min 的短时车流量。通过查看文件，最后有一两个7 月份的异常数据，这时进行了删除操作。

表1 2018年6月收费站出口部分数据

如若遇到缺失值，这里有多种插补方法，如均值/中位数/众数插补、使用固定值插补、最近邻插补、回归插补以及插值法等。本文若遇缺失值使用的是拉格朗日插值法。该方法根据缺失值前后的数据值拟合一条多项式曲线来插值，该方法结果具有一般性。其原理大致如下：

对于一个平面上的已知n个点可以找到一个n-1次多项式，使该多项式曲线过这n个点。假设该多项式如下形式：

其中，ai为系数，i∈[0,n-1],n为正整数，x为横坐标值，y为多项式曲线对应坐标点函数值。将n个点的坐标(x1,y1),(x2,y2)…(xn,yn)代入式（1）解出拉格朗日插值多项式为：

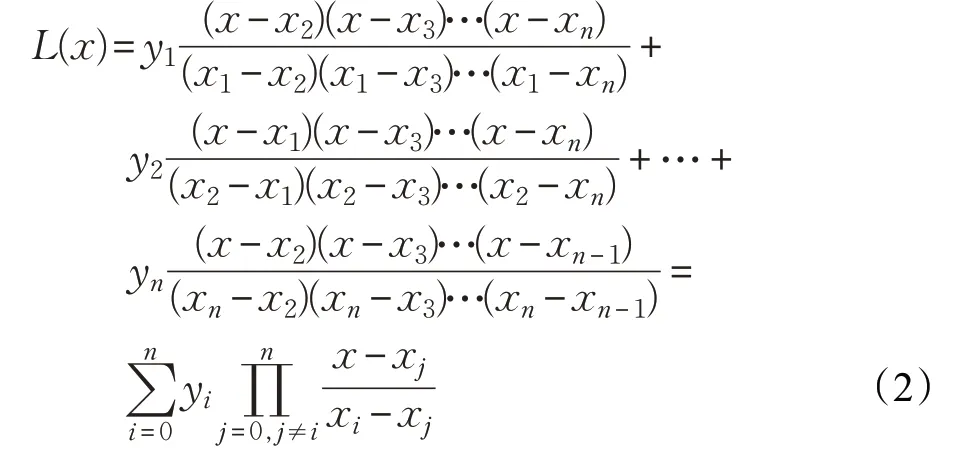
其中，L(x) 为多项式，(xi,yi) 为相应的坐标点，i∈[1,n],n为正整数。

通过上述的处理，如图1 所示，选取了2018 年6 月19 号、2018 年 3 月 9 号、2017 年 10 月 2 号和 2018 年 6 月16号的数据，绘出了当日的车流量随时间的变化图，横坐标代表时间，纵坐标代表当前时刻的车流量信息。通过对车流量信息图分析得，图1 中（a）、（b）在正常情况下，早上8：00 左右和18：00 左右有两个高峰，这大部分是由于上班早高峰和下班晚高峰引起的。而在8：00—18：00处于一定的稳定状态。这些现象符合车流量早晚高峰现象，通过对车流量的分析和预测，对交通部门和人们出行具有实际的指导意义。但是对于节假日和天气影响下，与正常情况下的流量图相比较，早晚高峰不明显且在白天波动较大。如图1（c）、（d）所示，（c）是在法定节假日中的交通流量图，（d）是在雨天时候的交通流量图。通过（c）、（d）对比也可发现，法定节假日的车流量最高值明显大于雨天的车流量最高值，因为雨天的不安全因素较多，所以驾驶车辆出行减少，而在节假日大多数人会选择自驾游，因此驾驶车辆数量会增加。这些现象也符合平时人们的日常生活。

2.3 多因素处理的Classify方法

通过网络查询当地气候类型，西安属于温带半湿润大陆性季风气候，四季分明，气候温和，雨量适中，雨季大部分集中于春夏两季。因此本文选取的是六月份的数据，且通过上面描述，已经处理成为以15 min 为间隔的短时交通流数据。

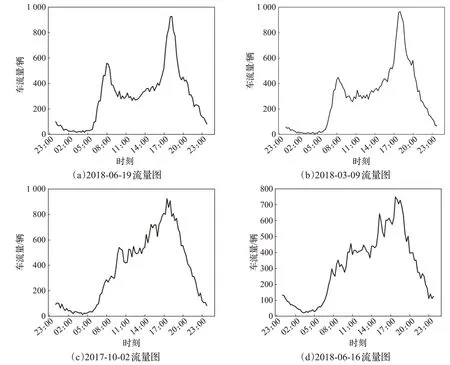
图1 车流量信息图

2.3.1 天气因素处理

通过天气预报查询天气记录，对短时交通流数据根据天气记录进行筛选，根据式（3）得到不同的天气影响强度因子，将天气影响强度因子大于天气阈值的时间段划为异常天气时间段。

其中，Vi表示不同天气情况下的车流量，T表示当月的总车流量，i代表不同天气，例如晴天、阴天、小雨、中雨、大雨、雾天等，ci表示不同天气的影响系数，θi代表天气影响强度因子，所述的天气阈值为晴天时θi的取值。

通过分析，大雨天气车流量明显减少，此时c（ii代表大雨天）的取值与正常天气情况下的取值相比较小，故ci越小，说明天气影响程度越大。再由ci的导数求得θi，即天气影响强度因子，θi越大，说明当日天气情况对当日的车流量影响越大。例如，以2018年6月份收费站出口的部分数据为例，统计6 月份总车流量T为855 418辆，并通过上式计算得到不同天气影响强度值，如表2所示。

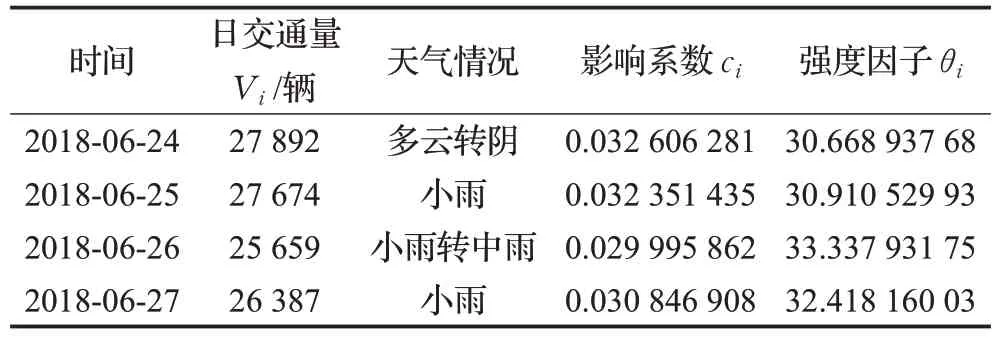
表2 不同天气影响强度表

通过表2，知道每天的日交通量Vi、天气情况以及当月总车流量T=855 418 辆，于是分别求出影响系数ci,分别为0.032 606 281、0.032 351 435、0.029 995 862、0.030 846 908，考虑到天气情况，分析得出天气越不好（如小雨转中雨），影响系数ci就越小。最后求出强度因子θi，其值分别为30.668 937 68、30.910 529 93、33.337 931 75、32.418 160 03，此时可以分析得出影响系数ci越小，强度因子θi越大。最终按照强度因子的大小，将天气划分为不同影响等级。如小雨天气下强度因子为30.910 529 93，可将其影响等级划分为1；小雨转中雨天气下强度因子为33.337 931 75，可将其影响等级划分为2。

故通过θi的取值大小将i天气（i可取晴天、阴天、雨天、雾天等）对短时交通车流量的影响划分为4个等级：

0代表无影响；

1代表稍有影响；

2代表有影响；

3代表有较大影响。

保证车流量正常天气状况下的纯洁度，对有影响的天气下的数据进行筛选操作，并分类存储，如表3所示。

表3 天气分类存储数据表

若出现除此之外的恶劣天气，包括中雪、大雪、沙尘暴、暴雨、台风等也可将其考虑进去，但对于当地来说，这些天气极为罕见。

2.3.2 节假日因素处理

查询节假日记录，对得到的短时交通流数据根据节假日记录进行筛选，根据式（4）得到节假日影响系数，将节假日影响系数大于节假日阈值的时间段划为节假日时间段。

其中，Ej表示不同节假日情况下的车流量，βj表示节假日影响系数，j表示不同节假日，所述节假日阈值为非节假日时βj的取值。

通过分析，比如十一黄金周车流量在十月明显增加，此时Ej（此时j代表十一假期）的取值与非节假日取值相比较大，而当月总的车流量T一定，故Ej的取值越大，则输出βj越大，说明此时节假日对车流量的影响较大。根据法定节假日的放假天数及节日所在的季节及βj，可将影响等级划分为3个等级：

等级1代表稍有影响；

等级2代表有影响；

等级3代表有较大影响。

为了使对车流量的预测更为准确，如若数据中包含了节假日的数据，就对其进行筛选操作，如表4所示。

表4 节假日分类存储数据表

3 Long Short-term Memory神经网络

循环神经网络常用来处理序列数据。循环神经网络因为有梯度消失这一问题，只有短期记忆。为了避免这一问题，循环神经网络产生了一个变体——长短期记忆网络（LSTM）。LSTM在循环神经网络的基础上增加了一些门结构，通过门的控制将短期记忆与长期记忆联合起来，一定程度上解决了普通的循环神经网络梯度消失的问题。LSTM由Hochreiter & Schmidhuber于1997年提出，并在近期被Alex Graves 进行了改良和推广。在很多问题上，LSTM 都取得了巨大的成功，并得到了广泛的使用。

LSTM通过门结构来控制和保护细胞状态C，特点是使用了3个由乘法运算和sigmoid神经网络层构成的门单元。第一步是通过遗忘门来实现的，可以理解为“记住之前内容的多少”，这一步使用了sigmoid 函数和乘法操作来实现，输出为ft，然后输入门单元决定需要更新的内容，输出为it，最后由输出门单元在之前的基础上进行滤出，输出为ot。各个门单元的更新如式（5）～式（7）所示：

其中，Wf、bf、Wi、W0、b0分别是各门单元的权值和偏移量，δ表示激活函数sigmoid。除去3 个门单元外，细胞状态ct在不断随着时间流动，根据式（8）得到，根据式（9）用和ct-1更新ct。这里的Wc、bc分表代表权值和偏移量，使用tanh作为激活函数。这一层神经网络的输出值ht由输出门单元与使用tanh激活后的细胞状态控制，如式（10）所示。

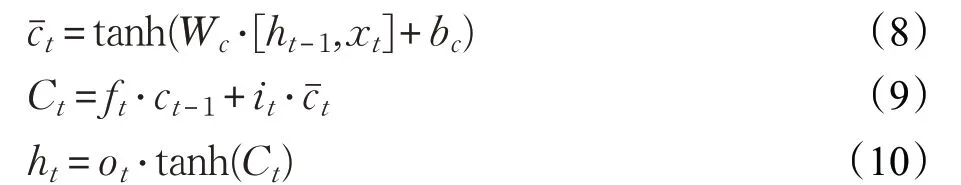
上述表达式中所使用的sigmoid激活函数如式（11）所示，能够将实数域映射到[0，1]的范围内。

综上所述，LSTM 利用门单元，增强了循环神经网络的记忆力，通过训练数据不断更新各个门单元的权值和偏移量，最终确定合适的值。在预测阶段，利用训练好的模型对输入数据进行运算，得到最终的预测结果。

4 实验结果分析

本文依据陕西省高速公路收费站现场调查和历史真实数据，通过Oracle 数据库导出交通流的重要信息。本文考虑到天气因素，取2018 年6 月份的数据，以降采样的方式每15 min统计一次，通过本文上面所述的数据预处理、多因素处理的Classify 方法对数据进行处理。在该网络中模型参数如下：batch为512，epochs为1 000，validation_split为0.05，Dropout为0.2。

观察数据，在6月16号到18号，连续三天都是小雨转阴。这时以6 月1 号到18 号的数据为训练集，以6 月19号为测试集去预测6月19号的车流量情况，通过以往天气数据得知6月19号也是以多云为主，天气状况与前三天不同，测试效果如图2（b）所示，其中图2（a）所示是训练过程的损失可视化，其过程是波动下降，大约在400 epochs 左右趋于稳定。再将6 月16 号到18 号的数据删除，排除连续三天的小雨转阴的情况，再将排除天气之后的数据作为训练集，以6 月19 号的数据为测试集，预测19 号的交通流量情况，预测效果如图3（b）所示，其中图3（a）是在排除天气因素后训练数据的损失可视化，其过程也是波动下降，在0～200 epochs时下降较快。

图2 未排除天气因素时预测结果图

如图4 所示，（a）是未排除天气因素时训练过程中的mean_absolute_percentage_error变化值；而（b）是排除天气因素时训练过程中的mean_absolute_percentage_error变化值。通过肉眼很难辨别出两者的好坏，通过运行程序，得出（a）在1 000 epochs时最后的输出值为25 965.045 9；（b）在训练到1 000 epochs 时的输出值为24 871.074 2；通过对mean_absolute_percentage_error 值比较，得出在排除天气因素后训练数据时效果会较好。

通过结果对比来看，图2（b）的拟合度不如图3（b）的效果好。表5是图2和图3的多个模型评价指标数据。

由于MAE、MSE、RMSE 使用的是平均误差，而平均误差对异常点较敏感，如果回归器拟合的某个回归值与真实值存在较大差异，将会导致平均误差值较大，对最终的评估值产生较大影响，即平均值不具有鲁棒性。通过分析比较以上的评估指标，选择了MAPE、Explained_variance_score、R2作为最终的评估指标。通过对比分析，如果不进行多因素处理的Classify方法，此时的MAPE为 16.343 869%，Explained_variance_score 为 0.968 118，R2为0.968 096。而通过多因素处理的Classify 方法之后，MAPE降低了近5个百分点，Explained_variance_score提高了近1个百分点，同时R2值也提高了。即由实验可得，通过多因素处理的Classify方法之后，预测精度有明显的提高，能够更为准确地反映道路交通流的变化特征。

图3 排除天气因素时预测结果图

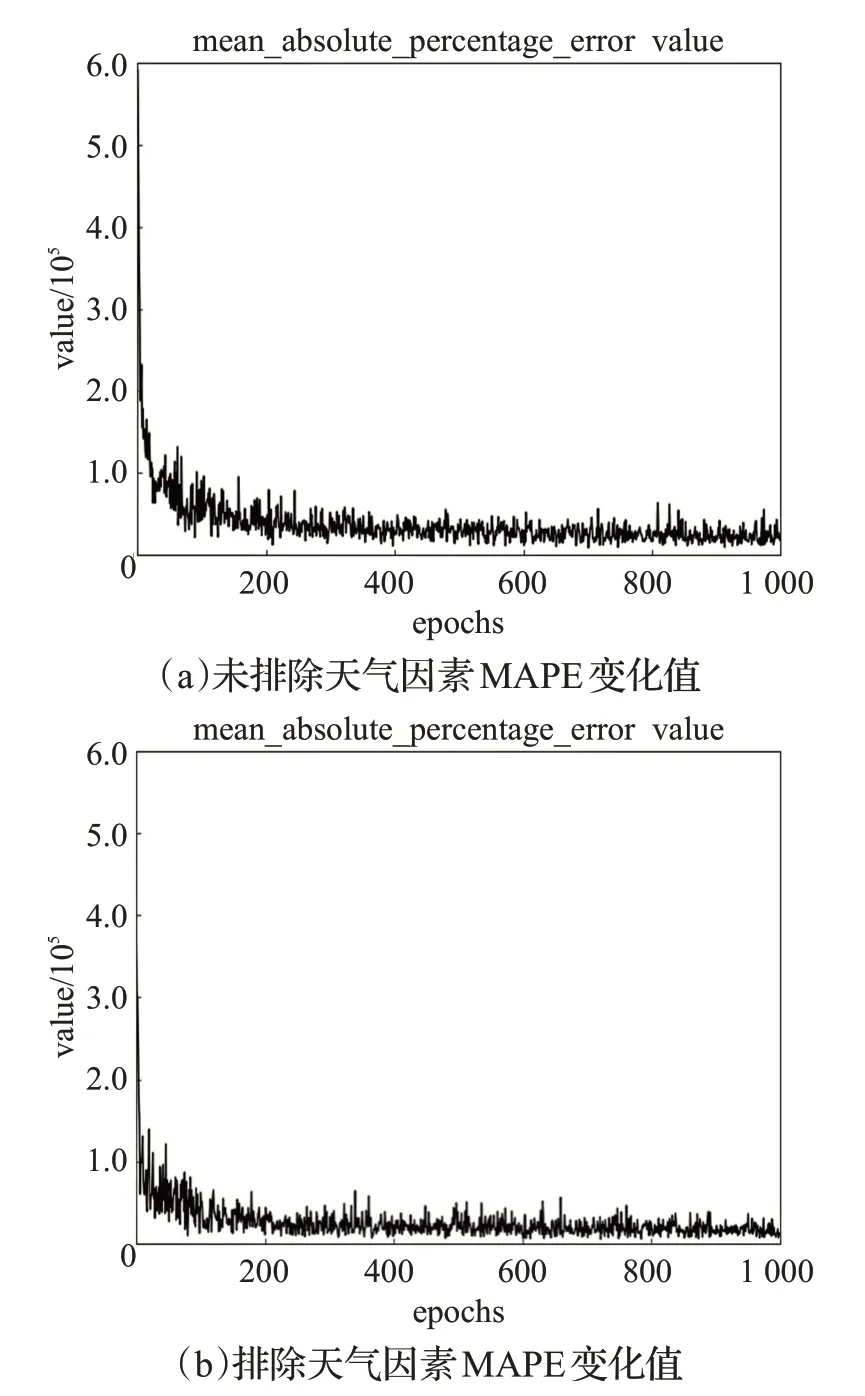
图4 训练过程中MAPE变化值

表5 不同评价指标数据

5 结束语

本文提出了一种结合深度学习的短时车流量预测优化方法，对车流量的不同因素进行了分析，如天气、节假日等，通过多因素Classify方法，对不同因素下的数据进行了分类，降低了多种因素对车流量预测的强度，更进一步保证了数据因素的单一性和纯洁性。同时使用了深度学习的Long Short-Term Memory 神经网络，在一定程度上解决了时间序列的记忆问题。LSTM 通过门的控制将短期记忆与长期记忆联合起来，解决了普通的循环神经网络梯度消失的问题。经过多次实验和测试，与传统的车流量预测方法相比，通过多因素Classify方法对多种因素进行分析和处理，能够很好地提高对不同情况下车流量预测的精度，使得预测更为准确，能够更好地反映道路交通的变化特征，对交通管理部门和人们出行具有实际的指导意义。