综合曲率约束的在线网格模型分割方法研究

赵云成，王 琳 ，盛步云，赵飞宇

1.武汉理工大学 机电工程学院，武汉 430070

2.湖北省数字制造重点实验室，武汉 430070

1 引言

近年来，随着Web 技术的发展，计算机辅助设计与数字几何处理均有向Web环境发展的趋势。“三维扫描+在线重构”的逆向建模方式，凭借低门槛和便捷性，逐渐成为在线三维建模软件的主要建模方式。将三维扫描仪扫描重构的三角网格模型转化为可参数化设计的实体模型，需要对无法编辑的三角网格模型进行分割处理，并分别将每块分割区域重构为可参数化驱动的基本实体特征[1]。从完整的三角网格模型中划分和识别特征区域的研究，有助于实现基于三维扫描的逆向实体建模，提升产品逆向设计效率，对大众参与的计算机辅助设计领域发展具有重要意义[2]。在Web环境下实现网格分割，不仅要求保证三角网格模型分割的准确性，而且须确保分割算法具备较低的计算复杂度以适应在线高并发环境，从而满足Web 环境对数字几何处理高效性、实时性的要求。

国内外学者对应用于不同几何处理领域的三维模型分割做了大量的研究，并提出了一系列网格模型分割方法。根据分割方式的不同，模型分割大致可分为三类：聚类分析法[3-4]、区域增长法[5]和边界检测法[6]。基于聚类的分割方法主要通过聚类算法，对网格模型中具有相同几何信号的点和面片进行迭代聚类，常用于模型块分割。文献[7]将三角网格模型向谱空间映射，进而通过K-means聚类实现分割。文献[8]基于最小主曲率以及特征向量对扫描后自由曲面模型进行块分割，并用于牙齿扫描模型的语义分割。文献[9]在GPU上基于高斯曲率和平均曲率对面片进行顶点聚类，实现了GPU 环境下网格模型的分割。这类算法基于全局信号的迭代聚类，分割效率较低，且分割结果难以预测，不满足Web环境下几何处理应具备较低计算复杂度的要求。基于区域生长的模型分割方法主要将局部几何信号作为分割驱动信号，通过选取种子点和相应的生长规则将满足条件点和面片合并在同一区域中。文献[10]通过计算测地距离选取种子点，基于凹凸信号合并相似区域，实现对三角网格模型的面分割。这类算法虽然具有较高的分割效率，但是区域增长易受到驱动信号的影响，且容易存在过分割等现象。另一类算法则是基于边界的方法，通过在模型上构造符合分割特点的分割线，并以分割线为边界，将模型分割为多个独立的特征面。文献[11]提出了基于分割边界学习的分割线提取算法，该方法通过大量的网格模型人工分割结果来训练分类器，进而获取网格模型的分割边界。该类方法虽然能够获得较好的分割结果，但是在前期训练需要繁琐的数据采集，因而算法总体效率不高，不适用于Web环境下高效分割网格模型。

根据以上分析，本文提出一种基于凹特征区域分割线提取的在线三角网格模型分割方法。首先采用微分几何方法对模型各顶点的离散曲率进行计算，然后根据模型的曲率特性设定阈值来计算判断模型的凹特征区域，在此凹特征区域提取出分割线并进行闭合和光顺处理，最后基于分割线将模型分割成不同的区域。实验表明，本文方法能够实现Web环境下高效快速准确的分割三维模型，且分割的结果具有可预测性，适用于工程实践，便于后期参数化重建研究。

2 三角网格模型分割流程

传统的基于曲率的网格分割方法往往依据单个曲率特征来实现网格模型的分割[12]。或基于曲率信号迭代聚类，或根据曲率结合特征信号进行轮廓特征提取。同样是基于曲率分割，不同的方法运用不同的曲率特征，文献[13]算法利用主曲率，文献[14]算法利用高斯曲率与平均曲率，有的方法基于最小值准则分割模型，有的则基于平坦性原则利用二次曲面（如可展曲面）控制分割过程，还有的算法利用语义或人的视觉原理指导网格分割。

本文将平坦性规则与最小值准则结合起来，在满足Web环境下计算复杂度较低的要求的情况下，综合高斯曲率、平均曲率以及最小主曲率，通过二次提取特征点方法来提取网格模型特征区域，避免了多次全局信号计算。进而在凹特征区域中获取优化分割边界线，实现Web环境下网格模型的高效准确分割。

如图1 所示，本文方法的分割大致流程为：首先根据离散曲率公式计算网格模型各顶点的离散曲率特性；其次根据平坦性规则，利用高斯曲率与平均曲率提取模型中凹区域，在凹区域中利用最小曲率阈值提取凹特征区域，并由此特征区域提取和优化形成闭合分割线，实现对网格模型的块分割。

2.1 网格模型离散曲率估计

在逆向工程中，包含凹形状的特征区域是基于特征建模等操作的重要考虑部分，而高斯曲率KG和平均曲率KH是判断网格模型顶点凸凹特性的重要指标。对PSB中人工分割结果分析可知，分割边界的顶点一般在负的最小主曲率处。因此在通过高斯曲率KG和平均曲率KH确定模型凹区域之后，定义最小曲率阈值KT。将低于最小曲率阈值KT的边界点视为特征点，提取模型凹特征点集，作为网格划分边界线的基础。

目前离散曲率估计方法有很多。其中文献[15]提出的Voronoi图方法比较灵活和准确地估算了任意三角网格模型顶点的曲率。考虑Web 环境下计算低复杂度的要求，在满足曲率估算尽量准确的情况下，本文采用顶点的一环邻域进行计算，得到三角网格模型顶点vi的平均曲率计算公式：

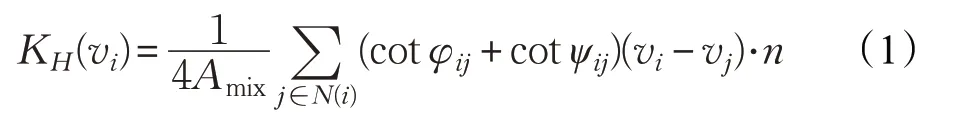
式中，φk、ψk分别为边的对角，如图2（a）所示。Amix表示顶点vi邻域内三角面片对应的区域面积，其公式为：

图1 网格模型分割方法总体流程图

其中，Svi表示顶点vi邻域Voronoi图划分区域（灰色部分）的面积[15]，由于vi邻域三角形夹角θk大小不同，面积取值规则不同，如图2（b）、（c），定义三角面片T的三个顶点vi、vj、vj+1，定义边的夹角为φ，i边的夹角为ψ。不同角度取值规则如下：i

根据微分几何中GaussBonnet 定理[16]，可以通过下列公式得到高斯曲率：

图2 网格顶点离散曲率估计示意图

式中，KG(vi)为顶点vi的高斯曲率，θk表示顶点vi与其邻域第k个三角面片的夹角，Amix表示顶点vi邻域内三角面片对应的区域面积。

顶点vi处的主曲率可由离散曲率和平均曲率计算得到：

式中，K1(vi)和K2(vi)分别为最大、最小主曲率。

2.2 三维模型凹特征区域提取

顶点的高斯曲率和平均曲率反映了顶点的凹凸性，由于模型可能存在噪点，仅仅根据离散顶点本身的曲率特性无法判断区域的凹凸性。本文通过微分几何特性综合各顶点邻域的高斯曲率与平均曲率来判断模型凹区域，并根据归一化最小主曲率阈值在优化后的凹区域中提取出模型的凹特征区域点集。首先根据顶点邻域的高斯曲率和平均曲率筛选出凹点集区域，在凹区域划分中，噪点存在可能导致出现细碎划分，影响凹特征点集提取。噪点存在处往往区域较小且连通性较差，因而本文根据邻域面积和曲率分布状况优化和删除顶点数量过少凹点集，在此凹区域中基于最小主曲率筛选出凹特征点集。不同模型的最小主曲率范围不同，考虑分割边界尽量在最小主曲率处，本文采用提取凹区域中顶点主曲率较小点集作为凹特征点集。具体步骤如下：

步骤1 计算网格模型各点离散曲率。计算网格模型中各顶点vi的高斯曲率KG和平均曲率KH。

步骤2 凹点集初提取。遍历每个顶点vi，获取顶点vi以及顶点vi的一阶邻域各点的离散曲率特性。判断该点一环邻域中所有点的高斯曲率KG和平均曲率KH是否满足KG＜0&&KH＜0，将满足条件的点加入凹点集中。

步骤3 凹点集区域扩展。计算步骤2 中获得每个顶点vi一阶邻域顶点在凹点集区域中所形成的凹三角形面积Sconcave与顶点vi一邻域所有顶点形成面积Sall的比值M，若M＞threshold1，将顶点vi邻接点加入凹点集区域。

步骤4 凹点集区域删除。计算步骤3 得到凹点集区域中所有连通分支顶点数量N以及平均高斯曲率KH,将满足N＜threshold2&&KH＞0 的连通分支删除，得到最终的凹点集区域。

步骤5 凹特征区域提取。计算凹区域点集中点的最小主曲率K2，通过设定归一化阈值KT，将凹点集中主曲率较小部分点加入凹特征区域。

如图3 所示，在凹特征区域的提取过程中，凹点集区域扩展中面积比值M过小易造成点集扩展过多，对区域优化效果不好，在凹点集区域删除过程中对扩展后顶点数量较少以及高斯曲率较大的凸区域(KH＞0)进行删除。本文结合实验测试结果，最终确定threshold1取值0.8，threshold2取值6，凹区域特征提取效果较优。由于初提取的区域最小主曲率分布往往不太一致，因而本文采用归一化阈值。在设定KT过程中，本文通过对PSB 模型人工分割数据集中众多相同或相似轮廓进行阈值估计，并结合实验结果最终设定归一化阈值KT为0.5，取得较好的区域提取结果。

2.3 分割线获取和优化方法

2.3.1 初始分割线生成

如图3Teddy 模型凹特征区域提取所示，特征点在网格边界附近呈区域分布，不能作为最终的分割边界，为了获取精确的分割线，需要在特征点集中区域提取出分割线来。在满足Web环境低计算复杂度要求条件下，考虑分割线生成尽可能平滑。对于三维空间的凹特征点集，本文提出一种基于球面半径搜索方法来连接特征点生成初始分割线，在确定初始种子点后，以最大特征边长为半径，搜索邻域内与连接边夹角最大的特征点，形成分割线。具体步骤如下：

步骤1 移除G中离群点。计算每个特征点vi到其余特征点的平均欧氏距离假定平均欧式距离服从高斯分布，求得的均值μ与方差σ。将分布在±3σ之外的特征点视为离群点并移除。如图4（a）、（b）所示，红色离群点被移除。

步骤2 设定初始种子点。选定凹特征点集中两邻边夹角大于135°的点作为初始种子点，加入到组点序列中。如图4（c）所示，选定vp作为特征线起点。

步骤3 确定搜索半径R。遍历凹特征区域中所有的边，找到长度最大的边，将最大长度记为Rmax，以vp为球心，以Rmax为半径确定搜索区域。

步骤4 寻找分割线的连续点。获取搜索区域的特征点集合，计算球心点vp与特征点组成线和球心点与前一点组成边的夹角ω，选取夹角最大的点加入到组点序列。如图4（c）所示，夹角最大，选取v b加入组点序列。

步骤5 获取所有特征点。球心点移动到下一特征点，重复步骤4，直到遍历完所有特征点。

步骤6 生成初始分割线。将搜索得到的组点序列进行连接得到初步的分割线。如图4（d）所示。

图4 初始分割线生成方法图

2.3.2 分割线闭合及光顺

在初始分割线生成之后，往往存在模型分割线不闭合特征，多为一侧具有明显凹特征，另一侧较为平坦或凸起，大致为L 形状。如图3 中圈出区域所示Teddy 模型腿部与后臀部连接处较为平整，而躯干与腿部处存在凹特征区域，导致生成的分割线无法确保分割区域的封闭性。本文提出基于射线的边界线闭合方法，通过捕获射线与面片的交点获得分割线形状，通过修正交点获取闭合分割线。

步骤1 构造射线。为确保射线由模型内部发出，选择构成边界线的质心点vg为射线起点，通过连接vg与端点va、vb构建单位向量es、ee，求得两向量夹角Φ=arccos(es·ee)，之后构造n条单位夹角为φ的射线 (0＜φ ＜Φ)，分别与模型面片交于{P1,P2,…,Pn}。

步骤2 计算交点Pi。通过建立空间Octree搜索结构，并通过矢量分解判断射线l与三角面片是否相交。构造射线参数方程，计算射线与三角面片交点Pi。

步骤3 修正交点。鉴于Pi位于三角面片T的内部，为避免网格细分而增加计算复杂度，须对Pi进行修正。如图5（b）所示，即计算Pi与T三个顶点vi、vj、vk的欧氏距离，选取距离最小的顶点作为修正后的交点vc，表示为：

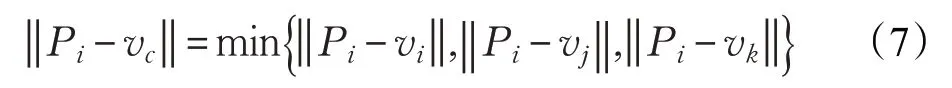
步骤4 边界闭合。运用Dijsktra最短路径算法[17]求得从va到vb并经过所有修正后交点的最短路径，形成闭合边界线Lb。

步骤5 分割线光顺。采用主动轮廓模型（Snakes）[18]，定义边界线上顶点的内部能量Eint与外部能量Eext，借助贪心算法[19]，使曲线上的顶点迭代地向局部范围中能量最小位置偏移，获得光顺分割线。

以图5为例，通过连接vg与v1、v7确定夹角，发出7条射线分别与不同三角面片交于Pa、Pb、Pc、Pd、Pe、Pf、Pg。计算出交点坐标，Pa、Pb、Pc、Pd、Pf、Pe、Pg经过修正得到va、vb、vc、ve、vf、vg、vh。之后运用Dijsktra 最短路径算法形成闭合线如图5（c），光顺处理后得到分割线如图5（d）。

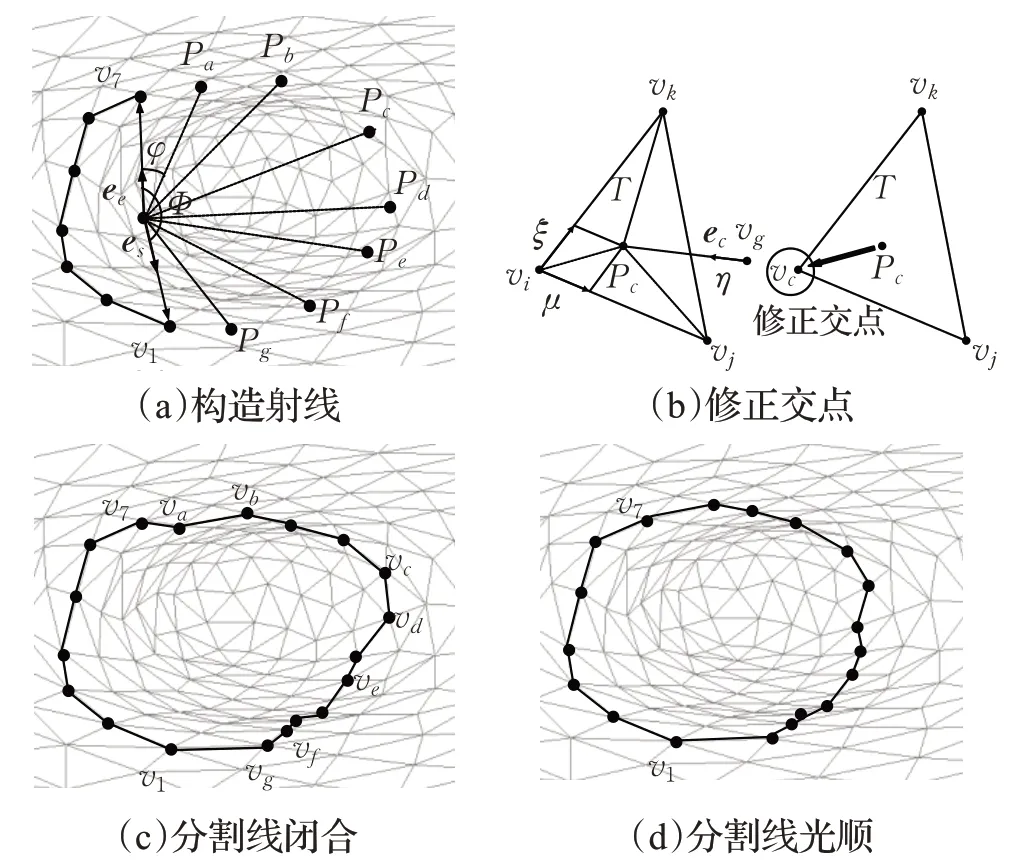
图5 边界线闭合及光顺图

如图6所示，最终得到Teddy模型的分割效果。

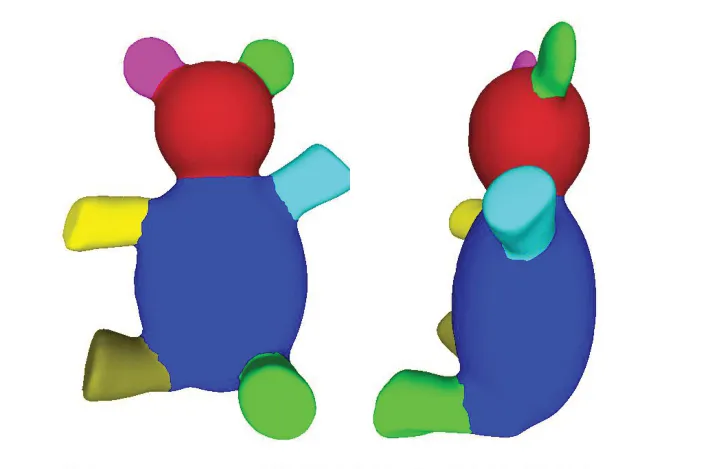
图6 Teddy模型最终分割效果图

3 实验与结果分析

为了验证算法的有效性，本文依托开源数字几何处理软件MeshLabJS，通过开发网格分割Filter插件实现，并部署于Apache 服务器，运用WebGL 的几何处理及图形渲染功能，实现完全在浏览器中的在线网格分割与网格渲染。在软、硬件方面，采用Windows 7 Ultimate x64操作系统以及WebStorm 2016.3.1开发环境，服务器PC采用Intel Xeon-E5 2620V4 2.1 GHz CPU 与32 GB RAM，客户端PC采用Intel®i5-7200U 2.5 GHz CPU与8 GB RAM。

目前，评价三维模型分割的优劣主要是以下几方面：

（1）视觉效果

视觉效果主要是指模型在分割之后，基于人类视觉效果最小值准则，能否将模型分割成具有意义的各个分块，分割结果是否存在过分割。

（2）分割一致性

目前普林斯顿大学提供了一套完整的模型分割评判标准[20]。其中兰德指数（Rand Index）衡量各类算法与人工分割数据的一致性。本文采用评价指标兰德指数，对普林斯顿数据集进行测试，将本文方法与文献[21]中提供的9种算法进行比较。

（3）算法的运行速度

一个良好的网格模型分割算法除了需要在模型分割的视觉效果和结果精确度两方面找到最佳平衡外，还需要有较高的处理速度。本文采用相同模型分割处理消耗时间，将本文方法与兰德指数平均值较低的3种算法进行时效性对比。

图7 展示了本文算法在PSB 数据集中部分具有代表性的三维模型分割效果。图8 展示了本文算法在COSEG形状数据集中部分具有代表性三维模型的分割效果，将不同分割区域中的三角面片标记为不同颜色。从分割视觉效果上看，绝大多数三维分割的视觉效果符合人的认知要求。

图7 本文方法对普林斯顿数据集部分模型分割效果图

图8 本文方法对COSEG数据集部分模型分割效果图

表1 Rand Index评价表

在分割一致性上，分别采用本文算法与文献[20]中提供的9 种算法进行比较。利用兰德指数作为评价指标，对普林斯顿数据集中19种模型进行测试。表1展示了本文选择19种模型在不同评估算法下的Rand Index评价结果。兰德指数越小说明在当前分割下效果越好。从表1中可以看出，对于具有明显分支结构的模型，如Airplane、Chair、Table、Mech、Bearing 等模型，本文算法具有较优的分割效果，分割兰德指数优于大多数算法。

然而在对Human、Glass、Armadillo 等模型分割时，本文算法虽然能分割出模型大致语义，但是由于模型存在太多模糊细节特征，因而分割效果不够理想。从图9平均兰德指数图可以看出，本文方法在分割一致性上优于大部分算法，但是不如深度学习和WCSeg[22]的分割方法。其中深度学习方法的分割一致性最高，本文在兰德指数平均值上接近WCSeg方法。

图9 测试模型Rand Index平均值

在算法运行速度方面，表2展示了本文算法与兰德指数较低的3种算法在分割6种模型时的时效性。由表2可以看出，本文算法由于没有费时的迭代聚类过程，也没有复杂度较高的计算，相较于WCSeg 算法在分割效率上要高，另外相较于机器学习方法，不需要考虑数据集采集以及人工训练时间。

表2 算法时效性分析 s

为了综合评价性能较优的4种网格分割算法，采用熵值法，分别从分割时间、分割差异（CD）、汉明距离（HD）、基于缺失率的汉明距离（HD-Rm）、基于误报率的汉明距离（HD-Rf）、兰德指数（RI）、全局一致性误差（GCE）和局部一致性误差（LCE）共8个指标进行综合评价。熵值法充分考虑指标对评价结果的决定性作用，削弱了主观因素对评价结果的影响，有助于获取更为客观、真实的评价结果。将4 种网格分割方法的8 项指标值分别统计于表3。

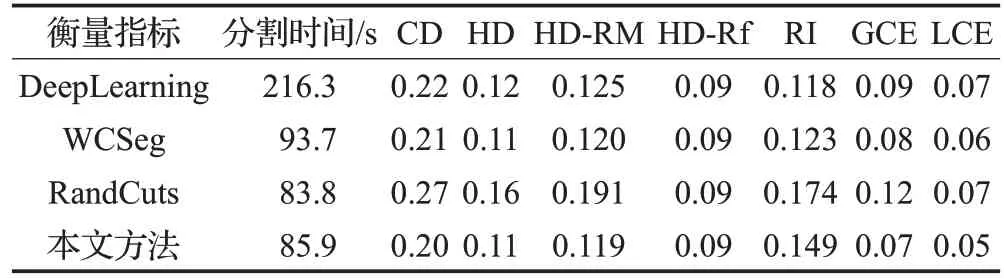
表3 不同网格分割算法指标值

在对所有指标进行负向归一化处理后，考虑到在线网格分割要求算法具备较低的时间复杂度，因此分割时间的主观权值均取0.15，其余指标主观权值取0.10，求得各指标熵权值，并统计于表4。最终，根据相对权重向量与归一化后的指标矩阵，求得6 种方案的综合评分，见表5。由综合评分结果可知，在以网格分割快速性为主要导向的前提下，本文方法在算法执行效率、快速性方面具备明显优势的同时，能够兼顾分割可视化效果与分割快速性，适宜在Web环境下执行。

表4 各指标的熵权值

表5 4种方案综合评分

4 结束语

本文提出了一种面向Web的快速网格分割方法，其目的是为解决Web 环境下网格的在线快速分割。首先综合离散曲率特性提取出模型的凹特征区域，利用特征区域点集提取出模型的闭合分割线，最终实现在具有较好分割效果情况下对网格模型的快速分割，并通过模型数据集对分割结果进行分析，验证了本研究对在Web环境下实现网格的数字几何处理具有一定的意义。

由于本文方法应用于Web 环境下扫描得到网格模型实体建模的区域分割，因而分割高效准确性要求较高，未来研究应侧重于两方面：（1）对网格分割算法进行优化研究；（2）考虑研究基于在线机器学习的网格分割方法。