5G动态异构场景下无线回程优化算法

张 晖，李风乐 ，赵海涛，3，孙雁飞，朱洪波，3

1.南京邮电大学 江苏省无线通信重点实验室，南京 210003

2.南京邮电大学 通信与网络技术国家工程研究中心，南京 210003

3.南京邮电大学 教育部泛在网络健康服务系统工程研究中心，南京 210003

4.苏州大学 江苏省计算机信息处理技术重点实验室，江苏 苏州 215006

1 引言

随着科学技术的飞速发展以及人民生活水平的不断提高，各类移动终端设备和移动互联业务得到广泛使用。预计到2030 年，移动终端数量接近1 000 亿台，移动业务流量增长接近2 万倍[1-2]。现有通信系统将很难满足未来海量终端和海量业务的接入需求，有鉴于此，第五代移动通信系统（5G）[3-4]应运而生。另一方面，随着各类交互式多媒体业务（例如视频会议和在线游戏等）的逐步兴起，时延和时延抖动日益成为最为重要的QoS指标，成为影响用户业务体验的关键所在[5-6]。当前研究主要集中在数据包的时延特性分析，而对于时延抖动的研究相对较少。因而，对于面向5G 环境的时延抖动研究势在必行。

业务时延和时延抖动控制主要是以包为粒度在网络链路层实现，通过网络节点对数据包进行转发调度和队列管理。目前，以包为粒度研究时延抖动性能的成果尚不多见。文献[7-8]对网络时延抖动特性进行了一定探索。文献[9]针对多跳无线Mesh 网络，利用时延均方差近似描述时延抖动，通过求解端到端的时延分布，获得时延抖动。需要注意的是，大多数关于时延抖动研究的文献都是基于单点系统，例如仅研究无线接入网或有线核心网的时延抖动[10-11]。然而，5G网络必定是一个复杂多元的异构网络，回程网络是重要的组成部分，将接入网与回程网统一考虑更能真实地描述未来5G网络。

因此，本文针对存在的问题，面向5G 混合回程场景，提出一种以时延抖动为优化指标的信道资源最优分配算法。考虑信道动态特性，对时延抖动问题进行综合分析，得到时延抖动指标，进而构建各类回程优化模型，最后采用分层算法加以快速求解。

2 网络场景与系统假设

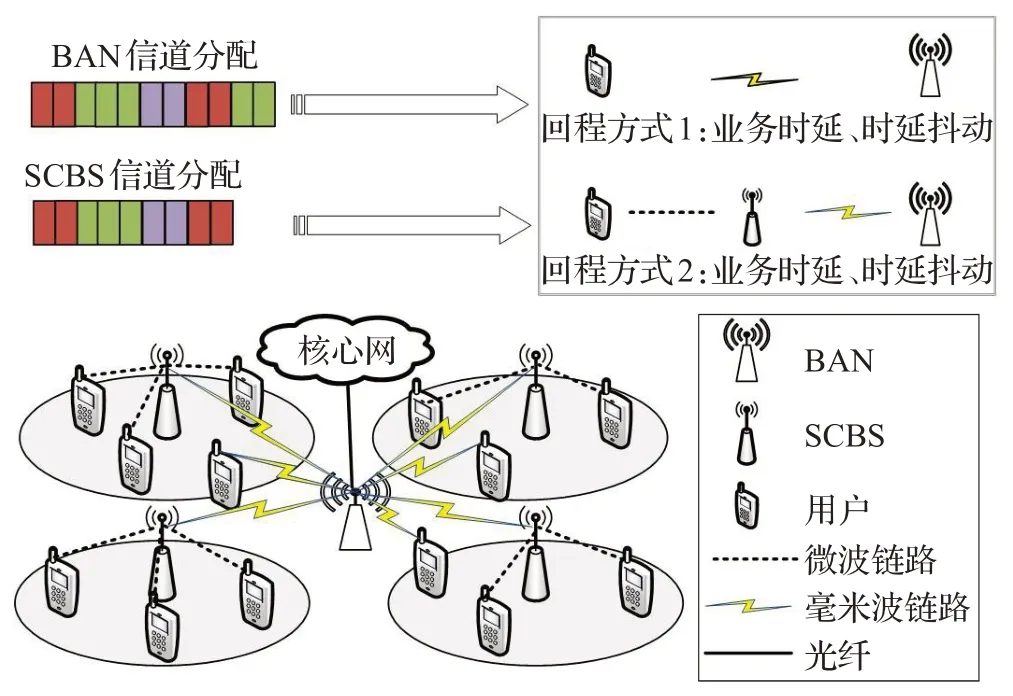
图1 5G两层异构网络场景

如图1 所示，对于两层异构网络场景，上层为一个回程聚合节点（Backhaul Aggregator Node，BAN），下层为被该BAN 所覆盖的多个小基站（Small Cell Base Station，SCBS）。BAN一方面通过专用光纤与核心网进行连接，另一方面通过毫米波[12]与SCBS 或用户进行通信；而SCBS 使用6 GHz[13]以下频段与用户进行通信。这里，BAN 兼有聚合器与基站接入的功能。考虑混合回程场景，有两种回程方式可供选择：第一种，用户可以通过一跳无线链路接入BAN，由BAN 通过有线方式进行回程；第二种，用户可以接入所属SCBS，进而由所属SCBS接入BAN，通过两跳无线链路接入核心网。

定义SCBS 集合SC={SC1,SC2,…,SCl,…,SCL} ，定义小区SCl所覆盖的用户集合为UEl={UEl1,UEl2,…,UEln,…,UElNl} ，其中UEln表示小区SCl的第n个用户，Nl为小区SCl的用户数。假定所有SCBS 共同实现对全网的无缝覆盖，且互不相交，即UEi∩UEj=∅(i≠j)。故用户集合为UE={UE1,UE2,…,UEl,…,UEL},则用户数。

定义接入选择向量为：

其中，aln=1(n≤Nl)表示小区SCl中用户n接入BAN，由BAN 进行回程；aln=0(n≤Nl)则表示小区SCl中用户n接入SCl，由SCl进行回程。

定义SCBS的信道分配矩阵为：

其中，bln,m=1 表示将带宽BWm分配给用户UEln，而bln,m=0 表示未分配。这里，BW={BW1,BW2,…,BWM1}表示SCBS可分配的信道向量，M1为SCBS信道总数。

设M2为BAN 信道总数，定义BAN 的信道个数分配向量为：

其中，cln表示分配给UEln的BAN 信道数量，且cln≥1(∀l,n)。需要注意的，不论用户接入BAN 回程，还是接入SCBS回程，均需为其分配一定数量的BAN带宽。若aln=1，则cln表示分配给UEln→BAN链路的信道数量，用于传输UEln数据包；若aln=0 ，则cln表示UEln→SCl→BAN路径中分配给SCl→BAN链路的信道数量，用于传输UEln数据包。

本文算法基于以下假定：

（1）假设信道是离散的，BAN可分配不同数量信道到任一SCBS 或某个用户，SCBS 亦可分配不同数量信道到某个用户。

（2）针对业务上行传输场景，研究基于数据包粒度的时延抖动指标。

（3）为便于干扰分析，假定BAN 侧和SCBS 侧所有信道带宽相等，且BAN的信道总带宽应大于SCBS的信道总带宽。

（4）假定链路信道容量小于其发送速率，将产生无线丢包；各SCBS 均有无限队列缓存，从而不会因排队（或拥塞）而产生丢包；若链路产生丢包，启动重传机制，重新发送该包。

3 时延抖动指标分析

在无线通信环境下，时延抖动是度量数据包在网络传输中所经历的时延变化的物理量，可定义为数据包传输时延相对于平均时延的波动程度，利用两者方差来描述数据包的时延抖动。故而分析时延抖动问题，首先需要分析时延问题。链路时延包括传播时延和传输时延。其中，传播时延取决于信号传播距离与电磁波传播速度（即光速）。在5G通信场景下，信号传播距离很小，故传播时延非常小，可忽略不记。传输时延则被定义为数据包传输过程中产生的时延。下面分别对业务时延和时延抖动进行系统分析。

3.1 时延分析

在本文场景下，面向UEln的无线链路共计三类：UEln接入BAN的链路、UEln接入SCl的链路和SCl相应接入BAN的链路。假定所有链路信道均服从小尺度Rayleigh 衰落。对于链路、，由于BAN内不重复分配同一信道，故BAN 内无干扰；由于BAN均采用毫米波通信且BAN 之间距离较远，可认为BAN间无相互干扰（近似于On-Off模型）。在以上分析的基础上，记链路的信干噪比为。若≥SINRth，则认为成功传输，由此计算得到链路的误比特率。

而丢包率与信道纠错编码有关。假设所有包的大小均为PL(PL≥3)。本文假定数据包中有3比特错误，则认为丢包，此时数据包需要进行重传，那么丢包率为：

表示从θ个元素选择ϑ个元素的组合个数。由丢包率推导链路的平均传输时延：

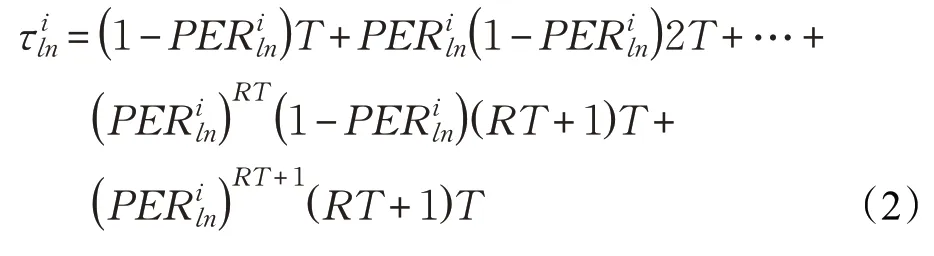
其中，RT为最大重传次数，T表示一次传输时延。

由链路扩展到路径，对于UE→BAN路径的时延分析相对简单，由一跳无线链路直接接入有线核心网，而有线核心网的时延非常小，可忽略不记，故该路径下的无线接入侧的初始时延、业务到达时延均为。对于UE→SC→BAN路径（即UEln经SCl接入BAN的回程路径），Packet1，Packet2，Packet3，…，Packetk到达SCl的时间依次为，则在SCl处无排队拥塞，因此到达BAN 的时间依次为，在SCl存在排队时延，故在SCl的排队时延依次为0 ，各数据包到达BAN的时间依次为综合以上两种情况，从期望平均角度分析UE→SC→BAN路径时延可得，数据包到达时延间隔为初始时延为。

3.2 时延抖动分析

进一步地，可计算链路的时延抖动：

其中，表示链路的平均传输时延，表示丢包率，T表示一次传输时延。式（3）以数学方差形式描述了链路的传输时延相对于平均时延的波动程度[9]。

由链路扩展到路径，对于第一个数据包的传输，因不存在等待时延，各组成链路可视为相互独立的，故路径初始时延抖动为各组成链路时延抖动之和；对于后续数据包的传输，在中间节点存在排队和不排队两种情况，数据包重传机制使得等待时延计算更为复杂，此时各组成链路可视为相互关联的，故路径的时延抖动要小于各组成链路时延抖动之和。为了简单起见，本文采用各组成链路的时延抖动最大值来近似估计整条路径的时延抖动。

对于UE→BAN路径（即UEln直接由 BAN 回程的路径）的时延抖动分析相对简单，由一跳无线链路直接接入有线核心网，假设有线链路无时延抖动，则该路径无线接入侧的初始时延抖动和平均时延抖动均为。对于UE→SC→BAN路径（即UEln经SCl接入BAN 的回程路径），其初始时延抖动为，后续各数据包的平均时延抖动为。

4 优化模型建立

4.1 基本回程模型

在上述时延抖动分析的基础上，优化目标可表示为：

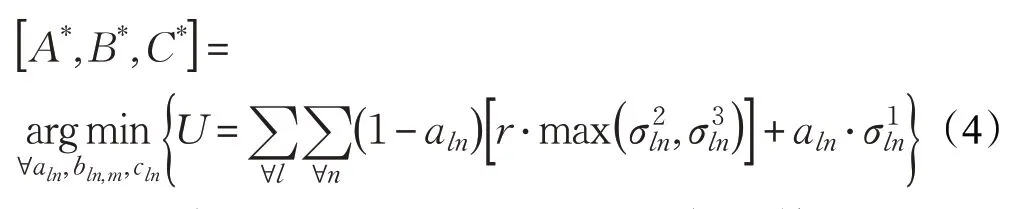
其中，U表示基本回程模型的优化目标函数，可视为所有用户回程路径的平均时延抖动之和，A*、B*、C*分别表示A、B、C的最优解，r≥1 为初始时延抖动补偿因子，以体现初始时延抖动的作用。特别地，当时，表明两类路径的平均时延抖动相同，此时将选择初始时延抖动较小的UE→BAN作为最优路径。

进而，可建立基本优化模型：

式（6）表示UEln要么直接接入BAN回程，则SCBS不予分配信道；或者接入SCBS回程，则SCBS分配若干个带宽。式（7）表示同一小区的同一信道最多分配给某一用户，以避免小区内干扰。式（8）限定了BAN分配的信道数量不能超过其最大值，其中M2为BAN可分配的信道数。式（9）和式（10）限定了aln和bln,m的取值空间。式（11）表示不论用户如何回程，均需为其分配BAN带宽。

4.2 改进模型1

基本模型仅对时延抖动优化而忽略业务时延的优化，故增加用户UEln的回程路径的时延间隔约束：

其中，εln表示最大时延约束，以保障业务的基本时延需求。故构建改进模型1：

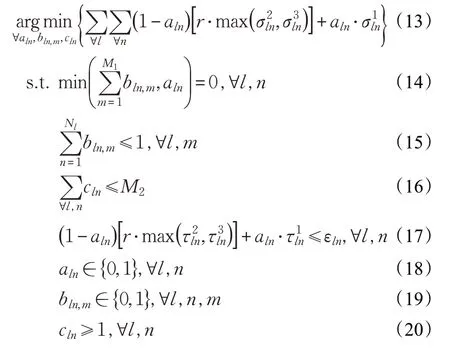
4.3 改进模型2

当用户个数超出网络可用信道量时（即网络超载），上述模型将面临无解的问题，即：

其中，ω为调节因子。若ω较小，则倾向于优化U；若ω较大，则倾向于优化，从而在保证有解前提下尽可能将资源分配给用户。此外，若cln=0，则拒绝用户请求。

5 改进模型求解

改进模型1和改进模型2本质上是整数规划。为快速求解上述模型，根据它们的数学特征，基于分层思想与分支定界思想设计相应求解算法。

5.1 改进模型1求解

在改进模型1 中，解向量A是布尔向量，解矩阵B是布尔矩阵，解向量C是整数向量。据此，将原优化问题分成三层求解。首先，给出初始化过程如下：

第一层，求解向量A。根据式（18）在向量A的每个分量处进行分支，构造多个子问题。每次迭代可求得当前优化问题的一个最优解。其中，ffln表示式（17）左边公式的数值，ff0表示其最小值。算法中f0、{fln} 表示当前可行解的目标函数值。第一层求解，即算法1如下：

第二层，求解矩阵B。在第一层求解的基础上，针对小区中剩余信道进行分配，从而满足式（17）。显然，接入到SCBS 的用户获得更多信道，将相应减小丢包率。第二层求解，即算法2如下：

第三层，求解矩阵C。经过第一、二层求解之后，当前优化问题变为纯整数规划问题。将BAN剩余信道进行分配，每次遍历分配一个剩余信道。第三层求解，即算法3如下：

可以看出，上述求解算法根据解空间特点将原问题分成三个层次的子问题迭代求解，三层子问题可被视为性质不同的整数规划问题，是给定部分变量条件下对另一部分变量的优化问题，采用分支定界方法可得相应问题的最优解，以此迭代求解可逐步收敛到原问题最优解。

5.2 改进模型2求解

在改进模型1 的求解算法基础上，基于改进模型2的数学特征，提出改进模型2的三层求解算法：

第一层，求解矩阵A。将式（25）松弛，设置ω=0。求解过程同于改进模型1的算法1。

第二层，求解矩阵B。求解过程同于改进模型1的算法2。

第三层，求解向量C。在第一、二层求解基础上，需要重新考虑式（25）的约束，进行N-M2次迭代，每次迭代拒绝当前优化结果中时延抖动最大的用户。求解过程如算法4。

6 仿真分析

在500 m×500 m 的区域内，将BAN 设置于中心位置处，4 个SCBS 均匀散布其中，SCBS 的平均通信半径为175 m，以实现对整个区域的无缝覆盖。N个用户均匀分布其间且不具备移动性（拓扑固定），每个用户归属于一个SCBS，所有上行信道均模拟成Rayleigh 衰落信道。此外，重传次数RT的取值将直接影响网络性能：RT越大，传输时延越大，但丢包率却越小；RT越小，传输时延越小，但丢包率却越大。在实际系统中，设RT=5，以取得传输时延和丢包率的良好折中。其他仿真参数如表1所示。

为验证本文提出的改进模型1 求解算法（Improved Model 1 Based Solved Algorithm，IM1SA）和改进模型2求解算法（Improved Model 2 Based Solved Algorithm，IM2SA）的有效性，选择三类无线回程优化算法用于仿真比较。第一类，即面向单一回程场景的无线回程优化算法（Wireless Backhaul Optimization Algorithm for Single Backhaul Scenarios，WBOASBS）[14]，该算法面向单一回程场景（即所有用户均通过SCBS接入BAN进行回程），相应地建立考虑信道动态性的平均时延抖动指标，以此最优化信道分配；第二类，即面向静态信道场景的无线回程优化算法（Wireless Backhaul Optimization Algorithm for Static Channel Scenarios，WBOASCS）[15]，该算法面向混合回程场景（包括两类回程方式），相应地建立不考虑信道动态性的平均时延抖动指标，以此最优化信道分配；第三类，基于初始时延抖动的无线回程优化算法（Wireless Backhaul Optimization Algorithm Based on Initial Delay Jitter，WBOABIDJ），该算法面向混合回程场景（包括两类回程方式），相应地建立考虑信道动态性的初始时延抖动指标，以此最优化信道分配。三类算法的其余部分均类似于本文算法，所有算法均采用Matlab 工具加以代码实现。以时延抖动作为性能指标比较上述算法。这里，时延抖动指将基于不同算法的信道分配结果，分别代入实际网络环境，统计出所有用户的平均时延抖动值。

表1 仿真参数

图2给出了低业务负载情况下（即用户数小于M2），IM1SA 与另外三类算法的时延抖动随用户数的变化比较。可以看出，在不同M1取值下，四类算法的时延抖动均随着用户数N的增加而呈逐步上升趋势；当用户数较小时，网络负载较低，网络性能处于较优水平（即链路丢包率低），此时在不同M1下的同一算法的时延抖动非常接近；当用户数较大时，网络负载较高，网络性能恶化（即链路丢包率高），此时M1越高同一算法的时延抖动越小；在任何情况下，IM1SA 的时延抖动性能始终最优。

图2 四类算法时延抖动比较（低业务负载情况）

图2 仅仅给出低业务负载情况的仿真结果。一旦用户数超出M2，上述四类算法均将面临优化无解的问题，即上述四类算法均无法适用于用户超载的情况。因此，本文提出了IM2SA。图3给出了高业务负载情况下（即用户数大于M2）IM2SA 的时延抖动随用户数的变化结果。可以看出，IM2SA 的时延抖动随着用户数N的增加在一定范围内波动；给定用户数，IM2SA 的时延抖动随着M1的增加呈下降趋势。显然，IM2SA可以有效进行接纳控制并合理分配信道。在用户数快速增加的情况下，基于IM2SA 的时延抖动性能始终维持在一定水平而不至于恶化。

图3 IM2SA时延抖动结果（高业务负载情况）

7 结论

本文针对5G 动态异构场景，提出一种考虑时延抖动的无线回程优化算法。在对动态异构场景下业务时延和时延抖动问题进行系统分析的基础上，建立回程优化指标，构建基本回程模型。进一步地，从时延优化和网络超载两个角度，分别构建改进模型1和改进模型2，并提出分层算法加以快速求解。仿真结果验证了本文算法的有效性。