海底管道抗压溃分析的理论适用性研究

冯春健，陈国龙 ，李 涛 ，卢青针*，崔樱华

（1.中石化石油工程设计有限公司，山东 东营 257026；2.大连理工大学，辽宁 盘锦 124221）

全球经济飞速发展，对能源资源的需求量日益增加，我国新时代的发展规划对我国深水海洋油气田的开发与利用提出了更高的要求[1]。在海洋开发活动中，各种形式的海洋油气管道是海洋油气生产系统的“生命线”，是将油气从地层内部输送至平台、FPSO 或陆上终端，铺设海底管道是最直接、有效的输送方式。随着海洋油气资源勘探开发迈向深水和超深水海域，对管道的抗外压性能提出更高的要求，外压引起的压溃失效是管道设计中需要考虑的重要问题。

海洋管道对应外压荷载的极限承载力称为极限压溃值或临界压溃值，是评价管道抗外压性能的重要指标。对海洋管道抗外压性能的研究可以从理论、有限元分析、实验三个方面在研究。Timoshenko S E 等[2]认为均质管道发生压溃失效时的压力是管道失稳压力的下限值，并将其作为保守的特征值，据此推导出管道失稳压力的经典弹性解析公式。并在经典压溃理论的基础上考虑椭圆度的影响，推导出有一定初始椭圆度的钢管压溃理论。Tamano T[3]以大量试验数据为基础，运用统计方法拟合出管道失稳压力的经验公式。Kyriakides S 等[4]对圆管的压溃进行非弹性分析，与直径和厚度比在10 至10 间的不锈钢和铝管的实验结果进行了比较。结果表明，径厚比大于20 时的理论预测值与实验值吻合较好。Yeh M K 等[5]通过实验和分析研究了长厚壁管在外部压力下的压溃现象，提出了该问题的二维非线性表示方法。Tokimasa K 等[6]利用有限元程序，分析了几何形状、残余应力和材料弹塑性行为对管道抗压强度的影响，得到当内表面上的周向残余应力为拉伸应力时，塑性破坏压力最大的结论，在此基础上，提出计算钢管抗压强度的新公式。张正国[7]讨论了压溃理论在方钢管砼偏压构件中的应用问题, 统计整理出了偏压短柱的强度计算公式和偏压中长柱的稳定计算公式。Kyriakides S 等[8]介绍了在弯曲，压力和拉力共同作用下管道响应和稳定性的组合实验和分析研究结果，提供了正在进行的对在拉伸和弯曲共同作用下的管道响应的初步研究结果。孙田柱[9]等介绍了薄壁钢管拄与圆形钢柱求压溃荷载方法，建立压杆平衡挠曲线和求压溃荷载的方法。Assanelli A P 等[10]研究不同的参数对于管道的外部压力压溃的影响，提出了用于研究钢管压溃的实验和数值技术。API[11]规范给出了管道在一定范围内的屈曲承载力计算公式，已被广泛应用于油气管道的设计，其他因素的影响仍值得进一步研究。余建星等[12]开展全尺寸管道压溃试验，得到结论：管道压溃载荷随着径厚比的增大而显著降低，单个点状凹坑缺陷对于管道压溃载荷影响较小，初始椭圆度缺陷则明显降低了管道的压溃载荷。

目前，均质管道的压溃理论可分为弹性压溃理论、塑性压溃理论与经验公式三种形式。而对于不同径厚比均质管道的抗压溃能力预测，各种理论预测结果的准确性尚缺乏系统的研究。本文面向海底管道的抗压溃能力预测问题，总结了应用较为广泛的三种理论模型，通过数值模型分析了不同理论模型的局限性，给出了各理论模型适用的径厚比范围，并结合实验验证了数值模型的正确性。

1 压溃理论分析模型

1.1 弹性压溃理论模型

假设有一圆环结构，均匀分布的静水压引起屈曲压溃。发生压溃失效时，管壁应力状态仍处于弹性阶段，即弹性压溃，模型如图1 所示。Timoshenko S E 等[2]以此模型为基础建立了中心线为圆弧的细杆挠度曲线微分方程，推导过程中假设径向挠度为小变形，同时细杆切向变形忽略不计。

式中：ω 为细杆径向挠度变形；θ 为环向角度；M为施加在细杆截面上的弯矩；EI为细杆初曲率平面内的弯曲刚度；R为细杆的曲率半径。

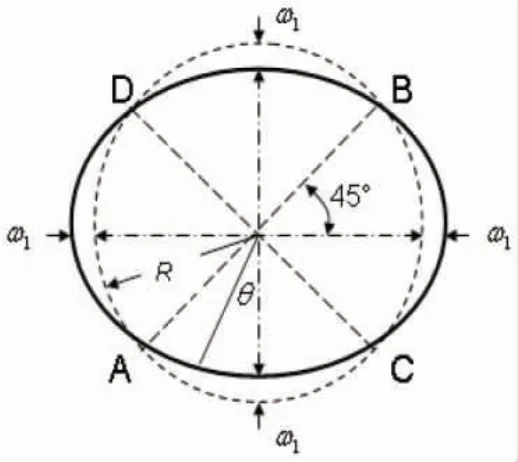
图1 Timoshenkoti 压溃模型

根据该微分方程在压溃模型A、B、C、D 四点处的连续条件，得到方程（1）的解析解，并进一步计算得到平面圆环在均布外压作用下发生弹性失稳时的一阶临界压溃值：

式中：E为弹性模量；I为截面惯性矩

对于圆筒钢管结构，截面为矩形，单位长度的截面惯性矩I可以展开为t3/12，同时考虑平面应变条件，圆筒的临界压溃力公式可进一步写为：

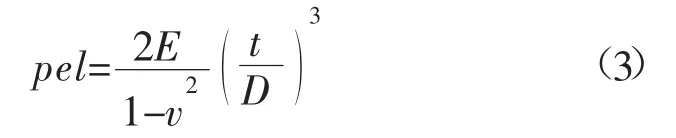
式中：υ 为管道材料的泊松比；t为管道厚度；D为管道直径。

1.2 塑性压溃理论模型

考虑到材料的非线性因素，假设均质管道在在均匀外压作用下，当管壁应力达到材料屈服强度σy时发生压溃失效，即塑性压溃。假定材料为理想弹塑性材料。

式中：D为直径，且D=2R。

在此基础上考虑初始椭圆度的影响，外压引起的管壁应力和由于椭圆度引起的额外弯矩引起的应力之和达到材料屈服极限时发生压溃。

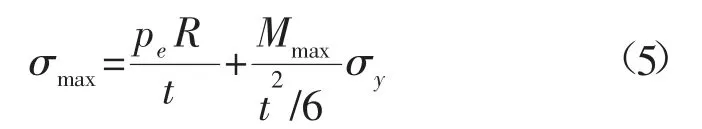
式中：pe为外压；σy为材料屈服强度；R为管道半径；t为管道厚度；M为施加在管道上的弯矩。

继续推导得到考虑椭圆度时的塑性压溃极限值：

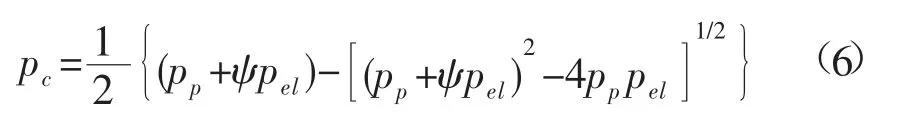
式中：ψ=1+3Δ0(D/t)；

管道初始椭圆度Δ0定义为：

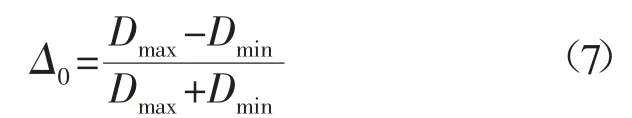
式中：Dmax和Dmin分别为管道的最大和最小直径。

1.3 DNV 规范经验公式

除了上面提到的弹性压溃计算公式和塑性压溃计算公式，API[13]规范中根据大量压溃实验的结果对上述计算公式进行修正校准得到了极限压溃值pr的经验公式：

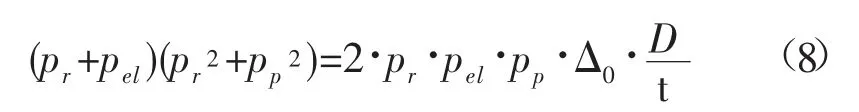
通过求解关于Pr的一元三次方程可以求得极限压溃值。该公式规定适用于椭圆度Δ0≥0.5%且径厚比 15＜D/T＜45 的情况。

2 有限元分析

大型商业有限元软件ABAQUS 具有强大的非线性分析功能，且可以便利的对模型的椭圆度、径厚比、材料弹塑性等参数进行局部调整，适合大批量的分析。对于压溃问题的计算，ABAQUS 软件提供了特征值屈曲和非线性屈曲分析两种计算方法。特征值屈曲用于计算理想弹性结构的极限压溃值，相当于弹性压溃分析，但实际中管道的初始椭圆度等缺陷和材料的非线性影响可能会使管道未达到理论的弹性解时就发生压溃失效，所以特征值屈曲一般给出非保守的结果。非线性屈曲分析可以考虑管道的初始椭圆度、材料弹塑性等因素，计算结果更接近实际情况。本文的计算均采用非线性屈曲分析的计算方法。

建立外径210 mm，厚度6 mm 的管道有限元模型，建模过程中引入0.3%的初始椭圆度。管道模型的材料取理想弹塑性材料模型，相关参数见表1。采用三维8 节点实体单元（C3D8I）进行网格的划分，C3D8I 单元位移和应力结果很精确，厚度方向只需要很少的单元就可保持和二次单元相当的精度，本文的计算中壁厚方向的单元数取3 可以在保证计算精度的同时最大程度的节约计算成本。建立实体模型，x、y方向为管道径向方向，z方向为管道轴向方向。设置边界条件，管道两端面的节点限制z方向的位移，只允许在端部平面发生平动；x=0 平面内的节点约束x方向的平动，允许其它方向的平动；同样的y=0 平面内的节点约束y方向的平动，允许其它方向的平动，如图8 所示。接触关系设置为硬接触，防止管道压溃后出现管壁体积相交的不合理现象。管壁外侧施加比理论计算值稍大的外压荷载，并设置相应的加载路径。图2 和图3 为径厚比为35的管道模型的建立过程，类似的分别建立径厚比为10～50 的一系列模型并进行相应的压溃模拟计算。

有限元计算的极限压溃值通过读取端部x=0或y=0 平面内的某一节点的位移随外压变化的曲线得到，当节点位移突然发生变化时可以确定此时的外压荷载为极限压溃值，如图4 所示。通过曲线可以判断管道的极限压溃值为9.939 MPa。同理可得到其他径厚比模型的极限压溃值，如图5 所示。

表1 模型材料参数

图2 模型网格划分

图3 模型边界条件设置

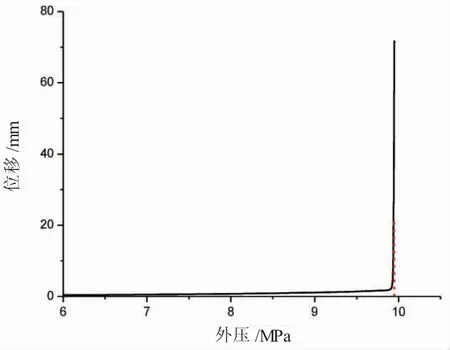
图4 压力—位移曲线

3 压溃实验

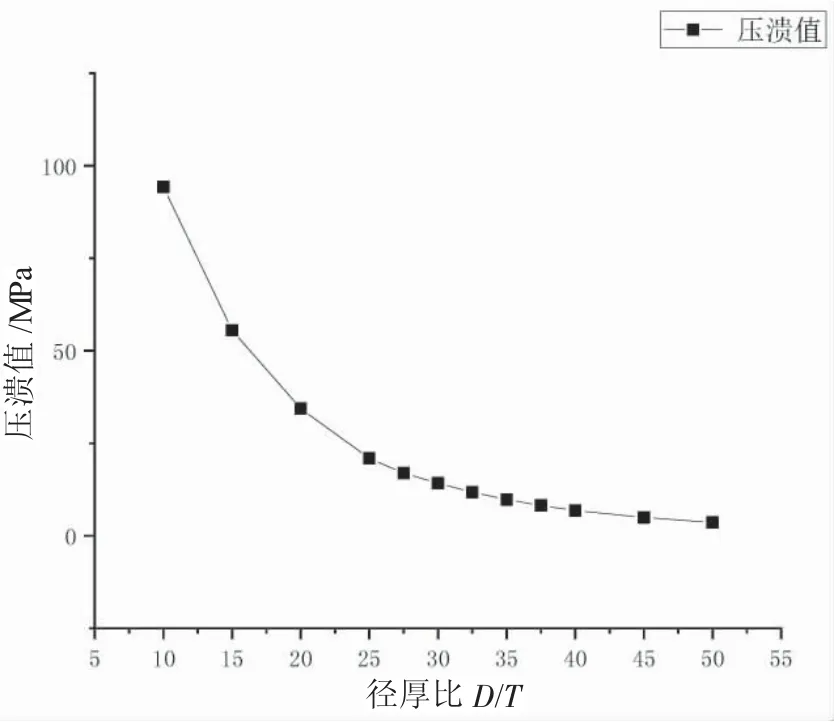
图5 有限元极限压溃值

本节分别进行了无初始椭圆度钢管和挤压出一定椭圆度的钢管的压溃试验。试验中所用的样管是Sch30 系列DN300 的无缝钢管，样管有效长度2.8 m（8.6 倍直径）。由于实验样管的初始椭圆度较小（椭圆度为0.018%）无法使压溃值产生明显变化，因此对样管进行椭圆化处理。钢管径向挤压原理图如图6，模拟安装过程中张紧器的挤压作用，使用压缩实验机WAW-600C 径向挤压出椭圆度。挤压后在钢管挤压位置等间距的取3 个点测量多个方向的直径，并测其椭圆度，测量数据见表2。用厚度仪在钢管两个端面选多个点测厚度，测量数据见表3。取样管的最大椭圆度0.398%和最小厚度8.145 mm为试验样管的基本尺寸。

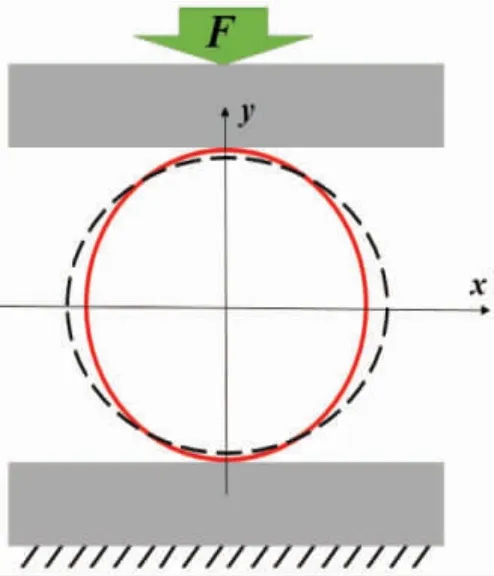
图6 钢管径向挤压原理图

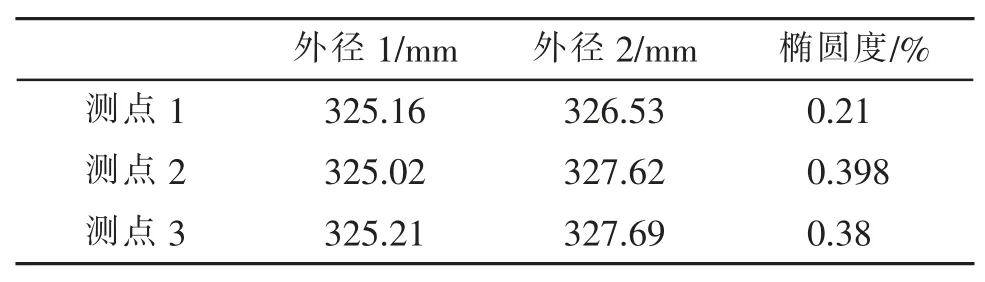
表2 椭圆度测量记录表

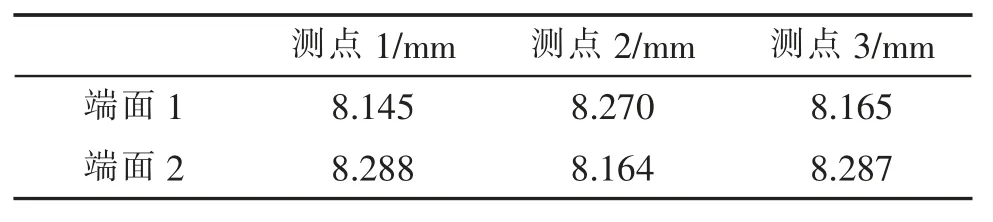
表3 厚度测量记录表

对钢管两端焊接密封后，分别放入压力舱进行实验，如图7 和图8。

图7 端部密封

图8 压力舱

由试验得到，初始椭圆度为0.018%的样管在第355.2 s 发生压溃，压溃值是7.27 MPa；初始椭圆度为0.398%的样管在第326.6 s 时发生压溃，压溃值是6.60 MPa（图9）。试验前后钢管的对比如图10。

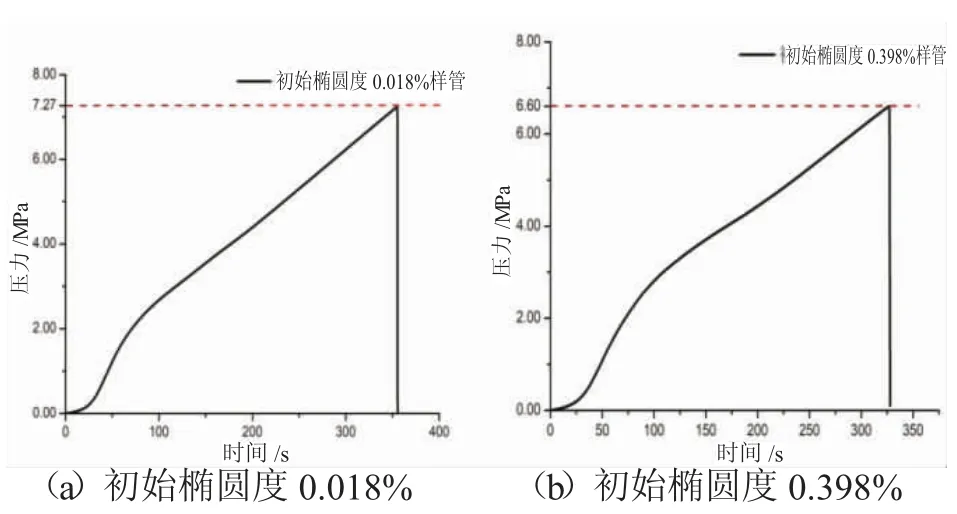
图9 压溃试验压力曲线

图10 试验前后钢管对比

由两组压溃试验的结果分析可知，当样管的初始椭圆度从0.018%增加到0.398%时极限压溃值从7.27 MPa 降低到6.60 MPa，降低了9.21%，由此可得椭圆度对管道的抗压溃性能有显著影响。

4 结果分析与比较

把两组不同初始椭圆度DN300 钢管模型的实验和有限元结果汇总如表4 所示。可以发现有限元的结果均大于实验值，一是误差问题，测量钢管的尺寸中存在误差，测得的椭圆度可能并不是最大初始椭圆度，二是不稳定的实验环境，试验过程中压力泵的加压采用电机驱动，步进式加压。两组钢管的实验值和有限元结果误差较小，结果高度一致，证明本文建立有限元模型是正确的，通过有限元计算可以准确模拟有初始椭圆度钢管的压溃行为，后续可以采用有限元的方式研究考虑椭圆度的钢管压溃问题。

根据弹性压溃理论、塑性压溃理论模型和DNV规范公式分别计算出不同初始椭圆度下的极限压溃值，和有限元模拟计算的结果一起汇总到表5中。极限压溃值对比如图11。

表4 结果汇总

表5 极限压溃值与误差分析

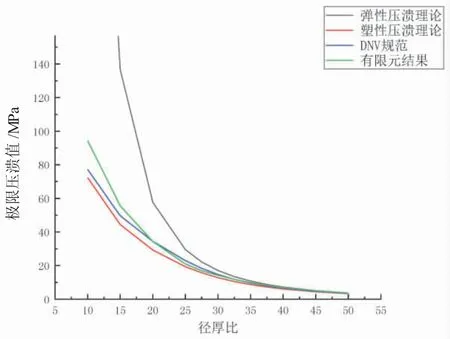
图11 极限压溃值对比图

由表中可以看出弹性压溃理论对小径厚比管道的极限压溃值预测较差，尤其是D/T≤20 时，与有限元结果相比误差超过65%以上，但随着径厚比的增加，弹性压溃理论的计算结果误差逐渐降低，当管道是D/T≥40 的薄壁结构时误差在5.59%左右，能比较准确地预测压溃值。

塑性压溃理论的计算结果均小于有限元模拟计算的结果，偏于保守。在32.5≤D/T≤50 范围内，误差基本稳定在11%左右。

由表4 的数据分析可知：DNV 规范的压溃计算公式在15≤D/T≤50 范围内有较好的适用性，在规范规定的径厚比范围内能准确预测考虑椭圆度的钢管的压溃值，且对超出规定范围的大径厚比钢管的压溃值也能准确预测，是目前适用范围最广的压溃计算理论。

5 结论

本文通过实验和数值结合的方法对现有的公式进行适用性讨论，对海洋管道的设计提供了积极的建议，未来工作将考虑拉伸、弯曲和椭圆度联合作用下对海洋管道的影响，结论如下：（1）弹性压溃理论不能考虑有初始椭圆和材料非线性的影响，仅能准确预测径厚比D/T≥40 的薄壁钢管的极限压溃值；（2）塑性压溃理论预测结果过于保守，均小于有限元结果，这也说明管道压溃时材料并没有完全达到屈服状态;（3）DNV 规范的压溃计算公式在规定范围内能很好的预测考虑椭圆度的钢管的极限压溃值，即使对于超出规范要求范围的径厚比D/T＞45 的情况也能准确预测，是目前适用范围最广的压溃计算理论，可依据DNV 公式进行考虑椭圆度的抗压溃设计；（4）初始椭圆度为0.018%和0.398%的无缝钢管的原型压溃试验结果表明，椭圆度是影响钢管抗压溃性能的重要因素，因此在钢管的抗压溃设计中不能忽略椭圆度的影响。